Trở lại với chủ đề về thống kê, ở phần trước chúng tôi đã giới thiệu đến các bạn các khái niệm về thống kê cũng như lợi ích và ứng dụng của nó, tiếp theo ở phần này, chúng tôi sẽ đề cập đến một mảng kiến thức quan trọng khác đó chính Descriptive statistics (thống kê mô tả) Dành cho những bạn chưa xem qua phần đầu: Tổng quan về Statistics: khái niệm và ứng dụng của thống kê
Những kiến thức cơ bản, quan trọng cần nắm trong Descriptive Statistics
(Lưu ý ở bài viết này chúng tôi sẽ không đề cập đến tóm tắt và trình bày dữ liệu, vì các đồ thị trong bước này chúng tôi sẽ gộp vào trình bày vào bài viết Data visualization sắp tới)
Những thông tin, kiến thức chúng tôi trình bày dưới đây được tổng hợp, tham khảo từ các giáo trình, tài liệu mà chúng tôi đã đề cập ở phần trước khái niệm và ứng dụng của Statistics.
Mẫu và tổng thể:
Tổng thể (population): là tập hợp các đơn vị (hay phần tử) mà chúng ta quan tâm để quan sát, thu thập dữ liệu và tiến hành phân tích, nghiên cứu.
Mẫu (sample): là một tập hợp con bao gồm các đơn vị (hay phần tử) lấy ra từ tổng thể bằng những phương pháp lấy mẫu, mục đích đại diện cho tổng thể nghiên cứu.
Thông thường trong thực tế chúng ta không thể thu thập tất cả các đơn vị trong một tổng thể, hoặc một tổng thể có rất nhiều đơn vị tổng thể khiến cho việc phân tích mất thời gian, tốn kém do đó tại sao thống kê lại đề cao quá trình lấy mẫu, và cung cấp các phương pháp để nhờ vào đó thông qua mẫu lấy được có thể đưa ra các kết luận về tổng thể. Ví dụ xem xét về mức độ liên quan giữa thời gian làm thêm đến kết quả học tập của sinh viên tại một trường đại học, nếu chúng ta thu thập dữ liệu của tất cả sinh viên của trường đại học ấy thì phức tạp và khó khăn, thay vào đó chọn ngẫu nhiên một số lớp sinh viên để nghiên cứu. Một câu nói vui trong thống kê: “Tất cả mọi thứ chúng ta làm trong thống kê đều chỉ dựa vào mẫu nhưng điều chúng ta quan tâm lại là đặc điểm của tổng thể nghiên cứu.”
Lưu ý: mặc dù là kiến thức quan trọng, nhưng trong bài viết này chúng tôi sẽ không đề cập đến phương pháp và quy trình lấy mẫu mà chỉ tập trung vào những kiến thức, công thức toán học trong thống kê mô tả. Mong các bạn thông cảm
Tham số tổng thể và số liệu thống kê:
Tham số tổng thể (aparameter) là một giá trị, thường là một số liệu được dùng để mô tả tổng thể. Một parameter thường được đo lường, tính toán trên các đơn vị trong tổng thể.
Số liệu thống kê (a statistic) là một giá trị, thường là một số liệu được dùng để mô tả một mẫu. Một số liệu thống kê thường được đo lường, tính toán trên các đơn vị trong mẫu.
Dữ liệu, biến, quan sát và thang đo:
Dữ liệu (data) là toàn bộ những thông tin, dữ kiện, các sự thật, các con số,…của các đơn vị (phần tử) trong tổng thể với mục đích thu thập, phân tích, tóm tắt, nghiên cứu…. về một hiện tượng, vấn đề nào đó.
Quan sát (observation) là tập hợp các dữ liệu của 1 đơn vị tổng thể thu thập được thể hiện dưới các thang đo (measurement) khác nhau. Ví dụ học sinh Nguyễn Văn A (1 đơn vị nghiên cứu trong tổng thể) có tuổi: 18, quê quán: tp Hồ Chí Minh, điểm trung bình: 8.0, học lực: giỏi, v.v khi tất cả các thông tin, dữ liệu (các chỗ gạch chân) này đều có thang đo riêng, và thể hiện trên một dòng, thì dòng này gọi là một quan sát.
Biến (variable) là khái niệm dùng để chỉ các đặc điểm của đơn vị (phần tử) trong tổng thể nghiên cứu. Nói cách khác biến là một đặc tính biểu hiện giá trị khác nhau cho các đơn vị tổng thể khác nhau.
Biến (hay dữ liệu) thường có 2 dạng chính là định tính (qualitative/categorical variable), định lượng (quantitative/numerical variable).
Biến định tính hay biến phân loại là biến phản ánh tính chất, hay loại hình, không có biểu hiện trực tiếp bằng con số. Ví dụ giới tính, nghề nghiệp, tình trạng hôn nhân, dân tộc, tôn giáo, học thức, v.v Với biến định tính chúng ta có thể đếm số quan sát cho từng loại, và tính % cho mỗi loại trong tổng thể. Ví dụ số người độc thân đếm được là 350, tổng số quan sát là 1000 vậy chiếm 35%.
Có hai dạng Nominal (định danh), và Ordinal (thứ bậc)
Biến định lượng là biến biểu hiện trực tiếp bằng con số ví dụ tuổi, chiều cao, trọng lượng, năng suất làm việc của công nhân, số dư trong tài khoản ngân hàng, thời gian sử dụng PIN điện thoại, v.v. Biến định lượng được chia làm 2 loại biến định lượng rời rạc (discrete) và biến định lượng liên tục (continuous)
Biến định lượng rời rạc (discrete variable) là biến mà giá trị của nó có thể vô hạn, hữu hạn và có thể đếm được. Một biến rời rạc bao gồm các loại riêng biệt, không thể chia tách, không có giá trị có thể tồn tại giữa hai giá trị kế nhau. Ví dụ, số trẻ em trong một gia đình hoặc số học sinh tham gia lớp học. Nếu bạn quan sát lớp học từ ngày này sang ngày khác, bạn có thể đếm 20 sinh viên một ngày và 21 sinh viên vào ngày hôm sau.
Tuy nhiên, không thể bao giờ quan sát một giá trị trong khoảng từ 20 đến 21 (tức không thể nào có 20.5 sinh viên). Một biến rời rạc cũng có thể bao gồm các quan sát khác nhau về chất (định tính). Ví dụ, một người có thể được phân loại theo thứ tự sinh (sinh trước hoặc sinh sau), theo nghề nghiệp (y tá, giáo viên, luật sư, v.v.) và sinh viên đại học có thể được phân loại theo chuyên ngành học thuật (nghệ thuật, sinh học, hóa học, v.v. .). Trong mỗi trường hợp, các biến đó là rời rạc vì nó bao gồm các loại riêng biệt, không thể chia tách.
Biến định lượng liên tục (continuous variable) là biến mà các giá trị của nó có thể chia tách hoặc nói cách khác các giá trị của nó có thể lấp đầy một trục số. Ví dụ trọng lượng, chiều cao của một người,.v.v. Biến định lượng liên tục thường có giá trị vô hạn, hay có vô số giá trị có thể nằm giữa bất kỳ hai giá trị quan sát (ví dụ giữa 0 và 1 có 0.1516, 0.98999), không thể quan sát, không thể đếm được.
Ngoài biến đinh tính và biến định lượng ta có thêm một loại biến khác gọi là biến nhị phân (binary variable).
Biến nhị phân là trường hợp mà các biến định tính và định lượng (hiếm gặp) chỉ có 2 giá trị, 2 biểu hiện không trùng nhau của một đơn vị, nếu đơn vị không có giá trị này, thì phải chứa giá trị còn lại của biến thay phiên. Ví dụ hỏi sinh viên nào đã tham gia chương trình “Mùa hè xanh” thì sinh viên chỉ có thể trả lời “có” hoặc “không”; khách hàng đã rời bỏ dịch vụ của công ty hay chưa “đã rời bỏ” hoặc “chưa rời bỏ”. Trong trường hợp một biến của một đối tượng nghiên cứu có nhiều giá trị và vô số biểu hiện thì chúng ta có thể chuyển thành biến thay phiên ví dụ thành phần kinh tế có thể chia thành 2 phần là thành phần kinh tế nhà nước và ngoài nhà nước thay vì là 5 (kinh tế nhà nước, kinh tế tập thể, kinh tế tư nhân (cá thể, tiểu chủ, tư bản tư nhân), kinh tế tư bản nhà nước, kinh tế có vốn đầu tư nước ngoài) để tránh sự phức tạp.
Biến nhị phân có 2 dạng: Symmetric (đối xứng) và Asymmetric (không đối xứng)
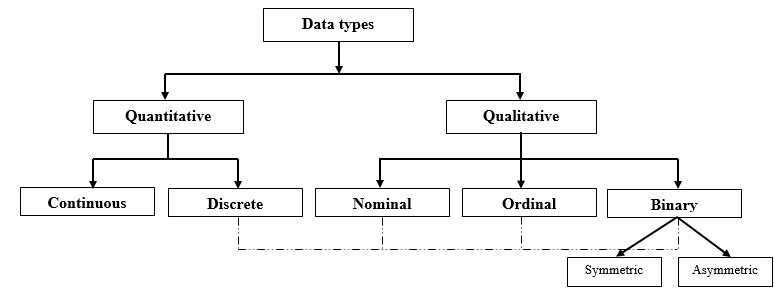
Những nét đứt khúc ở đồ thị trên là do trong một số tài liệu khác, các biến phân loại theo Nominal, Ordinal, hay Binary được xem là biến rời rạc Discrete vì như chúng tôi trình bày biến Discrete có thể là các biến định tính, các bạn có thể xem lại ở trên (mong các bạn lưu ý thêm).
Thang đo
Scales of Measurement (thang đo) lượng hóa hiện tượng nghiên cứu xác định lượng thông tin có trong dữ liệu, phân loại dữ liệu, chỉ ra các phân tích thống kê và là cơ sở để tóm tắt, trình bày dữ liệu phù hợp nhất.
Nominal scale (thang đo định danh) dùng cho biến định tính, hay biến danh nghĩa, tức các giá trị, dữ liệu được biểu hiện dưới mã số, nhãn hoặc tên, không có sắp xếp theo trật tự, không có quan hệ hơn kém, chỉ được dùng để phân loại các đối tượng nghiên cứu với nhau, và đếm tần số xuất hiện của các biểu hiện. Ví dụ tình trạng hôn nhân của bạn: 1. Độc thân 2. Có gia đình 3. Đã ly dị 4. Trường hợp khác.
Ordinal scale (thang đo thứ bậc) được sử dụng cho biến định tính, và có trường hợp cho biến định lượng, trong thang đo này, giá trị hay biểu hiện của biến có mối quan hệ hơn kém, có thứ bậc, sự chênh lệch, hoặc khoảng cách giữa 2 giá trị hay biểu hiện không nhất thiết bằng nhau Ví dụ thu nhập trung bình của bạn là bao nhiêu mỗi tháng?
- < 3 triệu VND 2. Từ 3 – 5 triệu VND 3. Từ 5 – 8 triệu VND 4. > 8 triệu VND
Interval scale (thang đo khoảng) được dùng cho biến định lượng và trường hợp cả biến định tính, thang đo khoảng chính là thang đo thứ bậc có khoảng cách đều nhau hoặc khoảng cách được xác định rõ ràng, mang ý nghĩa phân tích. Ví dụ nhiệt độ 290C – 330C khoảng cách 40C, 350C – 390C cũng chênh lệch 40C.
Ratio scale (thang đo tỷ lệ) có đầy đủ tính chất của thang đo khoảng, tỷ lệ giữa 2 giá trị thu thập có ý nghĩa, có thể áp dụng phép toán cộng trừ, và số 0 trong thang đo này có giá trị thật tức có ý nghĩa thật sự. Ví dụ bạn có 50000 VND, bạn dùng hết và còn 0 đồng, nghĩa là bạn không còn gì hết. Tiền tệ có trị số 0 thật nên nó là thang đo tỷ lệ. Khác với nhiệt độ là thang đo khoảng, ví dụ chúng ta không thể nói 00C nghĩa là không có gì, mà 00C tức là rất lạnh, lạnh hơn 100C, 200C,…
Lưu ý các thang đo cấp cao hơn sẽ bao hàm tính chất của các thang đo cấp nhỏ hơn.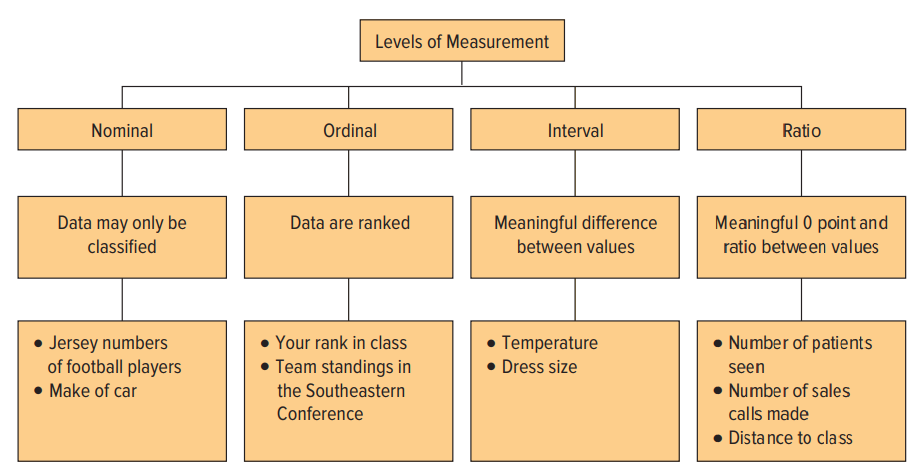
Nguồn hình: “Basic Statistics for Business and Economics” (9th Edition 2019) của nhà xuất bản Mc Graw Hill
Các đặc trưng đo lường mức độ, khuynh hướng tập trung của dữ liệu
Đo lường khuynh hướng tập trung (Measures of Central tendency) là xác định các chỉ tiêu biểu hiện mức độ đại diện của một biến định lượng nào đó của một tổng thể bao gồm nhiều đơn vị cùng loại.
- Mean (số trung bình cộng):
Giá trị trung bình là tổng giá trị của các quan sát chia cho số lượng quan sát, được hiểu là điểm cân bằng. Mean là sự san bằng bù trừ chênh lệch tất cả các giá trị trong tập dữ liệu, là đại diện cho độ tập trung của dữ liệu. Nhược điểm của mean là nhạy cảm với các giá trị đột biến, giá trị ngoại lệ. Ví dụ trung bình của (3+4+5+6+7+8) = 5.5, trung bình của (3+4+5+6+7+30) = 9.16 Công thức:
Trung bình của tổng thể:
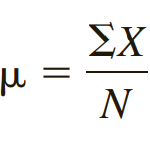
Trung bình của mẫu:
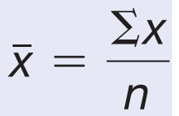
N: là tổng số đơn vị, quan sát trong tổng thể
n: là tổng đơn vị, quan sát trong mẫu rút ra từ tổng thể.
∑X: là tổng giá trị của các đơn vị trong tổng thể
∑x: là tổng giá trị của các đơn vị trong mẫu
- Median (trung vị)
Median (Me) là giá trị đứng ở vị trí trung tâm, ở vị trí giữa trong dãy số sắp xếp từ bé đến lớn. Trung vị sẽ chia dãy số thành 2 phần mỗi phần có số quan sát, hay số đơn vị bằng nhau. Trường hợp tổng số quan sát là số lẻ, thì trung vị là giá trị đứng ở vị trí thứ (n+1)/2 còn trường hợp tổng số quan sát là số lẻ thì median sẽ là trung bình cộng (n/2) và (n+2)/2. Trung vị có ưu điểm hơn Mean vì thể hiện mức độ tập trung chính xác hơn và không bị ảnh hưởng bởi các giá trị đột biến hay ngoại lệ. Ví dụ: (dãy số n = 9) 2000; 2200; 2250; 2300; 2400; 2500; 2700; 3000; 3300, Me ở vị trí (9+1)/2= 5 là 2400.
Ví dụ (dãy số n=10) 2000; 2200; 2250; 2300; 2400; 2500; 2700; 3000; 3300; 3400, Me là giá trị trung bình của 2 giá trị ở vị trí (10/2) = 5 và (10+2)/2 = 6, tức bằng (2400 + 2500)/2 = 2450 Mode (Mo) là chỉ tiêu thể hiện một giá trị, hay một biểu hiện của một biến được lặp lại nhiều nhất trong dãy số, hay tập dữ liệu.
- Mode (Mốt)
Mode tính toán dựa trên tần số là số lần lặp lại của biểu hiện hay giá trị của biến. Mốt không chịu ảnh hưởng bởi các giá trị ngoại lệ, đột biến nhưng lại không nhạy cảm với sự biến thiên của dãy số. Mốt phù hợp cho các trường hợp nghiên cứu thị trường ví dụ như khách hàng ưa chuộng mặt hàng nào nhất trong dòng sản phẩm A. Ví dụ số sinh viên có điểm số là 5 điểm: 20 sinh viên, tiếp đến với điểm số là 6 thì có 15 sinh viên, là 7 thì có 10 sinh viên, là 8 thì có 30 sinh viên, là 9 thì có 8 sinh viên, là 10 thì có 1 sinh viên, vậy Mo = 8 (không lấy tần số, hay số sinh viên làm Mo)
Lưu ý ở phần này và các phần sau, là những công thức chúng tôi giới thiệu chỉ là công thức chung, trình bày bản chất của các chỉ số, còn rất nhiều trường hợp, nhiều công thức khác các bạn có thể tìm kiếm, tra cứu trên mạng và tham khảo thêm ở những tài liệu khác chi tiết hơn. Mong các bạn thông cảm.
Như vậy chúng ta đã biết về các thang đo dùng cho dữ liệu nào, chúng ta cùng xem qua mối quan hệ giữa các chỉ số đo lường độ tập trung với các thang đo.
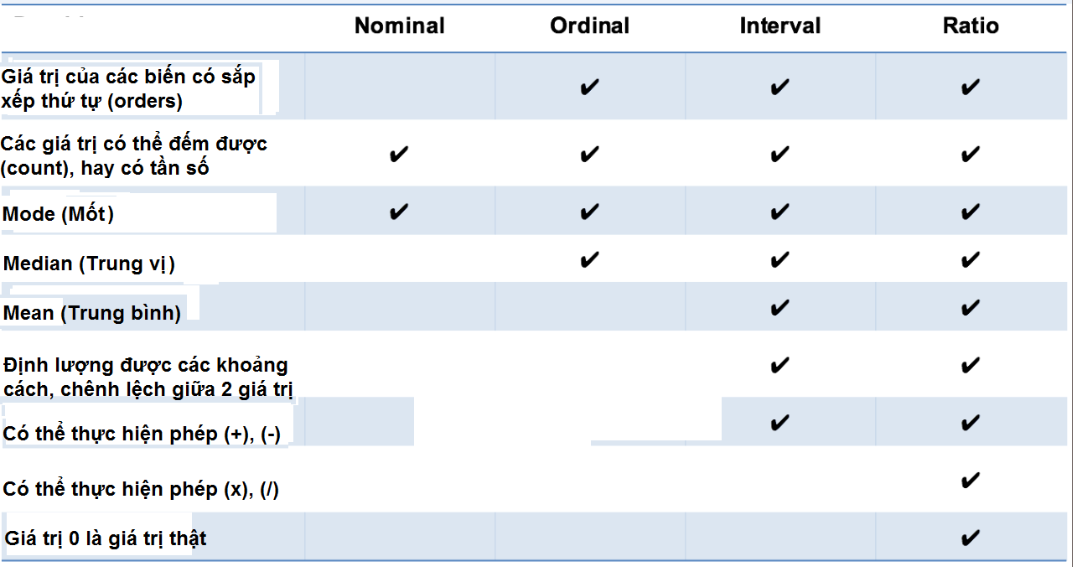
Các đặc trưng đo lường khuynh hướng phân tán của dữ liệu
Chúng ta đã biết qua các chỉ số mô tả khuynh hướng tập trung của dữ liệu, tức chỉ mới biết về những giá trị đại diện của các biến trong dữ liệu hay nói cách khác mới biết được dữ liệu tập trung nói về cái gì, nhưng chúng ta chưa có thông tin về mức độ thay đổi, hay chênh lệch giữa các giá trị của các biến trong dữ liệu, nói cách khác là độ biến thiên, hay phân tán của dữ liệu.
Các chỉ số thể hiện độ phân tán đóng góp rất nhiều ở các phương pháp thống kê suy nhiễn từ ước lượng, kiểm định, phân tích nguyên nhân – kết quả (ANOVA), hồi quy tương quan (quan hệ nhân – quả giữa các đối tượng nghiên cứu), v.v Các bạn cùng xem qua ví dụ biểu đồ dưới đây lấy từ “Essentials of Statistics For The Behavioral Sciences” (9th edition) của Cengage Learning. Ở biểu đồ (a) giá trị 70 inches chính là trung bình của dãy số liệu về chiều cao của người trung niên tương tự ở biểu đồ (b) là 170 pounds, trung bình của dãy số liệu về cân nặng. Chúng ta thấy các số liệu về chiều cao phân tán ít hơn, so với số liệu về cân nặng. Để tìm ra mức độ phân tán chúng ta cần phải biết về các chỉ số đo lường khuynh hướng biến thiên (Measures of Dispersion / Variability)

Nguồn hình “Essentials of Statistics For The Behavioral Sciences” (9th edition) của Cengage Learning
- Range (khoảng biến thiên)
Là khoảng cách giữa giá trị lớn nhất (Max) và giá trị nhỏ nhất (Min) của dãy số. Range càng nhỏ thì tổng thể càng đồng đều, Mean sẽ có tính đại diện cao hơn và ngược lại nếu Range cao thì tổng thể càng phân tán, tính đại diện của Mean sẽ thấp hơn. Range là thước đo đơn giản nhất nhưng cũng có nhược điểm lớn nhất là chỉ chú ý đến Min và Max chưa phản ánh đầy đủ mức độ biến thiên của các quan sát, đặc biệt Range rất nhạy cảm khi có giá trị ngoại lệ, đột biến.
Ví dụ có 2 tổ sản xuất với năng suất làm việc (ví dụ m vải) như sau: Tổ 1: 30, 36, 28, 39, 40, 45 có Range = 45 – 28 = 17 Tổ 2: 25, 34, 42, 33, 44, 48 có Range = 48 – 25 = 23
Vậy tổ 2 có năng suất lao động biến thiên nhiều hơn tổ 1.
- Percentiles (Phân vị), Quartiles (Tứ phân vị), Interquartile Range (Độ trải giữa)
Phân vị thứ p (p nằm từ 0 đến 100) trong một dãy số sắp xếp theo thứ tự tăng dần là một giá trị chia dãy số thành 2 phần với một phần gồm p% số đơn vị có giá trị nhỏ hơn hoặc bẳng phân vị thứ p, phần còn lại có (100 – p) % số đơn vị có giá trị bằng hoặc lớn hơn phân vị thứ p. Tứ phân vị chia dãy số thành 4 phần, mỗi phần có số quan sát, số đơn vị bằng nhau.
Ví dụ trung vị chính là phận vị thứ 2 kí hiệu Q2 tức có 50% số quan sát có giá trị lớn hơn Q2 và 50% số quan sát có giá trị nhỏ hơn Q2. Tứ phân vị bao gồm Q1 (tứ phân vị thứ 1, ứng với phân vị thứ 25), Q2 (trung vị, ứng với phân vị thứ 50), và Q3 (tứ phân vị thứ 3, ứng với phân vị thứ 75). Tứ phân vị được dùng để tính toán độ trải giữa, là chênh lệch giữa Q1 và Q3, chỉ số đo lường khuynh hướng phân tán của dữ liệu. Công thức của phân vị vị trí i:
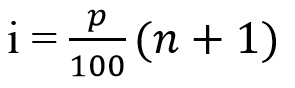
Q1 trong tứ phân vị ứng với p = 25 vậy nằm ở vị trí 25%*(n + 1) của dãy số với n là tổng các quan sát trong dãy số, Q3 ứng với p = 75, nằm ở vị trí 75%*(n + 1).
Như vậy chúng ta sẽ tìm được độ trải giữa, độ trải giữa càng lớn thì dãy số phân tán nhiều và ngược lại.
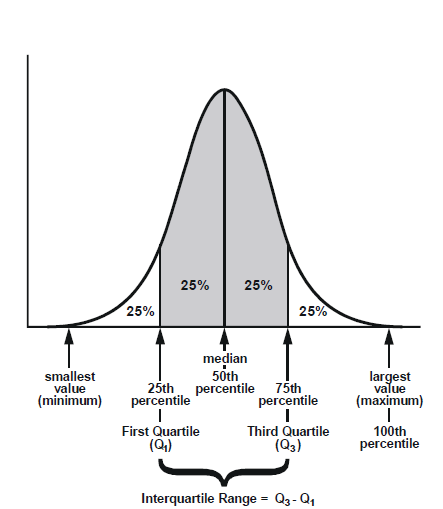
Hình minh họa về tứ phân vị và độ trải giữa (nguồn hình: satmasterkey.com)
- Mean absolute deviation (MAD – độ lệch tuyệt đối trung bình)
Là trung bình cộng của độ lệch tuyệt đối giữa các giá trị của từng quan sát trong dãy số và trung bình cộng của dãy số (Mean). Nếu độ lệch tuyệt đối trung bình càng nhỏ, thì tổng thể sẽ càng đồng đều, tính chất đại diện của Mean sẽ cao hơn. Mean absolute deviation xét đến tất cả các giá trị, các biến trong dãy số nên đo lường khuynh hướng phân tán tốt hơn Range và độ trải giữa.
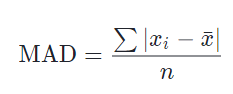
Công thức trên tính cho mẫu, còn chon tổng thể thì chúng ta thay trung bình tổng thể vào công thức.
- Variance (phương sai) và Standard Variance (độ lệch chuẩn)
Phương sai là trung bình cộng của bình phương các độ lệch giữa các giá trị của từng quan sát và số trung bình cộng (Mean) của dãy số. Độ lệch chuẩn chính là căn bậc 2 của phương sai. Phương sai lớn phản ánh khuynh hướng phân tán nhiều, và độ biến thiên cao của dữ liệu, độ lệch chuẩn đại diện cho một giá trị trung bình, là chênh lệch giữa giá trị của mỗi quan sát so với trung bình cộng của dãy số, do đó cũng thể hiện được độ biến thiên, độ lệch chuẩn càng cao thì dãy số phân tán nhiều và ngược lại. Phương sai tổng thể nghiên cứu:
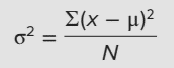
Phương sai của mẫu hiệu chỉnh (thường được dùng phổ biến trong thống kê suy diễn)
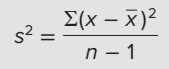
Còn độ lệch chuẩn thì các bạn cứ lấy căn bậc 2 của 2 công thức trên.
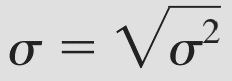
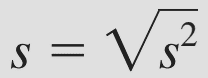
Phương sai và độ lệch chuẩn được sử dụng hỗ trợ trong các phương pháp ước lượng, kiểm định, ANOVA, và phân tích hồi quy.
- Z-score (chuẩn hóa dữ liệu)
Z-score cho chúng ta biết một giá trị của một quan sát bất kỳ trong dữ liệu lệch khỏi trung bình cộng của dãy số bao nhiều lần độ lệch chuẩn. Gọi Z-score là một phương pháp chuẩn hóa dữ liệu vì nó được sử dụng để biến đổi những dữ liệu định lượng với những đơn vị đo khác nhau thành một thang đo chuẩn. Z-score được dùng để chuẩn hóa dữ liệu giả định cho tổng thể có phân phối chuẩn ở thống kê suy diễn.
Hệ số chuẩn hóa Z cho dữ liệu mẫu:
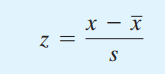
Hệ số chuẩn hóa Z cho dữ liệu tổng thể:
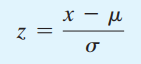
Ví dụ để các bạn dễ hiểu: bài kiểm tra năng lực của một nhóm nhân viên M khi sử dụng phương pháp kiểm tra A là 1200 điểm, cùng với nhiều nhóm nhân viên khác cùng thực hiện phương pháp kiểm tra A chúng ta có được trung bình là 1000 điểm, độ lệch chuẩn là 300. Tương tự một nhóm nhân viên N khác khi được cho làm bài kiểm tra ở phương pháp kiểm tra B thì được 100 điểm, trung bình của phương pháp này là 90 điểm, độ lệch chuẩn là 20. Dựa trên công thức chúng ta sẽ có ZM(A) = 0.67 còn ZN(B) = 0.5. Mặc dù áp dụng 2 phương pháp kiểm tra cho 2 nhóm nhân viên M và N nhưng qua hệ số Z ta thấy được điểm của nhóm M cao hơn trung bình 0.67 lần độ lệch chuẩn, còn nhóm M chỉ có 0.5 vậy kết luận nhóm M hoàn thành bài kiểm tra năng lực tốt hơn.
- Một số quy tắc phân phối, và phương pháp khảo sát hình dạng của dãy số
Quy tắc thực nghiệm (Empirical Rule/Rule of Thumb)
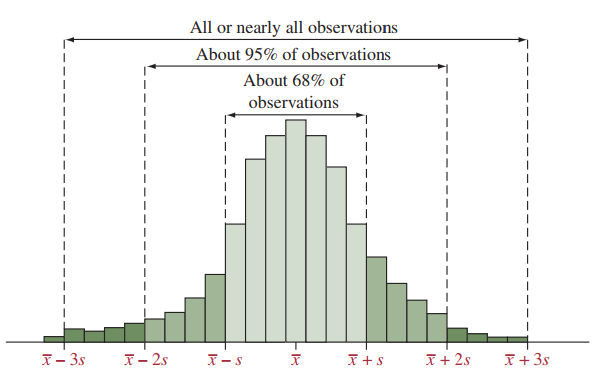
Nguồn hình: “Statistics: The Art and Science of Learning from Data” (4th Global Edition 2018) của Pearson.

Quy tắc Tchebychev (Tchebychev’s Rule)

Phương pháp Skewness
Phục vụ xác định độ nghiên của phân phối.
Nếu giá trị Skewness > 0 (positively skewed) thì đồ thị phân phối lệch phải (tức nghiên về phía phải), Skewness < 0 (negatively skewed) thì đồ thị phân phối lệch trái (tức nghiên về phía trái), Skewness = 0, với Skewness có công thức như sau:
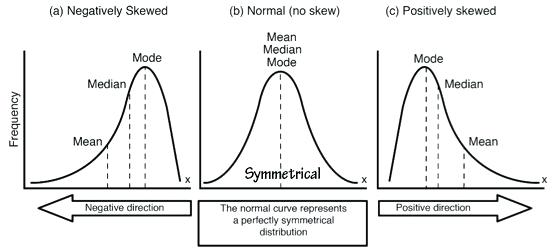
Hình minh họa về phân phối theo Skewness
Biểu đồ hộp và râu (Box-plot): biểu đồ thể hiện 5 giá trị của tập dữ liệu: giá trị bé nhất, tứ phân vị thứ nhất (Q1), trung vị hay tứ phân vị thứ 2 (Q2), tứ phân vị thứ 3 (Q3), giá trị lớn nhất, và những trị số bất thường. Biểu đồ hộp râu giúp mô tả cụ thể khuynh hướng phân tán của dữ liệu, bên cạnh đó biểu đồ hộp râu cũng giúp xác định các giá trị ngoại lệ gọi là outlier. Do nếu tập dữ liệu có giá trị ngoại lệ thì chiều dài tối đa của 2 râu tính từ mỗi cạnh hộp sẽ được xác định bằng 1.5 lần độ trải giữa, khi ấy các giá trị ngoại lệ sẽ nằm ngoài giới hạn của 2 râu được thể hiện bằng dấu sao, hoặc dấm chấm
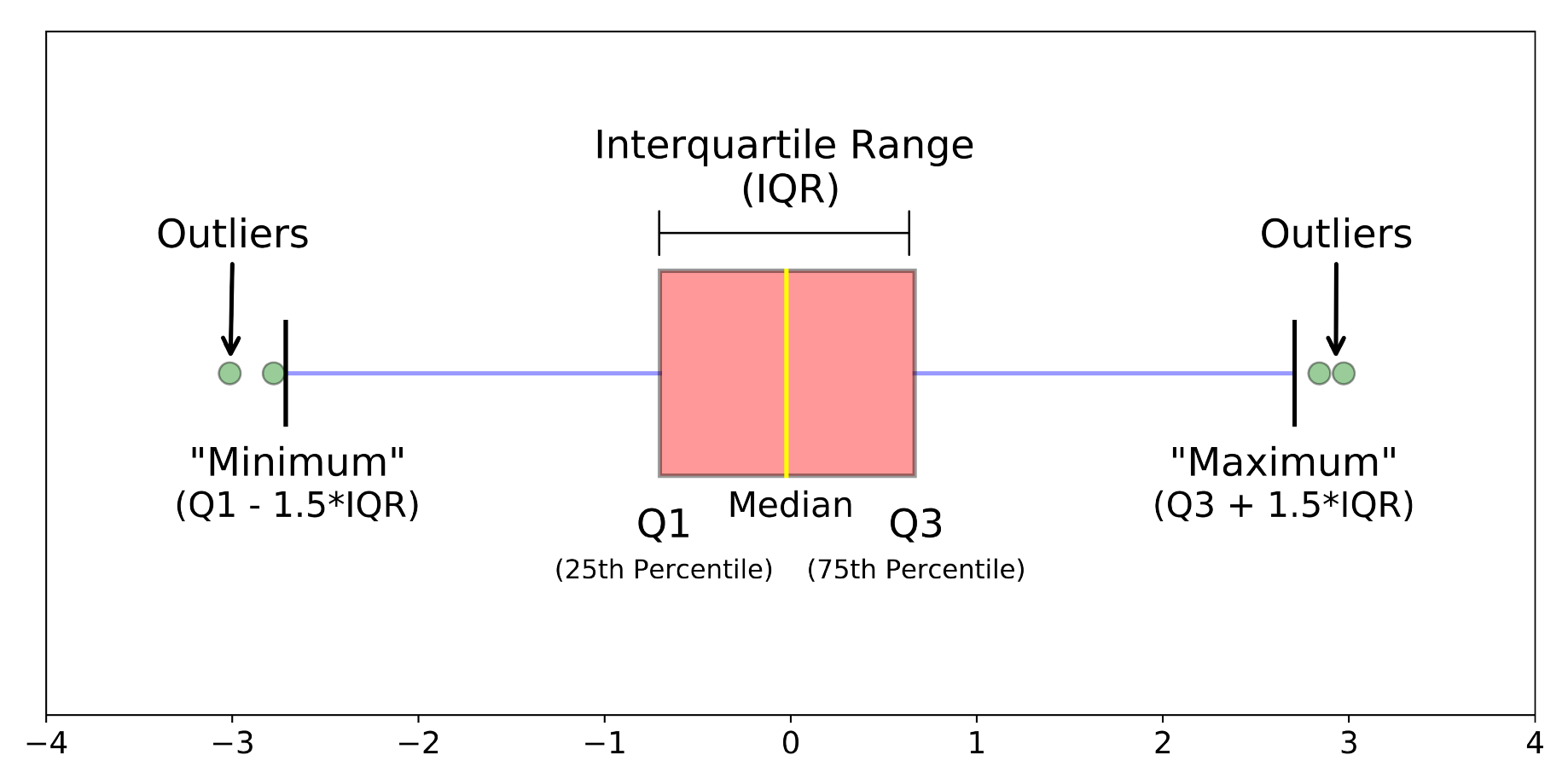
Hình ảnh minh họa biểu đồ hộp râu (nguồn hình: towardsdatascience.com )
Đến đây là kết thúc bài viết về Tổng quan về Statistics: thống kê mô tả. Bài viết sắp tới, như đã nói ở trên, chúng tôi sẽ trình bày về Data visualization (trực quan hóa dữ liệu) bao bồm cả phương pháp tóm tắt, trình bày dữ liệu trong thống kê mô tả. Mong các bạn tiếp tục theo dõi và ủng hộ BigDataUni.
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English