Trở lại với chủ đề Association rules – khai phá luật kết hợp, thì ở bài viết trước, ở phần 1 chúng ta đã cùng nhau tìm hiểu phương pháp Association rules là gì, ý nghĩa và ứng dụng của nó trong lĩnh vực kinh tế, y tế và một số lĩnh vực khác, đặc biệt chúng ta đã tìm hiểu qua cách vận hành của quá trình khai phá luật kết hợp, và các chỉ tiêu cơ bản chọn lựa, đánh giá những luật kết hợp tìm được như Support, Confidence và Lift.
Tiếp tục với phần 2 BigDataUni lần nữa sẽ nói về các bước thực hiện phân tích luật kết hợp, và quan trọng nhất là trình bày về thuật toán phổ biến nhất được sử dụng để khai phá Association rules là Apriori.
Dành cho các bạn chưa xem bài viết trước:
Tổng quan về Association rules (P.1)

Như vậy, các bạn đã được làm quen với Association rules là gì và các tiêu chí đánh giá quan trọng của nó. Trước khi vào nội dung chính phần 2, BigDataUni sẽ điểm lại một vài ý quan trọng ở bài viết trước để các bạn tiện theo dõi.
Gọi trên là tập dữ liệu D, với T = {T1, T2, T3,…TN} là tập các giao dịch có mã số, I = {I1, I2, I3… IN} là tập các sản phẩm đã bán. Với mỗi giao dịch Ti sẽ chứa một tập con các sản phẩm lấy ra từ tập I. Một tập hợp bao gồm giữa 0, 1 hoặc hơn 1 sản phẩm được gọi là “Itemset” – tập phần tử.
Nếu một itemset chứa k các phần tử có thể gọi k-itemset ví dụ 2-itemset thì itemset có chứa 2 phần tử.
Itemset A = {…, …. }, và itemset B = {…, ….}. Chúng ta sẽ xem xét luật kết hợp nếu A được mua, thì B cũng được mua. Với A là Antecedent và B là Consequent, có chứa các tập con nằm trong I. A và B đối lập nhau. A ∩ B = Ø
Support là tỷ lệ xuất hiện các giao dịch có chứa cả A và B trong tập dữ liệu D.
Support = P(A ∩ B) = (Số giao dịch có chứa A và B)/ Tổng các giao dịch
Confidence là thước đo độ chính xác của luật kết hợp tìm được, tính bằng cách tìm tỷ lệ trong số các giao dịch có chứa itemset A trong tập giao dịch D thì có bao nhiêu giao dịch chứa luôn B
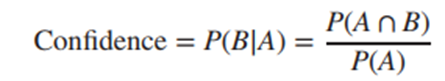
Các luật kết hợp “mạnh” sẽ phải đáp ứng hoặc vượt qua các tiêu chí nhất định hay các yêu cầu được đặt ra, hay còn gọi Threshold, có Support đạt yêu cầu hoặc cao hơn, hay Confidence cao và hoặc là cả hai
Do tùy vào trường hợp, mục đích kinh doanh, và bối cảnh nghiên cứu nên các giá trị tối thiểu của Support và Confidence sẽ khác biệt, nên không có một quy tắc chuẩn.
Lift là tỷ lệ giữa (tỷ lệ các giao dịch có itemset A và B trên tổng các giao dịch chỉ có itemset A) – Confidence trên (tỷ lệ các giao dịch chỉ có itemset B trước đó) Lift gần đến 1 thường chỉ ra luật kết hợp vừa tìm không có ý nghĩa quan tâm và ngược lại.
Công thức tham khảo xác định tổng số luật kết hợp
Các bạn có thể thấy để đánh giá một luật kết hợp chúng ta cần tính đến 2 hoặc 3 chỉ tiêu đánh giá, việc tính toán sẽ rất phức tạp, do số lượng các luật kết hợp trong một tập dữ liệu có thể là rất nhiều, tăng lên theo cấp số nhân nếu lượng dữ liệu tăng lên. Theo tài liệu “Introduction to Data mining” của Pang-Ning Tan, Michael Steinbach và Vipin Kumar thì tổng số Association rules trong một tập dữ liệu có số d item là:
R = 3d – 2d+1 + 1
Chúng ta tạm thời sử dụng các ví dụ đơn giản để hiểu qua trước các công thức trình bày trong bài viết này.
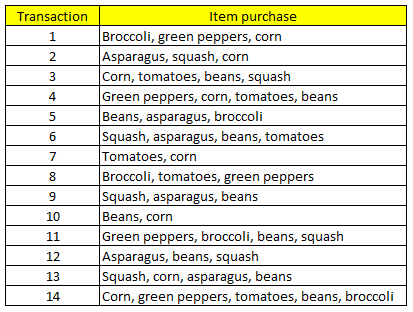
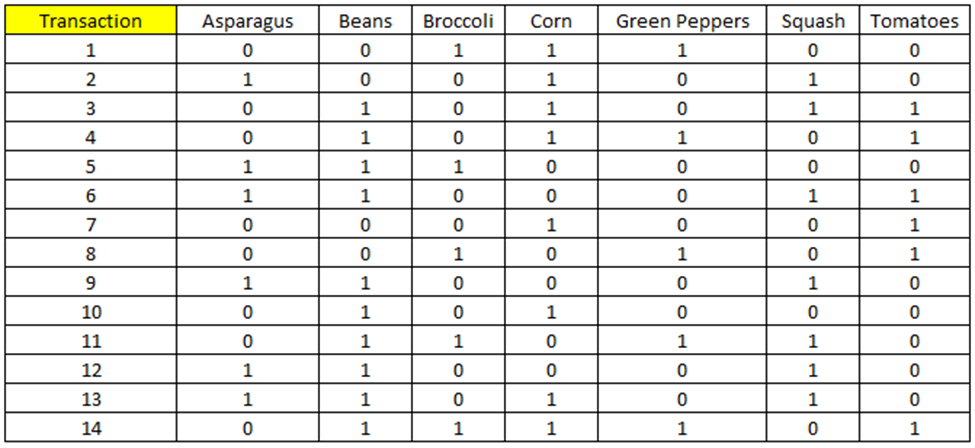
Theo ví dụ được tham khảo từ tài liệu Data mining & Predictive analytics của tác giả Daniel T. Larose, thì có tất cả 7 item, 7 sản phẩm có thể tạo thành các luật kết hợp.
R = 37 – 27+1 + 1 = 1932 luật kết hợp có thể khai phá từ mẫu dữ liệu.
Với 2d – 1 là tổng số itemset (không bao gồm cả itemset rỗng)
Tập dữ liệu trong thực tế của một cửa hàng bán lẻ thông thường thì số item sẽ lớn hơn 7 rất nhiều do có nhiều sản phẩm được bán, nên tổng số association rules cũng như itemset thường không được chú ý đến vì quá nhiều.
Cách tính R trên đã được các chuyên gia xây dựng dựa trên những công thức toán học đã được kiểm chứng nên các bạn có thể áp dụng không cần lo lắng về độ chính xác. Phương pháp các chuyên gia thực hiện chính là đầu tiên xác định tất cả số các itemsets có thể hình thành, sẽ tạm đóng vai là Antecedent (IF), sau đó với mỗi itemset có chứa k item thì tìm tất cả d – k các item có thể kết hợp được, và những d – k item này được gọi là Consequent (THEN).
Như vậy, hướng tiếp cận đơn giản, và được cho cồng kềnh để khai phá luật kết hợp có thể nói gọn trong 3 bước:
- Xác định tất cả các luật kết hợp có thể có
- Tính toán Support, Confidence (hay cả Lift) cho mỗi luật kết hợp
- Loạt bỏ các luật kết hợp không đạt yêu cầu về mức tối thiểu Support và Confidence
Tuy nhiên như đã nói, nguồn dữ liệu ở bối cảnh hiện nay mà một công ty có thể thu thập là rất nhiều và rất phức tạp, nhờ vào sự phát triển của công nghệ, nên hướng tiếp cận trên sẽ tốn rất nhiều chi phí, thời gian tính toán.
Một phương pháp khác khắc phục một phần của hướng tiếp cận trên:
- Tìm những itemset có tần suất xuất hiện nhiều trong tập dữ liệu, hay đạt yêu cầu Frequency > n là một số tối thiểu nào đó, nói cách khác là đáp ứng minimum Support
- Đối với mỗi itemset đạt yêu cầu frequency tìm những luật kết hợp mà ở đó có tỷ lệ Confidence cao, hoặc vượt qua ngưỡng Confidence được đặt ra.
Phương pháp này được coi là tiêu chuẩn và sử dụng phổ biến trong khai phá luật kết hợp, có ưu điểm là xác định trước các itemset xuất hiện thường xuyên trong tập dữ liệu, còn hướng tiếp cận ban đầu liệt kê hết các association rules rồi tính support, confidence trong khi chúng ta vẫn có thể loại trừ trước các itemset ít gặp rồi đi tìm những association rules.
Nhưng việc tính toán chỉ nhẹ đi một phần ở bước thứ 2 mà thôi, tức ở bước xác định rules tối ưu, còn ở bước 1, khi tìm frequency sẽ khá phức tạp.
Ví dụ đối với mỗi itemset chỉ có 1 item, thì chúng ta chỉ việc đếm trong tập dữ liệu thì có bao nhiêu giao dịch chứa item mà mình đang xét đến, hình thức giống thống kê thông thường. Sự phức tạp tăng lên khi tính frequency cho itemset có trên 1 item nếu số d các item riêng biệt ban đầu là khá nhiều, tổng itemset sẽ rất lớn. Lúc này thuật toán Apriori sẽ hỗ trợ giải quyết vấn đề mà phương pháp này gặp phải.
Xác định các itemset xuất hiện phổ biến (frequent)
Hướng tiếp cận khai phá luật kết hợp phù hợp nhất như đã nói ở trên bao gồm 2 bước, với bước 1 là tìm các itemset có frequency đạt yêu cầu và bước 2 là xác định các luật kết hợp tương ứng.
Để biểu diễn các itemset, các chuyên gia thường sử dụng đồ thị Hasse để thể hiện các itemset và sự liên kết cấu trúc giữa chúng.
Cho I = {A, B, C, D, E}, có d = 5 item, tổng số itemset khả thi là 25 – 1 = 31 itemset, không tính itemset rỗng. Chúng ta có mẫu Lattice như sau:
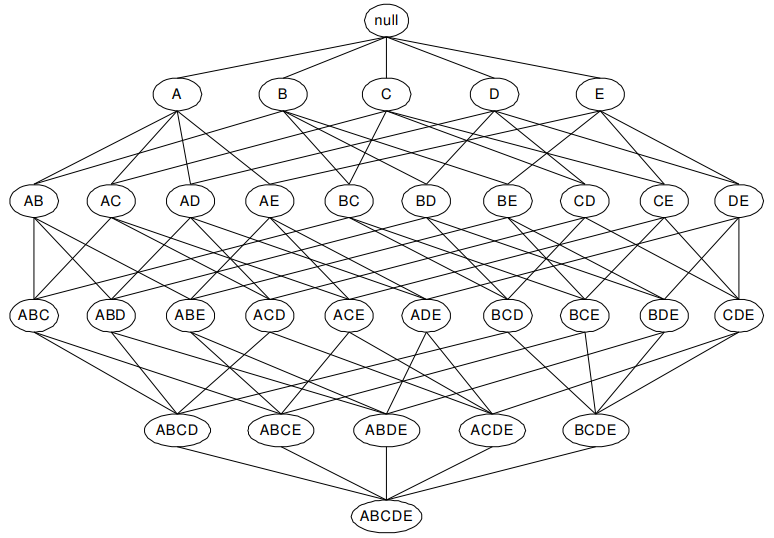
Sự khác biệt giữa các itemset giảm dần từ trên xuống, hoặc từ dưới lên nếu xoay hình lại. Nghĩa là lattice sẽ được chia thành 2 phần giới hạn, một phần: các itemset khác biệt nhất (không có điểm chung), một phần: các itemset gần giống nhau nhất nhưng không tuyệt đối (có nhiều điểm chung nhất nhưng không hoàn toàn giống nhau).
Do chỉ có 5 item riêng biệt nên Lattice nhìn gọn, nếu trong dữ liệu thực tế, số item riêng biệt là rất nhều thì lattice sẽ rất lớn, việc xác định tất cả itemset sẽ rất khó khăn. Các chuyên gia gọi đây là vấn đề không thể kiểm soát được “search space” – không gian tìm kiếm itemset sẽ lớn dần khi số item riêng biệt tăng lên.
Tuy nhiên đối với tập dữ liệu ít item thì lattice hỗ trợ xác định và không bỏ sót các itemset nào.
Ngoài ra, khi biết được các itemset nào không đạt yêu cầu về tần suất xuất hiện, frequency, hay tỷ lệ support tối thiểu, chúng ta sẽ nhanh chóng loại bỏ những itemset này, đồng thời là các rules khả thi xác định được trên lattice (theo định lý phát biểu bởi thuật toán Apriori mà chúng tôi sắp nói tới dưới đây)
Để giảm độ phức tạp trong tính toán frequency, giải pháp các chuyên gia nhắm đến:
- Giảm càng nhiều các itemset không cần thiết phân tích nếu có thể
- Giảm công đoạn đối chiếu các itemset với từng giao dịch trong dữ liệu
Trong phần 2 lần này chúng ta sẽ tìm hiểu về cách giảm các itemset cần tìm thông qua sử dụng thuật toán Apriori để thu nhỏ “search space”.
Thuật toán Apriori
Apriori hay A-priori là thuật toán Data mining nổi tiếng và phổ biến, được phát hiện bởi 2 chuyên gia Agrawal và Srikant năm 1994, giới thiệu lần đầu hội nghị “Very large Data Base” lần thứ 20 cùng năm.
Tên của thuật toán dựa trên cách vận hành của nó. Apriori sử dụng những hiểu biết trước đó – tiếng anh gọi là “prior” – về tính chất của các frequent itemset tìm thấy trong tập dữ liệu để khai phá những association rule. Apriori triển khai một “quá trình tìm hiểu” những itemset lặp đi lặp lại theo từng cấp độ của tập phần tử, ví dụ sau khi xác định k-itemset được cho là xuất hiện phổ biến với frequency đạt yêu cầu tối thiểu, thì Apriori sẽ sử dụng k-itemset để khám phá tiếp (k+1) – itemset.
Ví dụ một tập hợp các itemset chỉ có 1 phần tử, có tên S1 trong đó các item được xác định tần số xuất hiện và đạt yêu cầu tỷ lệ support tối thiểu. Sau đó S1 sẽ được dùng để tìm ra S2 là tập hợp các 2-itemset có 2 phần tử, và đảm bảo yêu cầu về tính phổ biến, tương tự S2 sẽ được dùng để tìm ra S3 – tập hợp các 3-itemset có 3 phần tử cũng đảm bảo yêu cầu về tính phổ biến, cứ thể S3 sẽ được dùng để tìm S4 cho đến khi hết k-itemset cần tìm.
Để quá trình trên được diễn ra, thì thuật toán Apriori đưa ra định lý cần tuân theo:
Nếu một tập phần tử hay itemset được coi là phổ biến – frequent (đạt được tỷ lệ Support tối thiểu) thì các tập con của nó – hay còn gọi subsets cũng sẽ phổ biến – frequent. Ngược lại một tập phần tử hay itemset được cho là không phổ biến – infrequent (không đạt tỷ lệ Support tối thiểu) thì các tập lớn hơn có chứa itemset này cũng sẽ infrequent.
Tất cả những itemset nào không phổ biến nên được loại bỏ, vì các association rule được khai phá từ chúng sẽ không đáp ứng tỷ lệ support.
Ví dụ một itemset gồm 2 phần = {A, B} được cho là không frequent, tần số xuất hiện, tỷ lệ support tối thiểu không đạt yêu cầu đề ra trước đó, thì cho dù có thêm item nào vào {A, B} cũng không cải thiện được frequent và tỷ lệ support.
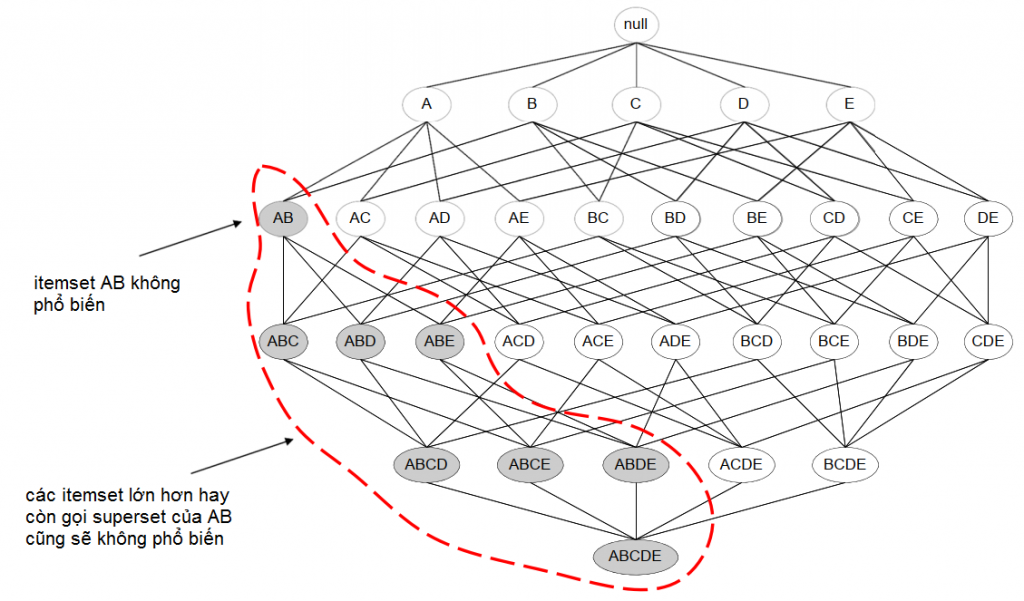
Các bạn hiểu đơn giản thế này: nếu AB đã ít xuất hiện trong tập dữ liệu, thì ABC, ABD, ABE những itemset có chứa AB làm sao xuất hiện nhiều được? Do đó nếu {A, B} không phổ biến thì các superset cũng vậy, không cần xét tiếp mà có thể loại bỏ bớt. Ở đây trong mô hình Lattice, các chuyên gia gọi là “Pruning tree” ngắt nhánh – giống trong C&T. Nhờ vậy, chúng ta đã bỏ bớt được các itemset không cần thiết, giảm được thời gian, công sức đi tìm frequency của chúng để đánh giá.
Ví dụ ngược lại giả sử itemset ABC – {A, B, C} là frequent thì các tập con của nó {A,B}, {A,C}, {B,C}, {A}, {B}, {C} cũng sẽ frequent
Định lý hay hướng tiếp cận của Apriori có tên gọi khác là anti-monotonicity, chống sự đơn điệu. Giải thích thuật ngữ: monotonic nghĩa là đơn điệu, nếu một function, một hàm số chỉ có xu hướng tăng, đồng biến, xu hướng giảm, nghịch biến thì được gọi là đơn điệu – monotonic, còn nếu vừa có tăng, vừa có giảm thì không được gọi là đơn điệu – non-monotonic.
Xét ở trường hợp Association rules, việc loại bỏ hay giữ lại dựa trên đánh giá frequency của các itemset diễn ra 2 hướng như 2 ví dụ ở trên nếu 1 itemset frequent thì các subset sẽ frequent (monotone), mà nếu itemset ấy infrequent thì các superset sẽ infrequent (anti-monotone). Mục đích áp dụng thuật toán Apriori chính là giảm bớt các itemset không phổ biến để loại bỏ chúng. Do đó có thể gọi tính chất của Apriori là anti-monotonicity
Một lưu ý quan trọng khác:
Gọi I là tập bao gồm số d các item riêng biệt trong tập dữ liệu, G là tập các itemset mỗi itemset chứa số k các item khác nhau. G = 2d – 1
Gọi s là tỷ lệ support, giả sử có X, Y là 2 itemset thuộc G, và itemset X là tập hợp con của Y:
∀ X, Y ∈ G: (X ⊆ Y) → s(X) ≥ s(Y) (1)
Tỷ lệ support của Y sẽ luôn nhỏ hơn tỷ lệ support của X hay tỷ lệ support của superset luôn nhỏ hơn tỷ lệ support của tập con, subset. Đây là anti-monotone. Theo cấu trúc lattice ở trên, thì tỷ lệ support sẽ giảm từ trên xuống, từ itemset cấp thấp xuống itemset cấp cao hơn.
Còn nếu là monotone, cấp itemset càng cao, thì tỷ lệ support càng cao:
∀ X, Y ∈ G: (X ⊆ Y) → s(X) ≤ s(Y) (2)
Tức tỷ lệ support của superset sẽ con hơn tỷ lệ support của subset. Tuy nhiên nó lại không đúng với thực tế.
Ví dụ nói tỷ lệ khách hàng mua {Ngũ cốc, sữa, nước giải khác} cao hơn tỷ lệ khách hàng mua {Ngũ cốc, sữa} liệu có hợp lý? tỷ lệ khách hàng mua {Ngũ cốc, sữa, nước giải khác} đã bao gồm tỷ lệ khách hàng mua {ngũ cốc, sữa} thì cần gì xét tiếp, sẽ không có ý nghĩa.
Mặt khác nếu chúng ta nói trong số những người mua cả {Ngũ cốc, sữa} thì không hẳn sẽ mua nước giải khác, họ sẽ mua thứ khác thì sao ví dụ mỳ gói? Như vậy tỷ lệ khách hàng mua ngũ cốc, sữa và cả nước giải khác sẽ có thể thấp hơn hoặc bằng tỷ lệ khách hàng mua ngũ cốc, sữa.
s{ngũ cốc, sữa} = s{ngũ cốc, sữa, nước giải khác} + s{ngũ cốc, sữa, mỳ gói}
Do đó định lý số (1) được xem là định lý chính cho các thuật toán khai phá luật kết hợp hơn. Nhắc lại lần nữa: trong apriori, tỷ lệ support của superset – tập lớn sẽ không thể vượt qua tỷ lệ support của subset – tập con.
Xác định những frequent itemset trong tập dữ liệu
Chúng ta đi vào bước đầu tiên của thuật toán Apriori trong khai phá luật kết hợp. Lấy lại ví dụ ở trên:
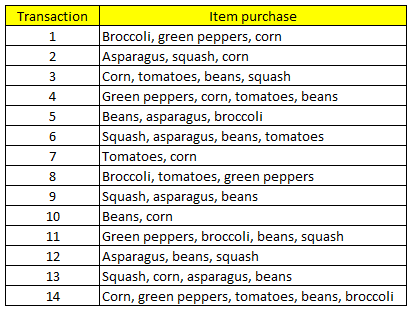
Đầu tiên xác định itemset có 1 item và tính tần số xuất hiện. Giả định minsupport = 28%, tức frequency thấp nhất bằng 4 thì itemset đạt yêu cầu về tỷ lệ support và sẽ có ý nghĩa
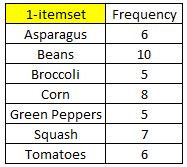
Các 1-itemset đều có tần số xuất hiện trên 4, nên ở bước này không loại bỏ 1-itemset nào. Tiếp theo chúng ta sẽ sử dụng dữ kiện từ 1-itemset để tìm 2-itemset – mỗi tập phần tử có 2 item.
Gọi Fk là tập các itemset có chứa k phần tử được cho là frequent hay đạt tỷ lệ support tối thiểu.
Như vậy F1 = {Asparagus, Beans, Broccoli, Corn, Green Peppers, Squash, Tomatoes}
Cho Ck là tập các k-itemset được xác định dựa trên các dữ kiện trước đó. Để tìm Ck chúng ta sẽ kết hợp các item trong Fk-1 lại với nhau.
Chúng ta có = 21 2-itemset (theo công thức tổ hợp 7C2)
Tập C2 chứa tất cả các 2-itemset sau, đã được count số lần xuất hiện:
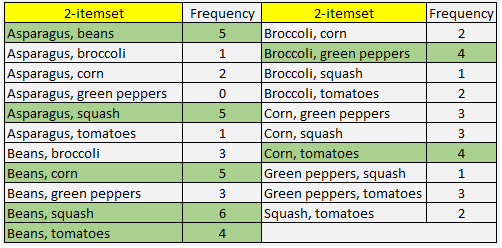
Các 2-itemset được tô xanh là đạt yêu cầu về frequency.
Chúng ta có F2 = {Asparagus, beans}, {Asparagus, squash}, {Beans, corn}, {Beans, squash}, {Beans, tomatoes}, {Broccoli, green peppers}, {Corn, tomatoes}
Giải thích lý do tại sao phải lấy F1 để tạo C2 và F2 đó chính là vì định lý của thuật toán Apriori.
Nếu (k-1) itemset không đạt frequency tối thiểu, không được coi là phổ biến thì không thể là tập con của các k-itemset lúc sau, tức các itemset bậc (size) cao hơn sẽ không được hình thành nếu các tập con của chúng không đáp ứng tỷ lệ support tối thiểu.
Chúng ta sử dụng tiếp F2 để tạo C3 và tìm F3
Lúc này chúng ta sẽ kết hợp 2 itemset thuộc F2 có cùng chung 1 item trước đó với nhau. Ví dụ {Beans, corn} và {Beans, squash} sẽ tạo thành {Beans, corn, squash} (ban đầu chúng ta ưu tiên thứ tự theo bảng chữ cái)
Như vậy chúng ta có tập C3 gồm các 3-itemset dưới đây:
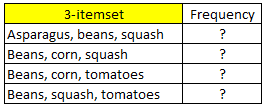
Tìm frequency như thế nào? Có cần xác định frequency của từng 3-itemset hay không?
Đối với tập dữ liệu nhỏ như ví dụ này thì chúng ta có thể đếm số lần xuất hiện của mỗi 3-itemset tuy nhiên với mẫu dữ liệu lớn hơn thì việc làm này rất mất thời gian. Khác với F1 sang F2, từ F2 đến F3 chúng ta có thể sử dụng định lý của Apriori để xác định:
Ví dụ 3-itemset đầu tiên {Beans, corn, tomatoes} được tạo thành bởi 2 tập con {Beans, corn} và {Beans, tomatoes} và cả 2 2-itemset cùng với {corn, tomatoes} này trước đó đã đạt tiêu chuẩn frequency, như vậy liệu không cần đánh giá {Beans, corn, tomatoes}, chúng ta có thể suy ra luôn {Beans, corn, tomatoes} đã “pass” bài test? Điều này sai hoàn toàn, nếu count các bạn có thể thấy {Beans, corn, tomatoes} chỉ xuất hiện 3 lần < 4, nên sẽ bị loại.
Cũng vì thế để tránh sơ hở này, Apriori không có đưa ra định lý: “Nếu tất cả (k-1)-itemset (subset, tập con) là frequent, thì k-itemset lúc sau sẽ frequent” mà sẽ là ngược lại. Vì thế gọi là anti-monotonicity.
Tiếp tục ở 3-itemset thứ 2 và thứ 4 {Beans, corn, squash} có 2-itemset là {corn, squash}có frequency < 4; {Beans, squash, tomatoes} có 2-itemset là {squash, tomatoes} < 4. Như vậy sẽ bị loại bỏ, do tập con không xuất hiện phổ biến, thì tập lớn hơn chứa tập con đó cũng sẽ không xuất hiện phổ biến. Cả 3-itemset {Beans, corn, squash} và {Beans, squash, tomatoes} có số lần xuất hiện 3, và 2 đều < 4.
- Đến điểm này các bạn sẽ thấy được vấn đề: nếu tất cả subset (k-1)-itemset là frequent thì chúng ta chỉ tạm thời chưa loại bỏ các superset k-itemset lúc sau hay chưa vội ngắt nhánh trên lattice, mà cần xác định thêm frequency để xem có đạt yêu cầu hay không. Nhưng nếu (k-1)-itemset là infrequent thì chắc chắn loại bỏ ngay k-itemset, mà không cần làm gì thêm
Các bạn tự kiểm tra thử {Asparagus, beans, squash}, nếu đúng thì 3-itemset này đã đạt yêu cầu.
Quay trở lại với ví dụ, như vậy chúng ta có 1 tập 3-itemset tốt nhất để khai phá luật kết hợp. Vì bài viết có giới hạn nên chúng tôi khai phá luật kết hợp của chỉ 3 item mà thôi, các bạn có thể tự làm F4 đến F7 nếu có thời gian
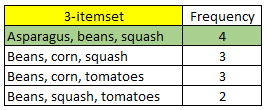
Nào cùng nhìn lại giả sử nếu không dùng Apriori và dùng Apriori thì sẽ khác biệt như thế nào về tính phức tạp, chi phí tính toán.
Chúng ta sẽ lấy chỉ tiêu là số k-itemset tổng thể cần đánh giá tỷ lệ Support để so sánh
Có 7 item
- Không dùng Apriori
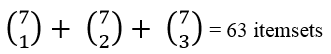
- Dùng Apriori
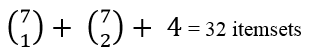
Như vậy số itemset cần kiểm tra khi dùng Apriori giảm gần phân nữa so với hướng tiếp cận sơ khai của Association rules.
Tuy nhiên trong chính Apriori thì những step chúng ta vừa làm ở trên cũng chưa thực sự hiệu quả, chúng ta vẫn có thể cải thiện hơn nữa tốc độ thực hiện. Ở bài viết sau chúng tôi sẽ nói về vấn đề này
Khai phá các luật kết hợp từ Frequent k-itemset tìm được
Chúng ta sang bước thứ 2 quan trọng chính là từ itemset tìm được sẽ có được bao nhiêu association rules.
Với mỗi k-itemset chúng ta sẽ có 2k – 2 luật kết hợp. Ví dụ cho 2-itemset = {A, B}, vậy có 22 – 2 = 2. A => B, B => A. Trừ 2 ra có nghĩa là chúng ta không tính trường hợp một trong Antecedent, Consequent là tập rỗng.
Cho 3-itemset = {A, B, C} vậy số association rules tiềm năng = 23 – 2 = 6
{A} => {B; C} {B} => {A; C} {C} => {A; B} {A; B} => {C} {A; C} => {B} {B; C} => {A}
Cách khai phá luật kết hợp từ 1 frequent itemset Y chính là chia itemset thành 2 phần, 1 phần sẽ là 1 tập con gọi là X và 1 phần còn lại Y – X. Luật kết hợp X => Y – X sẽ phải đạt tỷ lệ Confidence cao hoặc tối thiểu theo yêu cầu phân tích, hoặc dựa trên mục đích phân tích, và kinh nghiệm của chuyên gia.
Việc chọn lựa Association rules dựa trên tỷ lệ Confidence là đảm bảo Apriori hay bất kỳ thuật toán khác khi tìm ra một luật kết hợp nào đó phải đảm bảo tiêu chí về Support và Confidence
Định lý thứ 2 được đưa ra ở bước này:
Nếu một luật kết hợp X -> Y – X không thỏa mãn tỷ lệ Confidence tối thiểu thì luật kết hợp X’ -> Y – X’ cũng sẽ không thỏa mãn, với X’ là tập con bất kỳ thuộc X
Ví dụ {A, B, C} là 3-itemset thỏa mãn tỷ lệ Support, nhưng luật kết hợp {A, B} => {C} lại không thỏa mãn tỷ lệ Confidence, nên {A} => {C}, và {B} => {C} cũng sẽ không đạt tỷ lệ Confidence theo yêu cầu.
Quay trở lại với ví dụ ở trên:
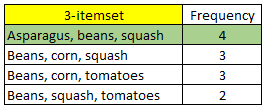
Đầu tiên từ Y – tập 3-itemset frequent chúng ta sẽ tìm tất cả các tập X là tập con của 3-itemset này, và xem là phần thứ nhất, tập con max chỉ có 2 item.
X = {Asparagus}, {beans}, {squash}, {Asparagus, beans}, {Asparagus, squash}, {beans, squash}
Chúng ta sẽ có 23 – 2 = 6 luật kết hợp. Trong thực tế, một công ty chỉ tập trung dự báo 1 sản phẩm tiềm năng nhất mà khách hàng có thể mua tiếp, vì nó không phức tạp và dễ chính xác hơn. Nên ở đây X chúng tôi tạm thời xét 2-itemset trước là phần Antecedent – phần nguyên nhân và Consequent là hệ quả.

Giả sử tỷ lệ confidence tối thiểu là 80%, thì luật kết hợp đầu tiên sẽ được chọn, bên cạnh đạt tiêu chí về Support, Confidence thì Lift cũng không gần quá 1.
“Nếu khách hàng mua asparagus và beans thì sẽ mua squash” tỷ lệ các giao dịch có cả asparagus, beans, và squash xuất hiện trong 14 giao dịch là 29%, tỷ lệ khách hàng mua asparagus và beans rồi mua tiếp squash là 80% so với các sản phẩm được mua tiếp khác. Khả năng khách hàng mua squash sau khi mua asparagus và beans cao hơn 1.6 lần so với khách hàng thông thường.
Như vậy chúng tôi đã tìm hiểu qua thuật toán Apriori với ví dụ đơn giản. Ở bài viết tới chúng ta sẽ tìm hiểu tiếp cách thức cải thiện thuật toán Apriori thông qua việc tối ưu hóa, giảm chi phí, thời gian quá trình tính toán Frequency cho các itemset cũng như xác định luật kết hợp của chúng.
Tài liệu tham khảo:
“Introduction to Data mining” – Pearson, tác giả Tan, Steinbach, Kumar
“Data Mining Concepts and Techniques” – Jiawei Han, Micheline Kamber, Jian Pei
“Data mining and predictive analytics” – Daniel T. Larose
“Principles of Data mining” – Max Bramer
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English