Tiếp tục với chủ đề về Time series (chuỗi thời gian) thì ở bài viết trước phần 1 chúng ta đã tìm hiểu về khái niệm Time series là gì, mục đích phân tích dữ liệu dãy số thời gian và các ứng dụng trong lĩnh vực kinh doanh. Trở lại với phần 2 bài viết lần này BigDataUni và các bạn sẽ đi vào các chỉ số mổ tả dãy số thời gian, làm quen với phương pháp trung bình trượt Moving Average cách sử dụng chúng để phân tích xu hướng biến động của dữ liệu Time series.
Dành cho các bạn chưa xem qua phần 1:
Tổng quan về time series (chuỗi thời gian) (p.1)

Cũng giống như các dữ liệu trong thống kê nói chung thì dữ liệu dãy số thời gian cũng cần có các thông số hay chỉ số mô tả chúng. Mặt khác, các chỉ số sẽ hỗ trợ quá trình phân tích dữ liệu dãy số thời gian và dự báo được tốt hơn. Chúng ta cùng tìm hiểu qua một số chỉ số quan trọng:
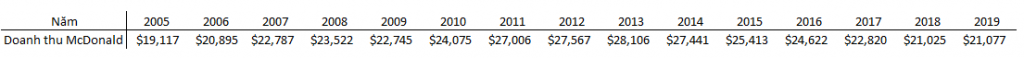
Chúng ta có dữ liệu doanh thu thuần của McDonald’s từ năm 2007 đến năm 2019 như trên, dữ liệu được lấy từ MacroTrends, đơn vị tính triệu USD.
Như đã nói ở bài viết trước, để nhận diện dữ liệu là Time series chúng ta không chỉ nhìn vô bảng số liệu mà còn phải thể hiện chúng trên đồ thị sử dụng biểu đồ đường hoặc biểu đồ cột, giống như Statista
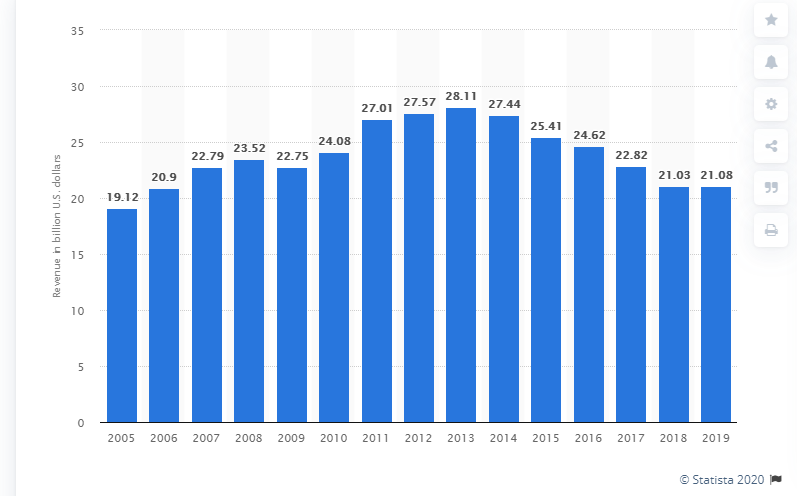
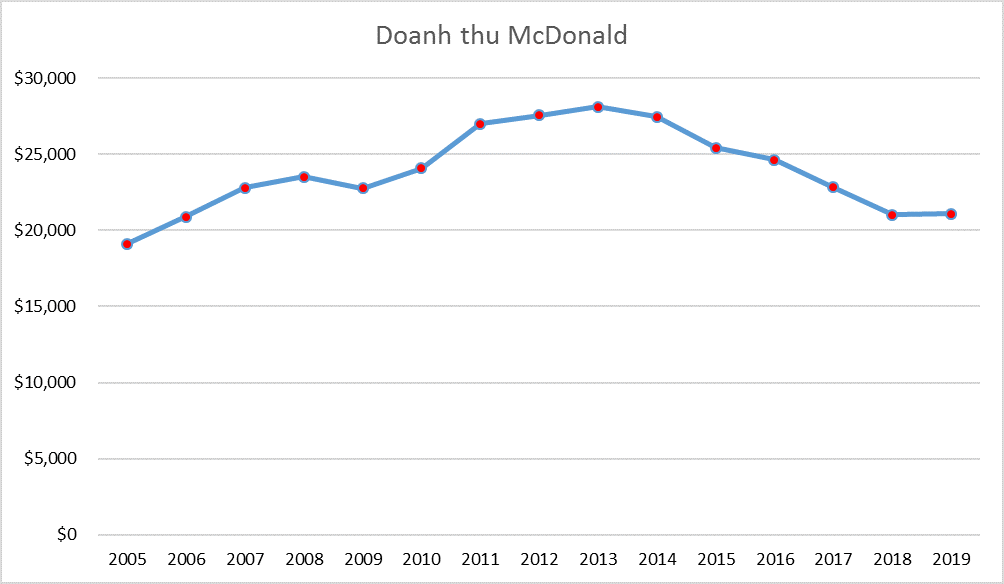
Sau khi thể hiện qua đồ thị chúng ta sẽ sử dụng các chỉ số để mô tả dữ liệu time series này
- Giá trị hay Mức độ Trung bình của dãy số
Trung bình của dãy số thời gian là giá trị tuyệt đối đại diện cho dãy số, thể hiện mức độ tập trung, điển hình của các giá trị có trong dãy số của đối tượng nghiên cứu.
Về cách thức thu thập dữ liệu thì dữ liệu dãy số thời gian sẽ chia thành 2 loại chính là dãy số thời kỳ và dãy số thời điểm. Ví dụ thời kỳ, doanh thu trong năm 2019 của McDonald’s là 21.08 tỷ USD, ví dụ thời điểm, doanh thu toàn cầu của McDonald vào ngày 1/3/2019 là 56 triệu USD.
Số liệu thời kỳ thì có thể cộng lại để phản ánh giá trị của đối tượng nghiên cứu trong thời gian dài ví dụ tổng doanh thu 10 năm gần nhất của McDonald’s = 271.9 tỷ USD.
Giả sử dữ liệu doanh thu vào ngày 1 của các tháng dưới đây của McDonald’s như sau:
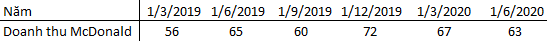
Chúng ta đâu thể nói doanh thu năm 2019 của McDonald’s là 253 triệu USD? Nó chỉ là doanh thu của 4 ngày mà thôi.
Nhắc lại một chút về nội dung bài viết trước. Quay lại với công thức tính mức độ trung bình.
Thì đối với thời kỳ chúng ta có công thức như sau:
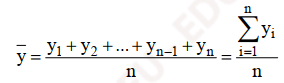
i là thứ tự các thời kỳ trong dãy số thời kỳ i = 1, 2,…, n, yi là mức độ thứ i trong dãy số
Ví dụ doanh thu trung bình của McDonald’s từ 2005 đến 2019 bằng tổng các giá trị doanh thu chia cho tổng số năm.
Ytb = (19117 + 20895 + … + 21077)/ 15 = 23881. Trung bình doanh thu mỗi năm sẽ là 23.8 tỷ USD.
Các bạn lưu ý: Y1 = Y2005 Trong cách tính toán để tránh nhầm lẫn, các bạn cứ đặt mốc đầu tiên là 1 và cứ tăng dần lên.
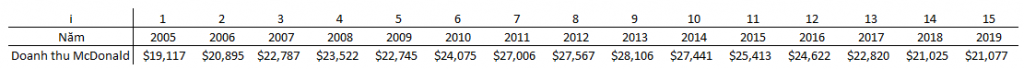
Đối với dữ liệu thời điểm mà khoảng cách giữa các thời điểm là bằng nhau như dưới đây
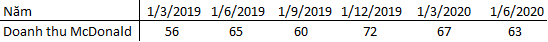
Mức độ trung bình được tính theo công thức như sau:
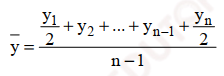
Giá trị tính được: ytb = (56/2 + 65 +60 + 72 + 67 + 63/2)/ (6 – 1) = 64.7 triệu USD
Đối với dữ liệu thời điểm mà khoảng cách giữa các thời điểm ghi nhận dữ liệu là không bằng nhau và thời gian nghiên cứu hay theo dõi là kéo dài liên tục.
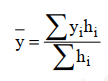
Với hi là độ dài thời gian ứng với mức độ thứ i
Giả sử số lượng nhân viên McDonald’s tại các chi nhánh trong 1 thành phố ghi nhận như sau
Ngày 1/1/2019 là 225 người, ngày 10/1/2019 là 220 người, ngày 15/1/2019 là 240 người, ngày 23/1/2019 là 235 người, ngày 31/1/2019 là 250 người
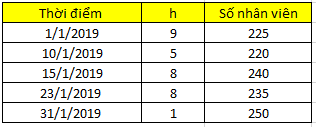
Ví dụ h1 = 9. Tức từ ngày 1/1 đến 9/1 có 9 ngày., 10/1 đến 14/1 có 5 ngày, tính tương tự cho các thời điểm còn lại riêng 31/1 là kết thúc thì tính luôn ngày 31, h5 = 1
Áp dụng công thức tính:
Ytb = [(225 x 9)+…+(250 x 1)]/ (9 + 5 + 8 + 8 + 1) = 231.4 làm tròn là 231 nhân viên/ ngày
- Lượng tăng (giảm) tuyệt đối của dãy số
Chỉ số này dùng để đánh giá sự thay đổi của đối tượng nghiên cứu giữa 2 thời điểm hoặc 2 thời kỳ nào đó
+ Lượng tăng (giảm) liên hoàn
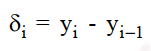
Với i = 2, 3, …, n
Lượng tăng giảm liên hoàn so sánh giữa 2 thời kỳ, 2 thời điểm liền kề nhau. δi > 0 thể hiện đối tượng nghiên cứu biến động tăng và ngược lại với δi < 0
Ví dụ δ14 = y14 – y13 = 21025 – 22820 = -1795
Doanh thu năm 2018 của McDonald’s giảm 1.8 tỷ USD so với năm 2017
Từ bảng số liệu doanh thu từ 2005 đến 2019 ở trên chúng ta tính được lượng tăng (giảm) tuyệt đối như sau:
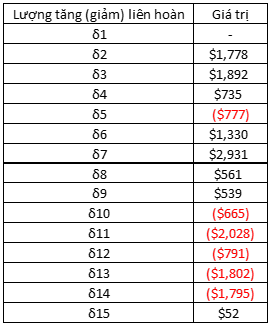
+ Lượng tăng (giảm) tuyệt đối định gốc
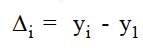
Chỉ số phản ánh biến động của đối tượng trong thời gian nghiên cứu so với điểm bắt đầu, thời gian gốc
Với i = 2, 3,…, n
Ví dụ, Δ8 = y8 – y1 = y2012 – y2005 = 27567 – 19117 = 8450
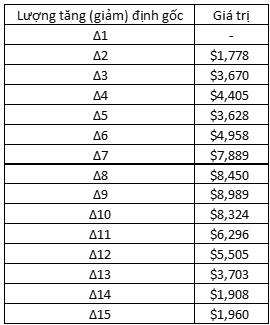
+ Lượng tăng (giảm) tuyệt đối trung bình
Lượng tăng (giảm) tuyệt đối trung bình chung trong thời gian nghiên cứu, công thức:
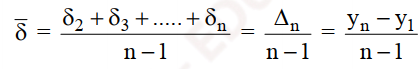
Ví dụ lượng tăng (giảm) tuyệt đối trung bình chung của McDonald’s năm 2005-2019 tính theo công thức trên là: 140 triệu USD. Tức trung bình mỗi năm trong giai đoạn 2005-2019, McDonald’s tăng 140 triệu USD doanh thu.
Tuy nhiên nếu các bạn nhìn lại bảng tính lượng tăng (giảm) tuyệt đối liên hoàn thì có thể thấy mỗi năm Mc.Donald’s tăng hoặc giảm với giá trị lớn hơn nhiều so với con số 140 triệu, sai lệch rất lớn.
Do đó chỉ số này chỉ phù hợp trong trường hợp đối tượng nghiên cứu biến động đều không quá khác biệt qua các năm.
- Tốc độ phát triển
Là các chỉ số đánh giá đối tượng nghiên cứu phát triển như thế nào với tốc độ ra sao trong thời gian nghiên cứu.
+ Tốc độ phát triển liên hoàn
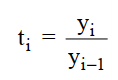
Chỉ số phản ánh tốc độ phát triển của đối tượng nghiên cứu qua 2 thời kỳ hay thời điểm liền nhau:
Ví dụ t9= y9/ y8 = 28106/ 27567 = 1.019 hay 101.9%. Doanh thu năm 2013 McDonald’s tăng với tốc độ 101.9% so với năm 2012. Các bạn thử tính từ t2 đếm t15 nhé.
+ Tốc độ phát triển định gốc
Chỉ số phản ánh tốc độ phát triển của đối tượng nghiên cứu giữa một kỳ bất kỳ so với kỳ gốc hay kỳ đầu tiên
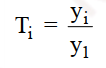
Ví dụ T10 = y10/y1 = 27441/ 19117 = 1.435 hay 143,5%. Doanh thu năm 2014 của McDonald’s so với năm gốc 2005 tăng với tốc độ 143.5%
2 công thức quan trọng về mối quan hệ giữa 2 chỉ số này:
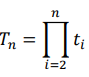
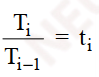
+ Tốc độ phát triển trung bình
Cũng giống như lượng tăng giảm tuyệt đối, chỉ số tốc độ phát triển trung bình thể hiện tốc độ phát triển chung hay đại diện của đối tượng nghiên cứu trong suốt khoảng thời gian.
Công thức
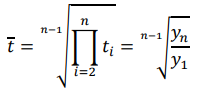
Ví dụ t = (y2019/ y2005)15-1 = (21077/ 19117)1/14 = 1.007 hay 100.7%
Trung bình hàng năm doanh thu McDonald’s phát triển với tốc độ 100.7%
- Tốc độ tăng (giảm)
So sánh giữa 2 thời kỳ, hay 2 thời điểm, đối tượng nghiên cứu đã tăng (giảm) bao nhiêu %
+ Tốc độ tăng (giảm) liên hoàn
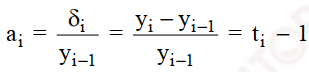
Ví dụ a15 = t15 – 1 = (y15/ y14) – 1 = (y2019/ y2018) – 1 = 0.0024
Doanh thu năm 2019 của Mc.Donald’s tăng 0.24% so với năm 2018.
+ Tốc độ tăng (giảm) định gốc:
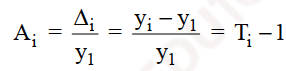
Ví dụ A15 = T15 – 1 = (y15/ y1) – 1 = (21077/19117) – 1 = 0.1
Doanh thu năm 2019 của Mc.Donald’s tăng 10% so với năm 2005
+ Tốc độ tăng (giảm) trung bình
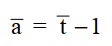
Ví dụ a = 1.007 – 1 = 0.007 = 0.7%. Tốc độ tăng doanh thu trung bình mỗi năm của McDonald’s là 0.7%. Tuy nhiên số liệu không chính xác khi doanh thu của McDonald’s qua các năm biến động không đều.
- Giá trị tuyệt đối 1% của tốc độ tăng (giảm) liên hoàn
1% tăng hoặc giảm của đối tượng nghiên cứu qua 2 thời kỳ, hoặc 2 thời điểm là bao nhiêu với giá trị cụ thể.
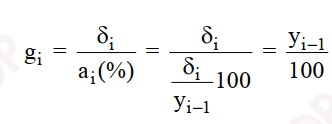
Ví dụ g15 = y14/ 100 = 21025/100 = 210.25. Tức 1% tăng trong doanh thu năm 2019 của Mc.Donald’s tương ứng 210 triệu USD.
Như vậy chúng ta đã tìm hiểu xong các chỉ số mô tả dãy số thời gian. Chắc nhiều bạn có thể thắc mắc tại sao những chỉ số đơn giản như vậy chúng tôi lại trình bày cụ thể. Lý do vì chúng rất hữu ích! Các chỉ số sẽ hỗ trợ các bạn hiểu và diễn giải tốt hơn biến động của đối tượng nghiên cứu theo thời gian chi tiết và cụ thể hơn về mặt lượng trong các báo cáo số liệu hay thuyết trình. Ngoài ra chúng sẽ còn xuất hiện trong các công thức phân tích Time series ở các phần sau.
Nhắc lại mô hình Additive và Multiplicative
Ở bài viết phần 1 chúng ta đã đi qua các thành phần hay các pattern trong dữ liệu Time series bao gồm Trend (xu hướng), Seasonal (tính mùa vụ), Cyclical (tính thời kỳ), Irregular (tính bất thường, ngẫu nhiên)
Cả 4 thành phần sẽ tạo thành mô hình nhân (Multiplicative) và mô hình cộng (Additive) cho dữ liệu dãy số thời gian
Mô hình Multiplicative:
Y = T.S.C.I
Mô hình Additive:
Y = T + S + C + I
Cụ thể nếu mức độ biến động theo thời vụ của các mốc thời gian trước đó bằng với mức độ biến động theo thời vụ của các mốc thời gian là bằng nhau, đường xu hướng là đường thẳng tuyến tính đi lên hoặc đi xuống, các biến động có thể định lượng được bằng con số cụ thể thì mô hình Additive sẽ phù hợp. Tuy nhiên nếu biến động theo mùa thay đổi theo thời gian, ngày càng nhỏ dần hoặc lớn dần ví dụ doanh thu tăng qua các năm do xu hướng dài hạn là các đường cong phi tuyến hướng lên hoặc hướng xuống, các biến động có thể xác định được bằng con số %, thì nên sử dụng mô hình Multiplicative.
Ví dụ các bạn xem qua các biểu đồ dưới đây sẽ hiểu hơn
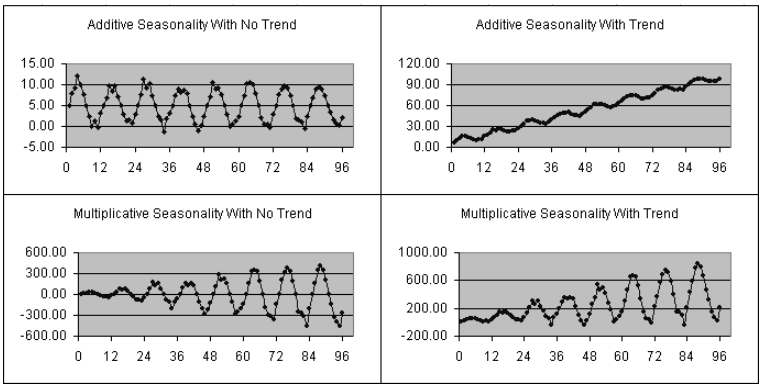
Nguồn hình: Oracle
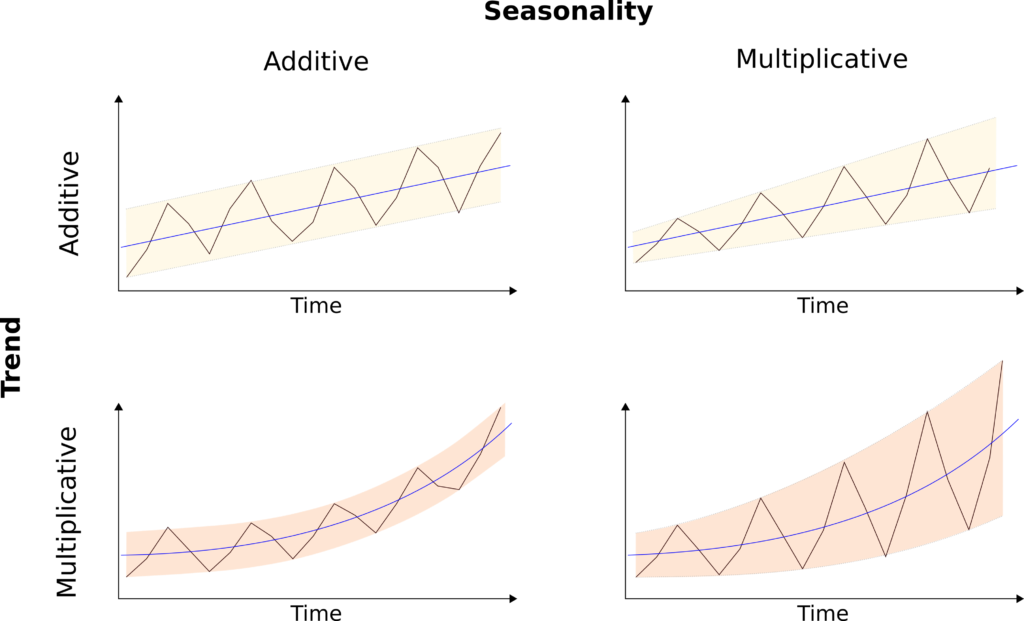
Nguồn hình: Daitan
Trong thực tế sự vật, hầu hết các hiện tượng đều sẽ phát triển, và các biến động ngẫu nhiên, hay mùa vụ trong tương lai có thể tác động mạnh hay yếu, bất định nên mô hình Multiplicative được sử dụng phổ biến hơn. Tuy nhiên điều này còn phụ thuộc vào chính dữ liệu thu thập về đối tượng nghiên cứu. Các phương pháp phân tích Time series ở bài viết này và bài viết phần 3 sẽ theo mô hình Multiplicative.
Xác định xu hướng biến động của dãy số thời gian
Xác định xu hướng biến động của dãy số thời gian là một trọng những bước quan trọng ban đầu để tìm hiểu về dữ liệu và là tiền đề để đưa ra các dự báo ở các giai đoạn sau. Mặc dù ngày nay các phần mềm phân tích, khai phá dữ liệu và các phần mềm thóng kê sẵn sàng hỗ trợ chúng ta xác định được ngay dãy số thời gian đang chuyển động như thế nào nhưng biết được các phương pháp nào và khi nào cần áp dụng, cũng như hiểu được bản chất của chúng để thực hiện phân tích chính xác là cực kỳ quan trọng.
Có 2 phương pháp chính trong xác định xu hướng biến động:
- Moving average (trung bình trượt): gồm 3 loại chính là Moving average đơn giản, Weighted moving average có gán trọng số và Exponential moving average – san bằng hàm mũ
- Trend model (sử dụng hàm số).
Trong bài viết này chúng ta sẽ làm quen Moving average dạng simple và weighted. Chúng tôi sẽ trình bày Exponential moving average và Trend model ở phần 3 do các phương pháp này được dùng cho dự báo nhiều hơn là tìm hiểu biến động do đó thích hợp để trình bày ở bài viết phần 3 tập trung về dự báo trong Time series
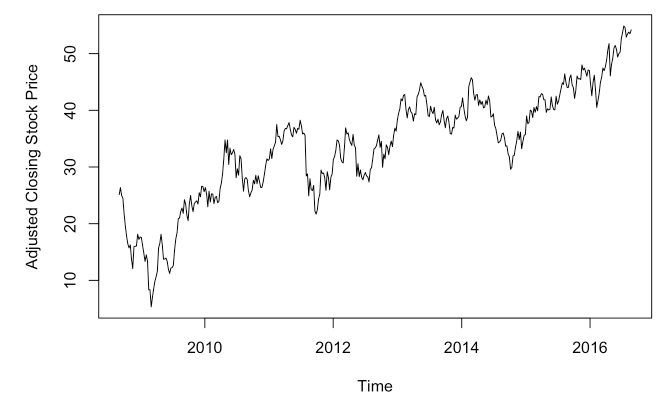
Nhìn thử biểu đồ ở trên, các bạn có đoán được xu hướng giá chứng khoán đóng cửa được điều chỉnh qua các năm là tăng ngay giảm hay không? Thực sự rất khó nói, giá biến động lên xuống không ngừng nhưng nếu nói theo thời gian thì nhìn chung các năm sau 2010 giá hầu như đều cao hơn. Chúng ta vẫn có thể thấy được xu hướng tăng, đi lên qua thời gian. Còn biểu đồ tiếp theo
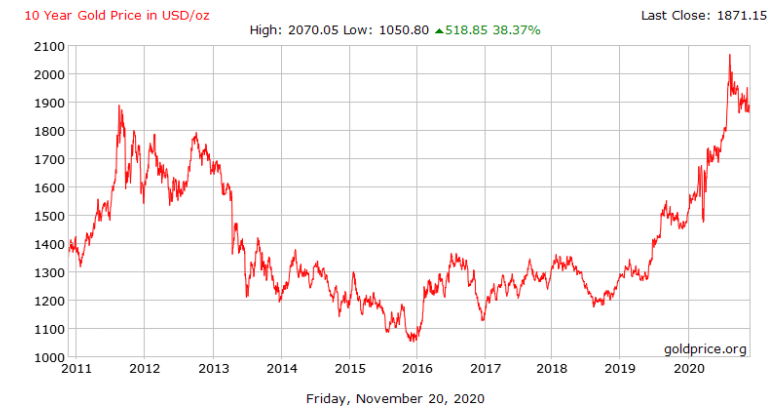
Nguồn hình: Goldprice.org
Phía trên là giá vàng thế giới cập nhật từ năm 2011 đến 2020. Nhìn qua thật sự chúng ta khó kết luận được xu hướng trong suốt thời gian nghiên cứu lý do là thời gian nghiên cứu quá dài hay giá vàng bản chất đã vốn không hề ổn định.
Trong thực tế, hầu như dữ liệu Time series đều không thể hiện rõ xu hướng của nó, nguyên nhân đến từ tác động của nhiều yếu tố ngẫu nhiên không thể kiểm soát hết. Phương pháp Moving Average ra đời với mục đích phần nào hạn chế các tác nhân ngẫu nhiên, cho chúng ta thấy được xu hướng chung tuy không chính xác tuyệt đối nhưng giúp chúng ta đưa ra đánh giá tổng thể đối tượng nghiên cứu đang biến động như thế nào.
Moving Average không phải “vũ khí” để tiêu diệt các yếu tố ngẫu nhiên trong thực tế vì đây là phương pháp chỉ áp dụng cho dữ liệu mà thôi. Nó cố gắng đưa dữ liệu hay đối tượng nghiên cứu về trạng thái không bị tác động bởi các yếu tố ngẫu nhiên và vận động một cách tự nhiên nhất.
Phương pháp Moving Average hoạt động dựa trên nguyên lý “các yếu tố ngẫu nhiên dù lớn hay nhỏ tại bất kỳ thời điểm cụ thể nào đều sẽ giảm tầm ảnh hưởng lên đối tượng nghiên cứu nếu chúng ta tính trung bình giá trị tại thời điểm đó với những giá trị lân cận hay liền kề”
Các phương pháp trung bình trượt còn được gọi là các phương pháp Smoothing dữ liệu hay làm nhẵn dữ liệu do nó biến các đường trên biểu đồ từ đầy nhiễu loạn do các yếu tố ngẫu nhiên đến các đường thẳng “mượt mà và bằng phẳng hơn”
Moving hay trượt nghĩa là tại từng giá trị, chúng ta sẽ cộng thêm các giá trị xung quanh để tính trung bình rồi thêm vào, cứ thế đến giá trị tiếp theo, và tiếp theo, trượt xuống đến giá trị cuối cùng của tập dữ liệu cũ. Lúc này tập dữ liệu cũ đã được thay thế bởi tập dữ liệu mới chứa tất cả các giá trị trung bình tính được. Nói có vẻ mơ hồ và khó hiểu, phần công thức và ví dụ phía dưới chúng tôi sẽ giải thích rõ hơn.
Bước quan trọng trong Moving Average đó là xác định vậy cần cộng thêm bao nhiêu giá trị liền kề để tính trung bình hay cụ thể hơn trong lý thuyết là xác định nhóm mức độ.
Ví dụ mức độ = 3, tức mỗi giá trị sẽ cộng thêm 2 giá trị khác liền kề để tính trung bình.
- Moving Average đơn giản:
Nếu dùng để dự báo cho giá trị tiếp theo
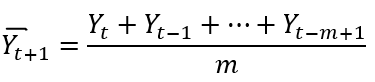
Nếu không dùng để dự báo:
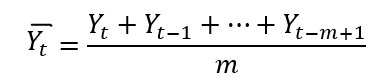
m là mức độ cần xác định.
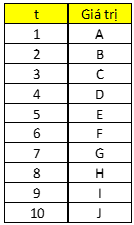
Giả sử chúng ta có bảng số liệu dạng Time series như trên. Ví dụ với m = 3 chúng ta tính trung bình trượt như sau:
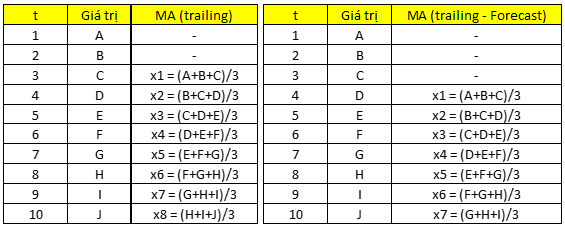
Áp dụng công thức:
Dự báo cho Y4 thì Y4 = (Y3 + Y2 + Y1)/ 3 = (C + B + A)/3, còn nếu không dùng để dự báo giá trị tiếp theo mà để hạn chế “độ nhiễu” của yếu tố ngẫu nhiên thì có thể tính MA tại Y3 = (A + B + C)/3. Các bạn xem lại 2 bảng ở trên.
Hướng tiếp cận này còn được gọi là Trailing – đường ray.
Cách khác:
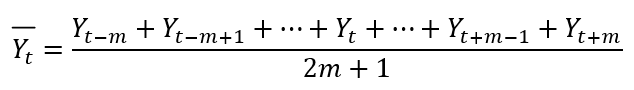
Theo bảng dưới đây thì khi mức độ = 3 thì m lúc này bằng 1. Các vị trí quan sát mà ở đó được tính MA đều là điểm chính giữa của dãy các số tính trung bình. Ví dụ t = 2, giá trị B là mid-point của (A => B => C), tương tự C nằm giữa B và D,…
Cả 2 cách này đều đáp ứng yêu cầu của MA là hạn chế tác động của yếu tố ngẫu nhiên nhờ vào phương pháp tính trung bình nhưng được ứng dụng riêng theo mục đích khác nhau.
- Nếu chúng ta muốn phân tích xu hướng của đối tượng nghiên cứu từ quá khứ đến tương lại một cách tổng thể thì Mid-point là thích hợp khi nó sử dụng cả giá trị quá khứ và tương lại để tính trung bình. Ví dụ tại t = 2, A là quá khứ của B, C là tương lai của B
- Nếu chúng ta muốn phân tích xu hướng để dự báo (gần giống Naïve Forecast) lấy giá trị quá khứ để tính giá trị tương lai thì phương pháp Trailing là phù hợp hơn.
Do tạm thời chúng ta chưa tìm hiểu đến giai đoạn dự báo trong Time series nên trong bài viết này chúng ta sẽ chỉ sử dụng trailing để phân tích biến động của dãy số. Hơn nữa dự báo sử dụng Trailing MA nghe có vẻ “phiêu lưu” và thiếu chính xác khi nó loại bỏ các yếu tố trong tương lai, chỉ dựa vào quá khứ để phán đoán. Nếu đối tượng nghiên cứu biến động rất thường xuyên do các tác động ngẫu nhiên thì Trailing MA cũng không giúp ích được gì hoặc ngược lại.
Vấn đề quan trọng thứ 2 khi áp dụng trung bình trượt đó chính là chọn mức độ, m hay 2m + 1 gọi chung là k nên bằng bao nhiêu,?
Việc xác định mức độ nó phụ thuộc khá nhiệu vào đặc tính của dữ liệu Time series, tính chất của đối tượng nghiên cứu và kinh nghiệm của người làm phân tích
Nếu người phân tích cho rằng trong dữ liệu Time series chỉ một số các giá trị gần kề là có sự liên quan, thì mức độ k nhỏ sẽ phù hợp. Nếu nhiều giá trị trong quá khứ được coi là có liên quan, thì mức độ k lớn hơn sẽ tốt hơn.
Ngoài ra, k nhỏ sẽ giúp theo dõi các biến động khác nhau trong một chuỗi thời gian nhanh hơn. Nhưng các giá trị lớn hơn của k sẽ hiệu quả hơn trong việc “làm phẳng” các biến động ngẫu nhiên theo thời gian và thể hiện đường xu hướng chung tốt hơn. Số k lớn thì sẽ ít số trung bình để vẽ đường xu hướng hay đánh giá xu hướng dễ bị “hời hợt”, số k nhỏ thì sẽ nhiều số trung bình, phân tích xu hướng sẽ nhanh và dễ dàng hơn. Hơn nữa, nếu dữ liệu biến động nhiều và mức độ biến động lớn, các giá trị có sự khác biệt, và chia làm các cấp độ theo độ lớn thì tăng số k lên và ngược lại. Có nhiều thứ cần phải xem xét, ở phần ví dụ chúng tôi sẽ nói rõ.
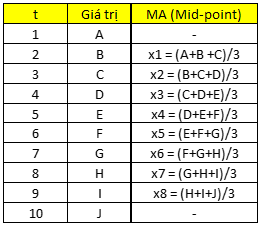
Ngoài ra nếu khó xác định được k mà dữ liệu Time series mà dữ liệu chia theo quý, tháng thì có thể lấy số quý, tháng làm số k. Chúng ta cùng đi qua thử ví dụ. Dưới đây là số liệu về “Net profit margin” (biên lợi nhuận) từ năm 2008 cập nhật đến 2020 ghi nhận theo quý của Mc.Donald’s
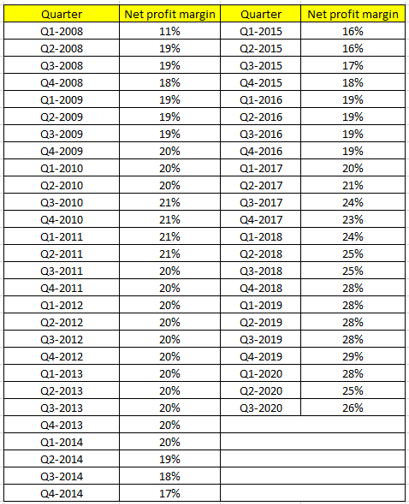
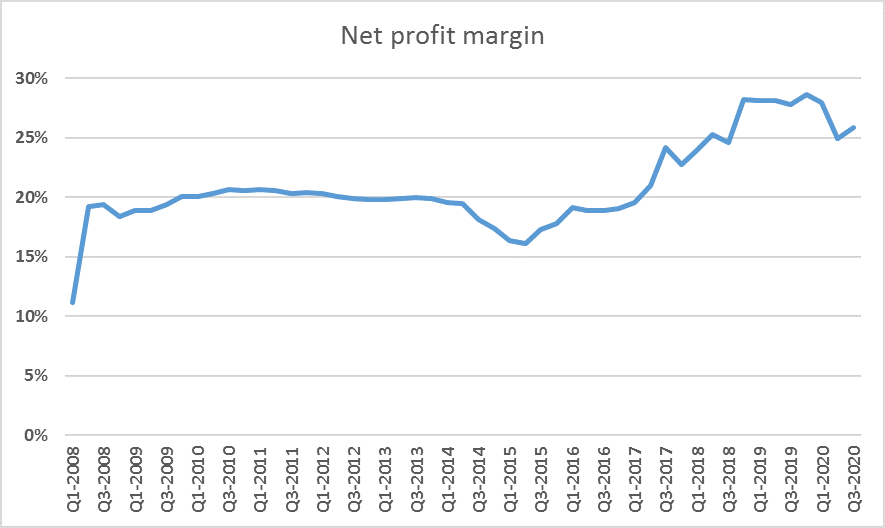
Bên trên là biểu đồ minh họa, thì nhìn qua chúng ta thấy dữ liệu time series này không thể hiện rõ xu hướng, và không mang tính mùa vụ.
Vì dữ liệu thu thập theo quý nên chúng ta lấy k = 4, sử dụng Trailing MA, dưới đây là kết quả
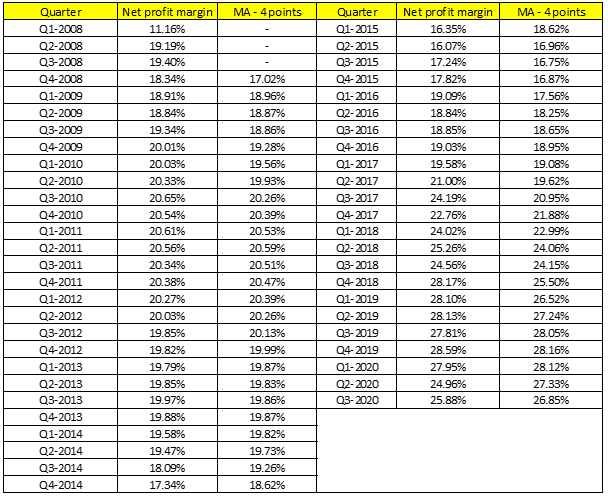
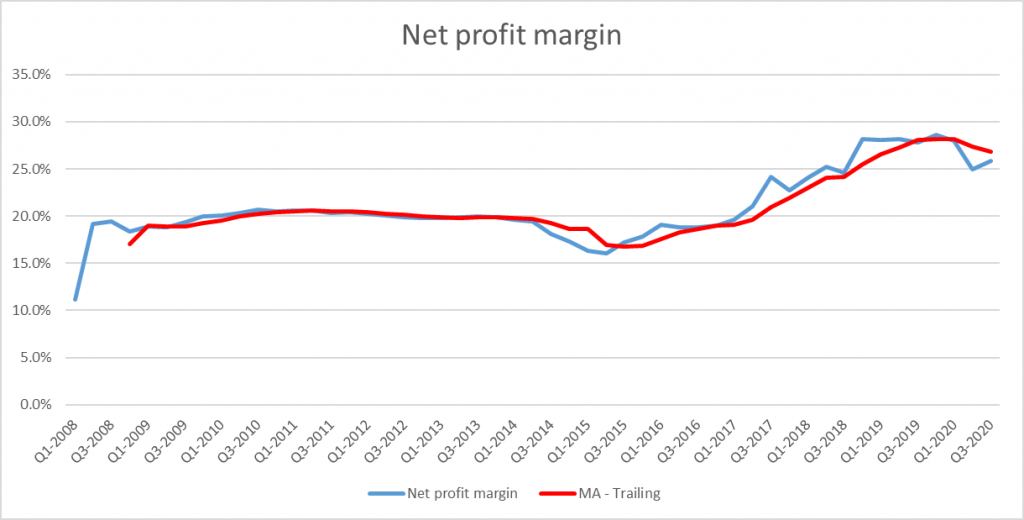
Chúng ta vẽ lại biểu đồ để xem thử:
Còn trường hợp sử dụng MA – Mid – point Chúng ta sẽ lấy mức độ k =3 tức 2m + 1 = 3 để tính
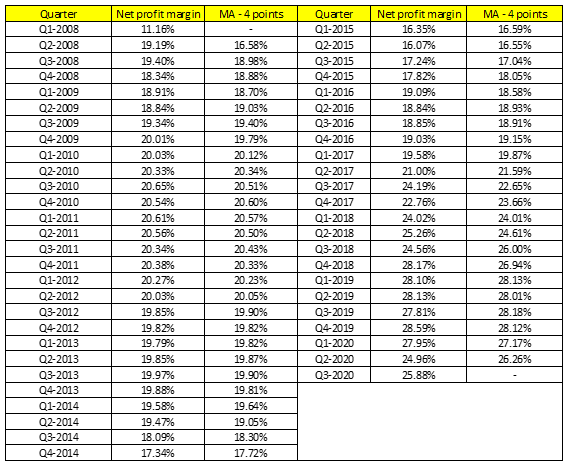
Ví dụ Q2 – 2008 = Y2MA = (11.16% + 19.19% + 19.40%)/3 = 16.58%
Chúng ta vẽ lại biểu đồ:
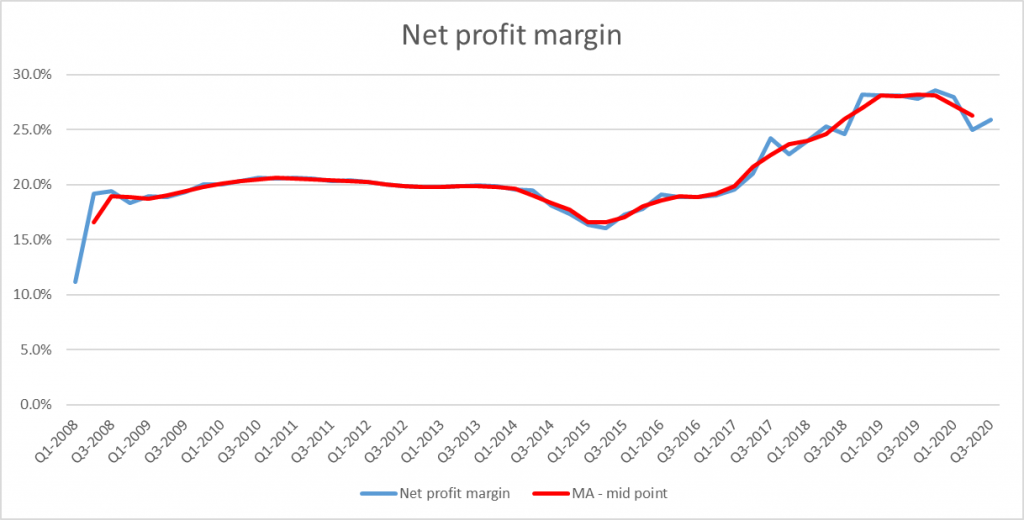
Cả 2 cách đều cho thấy xu hướng chung tăng lên của Net profit margin của Mc Donald’s từ năm 2015 đến 2020, trong khía cạnh kinh doanh thì McDonald đạt được lợi nhuận kinh doanh cao hơn và quản lý chi phí hiệu quả hơn so với trước năm 2015.
Các bạn có thể thấy khi sử dụng Mid-point với ít mức độ hơn thì đường Time series có vẻ mượt hơn Trailing mặc dù Trailing cũng cho thấy được xu hướng rõ, và đường xu hướng chung bằng phẳng hơn. Do có thể các giá trị không chênh lệch, không biến động quá nhiều, và độ lớn biến động nhỏ nên chúng ta khó xác định được Mid-point hay Trailing hoặc số k lớn hay nhỏ sẽ giúp xác định đường xu hướng tốt hơn.
Thay vì sử dụng ví dụ trên, chúng ta cùng nhìn qua các biểu đồ Time series với các mức độ khác nhau dưới đây để hiểu rõ hơn vấn đề:
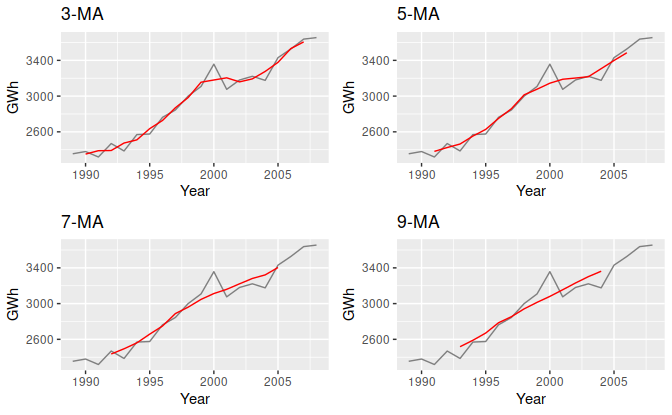
Nguồn hình: Otexts.com
Nếu nhìn 4 biểu đồ hơn thì chúng ta thấy rõ khi k từ 5 đến 9 đường xu hướng chung càng rõ ràng hơn, nhưng nó chỉ mô tả một phần của dãy số Time series mà thôi hay nói cách khác giống chúng tôi đề cập ở trên là “hời hợt”, còn khi k thấp thì chúng ta xác định được xu hướng toàn bộ dữ liệu nhưng theo các khoảng/ khung thời gian khác nhau tuy nhiên lại không thấy rõ được rõ 1 xu hướng chung.
Trong thực tế người ta sử dụng MA là để hỗ trợ việc dự báo nên MA dạng trailing được sử dụng phổ biến hơn. Thế nhưng khuyết điểm lớn nhất của MA chính là độ trễ trong dự báo. Chúng ta cùng xem lại biểu đồ Trailing:
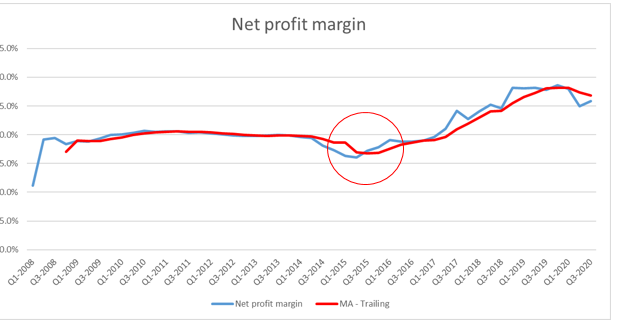
Tại thời điểm Q3 – 2015, Net profit margin của McDonald’s cho thấy dấu hiệu tăng lên nhưng đến Q1-2016, thì đường MA – Trailing mới cho thấy xu hướng tăng này. Tuy việc dự báo trễ Net profit margin không gây thiệt hại gì cho McDonald’s nếu họ đưa vô áp dụng thực tế, nhưng giả sử ở các lĩnh vực khác việc dự báo trễ sẽ đem lại hậu quả to lớn ví dụ trong lĩnh vực Trading hay đầu tư tài chính, các chuyên gia thường không sử dụng MA đơn giản mà họ sử dụng các công cụ chỉ báo kết hợp MA phức tạp hơn nguyên nhân là do độ trễ trong dự báo của MA thường khiến họ chậm nhịp và bị tổn thất về mặt lợi nhuận.
- Weighted Moving Average
Cũng giống như phương pháp tính trung bình có trọng số thì trong MA chúng ta cũng có thể tính trung bình trượt có gán trọng số cho các giá trị dựa trên kinh nghiệm phân tích, sự am hiểu đối tượng nghiên cứu. Ví dụ trong các trường hợp, chúng ta nhận định những giá trị gần hơn có sức ảnh hưởng lớn hơn lên giá trị dự báo nên sẽ có trọng số cao hơn trọng số của các giá trị ở các mốc thời gian cũ hơn.
Ví dụ như dữ liệu McDonald’s. Để tính trung bình trượt (Trailing – forecast ) tại Q3 – 2020 chúng ta sẽ tính:
YQ4-2020 = (27.95% + 24.96% + 25.88%)/3 = 26.85%
YQ4-2020 (Weighted) = [(1/6)*27.95% + (2/6)*24.96% + (3/6)*25.88%] = 25.918%
Kết quả trên là giả sử McDonald’s cho rằng Net profit margin của các quý gần hơn sẽ ảnh hưởng nhiều lên Net profit margin của quý dự báo tiếp theo nên Q3-2020 sẽ có trọng số cao hơn Q2-2020 và Q1-2020
Lưu ý các trọng số được đặt ra dựa trên ý kiến của người làm phân tích nhưng tổng phải bằng 1 ví dụ ở trên 1/6 + 2/6 + 3/6 = 1
Simple moving average và Weighted moving average chỉ cho chúng ta thấy được xu hướng biến động của đối tượng nghiên cứu nhưng không được dùng để dự báo nên hạn chế phần nào khả năng được ứng dụng trong nhiều lĩnh vực. Tuy nhiên nếu phải tìm các công cụ giúp khám phá hay “explore” Time series data tốt hơn thì chỉ có Moving average.
Và dĩ nhiên để dùng được Moving average trong dự báo, thì những chuyên gia dữ liệu từ lâu đã phát minh ra phương pháp Exponential moving average – là dạng đặc biệt của Weighted moving average, hay các phương pháp Exponential Smoothing nói chung – san bằng hàm mũ – để hỗ trợ đưa ra các dự báo chính xác hơn.
Tài liệu tham khảo
“Statistics for Business and Economics” của tác giả Paul Newbold, William L. Carlson, Betty M. Thorne
“The Practice of Statistics for Business and Economics” của tác giả David S. Moore và cộng sự
“PROBABILITY and STATISTICS for FINANCE” của tác giả Svetlozar (Zari) T. Rachev và cộng sự
“Statistics for Business and Economics” của các tác giả David R. Anderson, Dennis J. Sweeney, Thomas A. Williams và cộng sự
Ở bài viết phần 3, BigDataUni và các bạn sẽ tiếp tục sử dụng Moving Average để đánh giá biến động của 4 thành phần Trend (T), Seasonal (S), Cyclical (C), Irregular (I) trong mô hình nhân của Time series khi gặp trường hợp dữ liệu Time series hay đối tượng nghiên cứu có đủ 4 thành phần này. Và quan trọng nhất trong bài viết phần 3, chúng ta sẽ tìm hiểu về cách dự báo sử dụng các phương pháp Trend model.
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English