Ở bài viết trước chúng ta đã tìm hiểu qua cách phân tích tương quan để đánh giá mối quan hệ giữa 2 biến: quan hệ thuận, nghịch, hay không có quan hệ và tính bền vững quan hệ bằng hệ số tương quan (Coefficient of Correlation), đồng thời chúng ta đã xây dựng mô hình hồi quy tuyến tính đơn giản thông qua tìm hiểu cách triển khai các công thức tính hệ số hồi quy sử dụng phương pháp bình phương bé nhất, và thể hiện đường hồi quy trên đồ thị hàm số. Đồng thời chúng ta cũng đã làm quen với cách tính các giá trị SST (Total Sum of Squares), SSE (Sum of squares due to Errors), SSR (Sum of squares due to Regression) để tính hệ số xác định R2 (Coefficient of Determination), thể hiền phần tỷ lệ biến thiên của y mà chúng ta có thể giải thích bởi mối quan hệ tuyến tính giữa x và y.
Cũng trong bài viết trước BigDataUni đã giới thiệu đến các bạn phương pháp kiểm định kết quả của phân tích tương quan. Trong bài viết tiếp theo tổng quan về hồi quy, chúng ta sẽ tìm hiểu về các phương pháp kiểm định áp dụng cho Simple linear regression, nhưng trước hết chúng ta sẽ xem qua mối liên hệ giữa hệ số tương quan và hệ số hồi quy và phương pháp kiểm định cho Correlation như một cách review lại kiến thức cũ. Các bạn có thể tham khảo chi tiết bài viết trước trong link dưới đây: Tổng quan về Correlation và Simple linear regression (chèn link vô sau) Kiểm định giả thuyết (Hypothesis Test) là một trong những kiến thức nền tảng, và quan trọng nhất trong lĩnh vực thống kê (Statistics), được sử dụng để đánh giá liệu các giả thuyết từ dữ liệu mẫu có thể suy ra dữ liệu tổng thể nghiên cứu được hay không. Nói cách khác dựa trên các tham số, đặc trưng của mẫu, các kết luận đưa ra về quy luật phân phối, các đặc trưng của tổng thể có hợp lý hay không.
Để tìm hiểu kiểm định là gì, các bạn cũng có thể xem qua bài viết BigDataUni trong link dưới đây: Tổng quan về Statistics: Inferential statistics (thống kê suy luận)
Mối liên hệ giữa hệ số hồi quy và hệ số tương quan
Quay trở lại với chủ đề bài viết, đầu tiên là Correlation. Nhắc lại công thức tính hệ số tương quan, và cách giải thích mối quan hệ giữa 2 biến dựa trên hệ số tương quan:
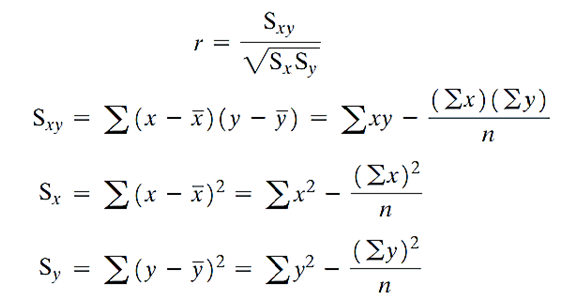
Công thức trên (n – 1) đã bị triệt tiêu. Theo lý thuyết rxy nằm từ -1 đến +1
- Nếu hệ số rxy < 0, thì 2 biến có mối quan hệ theo chiều nghịch nhau, tức một biến tăng thì biến còn lại sẽ giảm hoặc ngược lại.
- Hệ số rxy > 0 thì 2 biến có mối quan hệ thuận, một biến tăng, biến còn lại có thể tăng theo hoặc ngược lại.
- Hệ số rxy = 0, thì 2 biến không có mối quan hệ tuyến tính với nhau.
- Hệ số rxy càng tiến gần giá trị -1, mối liên hệ nghịch càng chắc chắn, tương tự với giá trị 1, mối liên hệ thuận càng chắc chắn.
Có một lưu ý mà chúng tôi chưa đề cập đó chính là sự liên hệ giữa hệ số tương quan r và hệ số đường hồi quy β1
Cả hệ số tương quan r và hệ số đường hồi quy β1 đều có thể mô tả mối quan hệ giữa 2 biến x và y bất kỳ. Với r chúng ta biết được nếu x tăng hay giảm thì y sẽ thay đổi theo chiều hướng thuận, hay nghịch và sự thay đổi này có bền vững hay không, có được khẳng định chắc chắn hay không. Lấy lại ví dụ bài viết trước xem xét mối quan hệ giữa số chiến dịch quảng cáo Facebook được thực hiện trong mỗi tuần, lấy mẫu 10 tuần, và doanh thu thu nhận được mỗi tuần
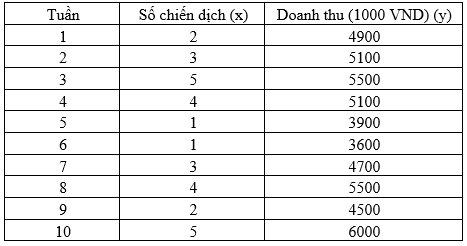
Áp dụng công thức chúng ta tính được hệ số tương quan r = 0.92, qua đó khẳng định số chiến dịch quảng cáo Facebook trong 1 tuần sẽ có tác động làm tăng doanh thu, mối quan hệ giữa 2 biến là mối quan hệ thuận chiều, và bền vững. Tuy nhiên bây giờ chúng ta muốn biết khi tăng 1 chiến dịch quảng cáo Facebook trong 1 tuần thì doanh thu sẽ tăng lên bao nhiêu trong chính tuần này, thì phải làm cách nào? Chúng ta sẽ dùng hệ số đường hồi quy β1 để xác định. Phương trình tổng quát của mô hình hồi quy tuyến tính đơn giản:
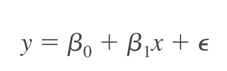
Phương trình hồi quy tổng quát áp dụng cho ví dụ trên:
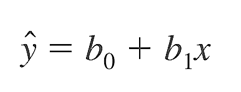
Nhắc lại, β0 là giá trị ước lượng của y khi x đạt giá trị 0 (Intercept), β1 là độ dốc của đường hồi quy tuyến tính (Slope), nói cách khác là mức độ thay đổi của y khi x thay đổi 1 đơn vị, ε là sai số, thể hiện giá trị của các yếu tố khác không thể nghiên cứu hết và các yếu tố này vẫn tác động lên giá trị của y
Công thức tính hệ số hồi quy b1 và giá trị b0
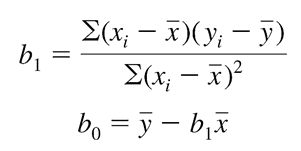
Chúng ta áp dụng cho ví dụ trên để tính b1 và b0, kết quả các bạn sẽ có phương trình như sau:
b1 = 9200/20 = 460
b0 = 4880 – 460*3 = 3500 với 4880 là doanh thu trung bình, 3 là số chiến dịch trung bình mỗi tuần.
Phương trình hồi quy tuyến tính xây dựng được: y^ = 3500 + 460x Với b1 = 460, giá trị dương, chúng ta có thể kết luận nếu trong tuần tăng trung bình 1 chiến dịch quảng cáo Facebook thì doanh thu trung bình sẽ tăng 460 (1000 VND)
Như vậy chúng ta đã thấy được sự khác biệt giữa r và b1 trong cách thể hiện mối quan hệ giữa 2 biến tuy nhiên câu hỏi tiếp theo đặt ra. Tại sao chúng ta cần hệ số tương quan trong khi đã có hệ số hồi quy định lượng rõ ràng hơn mối quan hệ giữa 2 biến? Nói cách khác thay vì sử dụng hệ số tương quan, chúng ta có thể sử dụng hệ số hồi quy để xem xét tính bền vững trong quan hệ giữa 2 biến hay không?
Câu trả lời là không thể. Hệ số hồi quy phụ thuộc vào đơn vị đo lường của biến mục tiêu y, và không có một giới hạn giá trị dự báo cụ thể tức hệ số hồi quy có thể rất cao cũng có thể rất thấp, cũng có thể rất lớn và rất nhỏ. Ví dụ ở trên khi b1 = 460 các bạn có thể khẳng định đây là mối quan hệ bền vững hay không? Cơ sở nào để khẳng định? Nhưng nếu so sánh với các tập dữ liệu khác nhau chúng ta có thể sử dụng hệ số hồi quy để khẳng định tính bền vững. Ví dụ nếu không sử dụng chiến dịch quảng cáo thì công ty có thể sử dụng chính sách giảm giá trong những giờ cao điểm, vậy giả sử hệ số b1 = 600, chứng tỏ chính sách giảm giá có tác động mạnh hơn lên doanh thu trung bình, tuy nhiên chúng ta vẫn chưa xét đến b0 nên lại không thể khẳng định giá trị dự báo cho doanh thu của bên nào là lớn hơn
Hệ số tương quan r phù hợp hơn khi đánh giá tính bền vững trong mối quan hệ giữa 2 biến vì r được giới hạn từ -1 đến 1, giá trị càng tiến gần 2 điểm giới hạn này thì mối quan hệ càng bền vững bất kể thuận hay nghịch, không quan tâm đến đơn vị đo lường của x và y. Trong công thức của hệ số tương quan có chung một thành phần trong công thức của hệ số hồi quy, và thực tế trên cơ sở tính toán, nếu hệ số hồi quy bằng 0 thì hệ số tương quan cũng sẽ bằng 0 – trường hợp biến x không có liên hệ hay đóng góp gì trong quá trình dự báo giá trị y, nếu hệ số tương quan có giá trị dương thì hệ số hồi quy cũng sẽ có giá trị dương và ngược lại. Hai lưu ý cực kỳ quan trọng chúng tôi muốn lưu ý đến các bạn lại không đề cập trong bài viết trước chính là:
- Hệ số tương quan cao không thể hiện mối quan hệ nhân quả hoàn toàn giữa x và y
- Hệ số tương quan thấp không có nghĩa x và y không có mối liên hệ, chỉ là mối quan hệ tuyến tính không mạnh mà thôi.
Nói tóm lại, hệ số tương quan r chính là hệ số hồi quy được chuẩn hóa (Standardized Slope), mối liên hệ giữa chúng được thể hiện qua công thức dưới đây:
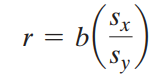
Hệ số tương quan sẽ bằng hệ số hồi quy khi Sx = Sy, và vì lý do hệ số tương quan không bị ảnh hưởng bởi đơn vị đo lường của các biến nên chúng ta có thể chuẩn hóa giá trị của biến x và y, sử dụng công thức chuẩn hóa Z – score, chúng ta vẫn sẽ tính được tương tự hệ số r. Như vậy trên cơ sở hệ số tương quan là hệ số chuẩn hóa của b, chúng ta có thể kết luận nếu giá trị chuẩn hóa Z của x thay đổi 1 đơn vị thì giá trị chuẩn hóa của Z của y sẽ thay đổi r đơn vị.
Như vậy, với lập luận trên chúng ta đang khẳng định ngược lại với lý thuyết trong bài viết trước và ở chính trong bài viết này về hệ số tương quan đó chính là: hệ số tương quan không lượng hóa được mối quan hệ giữa biến x và y, nhưng với giá trị được chuẩn hóa thì chúng ta có thể. Công thức chuẩn hóa giá trị lấy ví dụ cho biến x dành cho những bạn chưa biết:
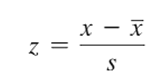
Như vậy chúng ta đã tìm hiểu xong mối liên hệ giữa hệ số tương quan và hệ số hồi quy. Tiếp theo chúng ta cùng làm quen với các phương pháp kiểm định cho phân tích tương quan và hồi quy tuyến tính đơn giản.
Phương pháp kiểm định trong Correlation
(Phần này chúng tôi đã trình bày trong bài viết trước, lần này chúng tôi chỉ làm rõ hơn một số vấn đề, lưu ý thêm các bạn phải có kiến thức cơ bản về kiểm định vd như mức ý nghĩa, p-value)
Tại sao phải thực hiện kiểm định trong phân tích tương quan? Đó chính là do chúng ta muốn tìm hiểu xem liệu các kết luận ở mẫu có thể áp dụng cho toàn bộ tổng thể nghiên cứu hay không? Ở ví dụ trên chúng ta tính được r = 0.92, và kết luận rằng các chiến dịch quảng cáo có thể làm tăng doanh thu. Tuy nhiên chúng ta chỉ lấy có 10 tuần để đánh giá, giả sử nếu muốn xem xét trong cả năm vừa rồi thậm chí từ lúc công ty bắt đầu chạy chiến dịch quảng cáo, chúng ta có thể kết luận tương tự như trên được không? Phương pháp kiểm định trong thống kê là công cụ hữu ích để giải quyết vấn đề này.
Ở bài viết trước chúng tôi đã đề cập đến các bạn công thức tính giá trị kiểm định t cho hệ số tương quan r để bác bỏ hay không bác bỏ giả thuyết có mối tương quan giữa 2 biến.
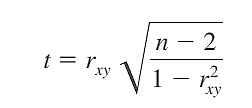
pxy là hệ số tương quan của tổng thể, chúng ta có các giả thuyết H0 như sau:
H0: pxy = 0 H0: pxy ≤ 0 H0: pxy ≥ 0
H1: pxy ≠ 0 H1: pxy > 0 H1: pxy < 0
Pxy > 0, trong tổng thể, x và y có mối quan hệ thuận, Pxy < 0 , trong tổng thể, x và y có mối quan hệ nghịch, Pxy = 0, trong tổng thể, x và y không có mối quan hệ. Chúng ta sẽ tính toán giá trị kiểm định t và so sánh với t tra bảng, với mức ý nghĩa α, và bậc tự do n – 2, H0: pxy = 0 là kiểm định 2 phía, mức ý nghĩa α được chia 2 khi tra bảng, còn lại là kiểm định 1 phía và mức ý nghĩa α được giữ nguyên khi tra bảng.
Cơ sở bác bỏ H0
Với kiểm định 2 phía: H0: pxy = 0 được bác bỏ khi trị tuyệt đối của t lớn hơn t tra bảng (tα/2, n-2)
Với kiểm định bên phải: H0: pxy ≤ 0 được bác bỏ khi giá trị t dương lớn hơn giá trị dương của t tra bảng (tα, n-2)
Với kiểm định bên trái: H0: pxy ≥ 0 được bác bỏ khi giá trị t < giá trị âm của t tra bảng (tα, n-2)
Nếu xét trên giá trị p-value, bác bỏ H0 khi p-value < α. (p-value là mức ý nghĩa nhỏ nhất mà tại đó H0 bị bác bỏ)
Chúng ta sử dụng lại ví dụ trên để tính với r = 0.92 và được t = 6.8 Chúng ta sẽ tra bảng phân phối t để tìm t(α), n-2 với mức ý nghĩa α là 0.05 (độ tin cậy 95%), bậc tự do n – 2 là 10 – 2 =8, vì là kiểm định 1 bên nên chúng ta giữ nguyên α.
Các bạn có thể search trên Google để kiếm thông tin về bảng phân phối t để tra, ở đây chúng tôi đã tra sẵn t0.05, 8 = 1.86. Như vậy t = 6.8 lớn hơn t tra bảng vậy chúng ta bác bỏ H0 và khẳng định có mối liên hệ thuận giữa 2 biến. Ngoài ra các bạn có thể sử dụng p-value để xem xét bác bỏ H0 nếu p-value < α.
Các bạn có thể tra ngược lại bảng t với giá trị là 6.8 thì đối chiếu lên hàng trên cùng là giá trị bao nhiêu hoặc có thể sử dụng hàm T.DIST.RT (vì ở đây ta kiểm định 1 phía bên phải, RT – Right tailed) trong excel nhập 6.8 và bậc tự do là 8.
Tuy nhiên một lưu ý quan trọng không chỉ trong phương pháp kiểm định trong Correlation mà còn ở những phương pháp kiểm định khác đó chính là giá trị kiểm định chỉ cho chúng ta biết được liệu giả thuyết về tổng thể có được chấp nhận hay không, nếu được hay không được, thì nó mới chỉ là thông tin, hay ý kiến mà chúng ta có thể xem xét chứ không được dựa hoàn toàn mà đưa ra một quyết định cụ thể, phải cân nhắc rất nhiều yếu tố khác.
Như chúng tôi đã đề cập hệ số tương quan cao hay không thấp không thể hiện hoàn toàn mối quan hệ nhân quả giữa 2 biến, ví dụ r = 0.92, chúng ta không thể 100% kết luận các chiến dịch quảng cáo sẽ làm tăng doanh thu mà phải thực hiện kiểm định hay lập phương trình hồi quy. Hay giả sử nếu thông kiểm định, giả thuyết doanh thu và chiến dịch quảng cáo có mối quan hệ thuận chiều bị bác bỏ, chúng ta vội vàng cho rằng chiến dịch quảng cáo không hiệu quả, không làm tăng doanh thu và loại bỏ phương pháp marketing này, không đầu tư nữa.
Đây là sai lầm! Chiến dịch quảng cáo Facebook không hiệu quả có thể đến từ nhiều nguyên nhân khác nhau mà chúng ta chưa rà soát hết, từ chính các thuật toán Facebook triển khai để tối ưu trải nghiệm người dùng cho đến các nội dung quảng cáo không thực sự thu hút hay phù hợp với người dùng.
Nói tóm lại, kết quả của phương pháp kiểm định chỉ nên là thông tin tham khảo chứ không phải yếu tố then chốt để chúng ta ra quyết định.
Phương pháp kiểm định trong Simple linear regression
Khi thực hiện phân tích hồi quy, và thiết lập phương trình hồi quy, chúng ta sẽ đưa ra những giả định phù hợp về mối quan hệ giữa 2 biến phụ thuộc và độc lập, và những giả định này sẽ dựa trên phương trình tổng quát:
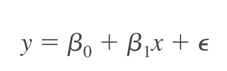
Phương pháp bình phương bé nhất sẽ cho chúng ta tính toán được các giá trị b0 và b1, những giá trị này sẽ được dùng để ước lượng cho β0 và β1. Kết quả chúng ta sẽ có được phương trình hồi quy ước lượng:
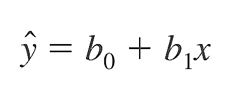
Chúng ta có hệ số xác định r2 (Coefficient of Determination) để đánh giá mức độ phù hợp của mô hình hay phương trình trong việc giải thích mối quan hệ giữa x và y.
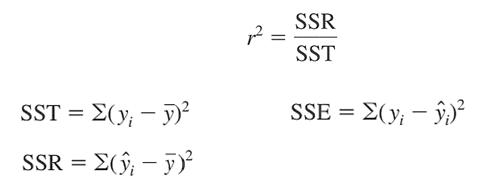
(SST thể hiện toàn bộ phần biến thiên của các giá trị y so với trung bình của nó. SSR thể hiện phần chênh lệch giữa giá trị dự báo so với trung bình, được hiểu là sự biến thiên của y mà chúng ta có thể giải thích được bằng biến x, và SSE là thể hiện phần chênh lệch giữa giá trị thực tế và giá trị dự báo, không thể giải thích được nguyên nhân)
Tuy nhiên cho dù hệ số xác định có lớn như thế nào thì chúng ta không thể lấy phương trình hồi quy ước lượng để dùng cho chính phương trình hồi quy tổng quát, chúng ta phải thực hiện nhiều phương pháp khác nhau để đánh giá chi tiết hơn mức độ phù hợp, trong đó có phương pháp kiểm định. Phương pháp kiểm định đối với phân tích hồi quy phải dựa trên những giả định về sai số ε của phương trình hồi quy tổng quát. Nhắc lại, ε là sai số, thể hiện giá trị của các yếu tố khác không thể nghiên cứu hết và các yếu tố này vẫn tác động lên giá trị của y.
- ε là một biến ngẫu nhiên có phân phối chuẩn với trung bình và giá trị kỳ vọng bằng 0: E(ε) = 0
- ε có phương sai ký hiệu σ2 bằng nhau với mọi giá trị x.
- Các giá trị ε là độc lập, không có mối quan hệ với nhau
Trong phương trình hồi quy tuyến tính đơn giản, giá trị trung bình hay giá trị kỳ vọng của y phụ thuộc x sẽ là: E(y) = β0 + β1x. Nếu β1 = 0, E(y) = β0 lúc này y không có quan hệ tuyến tính với biến x, ngược lại với β1 khác 0. Chúng ta phải thực hiện kiểm định để kiểm tra xem liệu hệ số β1 có khác 0 hay không. Có 2 phương pháp kiểm định chính đó là kiểm định t và kiểm định F, cả 2 đều dựa trên việc ước lượng phương sai σ2 của sai số ε. Để uớc lượng phương sai σ2 của sai số ε, chúng ta sẽ sử dụng giá trị SSE, phần chênh lệch giữa giá trị thực tế và giá trị dự báo, không thể giải thích được nguyên nhân, tức ở đây chúng ta sẽ tính toán tổng chênh lệch bình phương giữa giá trị thực tế và giá trị dự báo. Giá trị ước lượng σ2 của sai số ε sẽ bằng SSE chia cho n – 2 là bậc tự do, được gọi là s2 hay se2 .
Giá trị ước lượng sau khi tính toán còn được gọi là MSE (Mean Square Error) – trung bình bình phương sai số dự báo, đây còn được coi là thước đo trong việc đánh giá mô hình hồi quy có hiệu quả trong việc dự báo hay không. Công thức tổng quát sau cùng:
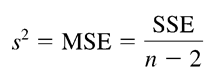
Tiếp theo chúng ta sẽ tính sai số chuẩn của sai số ε (standard error of the estimate) bằng cách khai căn bậc 2 của phương sai được ước lượng:
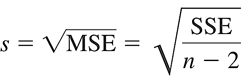
Chúng ta đi vào phương pháp kiểm định đầu tiên. t – test, kiểm định t Chúng ta có thể đặt các giả thuyết như sau, tùy theo mục đích kiểm định:
H0: β1 = 0 H0: β1 ≤ 0 H0: β1 ≥ 0
H1: β1 ≠ 0 H1: β1 > 0 H1: β1 < 0
Tuy nhiên để kiểm định cho giá trị β1 cho tổng thể chúng ta phải dựa vào giá trị b1 tìm được từ bộ dữ liệu mẫu, do đó chúng ta phải xem xét phân phối mẫu của b1 có đủ điều kiện để thực hiện kiểm định hay không. Phân phối mẫu của b1 có các tính chất như sau:
- Giá trị kỳ vọng E(b1) = β1
- Độ lệch chuẩn:
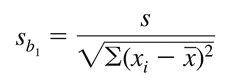
- Phân phối của mẫu thuộc dạng phân phối chuẩn
Như vậy sau cùng chúng ta có công thức tổng quát của giá trị kiểm định t như sau:
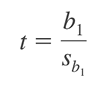
Nguyên tắc bác bỏ H0: Với kiểm định 2 phía: H0: β1 = 0 được bác bỏ khi trị tuyệt đối của t lớn hơn t tra bảng (tα/2, n-2) Với kiểm định bên phải: H0: β1 ≤ 0 được bác bỏ khi giá trị t dương lớn hơn giá trị dương của t tra bảng (tα, n-2)
Với kiểm định bên trái: H0: β1 ≥ 0 được bác bỏ khi giá trị t < giá trị âm của t tra bảng (tα, n-2) Nếu xét trên giá trị p-value, bác bỏ H0 khi p-value < α. (p-value là mức ý nghĩa nhỏ nhất mà tại đó H0 bị bác bỏ). Chúng ta cùng đi qua dạng kiểm định thứ 2 F – test, kiểm định F
Tương tự như kiểm định t, kiểm định F, dựa trên phân phối F – một dạng phân phối xác suất, cũng sẽ xác định bác bỏ hay không bác bỏ giả thuyết H0: β1 = 0. Tuy nhiên khác với kiểm định t, kiểm định F có thể kết luận có hay không có mối quan hệ tuyến tính giữa một biến phụ thuộc y và nhiều biến độc lập x một cách tổng quát.
Chúng tôi sẽ trình bày trường hợp này kỹ hơn trong bài viết sắp tới về Hồi quy tuyến tính đa biến (bội).
Multiple linear regression, còn trong bài viết này chúng ta chỉ quan tâm trường hợp một biến x mà thôi. Kiểm định F ngoài sử dụng MSE, ước lượng phương sai của sai số, mà còn sử dụng thêm.
MSR(mean square regression) được tính bằng cách lấy SSR chia cho bậc tự do của phương trình hồi quy, là số biến độc lập có trong phương trình, ở đây chúng ta chỉ có 1 biến x nên bậc tự so bằng 1. MSR chính là giá trị ước lượng phương sai σ2 dựa trên SSR.
Lưu ý, kiểm định F cho hệ số hồi quy β1 chủ yếu là kiểm định 1 phía, sử dụng mức ý nghĩa α cho trước. Công thức tổng quát của giá trị kiểm định F là:
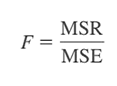
Cơ sở bác bỏ H0:
- p – value nhỏ hơn mức ý nghĩa α
- giá trị F tính được phải lớn hơn giá trị F tra bảng phân phối F (với bậc tự do thứ nhất là 1 ở hàng trên cùng, và bậc tự do thứ hai là n – 2 ở cột ngoài cùng, α ở cột thứ 2 tính từ cột ngoài cùng)
Chúng ta có bảng ANOVA (phân tích phương sai) tổng quát như sau.
Phương pháp phân tích phương sai (Analysis of Variance) chúng tôi sẽ trình bày ở những bài viết sắp tới, cũng lưu ý thêm kiểm định F là phương pháp phân tích ANOVA để tìm hiểu mối quan hệ giữa 2 biến x và y dựa trên phương trình hồi quy.
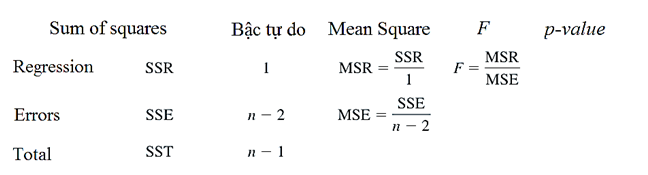
Triển khai kiểm đinh t và kiểm định F cho ví dụ cụ thể
Chúng ta lấy lại ví dụ thứ 2 của bài viết trước để thực hiện kiểm định. Giá sử một chuỗi cửa hàng gà rán có 10 cửa hàng nằm tại các quận khác nhau trên thành phố Hồ Chí Minh, tại từng khu vực của từng cửa hàng sẽ có số lượng học sinh, sinh viên sinh sống và học tập, chuỗi cửa hàng này muốn biết rằng doanh thu của từng cửa hàng có mối liên hệ nào với số lượng học sinh, sinh viên này không (dựa trên dữ liệu doanh thu trung bình theo quý của mỗi cửa hàng, và dữ liệu thống kê về số lượng học sinh, sinh viên)
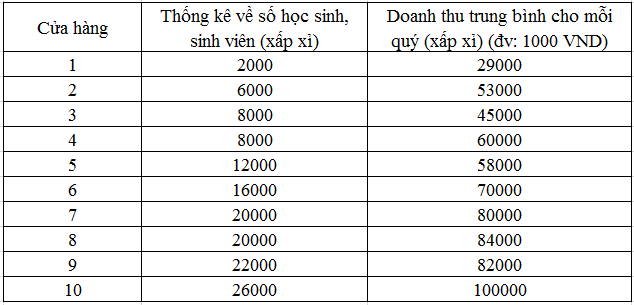
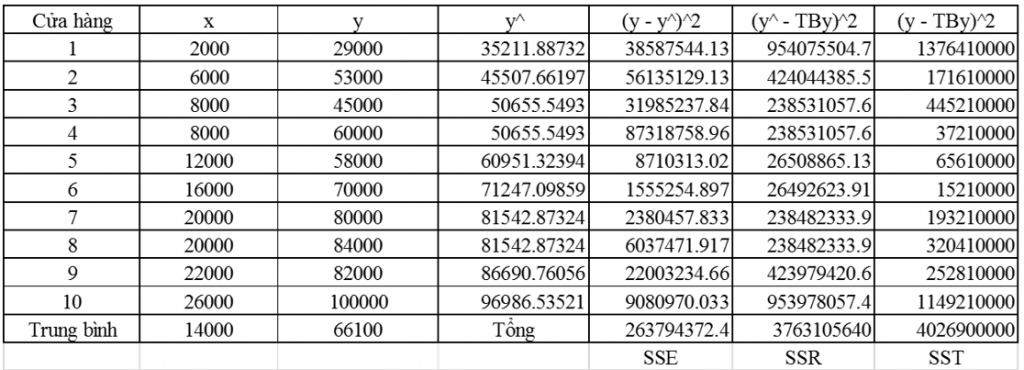
Gọi x là số lượng HS, SV, y là doanh thu, là biến mục tiêu dự báo, chúng ta sẽ sử dụng công thức tính bo và b1 để lập phương trình, chúng ta tính được trung bình x: TBx = 14000, trung bình của y: TBy = 66100 Với b1 = 2.57. Với số lượng HS, SV tăng 1000 thì doanh thu của 1 cửa hàng sẽ tăng 2570000 VND, và b0 = 30064. (Cách tính toán các hệ số hồi quy và lập phương trình các bạn vui lòng xem lại bài viết trước) Chúng ta có phương trình hồi quy tuyến tính đơn giản: Y^ = 2.57X + 30064.
Chúng ta thay từng giá trị x vào phương trình mới tìm được để tính giá trị Y^ dự báo, sau đó tính SSE, SSR dựa trên Y^.
Đặt giả thuyết:
H0: β1 = 0 : Không có mối quan hệ giữa số HS, SV và doanh thu mỗi cửa hàng
H1: β1 ≠ 0 Có mối quan hệ giữa số HS, SV và doanh thu mỗi cửa hàng
Các bạn áp dụng trình tự theo công thức chúng tôi trình bày ở trên.
Kiểm định t: S = căn bậc 2 (SSE/n – 2) = căn bậc 2 (263794372.4/8) = 5742.3 Sb = S/(căn bậc 2 của Sx) = 5742.3/(căn bậc 2 (568000000)) = 0.24 t = b/Sb = 2.57/0.24 = 10.7
t tra bảng với mức ý nghĩa α = 5%, bậc tự do là 8, tα/2,8 = 2.306
Như vậy với t > tα/2,8, chúng ta bác bỏ giả thuyết H0, tức có mối quan hệ giữa 2 biến số lượng học sinh sinh viên trong khu vực và doanh thu của mỗi nhà hàng trong khu vực ấy. Tương tự giá trị p-value = 0.000005 tính được nhỏ hơn rất nhiều so với mức ý nghĩa, nên chúng ta bác bỏ H0.
Các bạn có thể dùng hàm T.DIST trong excel để tìm p-value. Còn với kiểm định F: MSE = SSE/(n – 2) = 263794372.4/8 = 32974295.77 MSR = SSR/1 = 3763105640 F = MSR/MSE = 114 F tra bảng với mức ý nghĩa 5%, Fα,1,8 = 5.32 F > Fα,1,8, chúng ta bác bỏ H0 và kết luận tương tự như trên. Bảng ANOVA có được:

Significance F là p-value, các bạn cũng có thể sử dụng hàm F.DIST trong excel để tính.
Các lý thuyết trong bài viết được tham khảo và kiểm chứng từ những tài liệu quốc tế về lĩnh vực thống kê Statistics: The Art and Science of Learning from Data” (4th Global Edition 2018) của nhà xuất bản Pearson, “Basic Statistics for Business and Economics” (9th Edition 2019) của nhà xuất bản Mc Graw Hill, “Statistics for Business and Economics” (13th Edition 2017) của Cengage Learning)
Như vậy chúng ta đã tìm hiểu xong các phương pháp kiểm định trong hồi quy tuyến tính đơn giản. Ở bài viết tới chúng ta sẽ đi vào tìm hiểu mô hình hồi quy tuyến tính đa biến – Multiple linear regression. Mong các bạn tiếp tục ủng hộ BigDataUni.
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English