Ở các phần trước trong chủ đề về Statistics (thống kê) BigDataUni đã giới thiệu đến các bạn các khái niệm, lợi ích, ứng dụng của thống kê, đặc biệt Descriptive statistics (thống kê mô tả), một trong 2 dạng cơ bản của Statistics.
Trở lại với bài viết lần này chúng tôi sẽ trình bày tóm tắt về dạng còn lại, chính là một số kiến thức của Inferential Statistics hay còn gọi là thống kê suy luận.
Tổng quan về Statistics: Descriptive statistics (Thống kê mô tả)
Nhắc lại một chút về định nghĩa, Inferential Statistics (Statistical Inference), thống kê suy luận bao gồm nhiều những phương pháp như ước lượng, đưa ra các giả thuyết và kiểm định giả thuyết, phân tích mối tương quan, liên hệ giữa các đối tượng nghiên cứu, đưa ra các dự báo, trên cơ sở phân tích dữ liệu mẫu để tìm ra những hiểu biết, đặc điểm về tổng thể.
Thông thường trong thực tế lý do sử dụng thống kê suy luận khi tiến hành một dự án nghiên cứu nào đó, chúng ta không thể thu thập tất cả các đơn vị trong một tổng thể, hoặc một tổng thể chúng ta quan tâm có rất nhiều đơn vị, nhiều quan sát khiến cho việc thu thập mất nhiều thời gian, tốn kém. Dưới đây là trường hợp để minh họa cho các bạn rõ hơn: Giả sử một công ty muốn nghiên cứu về mức độ hài lòng của khách hàng về sản phẩm mới trại thị trường thành phố Hồ Chí Minh, công ty này sẽ khảo sát một lượng khách hàng nhất định ở mỗi quận, huyện, nơi sản phẩm của họ được tiêu thụ, và có được một bộ dữ liệu mẫu từ tổng thể, nếu trường hợp công ty này không có hệ thống thu thập dữ liệu, không có đủ điều kiện, năng lực về mặt nền tảng công nghệ, tài chính để tiến hành khảo sát tổng thể trên toàn thị trường, và phải thực hiện thống kê suy luận.
Đây là trường hợp phổ biến hơn trường hợp tiếp theo dưới đây. Nếu ngược lại, công ty có khả năng theo dõi hành vi tiêu dùng, có một quy trình thu thập dữ liệu cụ thể là thông tin cá nhân, và feedback (phản hồi) từ khách hàng, có hệ thống lưu trữ, quản lý dữ liệu tối ưu, thì dữ liệu họ có được có thể là dữ liệu tổng thể nghiên cứu mà họ mong muốn.
Tuy nhiên để phục vụ giai đoạn phân tích nhằm tìm ra những thông tin hữu ích một cách nhanh chóng ví dụ để sớm giải quyết những vấn đề từ sản phẩm mới mà khách hàng phản ánh, các chuyên gia không thể dành toàn bộ thời gian phân tích hết dữ liệu tổng thể chưa nói đến quá trình xử lý dữ liệu ban đầu, đặc biệt là khâu chuẩn bị dữ liệu thông thường chiếm gần 80% thời gian, sẽ khiến họ chậm tiến độ.
Vì vậy, họ cũng cần chọn lọc và lấy ra một lượng dữ liệu từ dữ liệu tổng thể làm dữ liệu mẫu để tiến hành phân tích. Trường hợp này thực chất rất ít khi xảy ra trong bối cảnh ngày nay, do thông thường nếu một công ty đã có cho mình hệ thống thu thập, lưu trữ, quản lý dữ liệu thì cũng đã xây dựng các quy trình khai thác dữ liệu hiệu quả, áp dụng các công cụ, nền tảng công nghệ tiên tiến có thể phân tích khối lượng lớn dữ liệu trong thời gian ngắn. Chắc chắn trong chúng ta sẽ có hoài nghi liệu rằng nếu chỉ dựa trên dữ liệu mẫu, những thông tin chúng ta có được khi phân tích, có áp dụng được cho tổng thể nghiên cứu hay không? Nói cách khác, dữ liệu mẫu có nói cho chúng ta biết chính xác những gì về tổng thể hay không? Những kết luận từ dữ liệu mẫu nếu áp dụng kết luận cho tổng thể thì độ chính xác, tin cậy là bao nhiêu?
May mắn thay, chúng ta có đầy đủ khả năng trả lời những câu hỏi, giải đáp những hoài nghi trên dựa vào thống kê suy luận (Inferential statistics). Thống kê suy luận cung cấp các phương pháp giúp chúng ta đi sâu vào phân tích các đối tượng trong bộ dữ liệu mẫu không chỉ dừng lại ở thống kê mô tả, đưa ra những phán đoán có cơ sở, có độ tin cậy nhất định để từ đó thiết lập các kết luận chính xác về tổng thể nghiên cứu. Trở lại với ví dụ trên, các bạn có thắc mắc như trường hợp 1: nếu công ty không thể khảo sát hết tất cả các quận huyện những nơi sản phẩm mới được tiêu thụ thì họ phải chọn ra những quận, huyện nào để khảo sát với cách thức như thế nào? Số lượng khách hàng được khảo sát (phạm vi đơn vị mẫu) là bao nhiêu, tỷ lệ như thế nào?
Cũng như trường hợp 2, khi công ty có dữ liệu tổng thể, vậy họ sàng lọc, chọn ra các nhóm dữ liệu mẫu như thế nào để phân tích? Công ty sẽ phải dựa vào phương pháp chọn mẫu (Sampling) trong Inferential Statistics. Ở bài viết lần này, chúng tôi chỉ đề cập tổng quan đến một số cách thức chọn mẫu chứ không trình bày cụ thể về những công thức tính toán như xác định cỡ mẫu, sai số,v.v. Tiếp theo trong thống kê suy luận, BigDataUni sẽ cung cấp tóm tắt những kiến thức cơ bản mà các bạn cần phải nắm:
- Một số quy luật phân phối xác suất thông dụng (Probability Distributions)
- Phân phối mẫu (Sampling Distributions) – phân phối trung bình mẫu
- Ước lượng (Estimation)
- Kiểm định giả thuyết (Hypothesis Tests)
Những kiến thức quan trọng cần nắm trong thống kê suy luậnSampling (chọn mẫu) Quá trình chọn mẫu bao gồm những phương pháp phổ biến sau:
Chọn mẫu ngẫu nhiên đơn giản (Simple random sample):
Là phương pháp phổ biến nhất, lấy mẫu từ một tổng thể hữu hạn, tức chúng ta phải có được thông tin về toàn bộ các đơn vị trong tổng thể ví dụ như có một tập dữ liệu, một bảng dữ liệu chứa 2 triệu đơn vị (hay records) có đánh số thứ tự từng đơn vị. Các đơn vị mẫu được rút ra một cách ngẫu nhiên (dùng cách rút thăm, quay số, hoặc bảng số ngẫu nhiên) sao cho mỗi một mẫu có kích thước n được rút ra từ tổng thể có kich thước N sẽ có xác suất xảy ra (xác suất được chọn) như nhau.
Chọn mẫu ngẫu nhiên (Random sample):
Trường hợp tổng thể rất nhiều đơn vị mà chúng ta không thể nào xác định hết được, lúc này các chuyên gia thống kê đề xuất phương pháp chọn mẫu ngẫu nhiên, nghĩa là chọn ra các đơn vị mẫu sao cho thỏa 2 điều kiện: 1) mỗi đơn vị mẫu đều thuộc tổng thể nghiên cứu. 2) mỗi đơn vị mẫu được chọn một cách độc lập. Lấy mẫu hệ thống (Systematic Sampling): các đơn vị của tổng thể được sắp xếp từ 1 đến N với N là tổng các đơn vị tổng thể, lúc này chúng ta lấy ra n đơn vị mẫu với k = N/n là khoảng cách chọn mẫu, nghĩa là cứ cách k đơn vị thì ta chọn một đơn vị đưa vào mẫu từ vị trí ngẫu nhiên (đơn vị mẫu đầu tiên được chọn).
Lấy mẫu ngẫu nhiên phân tầng (Stratified Random Sampling):
Tổng thể gồm N đơn vị sẽ được chia thành các nhóm, mỗi nhóm sẽ có chứa số đơn vị tổng thể nhất định. Các đơn vị mẫu sau đó sẽ được chọn ra ngẫu nhiên từ các nhóm này. Chọn mẫu cụm (Clustering sampling): là phương pháp mà tổng thể được chia thành các khối, các cụm trước sau các các đơn vị mẫu được chọn ra theo từng khối, từng cụm chứ không phải chọn ra từng đơn vị riêng, lẻ tẻ. Ví dụ khảo sát khách hàng ở quận 1, quận 3, quận Bình Thạnh, thì giả sử số khách hàng được khảo sát ở quận Bình Thạnh là 200 tức là số đơn vị mẫu là 200 ở cụm là quận Bình Thạnh, tương tự giả sử như quận 1 có 300, quận 3 có 150 đơn vị mẫu.
Chọn mẫu phi ngẫu nhiên (Non-random sampling):
Là chọn mẫu trên cơ sở xem xét chủ quan của chuyên gia phân tích, chuyên gia thống kê bao gồm chọn mẫu thuận tiện, chọn mẫu theo phán đoán và chọn mẫu theo định mức đặt ra ban đầu. Các quy luật phân phối xác suất (Probability distributions) trong thống kê suy luận Xác suất (Probability) không còn là thuật ngữ xa lạ gì đối với các bạn vì đây là kiến thức toán quan trọng trong trung học phổ thông và ở đại học, là kiến thức cốt lõi của thống kê.
Chính vì vậy trong bài viết này chúng tôi sẽ không giới thiệu lại những công thức xác suất cơ bản, mà chỉ trình bày các quy luật phân phối xác suất thông dụng. Xác suất hiểu đơn giản là một thước đo, định lượng khả năng xảy ra của một sự kiện nào đó. Xác suất luôn được giới hạn trong giá trị từ 0 đến 1, xác suất càng gần 0 thì khả năng xảy ra sự kiện đó ngày càng thấp, và ngược lại.
Để xác định các đại lượng ngẫu nhiên, chúng ta phải biết được mỗi một đại lượng ngẫu nhiên có thể nhận giá trị nào trong một tập hợp các giá trị, với xác suất tương ứng là bao nhiêu, đây chính là cách chúng ta đang xem xét đến phân phối xác suất cho từng giá trị có thể xảy ra. Các quy luật phân phối xác suất được thiết lập và áp dụng cho 2 loại đại lượng ngẫu nhiên rời rạc (Discrete probability distributions), và đại lượng ngẫu nhiên liên tục (Continuous probability distributions).
Đại lượng ngẫu nhiên có khái niệm gần giống như biến định lượng.
Đối với đại lượng ngẫu nhiên rời rạc (biến định lượng rời rạc)
Các giá trị hữu hạn có thể có là x1, x2,…,xk với các xác suất tương ứng là p1, p2,…, pk. Luật phân phối xác suất của đại lượng ngẫu nhiên rời rạc như trong bảng sau: Tổng các xác suất có thể xảy ra ứng với mỗi giá trị sẽ bằng 1. Ví dụ dễ hiệu và quen thuộc đó chính là bài toán tung xúc xắc, giả sử bạn tung xung xắc 1 lần thì số điểm bạn đạt được, thể hiện bằng số chấm ở mặt trên cùng con xúc xắc có thể là 1, 2, 3, 4, 5, 6, vậy tức có 6 giá trị mà đại lượng X có thể nhận x1 = 1,…., x6 = 6, xác xuất tương ứng p1 = 1/6,…, p6 = 1/6, tổng xác suất p1 đến p6 sẽ bằng 1
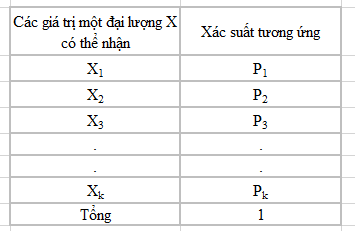
Xác suất của mỗi giá trị sẽ được tính bằng cách lấy tần số xuất hiện của giá trị đó chia cho tổng các tần số của các giá trị. pi = P(X= xi) với i = 1,2,…, k và ∑pi = 1 với pi = (fi / ∑fi) Chúng ta gọi f(x) là hàm phân phối xác suất cho các giá trị mà một đại lượng ngẫu nhiên rời rạc X có thể nhận, với mỗi giá trị f(x) bằng xác suất của mỗi giá trị x. Khi ấy phân phối xác suất cho đại lượng ngẫu nhiên rời rạc phải thỏa mãn điều kiện:

Giá trị kỳ vọng, hay trung bình giá trị mà đại lượng X có thể nhận:

Phương sai:

Ví dụ minh họa giả sử doanh số một chi nhánh của công ty bán xe ô-tô trong một ngày như sau:

Chúng ta có bảng phân phối xác suất cho số xe ô-tô bán mỗi tháng như sau: Số ngày là tần số cho giá trị x là số xe công ty bán được, ví dụ trong 30 ngày có 8 ngày mà mỗi ngày công ty bán được 2 xe:

Số xe trung bình trong tháng chi nhánh bán được: E(x) = µ = 0*0.20 + 1*0.23 + …. + 5*0.03 = 1.8 tức xấp xỉ 2 xe mỗi ngày. Tương tự theo công thức chúng ta tính được phương sai là 1.87 xe, độ lệch chuẩn sẽ là 1.36 xe.
Quy luật phân phối nhị thức (Binomial probability distribution)
Giả sử chúng ta tiến hành tung đồng xu có 2 mặt, cho dù tung bao nhiêu lần thì chúng ta cũng chỉ được 2 kết quả là mặt trên và mặt dưới của đồng xu. Tương tự như bạn thi một cuộc thi chỉ có 2 kết quả đậu và rớt, hay dự án công ty chỉ có thành công hay thất bại.
Gọi A là kết quả xảy ra (thành công) hoặc A không xảy ra (không thành công). Ở mọi phép thử xác suất để A xảy ra phải luôn bằng một hằng số p và xác suất để A không xảy ra là q = 1 – p. Chúng ta cho X là số lần A xảy ra trong n phép thử, vậy X nhận giá trị từ 0, 1, 2, …, n, và xác suất tính được theo công thức Bernoulli. Đây gọi là quy luật phân phối nhị thức ký hiệu X~B(n,p) với n là số phép thử, p là xác suất để một trong hai kết quả xảy ra. Công thức Bernoulli:

Với x = 0,1,2, …, n. và

Giá trị trung bình của X: µ = n*p Phương sai của X: σ2 = n*p*q Ví dụ trong một nhà máy sản xuất sản phẩm có tỷ lệ sản xuất ra sản phẩm lỗi (phế phẩm) là 5% theo điều tra trước đây, vậy chọn ra 20 sản phẩm thì xác suất công ty bị 5 sản phẩm lỗi là bao nhiêu? Phân phối xác suất f(5) = (20!/(5!*(20 – 5)!))*(0.05^5)*(1 – 0.05)^15 = 0.0022 với p = 0.05 và q = 1 – p = 1 – 0.05 =0.95, x = 5 và n = 20.
Quy luật phân phối Poisson (Poisson probability distribution)
Đối với trường hợp n phép thử ngày càng lớn mà xác suất p của một kết quả nào đó rất nhỏ, thì phân phối nhị thức sẽ trở nên kém hiệu quả, và việc tính toán phức tạp hơn, thì các chuyên gia thống kê sử dụng phân phối Poisson để thay thế. Đặc trưng quan trọng khác để nhận biết phân phối Poisson đó chính là nó được dùng để tính xác suất cho một sự kiện, kết quả xảy ra trong một khoảng thời gian, trong một khoảng không gian nào đó. Ví dụ số tai nạn giao thông trong một tuần ở một thành phố, hoặc số học sinh nghỉ học trong một trường học trong một ngày. Công thức phân phối Poisson như sau:
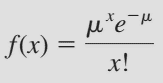
Với e là hằng số Nepe gần bằng 2.71828 µ là E(x) và là trung bình của x được tính bằng n*p Ví dụ một nhà máy sản xuất có tỷ lệ phế phẩm là 0.3%, lấy 1000 sản phẩm kiểm tra, thì xác suất tìm thấy 5 phế phẩm là bao nhiêu? n = 1000, p = 0.3% vậy µ = 1000*0.003 = 3, x = 5, e = 2.71828, đưa vào công thức chúng ta có f(x) = 0.1 là xác suất cần tìm Ví dụ khác: tại một bệnh viện, trong 1 giờ đồng hồ ở các buổi cuối tuần, ghi nhận trung bình có 6 bệnh nhân phải vào phòng cấp cứu, tính xác suất nếu có 4 bệnh nhân trong nửa giờ đồng hồ mỗi sáng thứ 7 vào phòng cấp cứu? µ = 6/2 = 3 (bệnh nhân/30 phút), x = 4 đưa vào công thức chúng ta có f(x) = 0.168 là xác suất cần tìm.
Đối với đại lượng ngẫu nhiên liên tục(biến định lượng liên tục)
Tiếp theo chúng ta đến với quy luật phân phối xác suất trong thống kê suy luận cho đại lượng ngẫu nhiên liên tục. Đối với trường hợp biến định lượng liên tục tức giá trị X lấp đầy khoảng trống của một trục số, ví dụ thu nhập, chiều cao, cân nặng của một người, v.v mà chúng ta không thể quan sát hay đếm được, thì chúng ta phải sử dụng đến quy luật phân phối chuẩn (Normal probability distribution), là quy luật phân phối quan trọng nhất của biến định lượng liên tục, và phổ biến nhất trong thống kê. Ký hiệu phân phối chuẩn: X~N (µ, σ2).
Công thức của hàm mật độ xác suất:
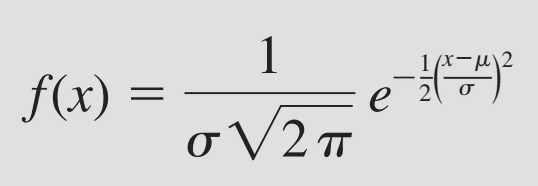
Với x nằm trong khoảng từ – ∞ và + ∞ σ là độ lệch chuẩn π = 3.14159 e = 2.71828 Đồ thị của hàm mật độ xác suất của phân phối chuẩn:
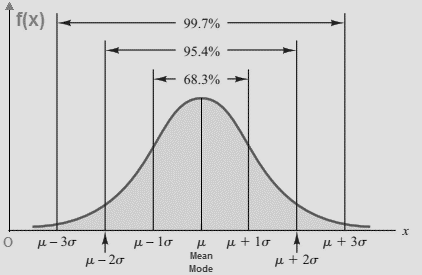
Các tính chất của phân phối chuẩn: Đồ thị của phân phối chuẩn có hình dạng giống như cái chuông được cân bằng bởi giá trị trung bình (Mean) = trung vị (Median) = Mode chia hình chuông thành 2 phần mỗi bên có diện tích bị giới hạn bởi đường cong hàm mật độ, bằng 0.5. Khoảng 68% giá trị rơi vào khoảng ( – s) và ( + s), khoảng 95% giá trị rơi vào khoảng ( – 2s) và ( + 2s), và khoảng 99.7% giá trị rơi vào khoảng ( – 3s) và ( + 3s), giống các tính chất của quy tắc thực nghiệm (Empirical Rule) mà chúng tôi đã đề cập ở bài viết trước.
Dựa vào công thức ở trên vì giá trị e và π là các giá trị không thay đổi vì vậy phân phối xác suất của X sẽ phụ thuộc vào trung bình và độ lệch chuẩn, khi 2 giá trị này khác nhau thì phân phối xác suất của X sẽ khác đi. Nếu chúng ta tính xác suất của một biến ngẫu nhiên X nhận giá trị trong một khoảng nào đó trên trục số thì chúng ta phải lập bảng tính xác suất cho từng giá trị (đặc biệt đây là biến liên tục chứa giá trị là số thập phân, không phải biến rời rạc có thể đếm được), và việc tính toán nặng nề và phức tạp.
Lúc này các chuyên gia thống kê sẽ đưa phân phối chuẩn tổng quát về phân phối chuẩn tắc đơn giản (Standard normal distribution) và lập một bảng số tính toán xác suất cho các biến ngẫu nhiên được chuẩn hóa bằng công thức Z-score, và bảng này gọi là bảng tích phân Laplace. Chuẩn hóa các giá trị của biến X bằng công thức Z-score:
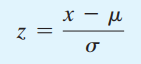
Hàm mật độ xác suất sẽ đơn giản thành:
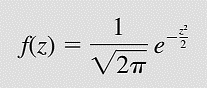
Xác suất của X sẽ được tính bằng xác suất của Z với công thức tích phân Laplace:
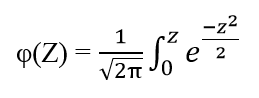
Thông thường khi có giá trị Z được chuẩn hóa từ x, chúng ta sẽ tra bảng tích phân Laplace để tìm ra xác suất nhanh hơn. Đồ thị của phân phối chuẩn tắc cũng giống đồ thị của phân phối chuẩn nhưng giá trị µ =0, σ2 = 1
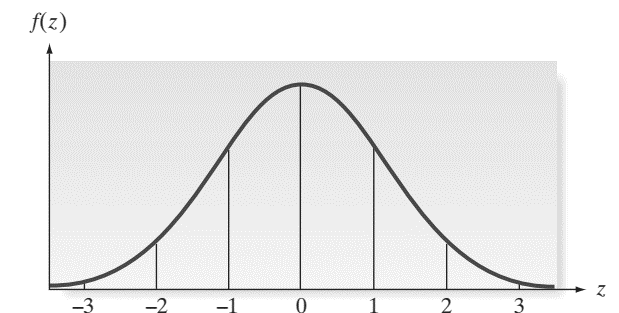
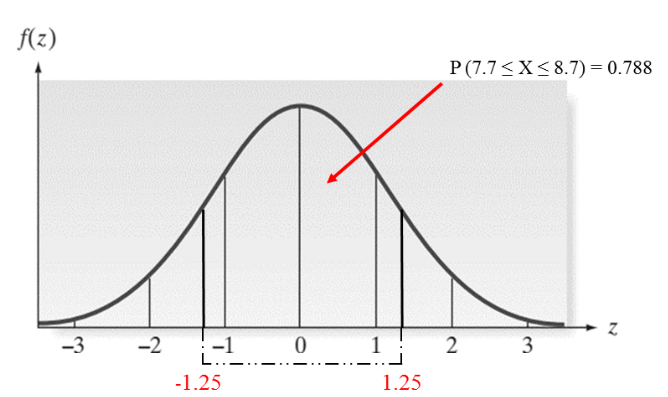
Ví dụ trọng lượng của một sản phẩm A có phân phối chuẩn với µ = 8.2 kg, σ = 0.4, tìm xác suất để lấy được 1 sản phẩm trọng lượng từ 7.7 kg đến 8.7 kg.
P (7.7 ≤ X ≤ 8.7) = P (((7.7 – 8.2)/0.4) ≤ Z ≤ ((8.7 – 8.2)/0.4)) = P (-1.25 ≤ Z ≤ 1.25) = P (-1.25 ≤ Z ≤ 0) + P (0 ≤ Z ≤ 1.25) = φ (1.25) – φ (-1.25) = φ (1.25) + φ (1.25)
Tra bảng tích phân laplace: φ (1.25) = 0.394 vậy P (7.7 ≤ X ≤ 8.7) = 0.788
Phần diện trích giới hạn bởi đường cong hàm mật độ và 2 giá trị từ -1.25 đến 1.25 chính là xác suất của P (7.7 ≤ X ≤ 8.7) = 0.788
Phân phối mẫu (Sampling Distribution) – phân phối trung bình mẫu
Từ tổng thể, chúng ta có thể chọn được nhiều mẫu khác nhau. Nếu mỗi mẫu được lấy ngẫu nhiên thì các tham số mẫu như trung bình của mẫu, tỷ lệ mẫu, và phương sai mẫu là những đại lượng ngẫu nhiên tuân theo những quy luật phân phối nhất định. Vì các tham số mẫu được dùng để xác định các tham số của tổng thể, như trung bình tổng thể, tỷ lệ tổng tể, phương sai của tổng thể, còn gọi là phương pháp ước lượng (ước lượng điểm và khoảng mà chúng tôi sẽ giới thiệu ở phần sau). Do đó chúng ta cần quan tâm đến sự phân phối của các tham số mẫu. Lưu ý trong bài viết này chúng tôi chỉ đề cập đến phân phối của trung bình mẫu., còn phương sai mẫu và tỷ lệ mẫu các bạn có thể tham khảo thêm tài liệu bên ngoài.
Để tìm ra quy luật phân phối mẫu không phải đơn giản, nên các chuyên gia thống kê thường hướng đến giải định tổng thể có phân phối chuẩn, là phân phối phổ biến đối với các hiện tượng kinh tế, xã hội. Do đó những quy luật phân phối mẫu từ giả định này cũng thông dụng, và dễ dàng tính toán.
Định lý giới hạn trung tâm (Central Limit Theorem)
Khi tổng thể mà từ đó chúng ta chọn mẫu không có phân phối chuẩn, thì định lý giới hạn trung tâm sẽ hữu ích trong việc xác định quy luật phân phối của trung bình mẫu. Định lý giới hạn trung tâm trong thống kê suy luận phát biểu như sau: “Nếu chúng ta chọn một mẫu ngẫu có kích thước n đơn vị từ tổng thể có trung bình là µ và độ lệch chuẩn là σ, vậy khi kích thước mẫu được chọn ngày càng lớn thì phân phối của trung bình mẫu sẽ có thể xấp xỉ, hay tiến gần phân phối chuẩn.” Các tham số của mẫu và tổng thể như sau:

Xét trường hợp tổng thể của đại lượng ngẫu nhiên X có phân phối chuẩn (Normal probability distribution), thì trung bình mẫu chắc chắn sẽ có phân phối chuẩn bất kể kích thước mẫu là bao nhiêu. Trong hầu hết các trường hợp, phân phối của trung bình mẫu có thể được xấp xỉ phân phối chuẩn bất cứ khi nào mẫu có kích thước từ 30 trở lên. (n ≥ 30) mà không cần quan tâm đến quy luật phân phối của tổng thể.

Ví dụ theo thống kê tháng trước, năng suất trung bình của 1 công nhân trong một nhà máy sản xuất là 36 kg/ngày, độ lệch chuẩn là 4 kg/ngày. Trong đợt kiểm tra vào giữa tháng này, công ty chọn ra mẫu ngẫu nhiên 30 công nhân hãy tính xác suất để năng suất trung bình mỗi công nhân trong mẫu này sẽ lớn hơn 37.5 kg/ngày? Theo định lý giới hạn trung tâm, phân phối của trung bình năng suất một công nhân trong mẫu lấy ra có thể xấp xỉ phân phối chuẩn với µ = 36 kg/ngày, và độ lệch chuẩn (4/căn bậc 2 của 30) bằng 0.73 kg/ngày.
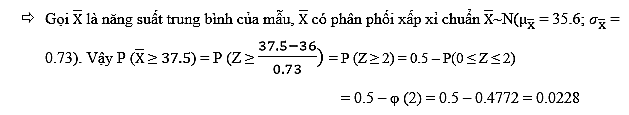
Do Z có giá trị dương nên phần diện tích thể hiện xác suất cần tìm sẽ nằm ở phần bên phải có tổng diện tích bằng 0.5 (đồ thị hình chuông của hàm mật độ xác suất của phân phối chuẩn được chia làm hai mỗi bên là 0.5), vậy chúng ta chỉ cần tìm phần xác suất từ giá trị 0 đến giá trị Z = 2 bị giới hạn mới đường cong hàm mật độ, rồi lấy 0.5 trừ ra. Quay trở lại với định lý giới hạn trung tâm: Z chính là hệ số chuẩn hóa của giá trị x có công thức ((µ – x)/σ) vậy khi hệ số Z sẽ tiến gần đến giá trị 0 thì giá trị x tiến gần đến hoặc gần bằng trung bình µ của tổng thể.
Xét cho trường hợp trung bình của mẫu có phân phối là xấp xỉ chuẩn với trung bình là µ và độ lệch chuẩn là σ/ vậy nếu chúng ta tăng cỡ mẫu thì độ lệch chuẩn này sẽ giảm dần, đồ thị hình chuông hẹp vô, và nhọn hơn, các giá trị trung bình mẫu sẽ ổn định xung quanh trung bình µ của tổng thể.
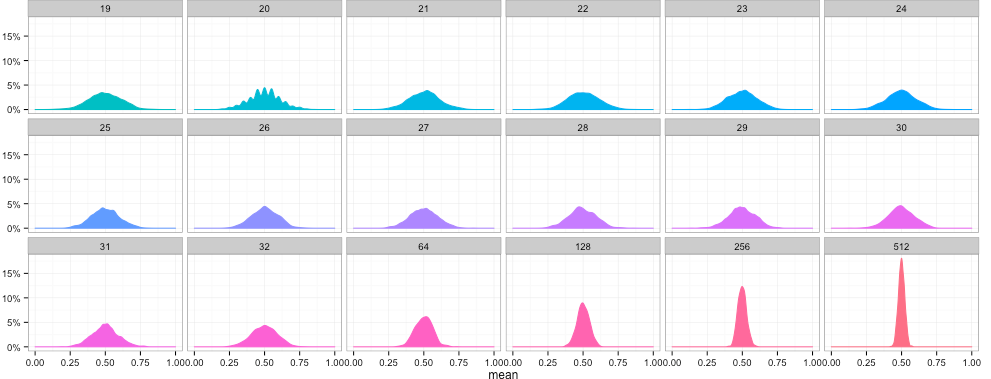
Hình: minh họa định lý giới hạn trung tâm (nguồn En.wikipedia)
Lưu ý nữa là khi cỡ mẫu tăng đồ thị có xu hướng cao lên, giải thích là phạm vi các giá trị trung bình mẫu có thể bị thu hẹp do chúng đã ổn định xung quanh giá trị trung bình của tổng thể, lúc này xác suất xảy ra của mỗi giá trị trung bình mẫu sẽ tăng lên.
Tóm lại sau cùng, từ một tổng thể có trung bình là µ, nếu chúng ta lấy mẫu có kích thước ngày càng lớn, thì khả năng trung bình mẫu lấy được gần bằng trung bình tổng thể là rất cao. Đây cũng là lí do tại sao chúng ta cần nhiều dữ liệu hơn nếu có thể.
Ước lượng (Estimation)
Phần ước lượng và phần kiểm định giả thuyết ở phía sau bài viết chính là phần kiến thức trọng tâm thể hiện rõ nhất bản chất của Inferential Statistics (thống kê suy luận). Nhưng chắc chắn sẽ có bạn thắc mắc tại sao đến đây BigDataUni mới trình bày? Chúng ta cùng đi quy trình ngược trở lại nhé: ước lượng và kiểm định giúp đưa ra các suy luận về tổng thể dựa trên các tham số mẫu, vậy để hiểu được tham số mẫu đặc biệt là trung bình mẫu thì chúng ta phải đi qua phân phối trung bình mẫu trong đó có phân phối chuẩn, để hiểu được phân phổi chuẩn chúng ta phải đi qua các quy luật phân phối thông dụng.
Trở lại với ước lượng thì có 2 loại ước lượng đó là ước lượng điểm (Point Estimation) và ước lượng khoảng (Interval Estimation)
Ước lượng là gì? Giải thích “cực kỳ” đơn giản để các bạn hiểu: giả sử chúng ta không biết gì về tổng thể, chúng ta chỉ có một dữ liệu mẫu và tính toán được các tham số mẫu như trung bình mẫu , độ lệch chuẩn mẫu s, tỷ lệ mẫu vậy từ các tham số mẫu này chúng ta có suy luận ra được các tham số tổng thể như trung bình µ, độ lệch chuẩn tổng thể σ, tỷ lệ tổng thể p, chính vì vậy chúng ta gọi đây là thống kê suy luận
Ước lượng điểm (Point Estimation)
Ước lượng điểm nghĩa là chúng ta dùng các tham số mẫu ước lượng trực tiếp các tham số tổng thể, không xem xét đến mức độ chênh lệch thực tế. Ví dụ một trường đại học nhận được hơn 800 đơn đăng ký nhập học từ các sinh viên trong 3 ngày. Mẫu đơn đăng ký chứa nhiều thông tin khác nhau, ví dụ điểm thi đại học và thông tin sinh viên có mong muốn ở ký túc xá hay không.
Trong một cuộc họp sắp diễn ra ở vài tiếng sắp tới, ban quản lý nhà trường muốn thông báo về điểm đại học trung bình đầu vào của 800 sinh viên xin nhập học và tỷ lệ sinh viên muốn ở tại ký túc xá Tuy nhiên thông tin của 800 sinh viên này vẫn chưa được nhập liệu đầy đủ. Do đó ban quản lý nhà trường phải lấy ra ngẫu nhiên 30 sinh viên từ hệ thống máy tính. Từ đây họ tính được các tham số mẫu, dùng để ước lượng cho tổng thể 800 sinh viên, và đem thông tin này trình bày trong cuộc họp, giả sử có được kết quả sau:
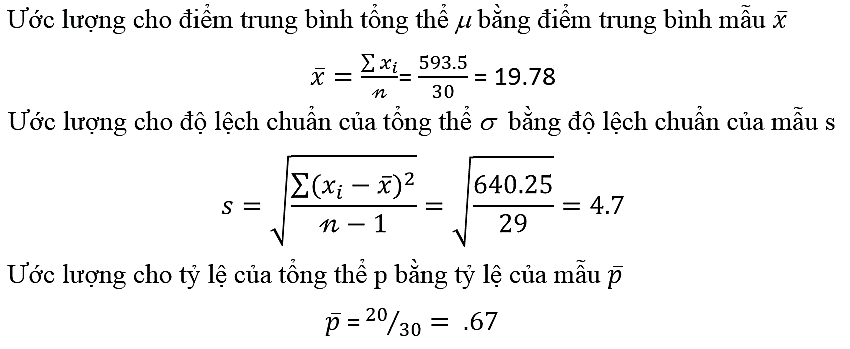
Lưu ý là nếu các mẫu được chọn khác nhau, có đơn vị mẫu khác nhau mặc dù kích thước mẫu có giữ nguyên thì các tham số mẫu có thể thay đổi dẫn đến giá trị ước lượng có thể thay đổi. Kết thúc tuần tuyển sinh, quá trình nhập liệu đã được tính đầy đủ lúc này trường đại học có thể tính các tham số tổng thể từ đó biết được, trung bình điểm đại học đầu vào của 800 sinh viên ví dụ là 22,3 điểm, độ lệch chuẩn ví dụ là 5.3 điểm, tỷ lệ sinh viên đăng ký ở tại ký túc xá ví dụ là 0.63. Chúng ta dùng các con số để ước lượng cho các hằng số chưa biết của tổng thể nên việc đưa ra con số chính xác là điều không thể, thay vào đó sử dụng ước lượng khoảng.
Ước lượng khoảng (Interval Estimation)
Chúng ta có thể ước lượng chính xác hơn giá trị của các tham số tổng thể nếu xây dựng một khoảng số gọi là khoảng ước lượng, và khoảng này có khả năng cao chứa các tham số của tổng thể. Khoảng ước lượng cho trung bình tổng thể có công thức tổng quát như sau:

Minh họa bằng độ thị phân phối chuẩn tắt của Z:
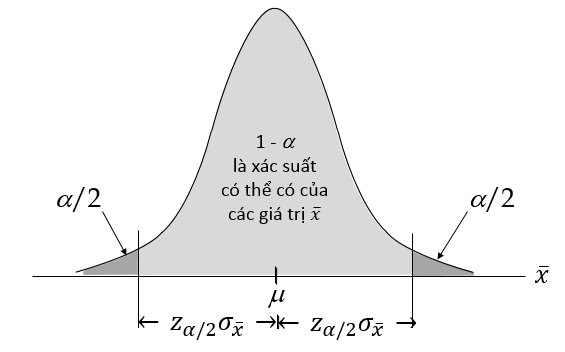
Dựa trên độ tin cậy gọi là Confidence level tức là xác suất ứng với khả năng trung bình tổng thể µ nằm trong khoảng ước lượng tính được. Ở bài toán phân phối mẫu cho trung bình mẫu mà chúng ta vừa làm ở phần 3, chúng ta sẽ sử dụng phân phối xấp xỉ chuẩn để tìm ra xác suất của một giá trị trung bình mẫu (cho trước) có thể xảy ra. Ở bài toán ước lượng chúng ta làm ngược lại là dựa vào xác suất đã cho để tìm ra khoảng ước lượng có chứa trung bình tổng thể tức tìm ra sai số là chênh lệch của trung bình mẫu và trung bình tổng thể.
Nói có vẻ khó hiểu, để BigDataUni đi vào ví dụ sẽ dễ dàng hơn để các bạn nắm bắt. Lưu ý độ tinh cậy = 1 – alpha Công thức tổng quát về ước lượng khoảng mà chúng tôi đề cập ở trên dành cho trường hợp mẫu ngẫu nhiên n ≥ 30 và độ lệch chuẩn của tổng thể đã biết, và tổng thể có phân phối chuẩn, trung bình mẫu cũng sẽ có phân phối chuẩn, chúng ta có thể sử dụng bảng phân phối chuẩn tích lũy để tra giá trị Z.
Trường hợp khác nếu tổng thể có phân phối chuẩn mà phương sai của tổng thể chưa biết, chúng ta có thể thay độ lệch chuẩn của mẫu vào công thức để tính. Trường hợp khác nếu tổng thể có phân phối chuẩn, độ lệch chuẩn chưa biết mà mẫu lấy ra nhỏ hơn 30 thì phân phối trung bình mẫu lúc này không sử dụng quy luật phân phối chuẩn tắc Z mà sử dụng phân phối t (t/Student distribution) và độ lệch chuẩn của mẫu s để tính khoảng ước lượng. Công thức ước lượng như sau:
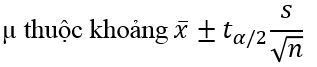
Giá trị t tìm được bằng cách tra bảng phân phối t với α/2 và bậc tự do là n – 1. Minh họa cho phân phối t Student:
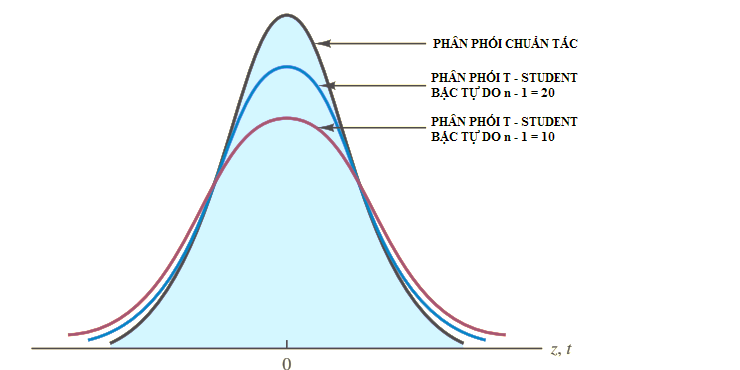
Ví dụ minh họa:
- Một máy đóng nước tự động vào chai được điều chỉnh để lượng nước đóng vào chai có phân phối chuẩn và độ lệch chuẩn là 0.05 lít, với khoảng tin cậy là 95%, lấy mẫu 40 chai thì thấy lượng nước trung bình mỗi chai là 0.65 lít, hãy ước lượng lượng nước trung bình mỗi một chai xét trên tất cả các chai được đóng bởi máy này.
Với độ tin cậy là 95% thì chúng ta có α = 0.05, vậy Z α/2 = Z0.025 tức chúng ta kiếm giá trị 1 – 0.025 = 0.975 (trên bảng phân phổi chuẩn tích lũy) rồi tham chiếu qua cột ngoài cùng thấy giá trị là 1.9, tham chiếu trên dòng trên cùng là 0.06, vậy Z0.025 = 1.96. Thay vào công thức: 0.65 ± 1.96* (0.05/(căn bậc 2 của 40)) = 0.65 ± 0.016. Vậy lượng nước trung bình tổng thể nằm trong khoảng từ 0.634 lít đến 0.666 lít.
- Một mẫu gồm 10 hộp kem dưỡng da hiệu A có khối lượng trung bình là 40.5 g, độ lệch chuẩn 0.8 g. Với khoảng tin cậy 90% ước lượng khối lượng trung bình của tất cả hộp kem hiệu A, biết khối lượng của hộp kem có phân phối chuẩn.
Với độ tin cậy là 90%, α = 0.1, n = 10, bậc tự do sẽ là 9, chúng ta tra bảng phân phối t Student với α/2 = 0.05. Vậy t9, 0.05 = 1.833 Thay vào công thức: 40.5 ± 1.833*(0.8/(căn bậc 2 của 10)) = 40.5 ± 0.46. Vậy khối lượng trung bình µ nằm trong khoảng (40.04 g; 40.96 g Ngoài ra còn có công thức ước lượng cho tỷ lệ tổng thể p:
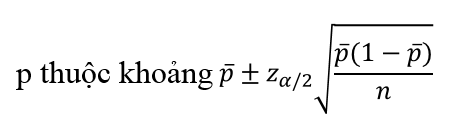
Ví dụ lấy mẫu ngẫu nhiên 100 người khảo sát thì có 60 người cho rằng họ ưa chuộng dịch vụ giao hàng tận nơi, thì với độ tin cậy là 95% thì tỷ lệ này là bao nhiêu nếu xét cả thành phố, tìm ra khoảng ước lượng? Cách thức cũng làm đơn giản, các bạn hãy thử tìm ra kết quả nhé!
Kiểm định giả thuyết (Hypothesis test)
Ngoài việc chúng ta sử dụng các tham số mẫu để ước lượng các đặc trưng của tổng thể chúng ta có còn có thể đánh giá một giả thuyết nào đó về các tham số của tổng thể, quy luật phân phối của tổng thể là đúng hoặc sai. Lý thuyết về kiểm định giả thuyết là rất nhiều, và phức tạp hơn nhiều so với phần ước lượng nên trong bài viết này chúng tôi chỉ giới thiệu tổng quan về lý thuyết kiểm định giả thuyết và không trình bày cụ thể từng ví dụ, mong các bạn thông cảm.
Một tổng thể có các đặc trưng chưa biết như trung bình tổng thể, phương sai của tổng thể, tỷ lệ của tổng thể, các đặc trưng này ký hiệu là θ, θo là cái cần kiểm chứng Chúng ta sẽ đặt giả thuyết H0 và giả thuyết H1 là giả thuyết đối của H0 Nếu kiểm định 2 bên (Two – tail test)
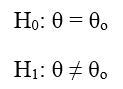
Nếu kiểm định 1 bên (One – tail test)
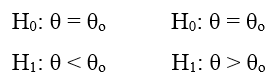
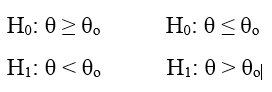
Các sai lầm thường mắc khi kiểm định giả thuyết:
- Giả thuyết H0 đúng (tức thực tế θ = θo) nhưng qua kiểm định chúng ta kết luận sai, nghĩa là θ ≠ θo vậy ta bác bỏ H0. Đây là sai lầm loại I tức chúng ta bác bỏ giả thuyết H0 khi giả thuyết này đúng.
- Giả thuyết H0 sai nhưng qua kiểm định chúng ta kết luận đúng, và không bác bỏ. Đây là sai lầm loại II, tức chúng ta không bác bỏ H0 khi giả thuyết này sai.
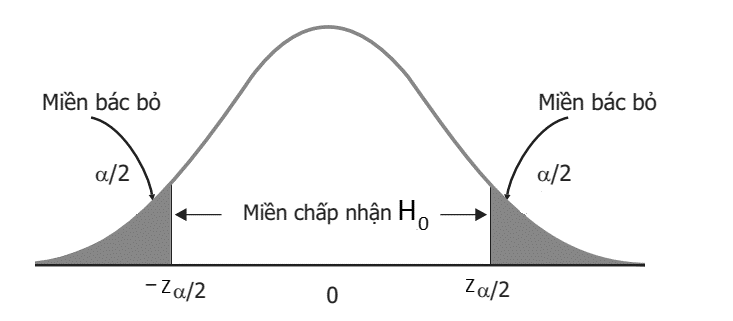
Hình minh họa đồ thị phân phối chuẩn kiểm định giả thuyết 2 bên
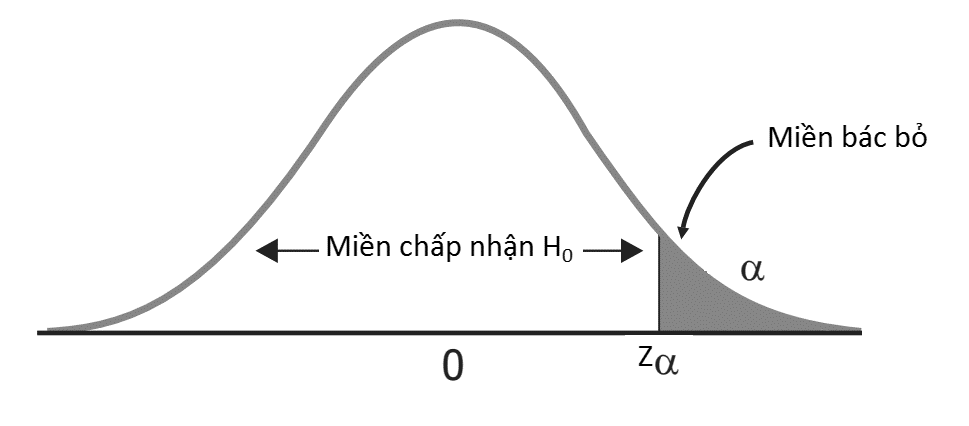
Hình minh họa đồ thị phân phối chuẩn kiểm định giả thuyết 1 bên (H1 = θ > θo)
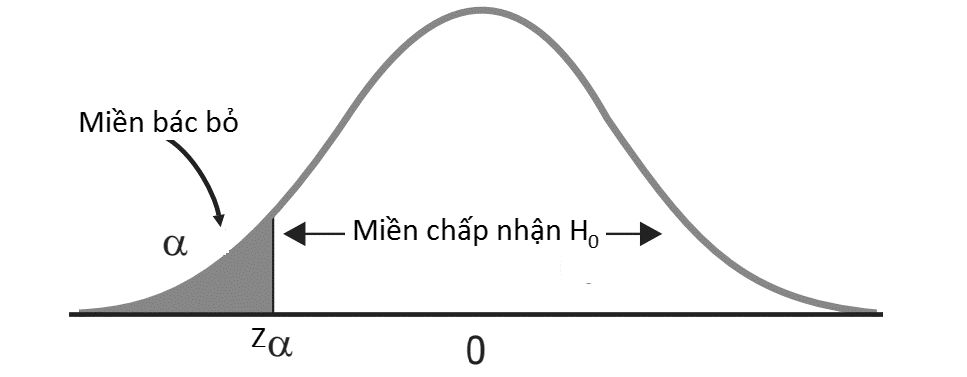
Hình minh họa đồ thị phân phối chuẩn kiểm định giả thuyết 1 bên (H1 = θ < θo)Công thức tính giá trị kiểm định:Kiểm định trung bình tổng thể:
- n ≥ 30
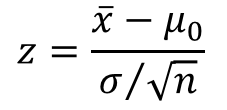
- n < 30
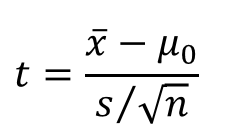
Quy tắc bác bỏ, tra bảng Zα và Zα/2
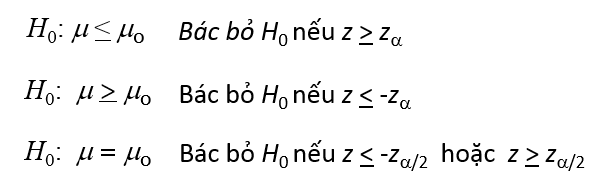
Quy tắc bác bỏ, tra bảng t Student bậc tự do n – 1
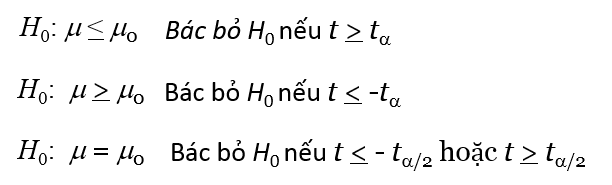
Kiểm định tỷ lệ tổng thể: Điều kiện áp dụng: n.p ≥ 5 và n.(1 – p) ≥ 5
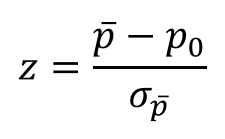
Với
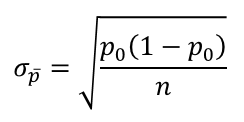
Quy tắc bác bỏ, Zα và Zα/2 tra bảng
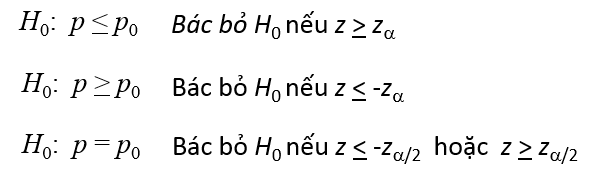
Giá trị p-value: Là mức ý nghĩa nhỏ nhất mà ở đó giả thuyết H0 bị bác bỏ, tìm giá trị p-value bằng cách tra bảng Z, và tra bảng t Student với các giá trị kiểm định tính toán được. Ví dụ Z = – 1.79 chúng ta có φ(-1.79) = 0.4633 (giá trị này tra bảng phân phối chuẩn không tích lũy tức P(0<Z<1.79)). Nếu kiểm định 2 bên thì p-value/2 = 0.5 – 0.4633 = 0.0367 vậy p-value = 7.34%. Nếu quy định trước một mức ý nghĩa α nào đó thì:
- p-value ≤ α thì bác bỏ giả thuyết H0, chấp nhận H1
- p-value > α thì chưa có cơ sở bác bỏ H0
Ngoài ra còn rất nhiều công thức khác về kiểm định và ước lượng trong thống kê suy luận mà chúng tôi không thể trình bày hết ở đây, các bạn có thể tham khảo thêm ở các tài liệu khác, mục đích chính của bài viết lần này BigDataUni muốn giới thiệu đến các bạn những kiến thức nào trong thống kê suy luận mà các bạn cần phải nắm mà thôi, còn chi tiết như thế nào thì một bài viết không thể thể hiện hết tất cả
Đến đây là kết thúc bài viết về thống kê suy luận cũng như kết thúc chủ đề bài viết về thống kê. Trong quá trình tham khảo nếu thấy có gì sai sót mong các bạn góp ý, và tiếp tục ủng hộ BigDataUni ở các bài viết sắp tới.
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English