Thuật toán KNN và ví dụ đơn giản

Giới thiệu về K – nearest neighbor (KNN)

Ở các bài viết trước BigDataUni đã giới thiệu đến các bạn một cách tổng quan những chủ đề về Data mining (Khai phá dữ liệu), Predictive analytics (Phân tích dự báo), Statistics (Thống kê) bao gồm các khái niệm quan trọng, kỹ thuật phân tích và ứng dụng, lợi ích trong các lĩnh vực khác nhau.

Trong những bài viết sắp tới, chúng tôi sẽ hướng đến cách tiếp cận phân tích dữ liệu, cụ thể là các case study sử dụng những phương pháp trong Data mining, Predictive analytics hay Statistics phục vụ cho các hoạt động kinh doanh của các công ty thuộc ngành tài chính ngân hàng (Banking), cho đến bán lẻ, thương mại điện tử (Online retail/ E-commerce).

Lưu ý, chúng tôi sẽ chỉ trình bày cơ bản lý thuyết về mỗi phương pháp phân tích, và ví dụ về ứng dụng phổ biến của nó ở từng lĩnh vực. Cách thức thực hiện phân tích, hay nói cách khác là sử dụng công cụ phân tích gì, từng bước triển khai trên công cụ đó ra sao chúng tôi sẽ không đề cập. Ví dụ ở bài viết hôm nay về thuật toán K-nearest neighbor (KNN – K láng giềng gần nhất), thông thường nếu các bạn search trên Google sẽ thấy rất nhiều bài viết nói về KNN và cách sử dụng Python hay R để phân tích KNN. Tuy nhiên chúng tôi không làm như vậy, chúng tôi cho rằng hướng tiếp cận, nắm được mục đích của phương pháp phân tích, hiểu được nó, biết nó dùng trong trường hợp nào mới là quan trọng nhất.

Quay trở lại với Data mining, thì một trong những kỹ thuật phân tích cốt lõi, phổ biến nhất đó chính là Classification – thuật toán phân loại. Nếu bạn nào chưa biết về các phương pháp trong Data mining thì có thể tham khảo qua bài viết sau:

TỔNG QUAN VỀ DATA MINING (P3): QUÁ TRÌNH VÀ PHƯƠNG PHÁP

Trong thống kê, đặc biệt là thống kê suy luận chúng ta có phương pháp ước lượng (Estimation) bao gồm ước lượng điểm (Point estimation) và ước lượng khoảng (Interval estimation) dựa trên các tham số của mẫu để suy ra các tham số của tổng thể. Thuật toán Classification – phân loại, cũng gần giống với Estimation, tuy nhiên thay vì kết quả của quá trình ước lượng là dữ liệu định lượng (hay biến định lượng, Quantitative variables) thì đầu ra sau cùng của thuật toán phân loại là dữ liệu đính tính (hay biến định tính, Qualitative/ Categorical variables).

Ví dụ kết quả đầu ra của Classification có thể là đánh giá mức thu nhập của khách hàng tiềm năng của một ngân hàng có thể là High income (thu nhập cao), Middle income (thu nhập trung bình) và Low income (thu nhập thấp). Giả sử nhân viên ngân hàng muốn phân loại khách hàng mới (chưa được phân loại) vào các nhóm thu nhập kể trên thì phải làm sao? Họ sẽ phân tích các yếu tố kết hợp khác nhau như độ tuổi, giới tính, nghề nghiệp để xem xét, với cơ sở là đã có sẵn một tập dữ liệu với những khách hàng cũ trước đây đã được phân loại dựa trên chính các yếu tố đó. Qua đó các thuật toán sẽ xác định một nhóm bao gồm những biến nào có liên hệ với biến mục tiêu (target) ví dụ khách hàng là nam, độ tuổi trung niên, nghề ngiệp là giám đốc quản lý thì có thể có thu nhập cao tức High income. Tập dữ liệu sử dụng ở đây gọi là “Training data set”, phục vụ cho việc xây dựng mô hình phân loại. Tiếp theo, sau khi đã tìm ra cách thức phân loại phù hợp trên Training data set, các thuật toán sẽ tiến hành phân loại cho dữ liệu mới ví dụ phân loại thu nhập cho khách hàng mới (giả định ngân hàng chưa thông tin về thu nhập): khách hàng mới là nam, độ tuổi trung niên, nghề nghiệp là doanh nhân có khả năng có thu nhập cao.

Bên trên là minh họa đơn giản cho phương pháp Classification trong Data mining. Có nhiều thuật toán phân loại khác nhau trong khai phá dữ liệu phổ biến như K-Nearest Neighbor (KNN), Decision Trees (Cây quyết định), Neural network, Naïve Bayes, v.v.

Ở bài viết lần này chúng tôi sẽ giới thiệu đến các bạn lý thuyết cơ bản về thuật toán phân loại đầu tiên chính K láng giềng gần nhất hay còn gọi K-nearest neighbor với ứng dụng của nó trong ngành ngân hàng để phân loại khách hàng có khả năng mang lại rủi ro tín dụng cao.

Lưu ý: các phương pháp đánh giá tính hiệu quả của mô hình thuật toán Classification như error rate, Confusion Matrix, Recall, Precision, ROC, AUC, v.v chúng tôi sẽ trình bày tổng thể trong bài viết khác để các bạn tham khảo rõ hơn. Còn trong bài viết này, chúng tôi chỉ dừng lại ở kết quả của thuật toán K-NN mà thôi.

K – nearest neighbor (KNN)

Thuật toán KNN là một trong những phương pháp học có giám sát “Supervised Learning” tức dựa trên biến mục tiêu đã được xác định trước đó, thuật toán sẽ xem xét dữ liệu đã chứa biến mục tiêu (đã phân loại) để “học” và tìm ra những biến d có thể tác động đến biến mục tiêu.

KNN dựa trên giả định là những thứ tương tự hay có tính chất gần giống nhau sẽ nằm ở vị trí gần nhau, với giả định như vậy, KNN được xây dựng trên các công thức toán học phục vụ để tính khoảng cách giữa 2 điểm dữ liệu (gọi là Data points) để xem xét mức độ giống nhau của chúng.

KNN còn gọi là “Lazy learning method” vì tính đơn giản của nó, có nghĩa là quá trình training không quá phức tạp để hoàn thiênhj mô hình (tất cả các dữ liệu đào tạo có thể được sử dụng để kiểm tra mô hình KNN). Điều này làm cho việc xây dựng mô hình nhanh hơn nhưng giai đoạn thử nghiệm chậm hơn và tốn kém hơn về mặt thời gian và bộ nhớ lưu trữ, đặc biệt khi bộ dữ liệu lớn và phức tạp với nhiều biến khác nhau. Trong trường hợp xấu nhất, KNN cần thêm thời gian để quét tất cả các điểm dữ liệu và việc này sẽ cần nhiều không gian bộ nhớ hơn để lưu trữ dữ liệu. Ngoài ra KNN không cần dựa trên các tham số khác nhau để tiến hành phân loại dữ liệu, không đưa ra bất kỳ kết luận cụ thể nào giữa biến đầu vào và biến mục tiêu, mà chỉ dựa trên khoảng cách giữa data point cần phân loại với data point đã phân loại trước đó. Đây là một đặc điểm cực kỳ hữu ích vì hầu hết dữ liệu trong thế giới thực tại không thực sự tuân theo bất kỳ giả định lý thuyết nào ví dụ như phân phối chuẩn trong thống kê.

Các bước thực hiện thuật toán có thể đơn giản như sau:

Chuẩn bị dữ liệu (dữ liệu đã được làm sạch, chuyển đổi, sẵn sàng đưa vào phân tích), chia tập dữ liệu ra làm 2: training data set (để train model) và test data set (để kiểm chứng model)
Chọn một số K bất kỳ, K là một số nguyên, tức là số điểm dữ liệu đã phân loại có khoảng cách ngần nhất (láng giềng gần nhất) với điểm dữ liệu chưa phân loại
Tính toán khoảng cách giữa điểm dữ liệu chưa phân loại với các điểm dữ liệu đã được phân loại.
Với kết quả có được sắp xếp theo thứ tự với giá trị khoảng cách từ bé nhất đến lớn nhất
Chọn ra các điểm dữ liệu có giá trị khoảng cách bé nhất với điểm dữ liệu cần phân loại dựa trên K cho trước, ví dụ nếu K = 2 tức chọn ra 2 điểm dữ liệu gần nhất, K = 3 là 3 điểm dữ liệu gần nhất.
Tiếp theo xem xét giá trị của biến mục tiêu (biến phân loại) của các điểm dữ liệu gần nhất, chọn ra giá trị xuất hiện nhiều nhất và gán cho điểm dữ liệu chưa phân loại, ví dụ K = 3, trong đó có 2 điểm dữ liệu được phân loại là A, điểm còn lại là B thì điểm dữ liệu chưa phân loại lúc này sẽ được phân loại là A.
Kiểm chứng lại độ hiệu quả của model trên test data set, và sử dụng các phương pháp đánh giá khác nhau. (các phương pháp đánh giá mô hình phân loại sẽ được chúng tôi trình bày tổng quan trong bài viết sau)
Thay đổi giá trị K khác nhau và thực hiện lại quy trình để tìm được K tối ưu nhất cho tập dữ liệu

Bước khó khăn nhất của thuật toán KNN, và cũng là bước đau đầu nhất, cần sự kinh nghiệm của nhà phân tích, đó chính là chọn K là bao nhiêu. Nhưng trước hết chúng ta cùng đi qua ví dụ cụ thể sau đây để biết được cách tính khoảng cách giữa các điểm dữ liệu.

Ví dụ sau được tham khảo từ giáo trình Data mining nổi tiếng: “Discovering Knowledge in Data: An introduction to Data mining” của Daniel T.Larose (phần 2)

Giả sử một bệnh viện tiến hành phân loại thuốc chỉ định cho những bệnh nhân mới dựa trên độ tuổi (Age) và tỷ lệ Na/K trong máu.

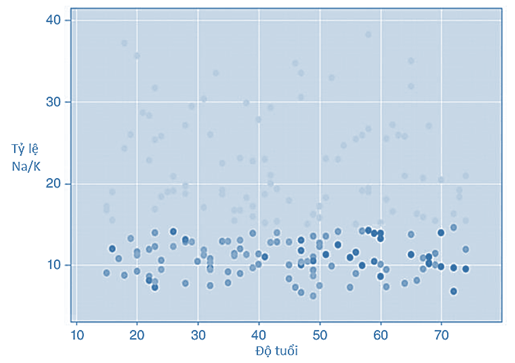
Bên trên là độ thị Scatter Plot, trục hoành là độ tuổi, trục tung là tỷ lệ Na/K, mỗi điểm trên đồ thị là một bệnh nhân tương ứng với tỷ lệ Na/K, và độ tuổi cho trước. Màu sắc khác nhau thể hiện cho loại thuốc chỉ định. Màu xanh nhạt là loại thuốc M, màu xanh trung bình là loại thuốc N, màu xanh đậm là loại thuốc P.

Giả sử bệnh viện tiếp nhận các bệnh nhân mới (ví dụ bệnh nhân A và B) và cần tiến hành phân loại thuốc cho họ. Đồ thị tiếp theo dưới đây chứa các bệnh nhân mới chưa được phân loại, dựa vào độ tuổi, và tỷ lệ Na/K chúng ta xác định được những vùng trên đồ thị sẽ là nơi chứa các data point của các bệnh nhân mới này. Nhiệm vụ là xác định loại thuốc thích hợp cho bệnh nhân A, B trên cơ sở là xác định khoảng cách giữa điểm dữ liệu của A, và B (chưa được phân loại thuốc) và điểm dữ liệu đã phân loại (bệnh nhân cũ trước đây đã được phân loại thuốc), khoảng cách gần nhất thì khả năng loại thuốc được phân loại sẽ tương đương nhau giữa 2 bệnh nhân.

Trước tiên chúng ta xét bệnh nhân A giả sử có độ tuổi là 40 và tỷ lệ Na/K gần 29, thì thấy rằng điểm dữ liệu của bệnh nhân này nằm trong vùng chứa có các điểm dữ liệu màu xanh nhạt tức nằm chung vùng với các bệnh nhân trước đây được phân loại thuốc là M. Do đó bệnh nhân mới số 1 sẽ được phân loại thuốc là M. Ở đây chúng ta không cần đặt giá trị K để tìm ra các điểm gần nhất do xung quanh của điểm dữ liệu bệnh nhân A toàn là các điểm màu xanh nhạt. (Hình đồ thị dưới đây được điều chỉnh màu sắc để các bạn nhìn rõ các điểm)

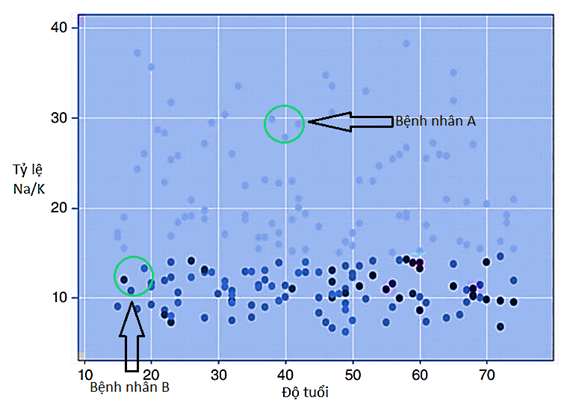
Xét tiếp bệnh nhân B, lưu ý hình đã được chúng tôi cân chỉnh lại màu sắc để hiển thị rõ màu sắc khác nhau giữa các điểm giúp các bạn dễ phân biệt. Giả sử zoom lại gần vùng chứa điểm dữ liệu của bệnh nhân B chúng ta có hình dưới đây.

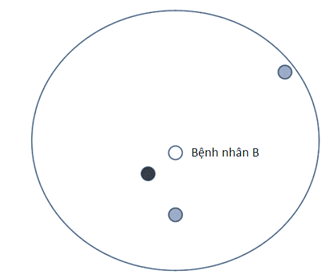
Nếu chúng ta lấy K = 1 tức chỉ xét 1 điểm gần nhất so với điểm dữ liệu của bệnh nhân B, thì điểm dữ liệu bệnh nhân B gần nhất với điểm màu xanh đậm nhất, ứng với bệnh nhân B sẽ được phân loại thuốc là P. Nếu chúng ta lấy K = 2 tức xét 2 điểm gần nhất, thì điểm dữ liệu B sẽ gần với 1 điểm xanh đậm và 1 điểm màu xanh trung bình, tức là bệnh nhân B có thể được phân loại thuốc là P hoặc là N. Do đó chúng ta chưa tìm ra đâu là loại thuốc thích hợp nhất cho B, vậy K = 2 không phải là giá trị K cần xét. Tiếp đến chúng ta lấy K = 3, thì trên đồ thị chúng ta thấy có 2 điểm màu xạnh trung bình nhiều hơn so với 1 điểm màu xanh đậm là gần nhất với điểm dữ liệu bệnh nhân B. Vậy với K = 3, bệnh nhân B sẽ được phân loại thuốc là N khi điểm dữ liệu bệnh nhân B gần với nhiều điểm dữ liệu màu xanh trung bình hơn.

Phương pháp trên gọi là Voting, tức tìm ra những điểm dữ liệu phổ biến xuất hiện gần nhất với điểm dữ liệu cần phân loại (trong thống kê cũng có thể gọi là tính Mode). Trở lại ví dụ trên thì với K = 3, số vote cho điểm dữ liệu màu xanh trung bình là 2, còn điểm dữ liệu màu xanh đậm là 1, vậy 2>1, nên bệnh nhân B sẽ được phân loại thuốc là P, độ tin cậy Confidence = 2/3 = 66.7%

Lưu ý quan trọng, chúng ta thường tìm K trước rồi mới khoanh vùng cho điểm dữ liệu chưa phân loại dựa trên việc tính toán các khoảng cách giữa nó so với các điểm dữ liệu đã phân loại. Chúng tôi khoanh vùng trước để dễ dàng trình bày ví dụ đến cho các bạn mà thôi.

Vậy thì việc tính khoảng cách giữa các điểm dữ liệu dựa trên phương pháp nào, thì có 2 phương pháp chính:

Euclidean:

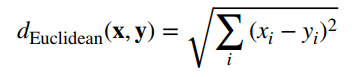
Manhattan:

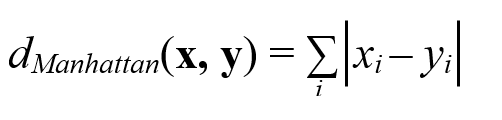
Trong bài viết này chúng tôi sẽ chỉ dùng công thức Euclidean phổ biến nhất để tính toán các khoảng cách giữa các điểm dữ liệu.

Ví dụ bệnh nhân mới D có tuổi là 20, và tỷ lệ Na/K là 12, bệnh nhân cũ E có tuổi là 30, tỷ lệ Na/K là 8. Vậy khoảng cách d_euclidean = căn bậc 2 của (28 – 35)² + (11 – 9)² = 7.28

Trong quá trình tính toán khoảng cách sẽ có những biến chứa các giá trị lớn ví dụ như tiền và những biến chứa giá trị nhỏ ví dụ như độ tuổi, giá trị các khoảng cách được tính sẽ không còn phù hợp và hiệu quả. Lúc này các chuyên gia phân tích thường phải chuẩn hóa dữ liệu.

Ở bài viết thống kê mô tả chúng tôi đã giới thiệu đến các bạn, công thức chuẩn hóa dữ liệu Z-score, còn đến bài viết này các bạn sẽ được biết thêm chuẩn hóa dữ liệu theo Min – max:

Chuẩn hóa dữ liệu Z-score:

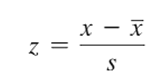
Chuẩn hóa dữ liệu Min – max:

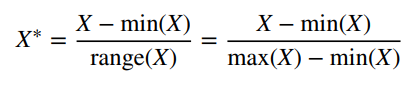
Giá trị chuẩn hóa Z nằm trong khoảng từ -3 đến 3 (theo quy tắc thực nghiệm Empirical Rule trong thống kê) còn giá trị chuẩn hóa Min – Max từ 0 đến 1 do trong độ trải giữa (range) chứa giá trị X. Chuẩn hóa theo Min – Max thường được ưa chuộng hơn khi các biến đầu vào có thêm biến định tính.

Trong trường hợp biến đầu vào phục vụ cho việc phân loại không phải là biến định lượng như độ tuổi hay tỷ lệ Na/K mà là biến định tính ví dụ như tình trạng hôn nhân (độc thân, đã kết hôn), hay giới tính (nam, nữ), chúng ta sẽ dùng quy tắc sau để tính khoảng cách:

X_i– Y_i = 0 nếu có cùng giá trị của biến định tính và bằng 1 nếu ngược lại.

Quay trở lại với cách thức chọn K mà chúng tôi vừa đề cập ở trên là cách thức chọn K đơn giản, hay còn gọi là Simple Unweighted Voting tức mỗi một điểm dữ liệu ở gần điểm dữ liệu cần phân loại sẽ được 1 vote. Ví dụ ở trên khi K = 3 xét cho bệnh nhân B, thì số điểm dữ liệu có màu xanh trung bình là 2, điểm dữ liệu màu xanh đậm là 1 vậy bệnh nhân B được phân loại thuốc theo các điểm màu xanh trung bình, là thuốc P. Tuy nhiên nếu giả sử bệnh nhân C là bệnh nhân mới, cũng với K = 3, nhưng khi tính toán chúng ta lại tìm ra 3 điểm gần với C nhất nhưng mỗi một điểm tương ứng mỗi màu khác nhau, tức màu xanh đậm, xanh trung bình, và xanh nhạt (như hình dưới đây), vậy C được phân loại cho loại thuốc nào, M, N, hay P khi mỗi loại đầu có vote ngang nhau?

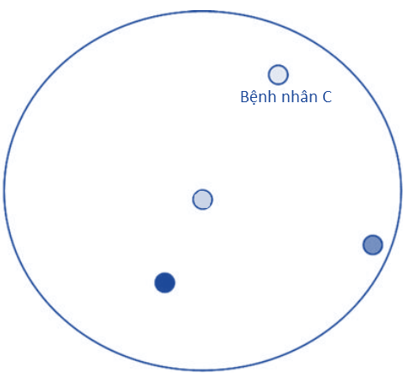
Dưới góc nhìn của các chuyên gia thì những điểm dữ liệu hay data point gần với data point của dữ liệu cần phân loại thì cần có giá trị vote cao hơn, do đó cần sử dụng phương pháp Weighted voting với giá trị vote được tính bằng cách nghịch đảo giá trị bình phương của khoảng cách (trên cơ sở giá trị của dữ liệu đã được chuẩn hóa).

Ngoài ra, trong quá trình xem xét các thuộc tính, hay biến đầu vào, các chuyên gia cho rằng những biến nào có tác động nhiều hơn, có ảnh hưởng nhiều hơn đến biến mục tiêu (biến phân loại) cần được gán trọng số. Dựa trên kinh nghiệm phân tích, cùng với sử dụng các phương pháp trong Data mining, và dưới góc nhìn của mình thì các chuyên gia sẽ có cách thức xác định trọng số khác nhau.

Giả sử ví dụ về phân loại thuốc, các bác sĩ thấy rằng tỷ lệ Na/K quan trọng hơn độ tuổi trong việc phân loại, do đó gán trọng số là 3 và độ tuổi là 1. Tính lại khoảng cách giữa bệnh nhân mới D và bệnh nhân cũ E đã được phân loại thuốc trước đó, chúng ta có:

d_euclidean = căn bậc 2 của (28 – 35)² + 3*(11 – 9)² = 7.8

Như vậy, chúng tôi đã trình bày tổng quan về nhũng kiến thức cơ bản trong việc tính toán khoảng cách giữa 2 điểm dữ liệu, và cách thức tính vote để tìm ra giá trị phân loại chính xác cho đối tượng dữ liệu chưa được phân loại.

Tiếp theo trở lại với vấn đề ban đầu là nên xác định giá trị K sao cho phù hợp, tức là cần bao nhiêu điểm ở gần nhất hay số “láng giềng” gần nhất với điểm dữ liệu cần phân loại?

Đầu tiên, theo lời khuyên của các chuyên gia thì chúng ta nên có phép thử, nghĩa là chạy nhiều mô hình KNN với các giá trị K khác nhau và bắt đầu thử nghiệm từ K = 1, sau đó kiểm tra độ hiệu quả của từng mô hình (dựa trên các phương pháp đánh giá mô hình phân loại mà chúng tôi sẽ giới thiệu ở các bài viết sau), mô hình nào hiệu quả nhất thì sẽ giá trị K sẽ tối ưu. Nguyên nhân là do mỗi tập dữ liệu khác nhau sẽ có các tính chất, đặc điểm khác nhau, nên khó có thể xác định được giá trị K nào là phù hợp nhất.

Về ứng dụng của thuật toán KNN phải kể đến như:

Trong y tế: xác định bệnh lý của người bệnh mới dựa trên dữ liệu lịch sử của các bệnh nhân có cùng bệnh lý có cùng các đặc điểm đã được chữa khỏi trước đây, hay xác định loại thuốc phù hợp giống ví dụ chúng tôi trình bày ở trên.

Trong lĩnh vực ngân hàng: xác định khả năng khách hàng chậm trả các khoản vay hoặc rủi ro tín dụng do nợ xấu dựa trên phân tích Credit score; xác định xem liệu các giao dịch có hành vi phạm tội, lừa đảo hay không.

Trong giáo dục: phân loại các học sinh theo hoàn cảnh, học lực để xem xem cần hỗ trợ gì cho những học sinh ví dụ như hoàn cảnh sống khó khăn nhưng học lực lại tốt.

Trong thương mại điện tử: phân loại khách hàng theo sở thích cụ thể để hỗ trợ personalized marketing hay xây dựng hệ thống khuyến nghị, dựa trên dữ liệu từ website, social media.

Trong kinh tế nói chung: giúp dự báo các sự kiện kinh tế trong tương lai, dự báo tình hình thời tiết trong nông nghiệp, xác định xu hướng thị trường chứng khoán để lên kế hoạch đầu tư thích hợp.

Còn nhiều ứng dụng khác của KNN nhưng trong bài viết này chúng tôi chỉ thể hiện cho các bạn ứng dụng phổ biến nhất của KNN đó chính là giúp các tổ chức tài chính, ngân hàng phân tích rủi ro tín dụng của khách hàng.

Ví dụ sau dưới đây là ví dụ đơn giản nhất để trình bày đến các bạn một cách dễ hiểu nhất hướng tiếp cận của KNN trong ngành ngân hàng mà thôi, nhưng thực tế thì không phải như vậy và phức tạp hơn rất nhiều và cụ thể trong lĩnh vực Data mining ứng dụng trong các tổ chức tài chính, các chuyên gia thường sử dụng những model phân tích tinh vi, kết hợp nhiều thuật toán cùng lúc hay sử dụng đa dạng các phương pháp đánh giá khác nhau để cải tiến mô hình chứ không chỉ sử dụng mỗi KNN.

Những lý thuyết chúng tôi trình bày ở trên sẽ cụ thể hóa trong chính ví dụ này.

Giả sử một ngân hàng có một tập dữ liệu gồm 5000 khách hàng đã mở các khoản vay tiêu dùng khác nhau, sau một khoản thời gian cụ thể, ngân hàng đã xác định được có 3895 khách hàng thanh toán khoản vay đúng hạn và có 1105 khách hàng không thanh toán khoản vay đúng hạn, nếu xét nợ quá hạn là sau 3 tháng kể từ thời điểm thanh toán toàn bộ, thì các khách hàng này đang trong tình trạng nợ quá hạn. Ngân hàng sẽ tổng hợp toàn bộ dữ liệu và phân loại các khách hàng này theo có khả năng nợ xấu và không có khả năng nợ xấu.

Đặt Y là khả năng nợ xấu, với Y = 0 là không có khả năng nợ xấu, ngược lại là Y = 1

Với các biến đầu vào X_i bao gồm ví dụ các biến sau:

Giới tính (nam, nữ)
Độ tuổi
Thu nhập hàng tháng (trong ví dụ này sẽ không xét đến nghề nghiệp do quá đa dạng)
Trình độ học vấn
Tình trạng hôn nhân
Tình trạng sở hữu bất động sản
Khoản vay
Thời hạn vay (tháng)

Giả định là lãi suất là như nhau đối với các khoản vay tiêu dùng (vay thế chấp)

Nhân viên ngân hàng lấy mẫu 15 khách hàng đã được phân loại khả năng nợ xấu để phân tích cho một khách hàng mới mở khoản vay.

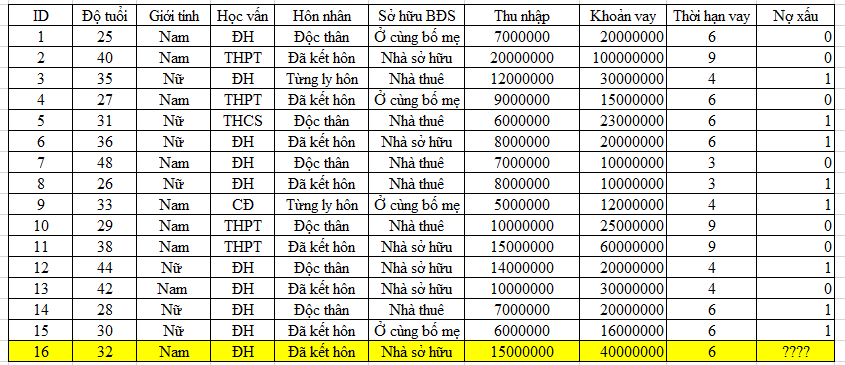
Chúng ta chuẩn hóa dữ liệu định lượng theo phương pháp Min – max để có được bảng dữ liệu như sau:

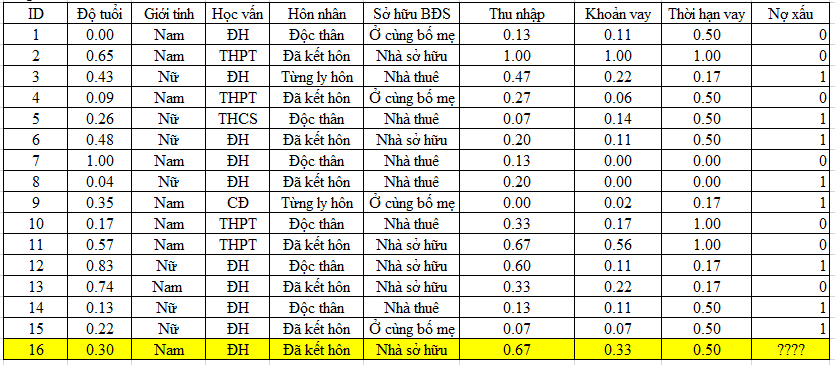
Tiếp theo chúng ta sẽ tính khoảng cách giữa các điểm dữ liệu

ví dụ d (ID 16, ID 1) = căn bậc hai của (0.3 – 0)² + 0² + 0² + 1² + 1² + (0.67 – 0.13)² + (0.33 – 0.11)² + (0.5 – 0.5)² = 1.557

Lưu ý ở các biến định tính, nếu giá trị bằng nhau thì sẽ là 0, ngược lại là 1.

Bên trên là các giá trị khoảng cách tính được qua công thức Euclidean, và xếp hạng với khoảng cách bé nhất tức là gần nhất được xếp hạng là 1.

Nếu chọn K = 1, thì khách hàng mới có ID 16 sẽ được phân loại khả năng nợ xấu theo khách hàng ID 6 là 1, nếu K = 2, tức chọn ra 2 điểm gần nhất tức chọn ra được ID 6 và ID 11 nhưng mỗi điểm lại có 2 giá trị khả năng nợ xấu khác nhau nên không phân loại được cho ID 16, nếu K = 3 thì chúng ta chọn được 3 điểm gần nhất là ID 13, ID 11, ID 6, trong đó 2 điểm có khả năng nợ xấu là 0, vậy ID 16 được phân loại khả năng nợ xấu là 0.

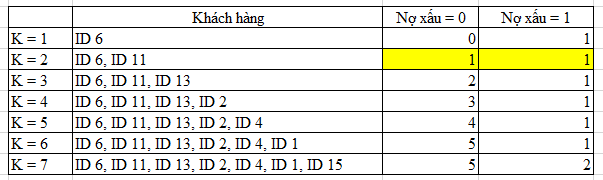
Bên trên là cách thức chọn K và giá trị vote có được cho Nợ xấu = 0, Nợ xấu = 1, ví dụ K = 7, có 7 điểm gần nhất so với ID 16 là ID 6, ID 11, ID 13, ID 2, ID 4, ID 1, ID 15, trong đó có 5 khách hàng được phân loại nợ xấu bằng 0, có 2 khách hàng được phân loại nợ xấu bằng 1. Vậy ID 16 sẽ được phân loại nợ xấu là 0.

Trong thực tế, như đã nói, việc chọn K phù hợp phải dựa trên việc chạy thử mô hình KNN với từng giá trị K khác nhau và đánh giá độ hiệu quả của từng mô hình.

Nếu chọn K = 2, thì chúng ta phải sử dụng phương pháp Weighted Voting tức tính nghịch đảo bình phương của d(ID 16, ID 6) và nghịch đảo bình phương của d(ID 16, ID 11) rồi so sánh 2 giá trị với nhau, giá trị nào lớn hơn thì ID 16 sẽ được phân loại nợ xấu theo khách hàng ấy.

Như vậy chúng tôi đã minh họa cho các bạn thấy cách thức thực hiện một thuật toán KNN đơn giản nhất ứng dụng trong ngân hàng để dự báo khả năng khách hàng mới có thể không trả kịp khoản vay đúng hạn. Tuy trong thực tế, chúng ta phải xét rất nhiều biến khác nhau tác động lên khả năng nợ xấu, và phân tích một khối lượng lớn dữ liệu, sử dụng nhiều phương pháp khác nhau để có được kết quả chính xác nhưng KNN vẫn được coi là một trong những cách tiếp cận hiệu quả.

Nếu có dịp, chúng tôi sẽ gửi đến các bạn ứng dụng mô hình KNN trong lĩnh vực khác được các chuyên gia cải tiến, hay kết hợp với các kỹ thuật phân tích khác trong Data mining. Mong các bạn tiếp tục theo dõi và ửng hộ BigDataUni.

Ở bài viết tới chúng tôi sẽ gửi đến các bạn bài viết tổng quan về các phương pháp đánh giá độ hiệu quả của các mô hình được xây dựng trên những thuật toán Classification.

Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.