Như vậy chúng ta đã đi qua 2 phần bài viết về Association rules giới thiệu về khái niệm, các ứng dụng cũng như lợi ích của phân tích, chúng ta cũng tìm hiểu qua thuật toán Apriori và hướng tiếp cận chính trong khai phá luật kết hợp.
Trong bài viết phần 3, BigDataUni và các bạn sẽ tiếp tục với thuật toán Apriori bao gồm các cách cải thiện thuật toán sử dụng Hash và các phương pháp khác nâng cao tốc độ xác định frequent itemset ở bước đầu thuật toán
Lưu ý, những bạn nào chưa biết gì vì Association rules hay Apriori thì nên đọc qua các tài liệu liên quan khác hoặc tham khảo những bài viết trước của chúng tôi về chủ đề này để nắm bắt những nội dung chúng tôi đề cập trong bài viết lần này.
Link các bài viết trước dành cho các bạn nào muốn tham khảo:
Tổng quan về Association rules (P.1)
Tổng quan về Association rules (P.2)

Nguồn hình Google
Nhắc lại một chút về thuật toán Apriori ở bài viết trước.
Lưu ý, các bạn cần phải biết trước Assocation rules là gì, thuật toán Apriori thì mới hiểu được nội dung trong bài viết này.
Hướng tiếp cận chính của hầu hết các thuật toán có trong Association rule bao gồm 2 bước:
- Tìm những itemset có tần suất xuất hiện nhiều trong tập dữ liệu, hay đạt yêu cầu Frequency > n là một số tối thiểu nào đó, nói cách khác là đáp ứng minimum Support
- Đối với mỗi itemset đạt yêu cầu frequency tìm những luật kết hợp mà ở đó có tỷ lệ Confidence cao, hoặc vượt qua ngưỡng Confidence được đặt ra.
Tại bước đầu tiên, thuật toán Apriori phát biểu định lý:
Nếu một tập phần tử hay itemset được coi là phổ biến – frequent (đạt được tỷ lệ Support tối thiểu) thì các tập con của nó – hay còn gọi subsets cũng sẽ phổ biến – frequent. Ngược lại một tập phần tử hay itemset được cho là không phổ biến – infrequent (không đạt tỷ lệ Support tối thiểu) thì các tập lớn hơn có chứa itemset này cũng sẽ infrequent.
Mục đích là ở bước 1, giảm được chi phí về mặt thời gian, giảm sự cồng kềnh trong quá trình xác định những k-itemset và tính tần số xuất hiện, frequency của mỗi k-itemset, sau đó là loại bỏ những k-itemset không đạt yêu cầu về tỷ lệ Support.
Mặc dù thuật toán Apriori đã tinh gọn bước thứ nhất bằng cách loại bỏ những k-itemset không phù hợp, tránh mất thời gian để khai phá những luật kết hợp liên quan đến những itemset này tuy nhiên việc đếm số lần xuất hiện hay frequency theo truyền thống vẫn chưa thực sự hiệu quả.
Ví dụ mà chúng ta sử dụng ở 2 bài viết trước chỉ là mẫu ví dụ nhỏ gồm 14 giao dịch mà thôi còn trong thực tế tập dữ liệu giao dịch của một công ty bán lẻ hay thương mại điện tử là rất nhiều. Do đó nếu xét từng giao dịch để tìm xem liệu có chứa 1 itemset bất kỳ nào bên trong không thì sẽ tốn nhiều thời gian, hơn nữa đâu phải chỉ có 1 itemset, thực tế sẽ rất nhiều giả sử nếu công ty có trên 100 ngành hàng khác nhau, mỗi ngành hàng sẽ ứng với 1 item, các item tạo thành nhiều itemset khác nhau nữa.
Hiện nay với nền tảng Big data và sự xuất hiện của nhiều công cụ, phần mềm phân tích dữ liệu khác nhau thì vấn đề khai phá luật kết hợp từ tập dữ liệu lớn đã dần được khắc phục nên thường chúng ta không quan tâm liệu các itemset sẽ được tính frequency như thế nào mà chỉ quan tâm đến kết quả sau cùng là những luật kết hợp tìm được.
Trong series bài viết Association rules, nghiên về lý thuyết phân tích nên chúng tôi vẫn sẽ giới thiệu đến các bạn những phương pháp cải thiện, biết đâu có khi các bạn sẽ cần dùng đến!
Ví dụ một tập các item như sau = {A, B, C, D, E} vậy giả sử có dữ liệu 1 triệu giao dịch, mỗi giao dịch sẽ chứa 2 item trở lên, chọn ra 1 itemset có 3 item từ tập trên (ví dụ {A, B, C}, {A, B, E},…), và kiểm tra trong tất cả 1 triệu giao dịch thì có bao nhiêu giao dịch chứa 3 item này? Sẽ có 5C3 (công thức tổ hợp trong toán học) = 10 tập 3-itemset tiềm năng cần kiểm tra, như vậy cần rà soát 1 triệu giao dịch tới 10 lần, tổng số giao dịch cần kiểm tra sẽ là 10 triệu. Rất phức tạp!
Ở đây chúng tôi mới ví dụ 3-itemset, trong bài viết trước chúng ta phải xác định frequency của lần lượt tất cả 1-itemset rồi đến bước loại bỏ theo tỷ lệ support tối thiểu, sử dụng kết quả từ 1-itemset suy ra 2-itemset và làm tương tự, rồi cứ như vậy làm tương tự từ 2-itemset đến 3-itemset. Do đó, tổng số lần kiểm tra tập dữ liệu sẽ nhiều!
Vậy có cách nào giúp công việc đếm – counting số lần xuất hiện của các itemset nhanh hơn, cũng như loại bỏ nhanh các itemset nếu chúng không đạt yêu cầu về tỷ lệ Support?
Dĩ nhiên là có nhưng trước khi đi vào tìm hiểu chúng ta cùng đi qua sơ lược một số yếu tố khiến cho quá trình thực hiện thuật toán Apriori phức tạp và tốn nhiều thời gian:
- Tỷ lệ Support tối thiểu: nếu chúng ta giảm tỷ lệ Support, giảm yêu cầu về tần số xuất hiện hay còn gọi Frequency sẽ khiến nhiều 1-itemset không bị loại bỏ và ở các bước sau, khi tạo ra các itemset theo kích thước k tăng dần, chúng ta sẽ test nhiều hơn trước và chắc chắn ở “vòng tuyển chọn” sau cùng sẽ có nhiều itemset đạt tiêu chí và đưa vào quá trình trích xuất những luật kết hợp => tốn nhiều thời gian hơn. Tuy nhiên liệu những luật kết hợp tìm được có đúng với thực tế khi tỷ lệ support không cao? Ví dụ nếu 1 itemset đạt tỷ lệ support giảm theo yêu cầu, thì nghĩa là có ít khách hàng mua những sản phẩm (item) trong itemset cùng với nhau. Nó đâu có phổ biến để suy ra quy luật, những item trong itemset này có thể là từ một khách hàng mua ngẫu nhiên theo nhu cầu cá nhân thì sao? Các Association rules tìm được có thể không mang giá trị hay ý nghĩa phân tích.
- Số lượng các item ban đầu: cái này chúng tôi cũng đã từng đề cập trước đó. Nếu một công ty có nhiều sản phẩm cần tìm hiểu sự kết hợp giữa chúng thì sẽ có nhiều k-itemset cần phân tích thì sẽ tốn nhiều thời gian khai phá Association rules.
- Số lượng các giao dịch: tập dữ liệu lịch sử giao dịch càng lớn thì thuật toán Apriori càng tốn nhiều thời gian khi nhiều lần kiểm tra toàn tập dữ liệu để xác định các itemset đạt yêu cầu về tỷ lệ support.
- Kích thước trung bình mỗi giao dịch: kích thước đây chính là số item trong một giao dịch. Ví dụ nếu toàn bộ các khách hàng trong tập dữ liệu chỉ giao dịch từ 1 đến 3 sản phẩm vậy k-itemset tối đa chỉ là 3-itemset, như vậy thuật toán Apriori sẽ được triển khai nhanh hơn khi tổng số itemset cần kiểm tra tỷ lệ support, cũng như khai phá Association rules sẽ ít đi, bớt phức tạp, ngược lại.
Ngoài các yếu tố từ tập dữ liệu và yêu cầu phân tích thì những phương pháp triển khai thuật toán Apriori cũng chính là nguyên nhân. Nếu các phương pháp không hiệu quả thì sẽ khiến tốn nhiều thời gian thực hiện.
Nhưng phương pháp cải thiện có thể áp dụng
- Support Counting/ Hash table/ Hash tree
Phương pháp này hướng đến phân các itemset vào những cái “xô, thùng chứa” gọi là “Bucket” sau đó thể hiện trên mô hình cây Hash hay bảng Hash. Trong quá trình đếm tần số xuất hiện, chúng ta không cần phải đối chiếu từng giao dịch với từng itemset để xem liệu có hay không itemset đó trong giao dịch ấy, và phải làm lại nhiều lần khi số lượng itemset tăng lên.
Giờ đây chúng ta có thể xác định một lúc tất cả các itemset trên một sơ đồ hay bảng, và kiểm tra từng giao dịch nếu có itemset nào trên đó thì thêm vào và tính frequency của itemset ấy sẽ + 1.
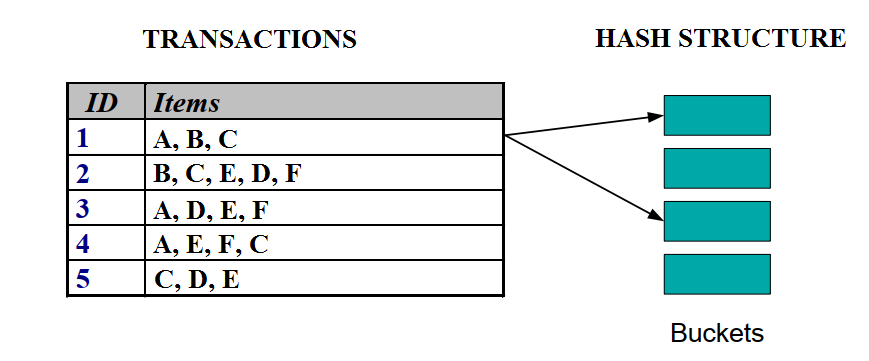
Có thể các bạn chưa hiểu nên mình cùng đi vào ví dụ cụ thể:
Cấu trúc Hash có thể triển khai theo dạng bảng và hình cây. Mỗi nhánh trong cây, hay mỗi ô, mỗi “bucket” trong bảng sẽ có công thức hay function để sắp xếp các itemset vào.
- Hash table
Giả sử chúng ta có tập dữ liệu lịch sử giao dịch của 10 khách hàng như sao:
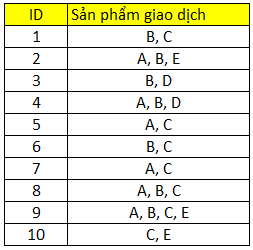
Số các item riêng biệt là 5 bao gồm A, B, C, D, E. Theo thứ tự từ trái sang phải chúng ta đánh số thứ tự từ 1 đến 5, gọi I làm tên item trước. Chúng ta có bảng dữ liệu mới như sau:
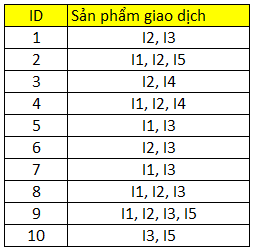
Đối với bảng Hash, chúng ta tạo các bucket, mỗi bucket sẽ mang 1 giá trị tính toán từ một function bất kỳ chúng ta đặt ra thực chất là để sắp xếp các itemset tương ứng vào mỗi bucket thuận tiện cho việc tính toán tần số, hay số lần xuất hiện.
Function của bảng Hash, ký hiệu là H. Vì tập dữ liệu trên đa số là các giao dịch có 2 item, như vậy chúng ta quan tâm các luật kết hợp khai phá từ các 2-itemset.
Ví dụ H(x, y) = (thứ tự của item thứ nhất x * 10 + thứ tự của item thứ hai y)/ 7
H(x, y) là số dư từ phép tính chia ở trên.
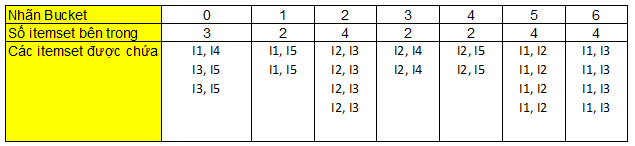
Các bạn xem qua bảng ở trên nhãn bucket chính là các số dư từ function Hash ở trên. Ví dụ giá trị 0 nghĩa là khi thay số thứ tự x, và y vào phép tính chúng ta chia hết cho 7, 1 nghĩa là chia cho 7 dư 1, tương tự 2, 3, 4, 5, 6 cũng vậy
Ví dụ: H(x, y) = (2*10 + 4)/7 = 3 dư 3, 2 và 4 chỉ item thứ 2 I2, item thứ 4 I4, như vậy 2-itemset= {I2, I4} của giao dịch có ID là 3 thỏa yêu cầu, xếp vô Bucket 3.
Các bạn xét từ giao dịch đầu tiên đến cuối cùng, đối với các giao dịch có nhiều hơn 2 item thì cần kiểm tra các 2-itemset đầy đủ, tránh bỏ sót. Ví dụ ID (2) = {(I1, I2), (I2, I5), (I1, I5)}
Như các bạn thấy khi chúng ta xây dựng bảng Hash thì công việc xác định những itemset phổ biến đạt tỷ lệ support sẽ nhanh chóng hơn, trong ví dụ này chúng ta chỉ kiểm tra toàn bộ tập dữ liệu 1 lần duy nhất là tìm được ngay kết quả frequency của tất cả itemset.
Giả sử tỷ lệ support tối thiểu trong ví dụ này là 40%, tức frequency tối thiểu là 4, mỗi itemset phải xuất hiện 4 lần ít nhất.
Do đó, trên bảng chúng ta có thể loại Bucket 0, Bucket 1, 3, 4. Itemset đạt yêu cầu frequency sẽ là {I2, I3}, {I1, I3}, {I1, I2}
- Hash tree
Phương pháp Hash tree thì phức tạp hơn một chút. Ví dụ chúng tôi tham khảo từ tài liệu “Introduction to Data mining” – Pearson, tác giả Tan, Steinbach, Kumar.
Giả sử chúng ta có 15 3-itemset, mỗi itemset sẽ chứa 3 phần tử, lấy ra từ một tập dữ liệu lịch sử giao dịch: {1 4 5}, {1 2 4}, {4 5 7}, {1 2 5}, {4 5 8}, {1 5 9}, {1 3 6}, {2 3 4}, {5 6 7}, {3 4 5}, {3 5 6}, {3 5 7}, {6 8 9}, {3 6 7}, {3 6 8}
Chúng ta sẽ xây dựng cây Hash với function như sau:
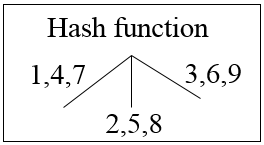
Các số 1, 4, 7 khi chia cho 3 sẽ đều có số dư là 1, tương tự 2, 5, 8 có cùng số dư là 2, và 3, 6, 9 không có số dư, hay cùng số dư là 0.
Bậc 1 sẽ bắt đầu với 1, 4 và 7; 2, 5 và 3, 6, và 9. Theo thứ tự 1,4 ,7 bên nhánh trái, 2, 5, 8 sẽ ở nhánh giữa, 3,6, 9 sẽ ở nhánh ngoài cùng bên phải
Như vậy theo 15 3-itemset ở trên, thì {1 4 5}, {1 2 4}, {4 5 7}, {1 2 5}, {4 5 8}, {1 5 9}, {1 3 6} sẽ thuộc nhánh bên trái, {2 3 4}, {5 6 7} thuộc nhánh giữa, {3 4 5}, {3 5 6}, {3 5 7}, {6 8 9}, {3 6 7}, {3 6 8} thuộc nhánh chính ngoài cùng bên phải.
Mỗi nhánh chỉ chứa tối đa 1 hoặc 2 itemset. Các bạn nhìn vào sơ đồ Hash dưới đây:
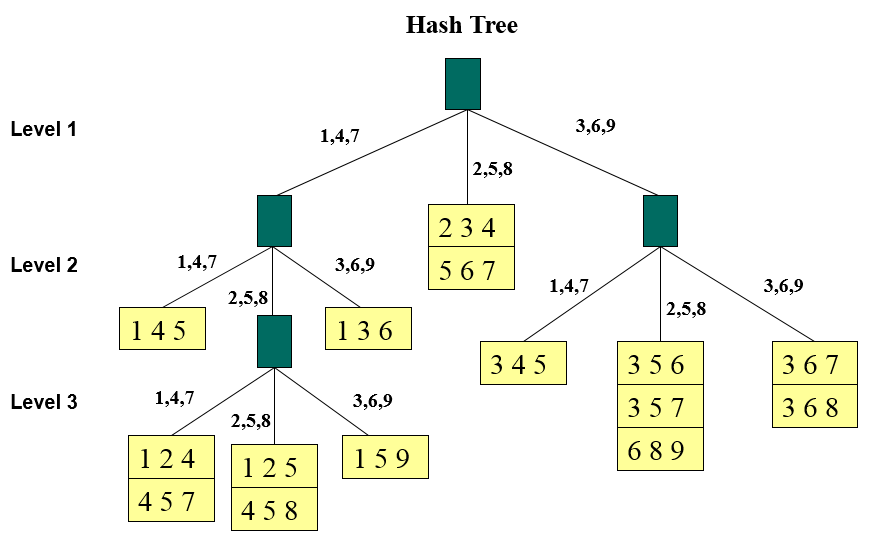
Cách làm như sau, chúng ta xét từng itemset trong 15 itemset ở trên:
Với những itemset bắt đầu là 1, 4 thì không thể để vào 1 nhánh do quá nhiều, nên tại node xanh đầu tiên, ngoài cùng bên trái ta phải phân ra 3 nhánh nhỏ, xuống bậc thứ 2. Lưu ý, các nhánh nhỏ được phân phải có function giống 3 nhánh chính, chỉ khác cấp bậc.
Mỗi nhánh đi xuống sẽ ứng với 1 item, nhánh cuối cùng sẽ ứng với item thứ 3 trong itemset.
Khá khó hiểu phải không giờ chúng tôi sẽ làm mẫu thử:
1, 4, và 7 thì ở bậc 1 tất cả các itemset bắt đầu với item 1, 4 và 7 sẽ nằm bên phía bên trái. Ở bậc 1, thì nhánh sẽ thể hiện item đầu tiên của itemset, ở bậc 2 sẽ là item thứ 2 của itemset, tương tự nếu xuống bậc thứ 3.
Ví dụ {1 4 5}, bậc 1 có item 1 bên trong, xuống bậc 2 có item tiếp theo là item 4, mà item 4 thuộc nhánh 1, 4, 7, nên chúng ta có {1 4 5} nằm ở vị trí như trên sơ đồ
Tiếp tục {1 2 4}, {4 5 7}, {1 2 5}, {4 5 8}, {1 5 9}, ở bậc 1 sẽ là nhánh trái ngoài cùng, xuống bậc 2 sẽ là nhánh giữa do các bạn thấy những item chúng tôi gạch chân đều thuộc nhánh 2, 5, 8. Tuy nhiên 1 nhánh không thể chứa quá nhiều itemset nên chúng ta phải phân ra tiếp xuống bậc thứ 3.
Tại bậc 3, {1 2 4}, {4 5 7} sẽ nằm ở nhánh 1, 4, 7 bên trái, {1 2 5}, {4 5 8} sẽ nằm ở nhánh giữa 2, 5, 8. Còn lại {1 5 9} ở nhánh bên phải ngoài cùng 3, 6, 9. Các bạn xem item gạch chân thì sẽ hiểu.
Các bạn làm tương tự cho các itemset còn lại thì sẽ hiểu sơ đồ, quan trọng là phải tuân theo thứ tự item trong mỗi itemset và đối chiếu với các nhánh ở mỗi cấp bậc.
Như vậy nếu xét các giao dịch tiếp theo, chúng ta cũng sẽ đưa vào sơ đồ Hash. Nếu 1 itemset trên sơ đồ trùng với 1 tập con trong mỗi giao dịch bất kỳ, thì Frequency + 1, tỷ lệ support sẽ tăng dần khi xuất hiện trùng lặp nhiều.
Tuy nhiên phức tạp ở chỗ, nếu giao dịch có chứa nhiều hơn 3 item, cho m > 3, thì chúng ta phải xét đến mC3 (công thức tổ hợp) số 3-itemset và đưa chúng vào sơ đồ bằng cách sắp xếp những 3-itemset theo thứ tự item.
Để minh họa rõ hơn, giả sử chúng ta có 1 giao dịch t = {1, 2, 3, 5, 6}, nếu tìm tất cả 3-itemset thì chúng ta cũng dễ dàng tìm được, nhưng khi đưa vào sơ đồ Hash tree chúng ta dễ bị rối nên cần có sự sắp xếp và phân cấp như sau:
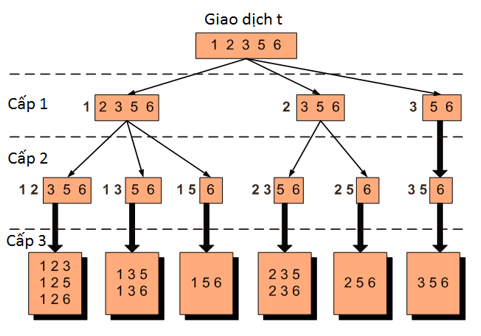
Các item trong t đã được sắp xếp theo thứ tự từ bé đến lớn. Các bạn xem lại sơ đồ Hash tree ở trên sẽ hiểu được cách phân cấp ở đây.
Ví dụ 1 + (2, 3, 5, 6) cấp 1 nghĩa là các itemset bắt đầu với item 1 sẽ ở phía bên trái, ở phía nhánh chính 1, 4, 7 bậc 1. Tại bậc thứ 3 trên sơ đồ sẽ là vị trí của {1 2 3}, {1 2 5}, {1 2 6}, {1 3 5}, {1 3 6}, {1 5 6}, cụ thể ở nhánh nào thì chúng ta phải làm từng bước như ở trên.
Kết quả mẫu như sau:
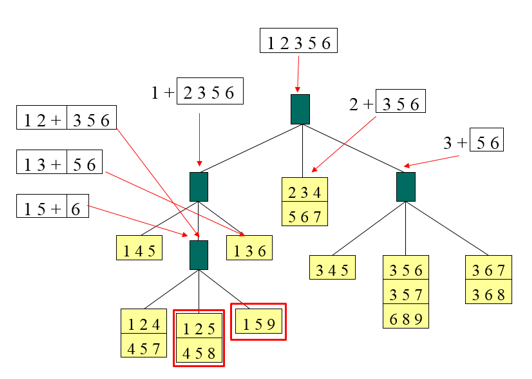
Các bạn so sánh cái itemset trong transaction ở trên với các itemset đã được xếp trên sơ đồ Hash. Ví dụ trong giao dịch t ở trên có các tập con {1 3 6}, {3 5 6}, {1 2 5} giống với 3 trong số 15 itemset trên sơ đồ. Frequency của mỗi 3 tập con này sẽ + 1
Điều quan trọng ở đây là các subset, các itemset trong giao dịch t khi đưa vào sơ đồ Hash để so sánh thì chúng ta cần các định những itemset trên sơ đồ mà chúng có thể đối chiếu.
Ví dụ 1 2 + [3, 5, 6] => {1 2 3}, {1 2 5}, {1 2 6}. Thì với item 1 sẽ đi từ nhánh bên trái đầu tiên, item 2 thì đi tiếp xuống nhánh giữa ở dưới, 3 và 6 thì ở nhánh bên phải cuối cùng phía dưới. Như vậy {1 2 3}, {1 2 6} sẽ đối chiếu với {1 5 9} do cả 3 cái này sẽ cùng vị trí. Còn 5 thì ở nhánh giữa cuối cùng phía dưới {1 2 5} sẽ đối chiếu với {1 2 5} và {4 5 8}. Duy chỉ có {1 2 5} là giống nhau mà thôi. Đến lượt các bạn làm thử so sánh các itemset còn lại của giao dịch t. Lưu ý các bạn phải luôn nhớ Hash function.
- Phương pháp Hash như các bạn có thể thấy thì đã đơn giản bước 1 của thuật toán Apriori đi rất nhiều, thay vì ở bài viết trước chúng ta xác định frequency, kiểm tra tỷ lệ support của 1-itemsets đến 2-itemsets rồi mới đến 3-itemsets kết hợp định luật phát biểu bởi thuật toán, thì phương pháp Hash cho chúng ta tìm ngay các k-itemset quan tâm và đảm bảo yêu cầu về tỷ lệ support mà không cần kiểm tra nhiều lần toàn tập dữ liệu.
Bên cạnh Hash chúng ta cũng còn nhiều cách cải thiện bước 1 của thuật toán Apriori như sử dụng sơ đồ Lattice (chúng tôi đã từng giới thiệu qua bài viết trước). Do bài viết có giới hạn nên chúng tôi không thể trình bày cụ thể, các bạn có thể tham khảo thêm ở những tài liệu khác.
Những phương pháp khác giúp cải thiện thuật toán Apriori:
- Giảm các giao dịch khi có thể
Nếu chúng ta phải kiểm tra lại tập dữ liệu nhiều lần để tìm những itemsets đạt yêu cầu về tỷ lệ support như theo cách truyền thống (chưa nói đến Hash hay Lattice), thì vẫn có cách rút ngắn thời gian bằng việc loại bỏ những giao dịch không cần phân tích, số lượng các giao dịch sẽ giảm dần từ các lần kiểm tra tập dữ liệu lúc sau. Một giao dịch không có chứa bất kỳ k-itemset nào đạt yêu cầu về tỷ lệ Support hay Frequency tối thiểu thì cũng sẽ không chứa (k+1)-itemset đạt yêu cầu về tỷ lệ Support hay Frequency tối thiểu. Ví dụ. t= {2, 4, 6} mà {2, 4} có tỷ lệ Support nhỏ hơn tối thiểu thì giao dịch t này cần được đánh dấu và loại bỏ trước khi kiểm tra tập dữ liệu để tìm tiếp các 3-itemset. Do {2, 4} ít phổ biến trong tập dữ liệu thì cho dù có thêm vô 6 cũng sẽ như vậy, {2, 4, 6} sẽ không được tính nên bước sau kiểm tra lại lần nữa thì không cần thiết
Như vậy nghĩa là, ở cách truyền thống, chúng ta chỉ loại bỏ những itemset không đạt yêu cầu để giai đoạn sau không cần quan tâm chúng, thì ở phương pháp này chúng ta sẽ bỏ trước luôn các giao dịch có max size = k + 1 (số item bên trong), tập con k-itemset không đạt yêu cầu về tỷ lệ support, mà (k+1) itemset là những itemset được kiểm tra tỷ lệ support ở bước ngay kế tiếp.
- Phân chia tập dữ liệu
Chia tập dữ liệu thành 2 phần dữ liệu, mỗi phần dữ liệu sẽ chỉ cần kiểm tra 1 lần qua đó sẽ giảm bớt số lần quét tập dữ liệu để xác định các itemset đạt yêu cầu về tỷ lệ Support.
- Gọi D là tập dữ liệu lớn. Đầu tiên, tập dữ liệu D sẽ được chia thành n phần dữ liệu nhỏ hơn không trùng lặp nhau, n tối thiểu có thể là 2.
- Xác định tỷ lệ support mong muốn cho các itemset trên toàn tập dữ liệu D. Như vậy các itemset chọn ra trong mỗi phần dữ liệu sẽ cần có frequency tối thiểu = tỷ lệ support * số quan sát bên trong phần dữ liệu.
- Trong mỗi phần dữ liệu, chọn ra những itemset đạt frequency tối thiểu được tính ở bước trên. Các itemset đạt tỷ lệ support trong mỗi phần dữ liệu có thể không đạt tỷ lệ support nếu xét trên toàn bộ tập dữ liệu D. Theo nguyên tắc đã được chứng minh tham khảo từ tài liệu “Data mining – Concepts and Techniques” của tác giả Jiawei Han và cộng sư:
- Nhưng nếu một itemset được coi là phổ biến, đạt tỷ lệ support xét trên toàn tập dữ liệu D thì nó ít nhất phải đạt yêu cầu về frequency tối thiểu ở một trong các phần dữ liệu. Từ đó suy ra, tất cả các itemset đạt yêu cầu được lấy ra từ các phần dữ liệu cũng sẽ là các itemset tiềm năng của tập dữ liệu D cho giai đoạn sau..
- Tính toán lại tỷ lệ support những itemset đó nhưng xét trên toàn tập dữ liệu D chúng ta sẽ có được các itemset tối ưu để tìm ra các luật kết hợp
Lấy mẫu
Lấy mẫu S ngẫu nhiên từ tập dữ liệu lớn, sau đó tìm các itemset đạt yêu cầu về tỷ lệ support trên mẫu đó thay vì tập dữ liệu D. Chúng ta có thể tăng độ hiệu quả, giảm được thời gian nhưng có thể bỏ sót các itemset đạt yêu cầu về tỷ lệ support khác nằm ngoài mẫu, (phần còn lại của tập D, sau khi mẫu được lấy đi). Để khắc phục vấn đề, chúng ta sử dụng tỷ lệ support tối thiểu trong dữ liệu mẫu < tỷ lệ support tối thiểu của toàn tập D.
Các itemset đạt yêu cầu về tỷ lệ support trong mẫu dữ liệu gọi là FS . Những itemset trong Fs lần nữa sẽ được tính Frequency, tần số xuất hiện thực tế dựa trên dữ liệu còn lại trong tập D. Vì tỷ lệ support tối thiểu của Fs < của tập D, nên khả năng Fs chứa tất cả các itemset đạt tỷ lệ support của toàn tập D (cũng là các itemset cần tìm ở bước 1 được đưa vào quá trình khai phá luật kết hợp) là khá cao.
Nếu có, thì chúng ta chỉ kiểm tra toàn tập dữ liệu D 1 lần duy nhất để xác định tỷ lệ support chính xác nhất cho các itemset. Nếu không, thì phải xem lại ở Fs có thiếu itemset nào đạt tỷ lệ support tối thiểu mà bị bỏ sót hay không.
- Đếm số lần xuất hiện của các itemset chủ động
Phương pháp này áp dụng cho tập dữ liệu giao dịch được chia thành nhiều khối và mỗi khối đều có các điểm bắt đầu, có các mốc. Khi chúng ta kiểm tra tập dữ liệu theo trình tự các khối để tính tần số các itemset thì những itemset nào có tần số tăng dần thì được coi là tiềm năng và được thêm vào (note lại) tại các điểm bắt đầu.
Khác với thuật toán Apriori khi các itemset mới chỉ tìm được khi kết thúc kiểm tra cả tập dữ liệu về tần số, tỷ lệ support của các itemset trước đó. Còn tại phương pháp này những itemset mới, tiềm năng có thể tìm được mà chưa cần xét đến hết tập dữ liệu, đồng thời cũng không cần kiểm tra tập dữ liệu thêm lần nào nữa.
Các itemset khi tần số đếm được tăng dần qua các khối và khi vượt frequency tối thiểu hay tỷ lệ Support tối thiểu thì sẽ được đưa vào tập hợp F bao gồm những itemset đạt yêu cầu về kích thước k, về tỷ lệ support chuẩn bị đưa vào giai đoạn khai phá luật kết hợp
Để cải thiện thuật toán Apriori nói riêng hay quy trình khai phá luật kết hợp nói chung còn rất nhiều phương pháp khác và cả các thuật toán khác như Maximal & closed itemset, Toivoven, FP- Growth,… do bài viết có giới hạn nên chúng tôi không thể trình bày hết ở series Association rule lần này mà hẹn các bạn ở những series khác.
Đến đây là kết thúc bài viết phần 3, ở phần 4 cuối cùng chúng ta sẽ đi vào các phương pháp đánh giá luật kết hợp khác
Tài liệu tham khảo:
“Introduction to Data mining” – Pearson, tác giả Tan, Steinbach, Kumar
“Data Mining Concepts and Techniques” – Jiawei Han, Micheline Kamber, Jian Pei
“Data mining and predictive analytics” – Daniel T. Larose
“Principles of Data mining” – Max Bramer
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English