Ở bài viết trước về hồi quy logistic (logistic regression), chúng ta đã tìm hiểu về khái niệm hồi quy logistic là gì, ứng dụng của nó, cũng như khi nào là thích hợp để áp dụng vào phân tích dữ liệu. Bên cạnh đó, BigDataUni cũng giới thiệu đến các bạn phương trình tổng quát của hồi quy logistic, đồ thị, giải thích các hệ số và đi vào ví dụ đơn giản nhất đầu tiên.
Dành cho bạn nào chưa xem qua phần 1 bài viết, lưu ý trong bài viết này chúng tôi sẽ không đề cập lại chi tiết nội dung ở bài viết trước.
Tổng quan về Logistic regression (P.1)
Đến với phần 2 bài viết, BigDataUni và các bạn sẽ nghiên cứu chi tiết về phương trình tổng quát của hồi quy logistic, ý nghĩa của các hệ số, ý nghĩa của kết quả thu được từ phương trình hay nói cách khác giải thích phương trình. Bên cạnh đó chúng ta cũng sẽ đi sang ví dụ khác để hiểu rõ hơn. Bài viết có tham khảo một phần lý thuyết trong tài liệu quốc tế “Statistics for Business and Economics” phiên bản 13, của nhà xuất bản Cengage Learning
Nhắc lại một số điểm quan trọng ở phần 1
Logistic regression là phương pháp hồi quy thông dụng nhất, áp dụng cho các biến mục tiêu không phải là biến định lượng liên tục (continuous variable). Trong bài viết phần 2 và ở những bài viết tới chúng ta sẽ tập trung vào hồi quy logistic áp dụng cho biến thay phiên. Logistic regression được ứng dụng để dự báo và phân loại giá trị của biến mục tiêu dựa trên dữ liệu của các biến đầu vào ví dụ dự báo khả năng khách hàng rời dịch vụ (biến mục tiêu y chỉ có 2 giá trị có rời dịch vụ, chưa rời dịch vụ), phân loại khách hàng có khả năng trả nợ để cấp phát thẻ tín dụng (biến mục tiêu y chỉ có 2 giá trị: có hoặc không có khả năng trả nợ).
Công thức tổng quát của hồi quy logistics đơn biến
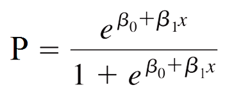
Khác với hồi quy tuyến tính, kết quả của phương trình hồi quy logistic là xác suất và dựa vào xác suất để quyết định giá trị sau cùng của biến y. Đối với hồi quy logistic, biến y chỉ có 2 giá trị ví dụ như có và không, thành công và thất bại, sống sót và chết, còn sử dụng dịch vụ và không còn sử dụng dịch vụ thông thường theo thông lệ các chuyên gia phân tích sẽ gán y = 0 cho các kết quả “không”, “thất bại”, “chết”, “rời dịch vụ”, còn gán y = 1 cho giá trị còn lại
Với p là biến phụ thuộc, xác suất khả năng y xảy ra 0 hoặc 1 (chịu ảnh hưởng của biến x), là biến chúng ta sẽ dự báo giá trị, x là biến độc lập (biến tác động lên biến phụ thuộc), β0 là giá trị ước lượng cho p khi x đạt giá trị 0, β1 dùng để xác định giá trị trung bình của p tăng hay giảm khi x tăng.
Trong thực tế khi phân tích chúng ta sẽ quan tâm nhiều hơn đến tất cả các yếu tố liên quan đến đối tượng mục tiêu nghiên cứu, khi ấy phương trình tổng quát:
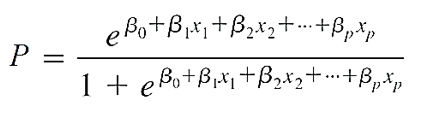
Logistic regression được úng dụng trong nhiều ngành và lĩnh vực khác nhau, một số ví dụ như:
- Dự báo hay phân loại email có phải spam hay không spam
- Dự báo khả năng rời dịch vụ của khách hàng
- Dự báo tình trạng khối u ung thư là ác tính hay lành tính trong y học.
- Dự báo khả năng khách hàng sẽ mua sản phẩm bất kỳ, hay đăng ký dịch vụ
- Dự báo khả năng trả nợ của khách hàng
Điểm khác biệt giữa hồi quy tuyến tính và logistic regression chính là hồi quy tuyến tính dự báo giá trị của biến mục tiêu dựa trên mối quan hệ giữa nó với các biến độc lập x. Còn hồi quy logistic hướng đến việc dự báo xác suất, khả năng biến y đạt một trong hai giá trị của nó dựa trên mối quan hệ giữa nó với các biến độc lập x. Ví dụ nếu chúng ta muốn dự báo khả năng khách hàng rời dịch vụ thì chúng ta sẽ quan tâm đến các khách hàng có khả năng cao để đưa ra những chiến lược để giữ chân. Do đó thông thường biến mục tiêu y có 2 giá trị và sẽ được gán 1 cho “rời dịch vụ” và 0 cho “không rời dịch vụ”. Vậy làm thế nào để biết được y sẽ mang giá trị nào trong 2 giá trị này?
Dĩ nhiên vì giá trị của biến y là biến định danh không phải là định lượng và việc gán giá trị 0 và 1 thứ nhất là để hướng kết quả phân tích mà mình quan tâm, thứ hai là để đơn giản hóa kết quả phân tích và khiến chúng dễ hiểu hơn, gọn hơn. Do đó sẽ không có chuyện chúng ta tính kết quả của phương trình hồi quy và tìm ngay thấy y có thể bằng 0 hay 1 vì 2 giá trị này không phải giá trị số thực trong khi đó các biến độc lập x có thể là biến định lượng. Nhưng nếu nhìn vào các biến x thì chúng có mối quan hệ nào với biến mục tiêu y không, và các mối quan hệ này có thể hiện khả năng biến y là 0 hay 1 không?
Chúng ta thường nói khả năng đi kèm với xác suất. Ví dụ đội tuyển Việt Nam có khả năng thắng đội tuyển Malaysia ở lượt về vòng loại thứ 2 World Cup hay không? Một chuyên gia bóng đá nhận định 70 – 80% Việt Nam sẽ thắng và thường sẽ không nói “tôi nghĩ Việt Nam sẽ thắng” nếu nói như vậy thì người đặt câu hỏi sẽ hỏi tiếp “cơ sở nào để đưa ra nhận định” hay “bao nhiêu % Việt Nam sẽ thắng.”
Mọi kết luận nếu không có căn cứ thì không đáng tin cậy và có thể dẫn đến hậu quả khó lường. Nếu một khách hàng lần gần nhất mua hàng là 2 tháng trước, đăng ký thẻ thành viên từ năm ngoái, tần suất mua hàng trong tháng rất thấp, thu nhập hàng tháng không cao thì bạn có dám chắc khả năng người khách hàng này đã rời dịch vụ hay không nếu chỉ dựa trên các dữ kiện này? Chúng ta cần có xác suất để khẳng định.
Vậy mô hình hồi quy logistic sẽ hướng đến tính toán, ước lượng xác suất để kết luận giá trị y chứ không phải được dùng để tìm ra giá trị sau cùng của y. Chúng tôi sẽ diễn giải phương trình hồi quy logistics để các bạn có thể hiểu rõ hơn về phương trình hồi quy logistic tổng quát.
Hiểu hơn về phương trình tổng quát logistic regression
Lưu ý trong bài viết này chúng ta chỉ quan tâm trước mắt là hiểu về phương trình tổng quát trước còn việc ước lượng giá trị của các tham số β để hình thành phương trình hoàn chỉnh như sử dụng phương pháp Maximum Likelihood Estimation (MLE) (điểm khác biệt khác giữa hồi quy logistic và hồi quy tuyến tính) chúng tôi sẽ trình bày trong các bài viết tới cùng với các phương pháp đánh giá độ hiệu quả của phương trình hồi quy Logistic trong việc dự báo.
Như đã biết thì xác suất thì phải nằm trong khoảng giá trị 0 và 1 (0% và 100%), nó không thể nhỏ hơn 0 hay lớn hơn 1. 1 là chắc chắn xảy ra, 0 là chắc chắn không xảy ra.
Để giới hạn kết quả tính toán nằm từ 0 đến 1, là xác suất của phương trình hồi quy logistic, người ta sử dụng một loại hàm trong toán học gọi là Sigmoid Function hay Logistic Function (logistic được lấy làm tên cho dạng hồi quy này) hay Logistic Transformation. Có 3 tên khác nhau nhưng cùng chung một dạng gọi là hàm Logit đảo ngược (Inverse logit function).
Chúng ta sẽ tìm hiểu trước về Logit function. Bài viết không đi sâu về các kiến thức toán học nên nếu các bạn có thắc mắc về thuật ngữ gì, công thức gì có thể nghiên cứu thêm bên ngoài. Phạm vi của bài viết chỉ tập trung vào công thức tổng quát của hồi quy logistic.
Hàm logit đơn giản là logarit của giá trị Odds. Odds, hay tỉ số của 2 xác suất, mà odds dịch sang tiếng Việt nghĩa là xác suất hay khả năng một sự sẽ xảy ra hay không xảy ra. Nếu xác suất sự kiện xảy ra là p, thì xác suất sự kiện không xảy ra chắc chắn là 1 – p.
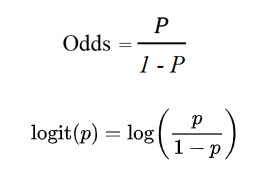
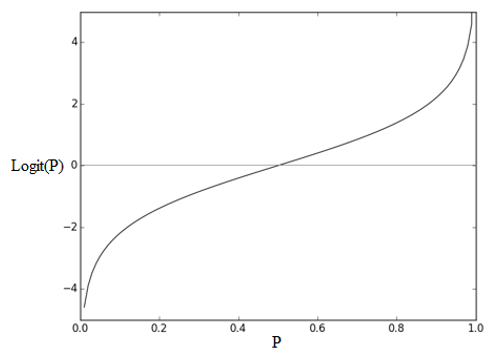
Odds ratio hay Logit function được dùng chủ yếu trong lĩnh vực thống kê mục đích để chuyển đổi giá trị xác suất trong khoảng (0; 1] thành những giá trị số thực (real numbers) nằm trong khoảng (- ∞, + ∞), nghĩa là giá trị của hàm logit sẽ tiến đến + ∞ khi xác suất p tiến đến 1, và giá trị hàm logit sẽ tiến đến – ∞ khi xác suất p tiến đến 0.
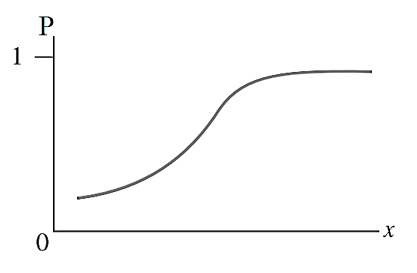
Hàm logit được sử dụng chủ yếu trong lĩnh vực thống kê (statistics) cũng như các lĩnh vực chuyên sâu về khai phá dữ liệu hay học máy vì chúng có thể chuyển đổi các dữ liệu là biến nhị phân (binary variable) sang biến định lượng với các giá trị số thực. Các bạn hãy nhìn qua đồ thị dưới đây:
Hàm Sigmoid là một dạng ngược lại của hàm logit, tức nếu chúng ta có xác suất p thì sigmoid (logit(p)) = p, nghĩa là lúc này chúng ta sẽ chuyển được các giá trị thực của một biến bất kỳ nằm trong khoảng (-∞; +∞) sang giá trị nằm trong khoảng (0, 1]. Do đó hàm Sigmoid rất hữu ích trong các bài toán phân loại Classification và đặc biệt là đối với thuật toán Neural Network, khi tính năng chính của nó phù hợp để xem xét, tính toán kết quả phân tích ở giai đoạn sau cùng của quy trình phân loại thành những kết quả cụ thể.
Công thức tổng quát của hàm Sigmoid:

Lưu ý lý thuyết về logarit và hằng số nepe các bạn có tham khảo lại kiến thức toán học phổ thông để tìm hiểu thêm, trong bài viết này chúng tôi sẽ không đề cập sâu hơn.
Các bạn cùng nhìn qua đồ thị hàm sigmoid

Hàm Sigmoid được nhận biết với đặc điểm nổi bật là độ thị của nó có hình cong như chữ S. Hàm Sigmoid thực chất bắt nguồn từ hàm Logistic – các bạn có thể hiểu hàm logistic chính là hàm gốc có đồ thị dạng hình chữ S đầu tiên hay còn gọi là đường cong Sigmoid “Sigmoid curve”, còn hàm Logit và Sigmoid giống như biến thể của hàm logistic. Và cũng chính vì thế mặc dù hàm Sigmoid được dùng trong mô hình hồi quy áp dụng cho biến mục tiêu là biến thay phiên, biến nhị phân (binary) nhưng không được gọi là Sigmoid Regression mà Logistic Regression.
Công thức hàm Logistic:
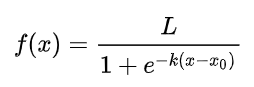
Với L là giá trị cực đại của đường cong, e là hằng số nepe, k là độ dốc của đường cong, x0 là giá trị x chiếu lên tại điểm chính giữa hay trung điểm của đường cong chiếu xuống. Nhìn vào đồ thị và công thức của hàm Sigmoid chúng ta thấy đường cong tại S(X) = 1 là cực đại nếu đối chiếu qua công thức trên thì L sẽ bằng 1, k = 1, và x0 sẽ bằng 0. Đó là lý do tại sao chúng tôi nói hàm Sigmoid là biến thể của hàm logistic.
Như vậy chúng ta đã tìm hiểu quả 3 loại hàm quan trọng giờ quay lại với Logistic regression. Phương trình tổng quát của hồi quy logistic sẽ dựa vào phương trình tổng quát của hàm Sigmoid để hình thành.
Tất cả các dạng hồi quy thực tế có cùng chung một phương trình tổng quát để chỉ ra rằng giá trị của biến mục tiêu y trong tương lai sẽ thay đổi hay biến động dựa vào mối quan hệ của nó đối với tất cả các biến độc lập x còn lại bất kể có phải là mối quan hệ tuyến tính hay phi tuyến.
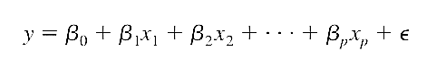
Cũng trong thực tế khi thiết lập mô hình hồi quy để dự báo và ước lượng người ta thường quan tâm đến nhiều yếu tố tác động lên đối tượng nghiên cứu hay nói cách khác muốn tìm hiểu quan hệ giữa nhiều biến độc lập x với biến mục tiêu. Chúng ta có phương trình tổng quát để ước lượng giá trị cho biến mục tiêu y (lưu ý sai số e đã được loại bỏ)
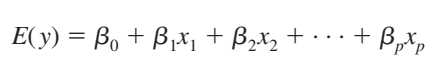
Mà E(y) trong phương trình logistic regression là xác suất để kết luận giá trị của biến y, không phải giá trị thực của biến y.
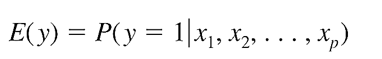
Áp dụng phương trình hàm sigmoid để chuyển đổi giá trị (β0 + β1x1 + β2x2 + …+ βpxp) (đây là phần giá x trong phương trình hàm sigmoid) thành xác suất để kết luận giá trị của biến y.
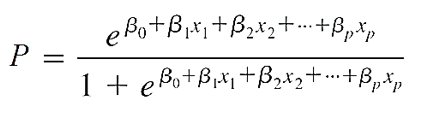
Cách diễn giải có lẽ sẽ khó hiểu và nhàm chán. Chúng ta cùng đi sang ví dụ cụ thể về ứng dụng hồi quy logistics để bài viết trở nên thú vị hơn.
Trước khi đi vào ví dụ, một điểm lưu ý nữa về Sigmoid Function là giá trị tại đó chiếu thẳng lên điểm chính giữa đường cong có thể được dùng để làm mốc kết luận giá trị của biến y, nghĩa là có thể lấy p = 0.5 làm chuẩn.
Ví dụ từ phương trình logistic regression, chúng ta có thể ước lượng xác suất có thể trả nợ của một khách hàng A là 0.75 thì khách hàng này có khả năng trả nợ được vì 0.75 > 0.5 nên biến y sẽ mang giá trị là 1 – trả nợ, ước lượng xác suất của khách hàng B là 0.4 vì 0.4 < 0.5 nên biến y sẽ mang giá trị 0 – không có khả năng trả nợ.
Tuy nhiên đó chỉ là tham khảo mà thôi, việc xác định giá trị sau cùng của biến y dựa trên xác suất còn tùy vào góc nhìn và kinh nghiệm của chuyên gia phân tích.
Ví dụ cụ thể
Ví dụ ứng dụng logistic regression vào email marketing. Một công ty bán lẻ các sản phẩm công nghệ, điện tử có các cửa hàng nằm trong 2 tỉnh thành khác nhau, công ty tháng trước đã triển khai một chương trình ưu đãi dành cho khách hàng thân thiết. Công ty đã thiết kế một email quảng cáo để gửi đến những khách hàng của mình ở tỉnh A, bao gồm những khách hàng có thẻ thành viên và những khách hàng không có thẻ thành viên. Công ty muốn phân tích xem số tiền mà mỗi khách hàng bỏ ra trong 1 năm qua và đăng ký thẻ thành viên có tác động như thế nào đến việc khách hàng tham gia chương trình ưu đãi. Chương trình ưu đãi cụ thể là nhận phiếu giảm giá 25%, khi tổng giá trị hàng mua là trên 5 triệu. Lấy mẫu 100 khách hàng thì có 40 khách hàng tham gia bằng cách click vào link đăng ký trong email, 60 khách hàng còn lại thì không. Công ty muốn dự báo hay phân loại một nhóm khách hàng ở cửa tỉnh B có khả năng đăng ký chương trình ưu đãi hay không nếu dựa vào kết quả phân tích để quyết định tháng tới có làm chương trình tương tự hay không.
Như vậy trước tiên chúng ta sẽ xây dựng phương trình hồi quy logistic sử dụng dữ liệu lịch sử để phân tích khả năng khách hàng mới có khả năng đăng ký chương trình ưu đãi hay không. Biến mục tiêu là khả năng đăng ký chương trình ưu đãi với y = 1 – sẽ đăng ký chương trình, y = 0 – không đăng ký chương trình. Biến độc lập x1 là số tiền khách hàng bỏ ra trong năm vừa rồi. Biến độc lập x2 là thông tin về đăng ký thẻ thành viên, x2 = 1 là có thể thành viên, x2 = 0 là không có thể thành viên.
Lưu ý nếu các bạn nào có theo dõi toàn bộ những bài viết về linear regression có lẽ sẽ thắc mắc tại sao chúng tôi chưa đề cập đến trường hợp biến độc lập là biến định tính, biến định danh mà không phải biến định lượng thì khi xây dựng phương trình hồi quy thì như thế nào? Cụ thể là chúng tôi muốn làm rõ sự khác biệt trong cách xử lý nếu biến y là biến định tính hay một trong các biến x là biến định tính, vì vậy để trường hợp này lại và trình bày trong series bài viết về hồi quy logistic. Trong bài viết về ứng dụng hồi quy logistic, chúng tôi sẽ gửi đến các bạn một ví dụ chi tiết về phương trình hồi quy linear regression có biến độc lập là biến định tính.
Chúng ta có phương trình tổng quát logistic regression:
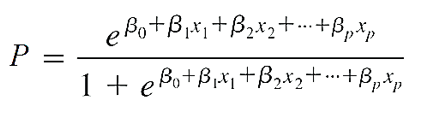
Đầu tiên chúng ta sẽ xây dựng phương trình hồi quy logistic tổng quát cho ví dụ trên. Các bạn có thể sử dụng các phần mềm thống kê hay phân tích dữ liệu khác nhau để thực hiện tìm phương trình logistic regression. Do công thức tổng quát sử dụng hằng số nepe cũng như công thức logarith nên việc tính toán để tìm ra các giá trị của các hệ số hồi quy là rất phức tạp, chúng ta thường sử dụng phần mềm.
Tập dữ liệu mẫu 100 khách hàng, 30 quan sát mẫu như sau
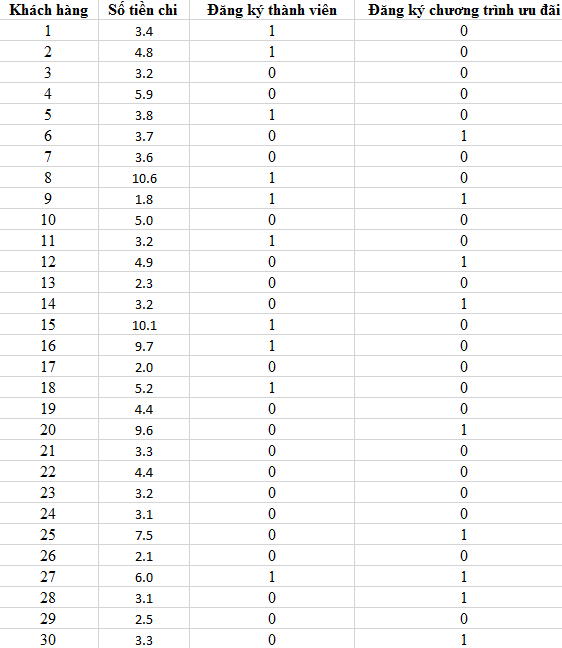
Các bạn có thể tải data theo link google drive tại đây.
Lưu ý số tiền chi tính bằng đơn vị triệu VND
Chúng tôi sử dụng phần mềm spss statistics để thực hiện tìm ra phương trình hồi quy logistic và kết quả có được như sau:
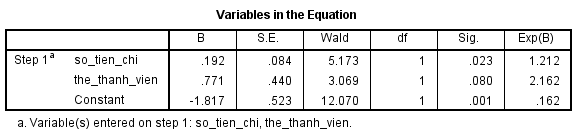
Phương trình dùng để ước lượng xác suất thể hiện khả năng khách hàng có thể đăng ký chương trình ưu đãi:
E(y) = P = (e(-1.817 + 0.192*x1 + 0.771*x2))/ (1 + e(-1.817 + 0.192*x1 + 0.771*x2))
Các bạn chú ý trước đến cột B vì cột này thể hiện giá trị cần tìm của các hệ số hồi quy, các cột còn là gì chúng tôi sẽ nói ở bài viết tới khi trình bày về phương pháp kiểm định, đánh giá độ hiệu quả.
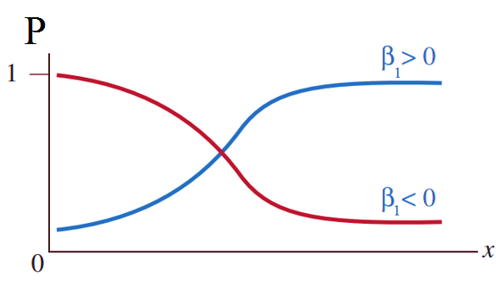
Giải thích một chút về hệ số hồi quy. Hệ số hồi quy dùng để xác định giá trị trung bình của p tăng hay giảm khi x tăng. Tham số β trong mô hình thể hiện giá trị trung bình của p tăng hay giảm khi x tăng. Khi β1 > 0, xác suất p tăng khi x tăng. Khi β1 < 0, xác suất p giảm khi x tăng. Nếu β1 = 0, p không thay đổi khi x thay đổi, lúc này đường cong sẽ biến thành một đường thẳng nằm ngang. Độ dốc của đường cong tăng khi giá trị tuyệt đối của β1 tăng. Các bạn có thể xem lại đồ thị mà chúng tôi đề cập đầu bài viết.
Với hệ số hồi quy β1 = 0.192 > 0 vậy khi số tiền một khách hàng chi trong năm càng tăng lên thì khả năng khách hàng đăng ký tham gia chương trình ưu đãi càng cao, vì x1 tăng thì p sẽ tăng. Tuy nhiên vì x2 là biến định tính nên chỉ có 2 giá trị 0 và 1 gán cho “chưa đăng ký thẻ thành viên” và “đăng ký thẻ thành viên” nên chúng ta khó có thể kết luận tương tự mặc dù hệ số hồi quy β2 cũng > 0. Do đó chúng ta cùng ước lượng thử để so sánh xác suất khả năng khách hàng đăng ký chương trình nếu có thẻ thành viên rồi so với xác suất khả năng khách hàng đăng ký chương trình mà chưa có thẻ thành viên.
Trường hợp 1 khách hàng có thẻ thành viên, số tiền chi ra trong năm ngoái là 3 triệu.
E(y1) = P1 = ((e(-1.817 + 0.192*3 + 0.771*1))/ (1 + e(-1.817 + 0.192*3 + 0.771*1)) = 0.385
Trường hợp 1 khách hàng không có thẻ thành viên, số tiền chi ra trong năm ngoái là 3 triệu.
E(y1) = P1 = ((e(-1.817 + 0.192*3 + 0.771*0))/ (1 + e(-1.817 + 0.192*3 + 0.771*0)) = 0.224
- Khách hàng có thẻ thành viên có khả năng đăng ký chương trình ưu đãi hơn so với không có thẻ thành viên.
Các bạn có thể tiếp tục thêm các trường hợp để ước lượng thử xác suất cho quen nhé.
Nếu lấy p = 0.5 làm chuẩn thì cả 2 trường hợp trên không thể xếp loại khách hàng vào nhóm có khả năng đăng ký chương trình ưu đãi vì xác suất ước lượng đều thấp hơn 0.5.
Như vậy công ty dựa vào kết quả phân tích có thể quyết định khách hàng nào mình nên gửi email marketing hay thúc đẩy các hoạt động tư vấn, chăm sóc khách hàng để lôi kéo họ đăng ký chương trình ưu đãi. Việc làm rất đơn giản là chúng ta sẽ xây dựng các mốc số tiến chi năm ngoái, mỗi mốc sẽ có xác suất ước lượng tương ứng, và ưu tiên khách hàng có thẻ thành viên.
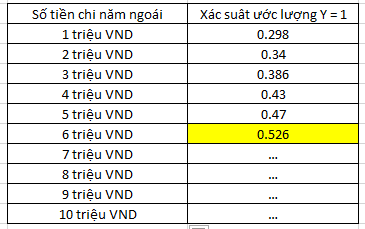
Như đã nói vì hệ số hồi quy β1 = 0.192 > 0 nên p sẽ tăng khi số tiền chi tăng. Ở mốc 6 triệu, các bạn có thể thấy xác suất đã vượt ngưỡng 0.5 cho thấy khách hàng nào có thẻ thành viên và số tiền chi trong năm ngoái mua hàng công ty trên 6 triệu thì nhiều khả năng đăng ký chương trình ưu đãi.
Đến đây là kết thúc bài viết phần 2 về logistic regression. Mong các bạn tiếp tục ủng hộ BigDataUni trong những bài viết sắp tới.
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English