Ở các bài viết trước chúng ta đã tìm hiểu về ứng dụng hồi quy tuyến tính trong lĩnh vực bán lẻ, từ lý thuyết đến triển khai các ví dụ cụ thể cũng như bàn luận về những vấn đề liên quan như đa cộng tuyến, và phương pháp đánh giá độ hiệu quả của mô hình hồi quy tuyến tính. Trong bài viết tuần này và các bài viết sắp tới chúng ta sẽ đi vào tìm hiểu một dạng hồi quy khác, cũng rất phổ biến không chỉ trong lĩnh vực thống kê mà còn ở lĩnh vực khai phá dữ liệu – Data mining, có nhiều ứng dụng trong kinh tế, khoa học và xã hội. Bài viết phần 1 chúng ta sẽ tìm hiểu về hồi quy logistic regression là gì, điểm khác biệt với các loại hồi quy khác, mục đích sử dụng, phương trình và đồ thị tổng quát, và đi vào ví dụ đơn giản đầu tiên.
Hồi quy từ lâu đã trở thành một phần không thể thiếu trong Data analysis liên quan đến việc tìm hiểu và phân tích mối quan hệ giữa các đối tượng nghiên cứu thể hiện qua biến mục tiêu (biến y) và các biến độc lập (biến giải thích – các biến x). Vì các đối tượng nghiên cứu thường đa dạng và khác nhau về bản chất khiến cho loại biến, hay loại dữ liệu sẽ khác nhau. Cụ thể chúng ta có các dạng biến sau. Các bạn có thể xem lại bài viết về Statistics của BigDataUni để hiểu chi tiết hơn:
Tổng quan về Statistics: Descriptive statistics (thống kê mô tả)
Biến (hay dữ liệu) thường có 2 dạng chính là định tính (qualitative/categorical variable), định lượng (quantitative/numerical variable), và biến nhị phân (binary variable).
Biến định tính hay biến phân loại là biến phản ánh tính chất, hay loại hình, không có biểu hiện trực tiếp bằng con số ví dụ giới tính, nghề nghiệp, tình trạng hôn nhân. Có hai dạng Nominal (định danh) ví dụ nghề nghiệp, và Ordinal (thứ bậc) ví dụ thứ hạng (Nhất, nhì,…)
Biến định lượng là biến biểu hiện trực tiếp bằng con số ví dụ tuổi, chiều cao, trọng lượng. Biến định lượng được chia làm 2 loại Discrete (biến định lượng rời rạc) ví dụ số học sinh 1 lớp và Continuous (biến định lượng liên tục) ví dụ nhiệt độ.
Biến nhị phân (binary variable) loại biến chỉ có 2 giá trị, 2 biểu hiện không trùng nhau của một đơn vị, nếu đơn vị không có giá trị này, thì phải chứa giá trị còn lại của biến thay phiên. Ví dụ có hoặc không, sống hoặc chết, rời dịch vụ hoặc còn tiếp tục sử dụng dịch vụ. Biến nhị phân có 2 dạng: Symmetric (đối xứng) và Asymmetric (không đối xứng)
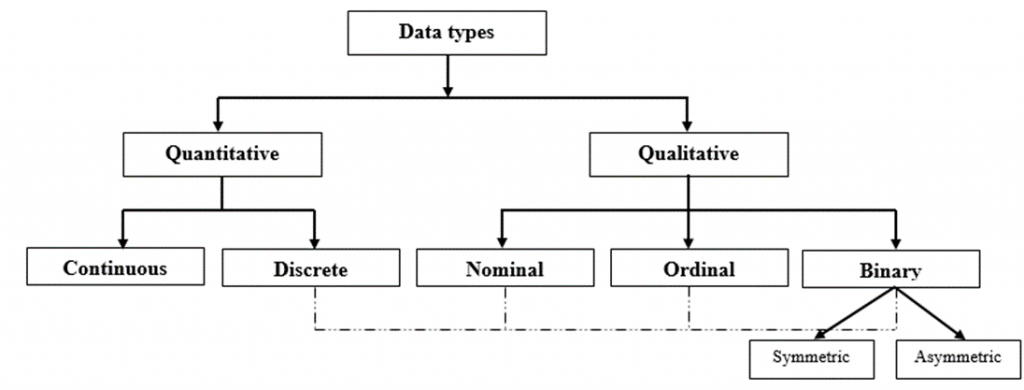
Lưu ý ở một số tài liệu khác có thể cho rằng biến rời rạc Discrete là biến định tính, lúc này các biến định danh, biến thứ bậc và biến thay phiên có thể thuộc biến rời rạc (do có thể các giá trị đếm được và khoảng giữa 2 giá trị không mang ý nghĩa).
Các loại biến hay loại dữ liệu của biến mục tiêu chính là cơ sở chọn lựa phương pháp hồi quy tương ứng.
- Với biến mục tiêu là biến định lượng liên tục thì phương pháp hồi quy đầu tiên mà chúng ta đã tìm hiểu qua chính là hồi quy tuyến tính – Linear regression gồm simple linear (tuyến tính đơn biến) và multiple linear (tuyến tính đa biến). Các phương pháp phân tích hồi quy chuyên sâu khác như Rigde regression (ngăn chặn vấn đề đa cộng tuyến và overfitting); Lasso regression (tăng độ chính xác của mô hình khi dự báo bằng cách đơn giản mô hình thông qua lựa chọn biến (variable selection process)); Partial least squares (PLS) regression, Principal component regression (PCA regression),…ngoài ra còn có các mô hình hồi quy phi tuyến khác.
- Với biến mục tiêu là biến định tính, hay biến thay phiên (hoặc biến rời rạc) thì phương pháp hồi quy chủ yếu, và thường là duy nhất chính là Logistic regression. Với biến định danh (Nominal) chúng ta có phương pháp Nominal Logistic regression, với biến thứ bậc (Ordinal) chúng ta có phương pháp Ordinal Logistic regression hay gọi tắt Ordinal regression, với biến thay phiên chúng ta có phương pháp Binary Logistic regression.
Logistic regression là gì? Mục đích ứng dụng?
Như vậy Logistic regression là phương pháp hồi quy thông dụng nhất, áp dụng cho các biến mục tiêu không phải là biến định lượng liên tục. Ở bài viết lần này và các bài viết sắp tới chúng tối sẽ chủ yếu trình bày chi tiết về Logistic regression áp dụng cho biến thay phiên hay còn gọi là Binary logistic regression, vì đây là dạng phổ biến nhất trong hồi quy logistic, là dạng đầu tiên, và được giảng dạy hầu hết trong các bộ môn liên quan đến thống kê. Các dạng còn lại Ordinal và Nominal, chúng tôi sẽ chỉ giới thiệu sơ trong một bài viết khác và gửi đến các bạn.
Sự khác biệt của biến mục tiêu chính là cơ sở phân biệt Logistic regression với các phương pháp hồi quy khác điển hình như Linear regression nên các bạn vui lòng lưu ý lại điểm này. Ngoài ra, chính sự khác biệt của biến mục tiêu nên cách thức lập phương trình, dạng phương trình, các giả định xung quanh đều sẽ khác nhau giữa 2 dạng hồi quy này. Tuy nhiên vẫn có điểm chung ở tất cả các phương pháp đó chính là mục tiêu phân tích.
Trước khi bắt đầu một nghiên cứu chi tiết về mô hình hồi quy logistic, điều quan trọng là phải hiểu rằng mục tiêu sử dụng mô hình này cũng giống như bất kỳ mô hình hồi quy nào khác trong thống kê, đó là, tìm ra mô hình phù hợp nhất và tối ưu nhất để mô tả mối quan hệ giữa biến mục tiêu y và một tập hợp các biến độc lập x (biến dự đoán hoặc giải thích) qua đó đưa ra các kết quả dự báo hay phân loại trong tương lai.
Ví dụ một ngân hàng muốn xây dựng một mô hình hồi quy dùng để ước lượng hay dự báo được hay không được cấp phát thẻ tín dụng cho một khách hàng bất kỳ. Biến mục tiêu y là biến thay phiên chỉ mang 2 giá trị. Giá trị y = 0 nghĩa là không được cấp phát thẻ tín dụng, và giá trị y = 1 nghĩa là được cấp phát thẻ tín dụng. Với một tập hợp các biến độc lập x ví dụ như tuổi, nghề nghiệp, thu nhập, tài sản,…, ngân hàng có thể sử dụng Logistic regression để dự báo khả năng hay xác suất cấp phát thẻ tín dụng cho một khách hàng bất kỳ.
Một ví dụ khác của logistic regression trong việc dự báo khả năng xảy ra của một sự kiện, tình huống trong tương lai. Ví dụ một công ty muốn biết khả năng khách hàng truy cập website và chọn các ưu đãi trên đó – hoặc không chọn (đây là 2 giá trị của biến mục tiêu). Các đặc điểm đã biết của khách hàng truy cập, chẳng hạn như các website khác họ đã truy cập trước khi vào website công ty, tần suất truy cập lại vào website công ty, hành vi trên website công ty (đây là các biến độc lập x). Các mô hình hồi quy logistic lúc này được sử dụng để xác định xác suất loại khách truy cập nào có khả năng chấp nhận chọn ưu đãi – hay không chọn ưu đãi. Do đó, công ty sẽ có thể đưa ra quyết định tốt hơn về chiến dịch quảng cáo ưu đãi của mình hoặc đưa ra chính sách tốt hơn về chính ưu đãi đó.
Điểm khác biệt thứ 2 giữa logistic regression và hồi quy tuyến tính, chính là kết quả của biến mục tiêu y trong hồi quy tuyến tính (hay các dạng hồi quy áp dụng cho biến mục tiêu là biến định lượng liên tục) là giá trị số (numerical value) còn kết quả dự báo của biến mục tiêu y trong logistic regression sẽ mang giá trị xác suất (probability) để phân loại đối tượng nghiên cứu hay quyết định giá trị cuối cùng của biến y trong danh mục các giá trị định tính.
Qua đó chúng ta thấy được điểm khác biệt thứ 3 là đối với các dạng hồi quy áp dụng cho biến mục tiêu là biến định lượng thì nhiệm vụ phân tích sau cùng sẽ là đưa ra kết quả dự báo chính xác (value prediction) còn hồi quy logistic sau cùng có cả kết quả phân loại chính xác (category classification). Ví dụ sau khi tính toán, phân loại được khách hàng A sẽ được cấp phát thẻ tín dụng khi giá trị y được dự báo = 1.
Các bạn còn nhớ ở đầu bài viết chúng tôi có nói “…phổ biến không chỉ trong lĩnh vực thống kê mà còn ở lĩnh vực khai phá dữ liệu – Data mining.”. Nguyên nhân là logistic regression có khả năng phân loại đối tượng nghiên cứu dựa trên các yếu tố đầu vào, tức góp phần thực hiện một trong các task quan trọng nhất trong Data mining đó là Classification. Cũng vì thế mà logistic regression ngày nay có khi được ứng dụng phổ biến hơn cả linear regression.
Để biết Classification là gì trong Data mining, bạn nào chưa biết có thể tham khảo bài viết sau của chúng tôi:
Tổng quan về Data mining (P.3): quá trình và phương pháp
Thuật toán KNN và ví dụ đơn giản trong ngành ngân hàng
Theo IBM, Logistic regression hay logit model được ứng dụng trong phân tích dự báo, đã được ứng dụng rộng hơn trong lĩnh vực học máy – Machine learning. Logistic regression xuất hiện trong các phần mềm thống kê và khai phá dữ liệu, giúp người dùng tìm hiểu mối quan hệ giữa biến mục tiêu là biến định tính và một hay nhiều biến độc lập thông qua thiết lập phương trình hồi quy logit.
Ứng dụng logistic regression trong việc xây dựng mô hình dự báo đối với các công ty ngày nay như là một phương pháp tạo nên sự khác biệt và lợi thế cạnh tranh. Vì đơn giản các mô hình dự báo sẽ giúp họ khai phá các mối quan hệ, những yếu tố sẽ tác động lên doanh thu, lợi nhuận trong tương lai, thông qua tìm hiểu hành vi của khách hàng, từ đó ra quyết định, chiến lược hiệu quả hơn. Một nhóm phân tích dữ liệu của một nhà máy sản xuất có thể sử dụng logistic regression để dự báo khả năng hư hỏng của các thành phần máy móc thiết bị dựa trên khoảng thời gian chúng được lưu trữ trong kho. Với kết quả có được từ quá trình phân tích, nhà máy có thể đưa ra kế hoạch bảo dưỡng, lắp đặt hợp lý. Còn rất nhiều ứng dụng khác của logistic regression trong kinh doanh khác mà điển hình như công ty có thể sử dụng để dự báo khả năng khách hàng rời dịch vụ, phân khúc khách hàng theo nhóm sản phẩm mục tiêu dựa trên đặc điểm mua hàng, thông tin cá nhân.Trong lĩnh vực y tế logistic regression có thể được sử dụng để dự đoán khả năng mắc bệnh của một nhóm dân số nhất định để áp dụng các biện pháp phòng ngừa.
Trong lĩnh vực ngân hàng, logistic regression được dùng để đánh giá rủi ro tín dụng. Hãy tưởng tượng rằng bạn là nhân viên cho vay tại ngân hàng và bạn muốn xác định các đặc điểm của những người có khả năng nợ xấu (không thể thanh toán nợ) sau khi vay. Sau đó, bạn muốn sử dụng những đặc điểm đó để xác định rủi ro tín dụng là tốt và xấu cho từng khách hàng. Bạn có dữ liệu trên 1000 khách hàng trong đó 800 khách hàng đã nhận được khoản vay. Lúc này logistic regression là phương pháp hữu hiệu nhất. Bạn có thể sử dụng một mẫu ngẫu nhiên trong số 800 khách hàng này để tạo mô hình hồi quy logistic và phân loại 200 khách hàng còn lại có nguy cơ nợ xấu hay không, trên cơ sở trong 800 khách hàng ấy có người đã thanh toán toàn bộ khoản vay, và người chưa thể thanh toán. Ngoài ra trong lĩnh vực ngân hàng, bên cạnh ngăn chặn rủi ro, logistic regression có thể giúp gia tăng lợi nhuận bằng cách giúp ngân hàng tiếp cận đúng khách hàng đúng sản phẩm, dịch vụ.
Tóm lại vậy khi nào là thích hợp nhất để áp dụng hồi quy logistic vào quy trình phân tích dữ liệu? Thứ nhất, khi chúng ta cần phân loại đối tượng nghiên cứu vào các nhóm, các loại và tên các nhóm, các loại nằm trong dãy giá trị của biến mục tiêu ví dụ phân loại khách hàng mục tiêu vào nhóm A, B, C, D, giá trị sau cùng của biến mục tiêu y = {A, B, C, D} (dạng nomial, ordinal logistic regression). Thứ hai, khi chúng ta dự báo một sự kiện xảy ra trong tương lai chỉ với 2 khả năng có hoặc không, biến mục tiêu y sẽ chỉ có 2 giá trị 0 = không, 1 = có (dạng binary logistic regression – thông dụng nhất.)
Phương trình tổng quát của Logistic regression (binary)
Nếu bạn nào chưa tiếp cận các kiến thức về hồi quy mà khởi đầu là hồi quy tuyến tính thì có lẽ khi nhìn vào công thức tổng quát của hồi quy logistic chúng tôi sắp nói sau đây sẽ cảm thấy phức tạp. Nhưng thực chất phương trình hồi quy logistic cũng giống như phương trình hồi quy đơn giản thông thường như ở các dạng khác cụ thể:
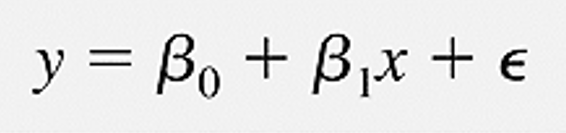
Tuy nhiên như đã nói, kết quả của phương trình hồi quy logistic là xác suất và dựa vào xác suất để quyết định giá trị sau cùng của biến y. Đối với hồi quy logistic, biến y chỉ có 2 giá trị ví dụ như có và không, thành công và thất bại, sống sót và chết, còn sử dụng dịch vụ và không còn sử dụng dịch vụ thông thường theo thông lệ các chuyên gia phân tích sẽ gán y = 0 cho các kết quả “không”, “thất bại”, “chết”, “rời dịch vụ”, còn gán y = 1 cho giá trị còn lại. Nói chung là y = 1 thường hướng đến kết quả tích cực, kết quả mong đợi của người phân tích. Các bạn vẫn có thể đặt ngược lại, điều này không sao, nhưng nhớ note lại để tránh bị nhầm lẫn.
Như vậy chính xác hơn, phương trình tổng quát của hồi quy logistic regression sẽ có dạng tổng quát với p là xác suất cần tìm.
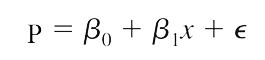
Xác suất chỉ có giá trị từ 0 đến 1, trong bài viết này chúng tôi quy định khi xác suất có giá trị lớn tiến đến 1 thì tương ứng khả năng y = 1 càng cao, và khi xác suất có giá trị tiến đến 0 thì tương ứng khả năng y = 0 càng cao. Lưu ý giá trị 0 và 1 của y không phải giá trị số thực, mà là kết quả mã hóa (coding) của những giá trị định tính của biến y, ví dụ y = 0 nghĩa là đối tượng nghiên cứu trong tương lai có thể “không mua hàng”, “đã rời dịch vụ”, “nợ xấu”, y = 1 thì suy ngược lại.
Với p là biến phụ thuộc, xác suất khả năng y xảy ra 0 hoặc 1 (chịu ảnh hưởng của biến x), là biến chúng ta sẽ dự báo giá trị, x là biến độc lập (biến tác động lên biến phụ thuộc), β0 là giá trị ước lượng của p khi x đạt giá trị 0, β1 dùng để xác định giá trị trung bình của p tăng hay giảm khi x tăng, ε là sai số, thể hiện giá trị của các yếu tố khác không thể nghiên cứu hết và các yếu tố này vẫn tác động lên giá trị p.
Tuy nhiên phương trình tổng quát trên lại không thích hợp trong việc ước lượng xác suất trung bình của biến mục tiêu y cho một đối tượng bất kỳ trong tổng thể nghiên cứu mặc dù chúng vẫn thể hiện mối quan hệ giữa biến y và biến x bằng hệ số hồi quy β.
Như đã nói nếu sử dụng phương trình trên thì giá trị xác suất p có thể không nằm trong giới hạn 0 và 1, tức có thể p lớn hơn 1 hoặc p bé hơn 0 mang giá trị âm. Với phương trình trên chúng ta có:
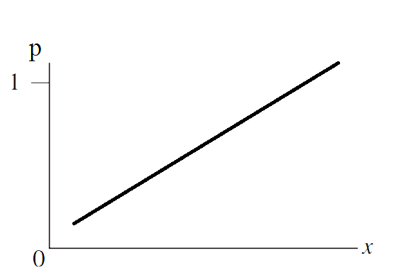
Đồ thị giống hồi quy tuyến tính, không thích hợp để miêu tả kết quả phân tích hồi quy logistic. Các chuyên gia cho rằng cần xây dựng một phương trình hồi quy với đồ thị giới hạn được xác suất p từ 0 đến 1. Cụ thể như sau:
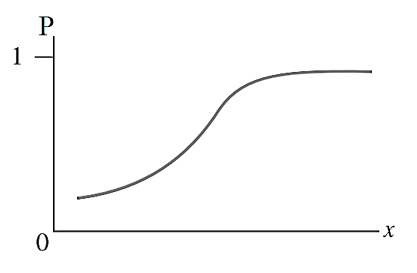
Phương trình tổng quát của đồ thị dạng đơn biến:
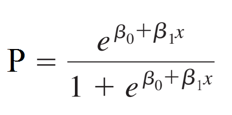
Công thức thể hiện dưới dạng phân số với mẫu số luôn lớn hơn tử số do đó giới hạn giá trị của p nằm giữa 0 và 1. Với đồ thị dạng hình cong chữ S, xác suất p sẽ luôn nằm trong khoảng 0 với 1 tại bất kỳ giá trị nào của x. Ở bài viết tới chúng ta sẽ tìm hiểu kỹ hơn tại sao lại có phương trình trên, còn trong bài viết này chúng tôi sẽ không đề cập chi tiết khi trình bày công thức xác định các hệ số hồi quy β.
Tham số β trong mô hình thể hiện giá trị trung bình của p tăng hay giảm khi x tăng. Khi β1 > 0, xác suất p tăng khi x tăng. Khi β1 < 0, xác suất p giảm khi x tăng. Nếu β1 = 0, p không thay đổi khi x thay đổi, lúc này đường cong sẽ biến thành một đường thẳng nằm ngang. Độ dốc của đường cong tăng khi giá trị tuyệt đối của β1 tăng. Tuy nhiên, không giống như trong đồ thị đường thẳng trong hồi quy tuyến tính, β1 không phải là độ dốc và do đó không thể được hiểu là sự thay đổi về giá trị trung bình p khi x thay đổi 1 đơn vị. Đối với đường cong hình chữ S này, tỷ lệ đường cong dốc lên hoặc thoải, thay đổi như thế nào dựa trên phạm vi của các giá trị x. Các bạn hãy xem qua đồ thị dưới đây để hiểu rõ hơn.
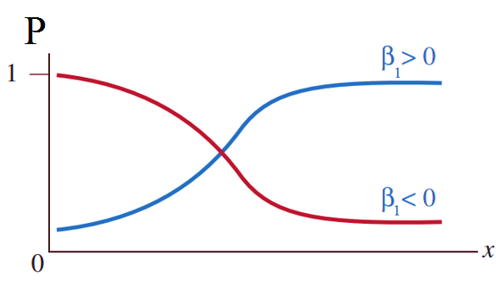
Bên trên là phương trình tổng quát hồi quy logistic đơn biến với duy nhất 1 biến độc lập và một biến mục tiêu y nên có 1 hệ số β1. Trong thực tế khi phân tích chúng ta sẽ quan tâm nhiều hơn đến tất cả các yếu tố liên quan đến đối tượng mục tiêu nghiên cứu hay còn gọi là biến y.
Ngoài ra mục tiêu là dự báo hay ước lượng xác suất trung bình dẫn đến khả năng y = 1 hay y = 0 dựa trên phương trình tìm được. Vì vậy phương trình tổng quát tiêu chuẩn dạng đa biến là:
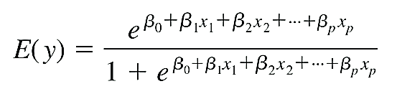
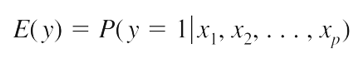
Phương trình tổng quát để ước lượng xác suất dạng đa biến:
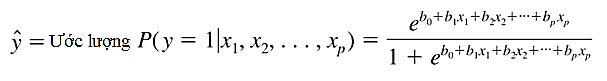
Ví dụ đơn giản đầu tiên để hiểu sơ về hồi quy logistic, trước tiên là hồi quy logistic đơn biến. Giả sử một đại lý du lịch tại thành phố Hồ Chí Minh có dữ liệu lịch sử về 100 khách hàng đăng ký tour du lịch trong tuần vừa qua, trong đó có các khách hàng đăng ký tour hạng sang. Không xét nghề nghiệp, đại lý chỉ muốn tìm hiểu thu nhập có tác động thế nào đến việc khách hàng chọn tour du lịch hạng sang hay không. Lấy mẫu 20 khách hàng để xây dựng mô hình hồi quy logistic.
Với x là biến thu nhập hàng tháng, y là thông tin khách hàng có hay không đăng ký tour hạng sang, y = 1 là có, y = 0 là không. Chúng ta có bộ dữ liệu mẫu 20 khách hàng sau:
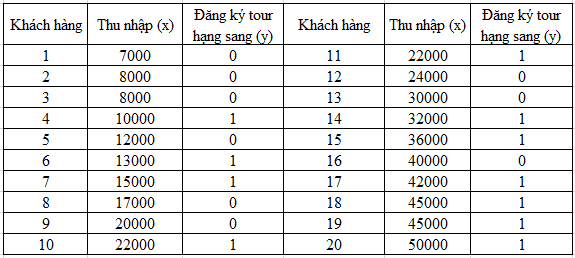
Chúng ta sẽ sử dụng phần mềm thống kê để tìm phương trình hồi quy logistic, ở đây chúng tôi sử dụng SPSS Statistics. Lưu ý thu nhập đơn vị 1000 VND.
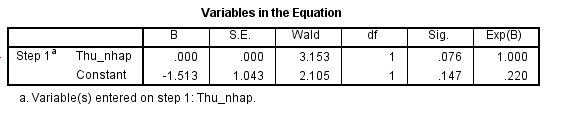
Hệ số β1 của biến thu nhập là 0.000072, β0 là -1.513. Lưu ý do chênh lệch giữa thu nhập và giá trị coding cho biến đăng ký ví dụ giữa 22000 và 1 thì 22000 là số quá lớn so với 1, nên khi tính toán kết quả hệ số β1 sẽ rất nhỏ, nếu các bạn thử chia 1000 và lấy đơn vị là triệu VND như 22 là 22 triệu thì hệ số sẽ là 0.72 không còn quá nhỏ.
Kết quả phương trình hồi quy logistic đơn biến có được là:
P = (e-1.513 + 7.2*10^(-5)*x) / (1 + e-1.513 + 7.2*10^(-5)*x)
Hệ số β1 mang giá trị dương nên khi giá trị x tăng thì xác suất p tăng tức là thu nhập tăng thì khả năng khách hàng đăng ký tour hạng sang cũng tăng.
Giả sử thu nhập khách hàng thứ 101 là 18 triệu VND/ 1 tháng, xác suất ước lượng thể hiện khả năng đăng ký tour hạng sang là 44%. Thu nhập khách hàng thứ 102 là 25 triệu VND/ 1 tháng, xác suất ước lượng thể hiện khả năng đăng ký tour hạng sang là 57%. Các bạn có thể thay trực tiếp vào công thức để tính.
Như vậy đến đây là kết thúc phần 1 bài viết, ở phần 2 chúng ta sẽ tìm hiểu sâu hơn về phương trình hồi quy logistic và cũng như các công thức quan trọng khác như đánh giá độ hiệu quả mô hình, tính chính xác trong dự báo, sử dụng ví dụ ứng dụng logistic regression trong tài chính hay bán lẻ để hiểu rõ hơn. Mong các bạn tiếp tục ủng hộ BigDataUni.
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English