Ở những bài viết trước về các thuật toán cây quyết định, Decision trees hay Classification & Regression trees, chúng tôi đã đề cập đến phương pháp phân tích hồi quy, Regression analysis, cụ thể trong phần cuối cùng về Regression tree, cách sử dụng cây quyết định để dự báo giá trị của biến mục tiêu (là biến định lượng), dựa trên các thuộc tính, đặc điểm nằm ở những biến đầu vào còn lại của các đối tượng dữ liệu. Mô hình cây quyết định sử dụng chính nguyên lý hoạt động của các phương trình hồi quy, đó là tìm ra mối quan hệ giữa những biến độc lập với biến phụ thuộc, giữa những biến đầu vào và biến dự báo, cũng vì vậy nên được gọi là Regression tree.
Tuy nhiên nếu nhìn vào các mô hình Regression tree, chúng ta chỉ thấy được sự tác động của biến này hay biến kia đến giá trị sau cùng của biến mục tiêu, nói cách khác, chỉ xác định được mối quan hệ nhân quả giữa các biến thông qua diễn giải Decision rules (hoặc nguyên lý nếu…thì) nhưng không thể nhìn thấy mức độ quan hệ, hay biến mục tiêu và các biến đầu vào quan hệ như thế nào về mặt định lượng, qua đó để dự báo giá trị của biến mục tiêu. Chúng ta cùng xem qua ví dụ dưới đây:
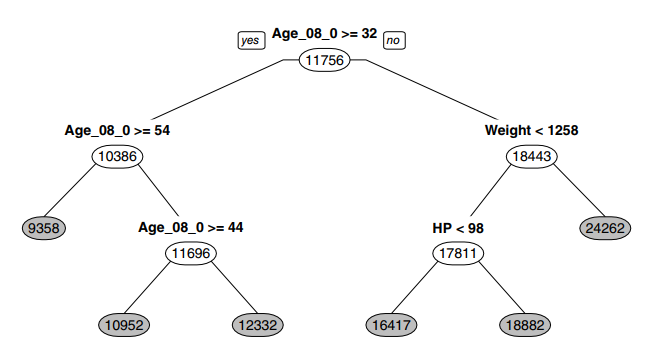
Ví dụ được lấy từ tài liệu “Data mining for business analytics – concepts, techniques and applications in R” của tác giả Galit Shmueli và các cộng sự. Bên trên là mô hinh Regression tree dự báo giá của một chiếc xe Toyota dựa trên 3 biến: tuổi đời chiếc xe (Age), trọng lượng (Weight) và mã lực (Horse power – HP), đã được chọn lọc trong 12 biến có được trong tập dữ liệu về 1000 chiếc xe Toyota Corolla, được lấy ra 600 để làm tập dữ liệu training. Ví dụ với chiếc xe có độ tuổi là 55, mã lực bằng 100 thì có thể bán với giá 9358$.
Các bạn có thể thấy mối quan hệ giữa độ tuổi với giá trị của chiếc xe, tức độ tuổi cao hay thấp sẽ có tác động nhất định với giá trị của chiếc xe, tương tự như mã lực cao hay thấp, tuy nhiên tác động của độ tuổi, và mã lực đến giá xe, tác động nào mạnh hơn, lớn hơn? Dựa trên mô hình cây quyết định chúng ta khó có thể xác định được. Cũng chính vì thế, để diễn giải kết quả phân tích hồi quy, hoặc mô tả mối quan hệ theo cách định lượng hóa, thì mô hình cây quyết định thường không được phổ biến hay ưu tiên áp dụng, mà thay vào đó là sử dụng những phương trình hay mô hình hồi quy bao gồm các công thức định lượng mối quan hệ giữa các biến, các phương pháp kiểm định để chắc chắn các biến có mối liên hệ, và kết hợp với những đồ thị trực quan.
Trong chủ đề bài viết về phương pháp hồi quy, Regression, ở phần 1, chúng ta sẽ làm quen với khái niệm Regression là gì, tổng quan về các dạng phân tích hồi quy và giới thiệu một chút về phương pháp phân tích sự tương quan (Correlation) – phương pháp xác định liệu các biến có mối liên hệ tuyến tính với nhau hay không, chiều hướng và mức độ quan hệ giữa các biến như thế nào.
Phần 2 bài viết, chúng ta sẽ tìm hiểu về cách thức xác định mối quan hệ giữa 2 biến đơn giản bất kỳ, sử dụng Correlation và Regression (dạng đầu tiên Simple linear regression).
Correlation và Regression là gì?
Có lẽ sẽ có bạn thắc mắc tại sao trọng tâm bài viết là về Regression nhưng chúng tôi lại đề cập về phương pháp phân tích sự tương quan, Correlation, đầu tiên. Đơn giản, chúng ta có thể xác định biến mục tiêu và biến độc lập có quan hệ với nhau hay không và quan hệ như thế nào về mặt định lượng chỉ bằng phương pháp hồi quy. Tuy nhiên trong những trường hợp chúng ta muốn tìm hiểu nhanh liệu 2 biến bất kỳ có quan hệ với nhau, mức độ quan hệ ra sao hay không mà chưa cần dùng đến phương pháp hồi quy phức tạp hay muốn kiểm chứng từ phương trình hồi quy lần nữa xem 2 biến có quan hệ với nhau không, thì phương pháp phân tích tương quan sẽ cho chúng ta kết quả nhanh chóng. Qua các giải thích trên chắc các bạn đã phần nào hiểu được phân tích tương quan là gì.
Correlation là phương pháp nghiên cứu mối quan hệ tuyến tính giữa 2 hay nhiều biến khác nhau, dựa trên đo lường mức độ quan hệ, hay cường độ quan hệ tuyến tính.
Điểm khác biệt thứ nhất giữa tương quan và hồi quy mà chúng tôi trình bày trong bài viết này, đó là Correlation không quan tâm biến nào sẽ là biến độc lập và biến nào sẽ là biến phục thuộc, các biến ở vị thế “ngang nhau”, tức biến này có thể tác động lên biến kia và ngược lại, còn Regression chỉ quan tâm đến biến mục tiêu, tìm hiểu xem các biến khác sẽ tác động ra sao lên biến mục tiêu này.
Correlation sử dụng hệ số tương quan (Correlation Coefficient) và phương pháp kiểm định hệ số tương quan để xem xét giữa các biến có mối quan hệ tương quan hay nhau. Lưu ý lần nữa, tương quan theo nghĩa tiếng Việt đơn giản là tác động qua lại giữa hai phía, nghĩa là phương pháp này có thể xem xét mối liên hệ theo 2 chiều, còn Regression thì thể hiện khía cạnh 1 chiều (biến độc lập tác động thế nào đến biến mục tiêu chứ không xét ngược lại).
Regression là phương pháp nghiên cứu mối quan hệ giữa 2 biến mà cụ thể một biến sẽ là biến độc lập (ảnh hưởng đến biến mục tiêu), và biến còn lại sẽ là biến mục tiêu (bị ảnh hưởng bởi biến độc lập), mô hình hóa, định lượng hóa mối quan hệ này để qua đó có thể xác định được giá trị của biến mục tiêu nếu các biến độc lập thay đổi như thế nào.
Điểm khác biệt thứ hai, có thể là khác biệt lớn nhất đó chính là kết quả của phân tích hồi quy, chính là kết quả dự báo của biến mục tiêu. Đây là cơ sở để Regression còn là phương pháp chính trong Predictive analytics (phân tích dự báo) bên cạnh là kiến thức nền tảng trong lĩnh vực thống kê (Statistics) và khai phá dữ liệu (Data mining). Còn kết quả của Correlation chỉ dừng lại ở việc đánh giá có mối quan hệ giữa 2 biến hay không, đo lường chiều hướng và tính bền vững trong mối quan hệ này. Cụ thể hệ số tương quan của Correlation sẽ nằm từ -1 đến 1:
- Nếu hệ số < 0, thì 2 biến có mối quan hệ theo chiều nghịch nhau, tức một biến tăng thì biến còn lại sẽ giảm hoặc ngược lại.
- Hệ số > 0 thì 2 biến có mối quan hệ thuận, một biến tăng, biến còn lại có thể tăng theo hoặc ngược lại.
- Hệ số = 0, 2 biến không có mối quan hệ tuyến tính với nhau.
- Hệ số càng tiến gần giá trị -1, mối liên hệ nghịch càng chắc chắn, tương tự với giá trị 1, mối liên hệ thuận càng chắc chắn.
Giải thích một chút về từ quan hệ tuyến tính (linear relationship), như các bạn đã từng được học ở các lớp phổ thông hay trung học về đồ thị hàm số, cho các giá trị của x và các giá trị y tương ứng, nhiệm vụ là tìm phương trình và vẽ đồ thị. Nếu phương trình mà các bạn lập được thành công, và đồ thị các bạn vẽ được là một đường thẳng thì lúc này các bạn đã chứng minh giữa x và y đã có mối quan hệ tuyến tính (chưa xét đến nghịch hay thuận).
Nhưng đó chỉ là bài toán rất đơn giản để chúng ta hiểu thế nào là mối quan hệ tuyến tính giữa x và y. Trong thực tế, khi tìm hiểu về mối quan hệ giữa 2 hay nhiều đối tượng, hiện tượng nghiên cứu khác nhau ở mọi lĩnh vực và đảm bảo kết quả chính xác thì dữ liệu cần phân tích là rất nhiều, do đó các công thức tính toán như trước đây chúng ta từng được học sẽ không thể nào áp dụng. Lúc này phương pháp Correlation và Regression sẽ cực kỳ hữu dụng. Giả sử chúng ta có một tập dữ liệu gồm nhiều giá trị x, và tương ứng với mỗi giá trị x là một giá trị, chúng ta sẽ có các điểm dữ liệu gọi là Mi (xi, yi), nếu các điểm dữ liệu này nằm trên cùng một đường thẳng chứng tỏ x và y có quan hệ tuyến tính và ngược lại.

Giá trị x tăng thì y tăng theo, lúc này x và y có quan hệ tuyến tính thuận, hệ số tương quan sẽ lớn hơn 0 nhưng chưa chắc tiến gần 1, chưa có cơ sở khẳng định mối quan hệ này vững chắc.

Hình trên thì x và y không thể hiện mối quan hệ tuyến tính, lúc này hệ số tượng quan có thể gần giá trị 0.

Giá trị x giảm, giá trị y lại tăng, x và y thể hiện mối quan hệ tuyến tính nghịch, lúc này hệ số tương quan sẽ mang giá trị âm và nhỏ hơn 0, nhưng chưa chắn tiến gần giá trị -1 và không có cơ sở khẳng định mối quan hệ này là bền vững.

Giá trị x tăng, y chắc chắn sẽ tăng, lúc này x và y thể hiện mối quan hệ tuyến tính thuận và cực kỳ bền vững và hoàn hảo, lúc này giá trị của hệ số tương quan có thể bằng 1.

Giá trị của x giảm, và y chắc chắn tăng, lúc này giữa x và y thể hiện mối quan hệ tuyến tính nghịch, và mối quan hệ này bền vững, giá trị của hệ số tương quan sẽ bằng -1. Công thức của hệ số tương quan tổng quát như sau:

Với Sxy là hiệp phương sai (Covariance) của x và y, Sx là độ lệch chuẩn của các giá trị x, Sy là độ lệch chuẩn của các giá trị y. Hiệp phương sai của x và y cũng là một chỉ số thể hiện sự tương quan của 2 biến bất kỳ. Bên cạnh việc tính toán hệ số tương quan, chúng ta còn có thể sử dụng phương pháp kiểm định giả thuyết t để củng cố kết luận của mình. Lưu ý công thức ở trên áp dụng cho xác định mối quan hệ giữa x và y cho bộ dữ liệu mẫu (Sample) không phải dữ liệu tổng thể.
Ở bài viết sắp tới về cách phân tích mối quan hệ giữa 2 biến bất kỳ, chúng tôi sẽ trình bày lại Correlation trong ví dụ cụ thể, tương tự như dạng đầu tiên của Regression là Simple linear regression. Còn ở phần 1 kỳ này chúng tôi chỉ dừng lại ở phần giới thiệu mà thôi.
Correlation và Regression là 2 phương pháp thường song hành nhau trong lĩnh vực thống kê. Ví dụ như nếu chỉ sử dụng Correlation, và nhìn vào biểu đồ hay giá trị của hệ số tương quan chúng ta sẽ thấy được mối quan hệ tuyến tính giữa x và y chỉ trong dữ liệu lịch sử, vậy muốn lập phương trình, muốn đưa ra dự báo về giá trị y khi trong tương lai giá trị x thay đổi một lượng bất kỳ, thì chúng ta phải sử dụng phương pháp Regression. Đối với dạng tuyến tính cho 2 biến, thì chúng ta có phương trình hồi quy tổng quát, và đơn giản nhất của Regression như sau:
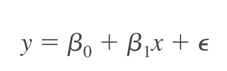
Với y là biến phụ thuộc (chịu ảnh hưởng của biến x), là biến chúng ta sẽ dự báo giá trị, x là biến độc lập (biến tác động lên biến phụ thuộc), β0 là giá trị ước lượng của y khi x đạt giá trị 0, β1 là độ dốc của đường hồi quy tuyến tính, nói cách khác là mức độ thay đổi của y khi x thay đổi 1 đơn vị, ε là sai số, thể hiện giá trị của các yếu tố khác không thể nghiên cứu hết và các yếu tố này vẫn tác động lên giá trị của y.
Cách xác định các tham số sẽ được chúng tôi trình bày ở bài viết sắp tới. Tuy nhiên trong thực tế chúng ta không chỉ có nghiên cứu mối quan hệ giữa 2 biến độc lập và biến phụ thuộc, mà còn nghiên cứu mối quan hệ của nhiều biến độc lập và biến phụ thuộc, và không chỉ có mối quan hệ tuyến tính mà còn nhiều mối quan hệ phức tạp hơn giữa các biến mà chúng ta phải khai phá. Chính vì thế chúng ta có nhiều phương trình hồi quy và nhiều đồ thị trực quan thể hiện các phương trình từ đơn giản đến phức tạp khác nhau. Do đó mặc dù là kiến thức nền tảng và xuất hiện đầu tiên trong lĩnh vực thống kê (Statistics) nhưng Regression với nhiều dạng khác nhau, được ứng dụng nhiều trong các lĩnh vực khác nhau không chỉ riêng ở lĩnh vực khoa học dữ liệu.
Các dạng, các loại mô hình (phương trình) hồi quy phổ biến
Các mô hình hồi quy có thể được phân loại theo nhiều cách như các mô hình tuyến tính (linear) và phi tuyến tính (non-linear); các mô hình áp dụng cho biến định lượng và các mô hình áp dụng cho biến định tính; các mô hình áp dụng cho phân tích mối quan hệ giữa 2 biến hay nhiều hơn 2 biến; các mô hình có tham số và không có tham số; các mô hình cổ điển và hiện đại (những mô hình mở rộng).
Các bạn có thể tham khảo thêm về cách thức phân loại các mô hình hồi quy ở những tài liệu khác, và do có rất nhiều dạng mô hình hồi quy khác nhau nên trong bài viết này chúng tôi sẽ chỉ giới thiệu một số mô hình hồi quy nhất định mà thôi và chi tiết về cách thức thực hiện sẽ được chúng tôi trình bày ở các phần tiếp theo.
- Linear Regression
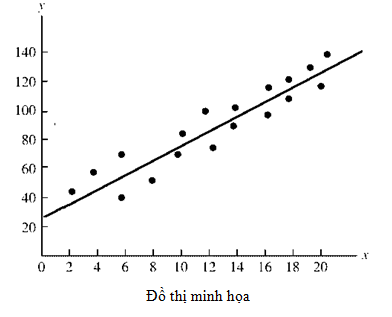
Simple linear regression, đây được xem là mô hình hồi quy đơn bội, đơn giản nhất và phổ biến nhất, chỉ nghiên cứu mối quan hệ tuyến tính giữa một biến độc lập và biến phụ thuộc, áp dụng cho biến định lượng, và đồ thị là dạng đường thẳng Phương trình tổng quát:
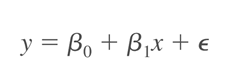
Đồ thị minh họa
Multiple regression (Multi linear regression), mô hình hồi quy đa bội áp dụng cho nghiên cứu mối quan hệ của nhiều biến độc lập và một biến phụ thuộc, áp dụng cho biến định lượng. Phương trình tổng quát:
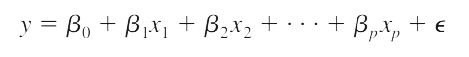
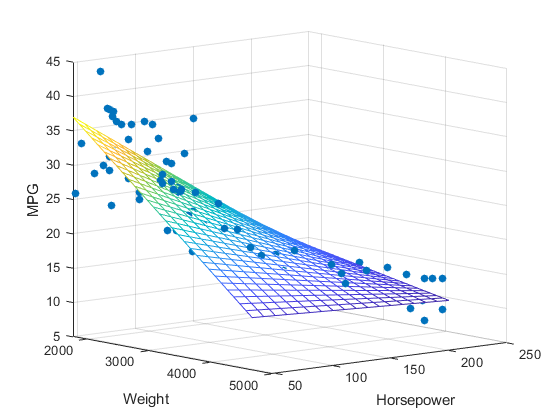
Đồ thị minh họa (nguồn hình Analyticsvidhya post – Medium)
- Logistic Regression
Mô hình hồi quy Logit áp dụng cho biến phụ thuộc là biến định đính hoặc định lượng chỉ có 2 giá trị, hay còn gọi là biến thay phiên (Binary) ví dụ y chỉ có 2 giá trị là 0 và 1, có hoặc không,… Phương trình tổng quát: Logistic Regression cho đơn biến
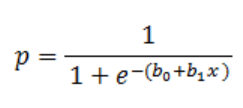
Logistic Regression cho mô hình đa biến
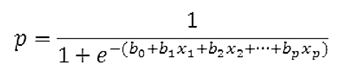
Với p là xác suất xảy ra giá trị y = 1 hay y = “có”,… Đồ thị minh họa dưới đây, lưu ý đồ thị hình cong không theo đường thẳng, nên logistic regression không phải dạng hồi quy tuyến tính
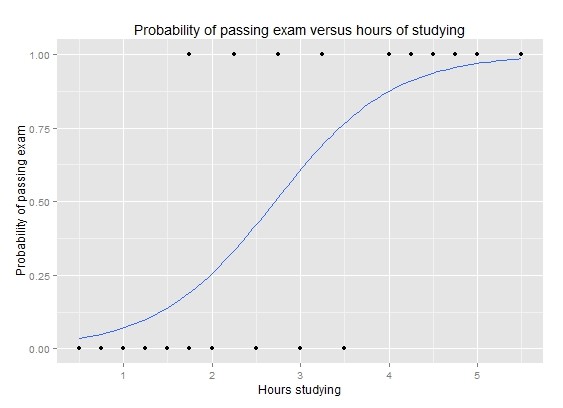
(Nguồn hình: En.wikipedia)
- Polynominal Regression
Mô hình hồi quy Polynominal áp dụng cho các trường hợp mà biến độc lập x có bậc mũ lớn hơn 1, và y là biến định lượng. Phương trình tổng quát:
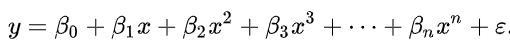
Đồ thị của mô hình hồi quy này không phải đường thẳng, và là một đường cong, do đó đây không phải dạng hồi quy tuyến tính. Đồ thị minh họa:
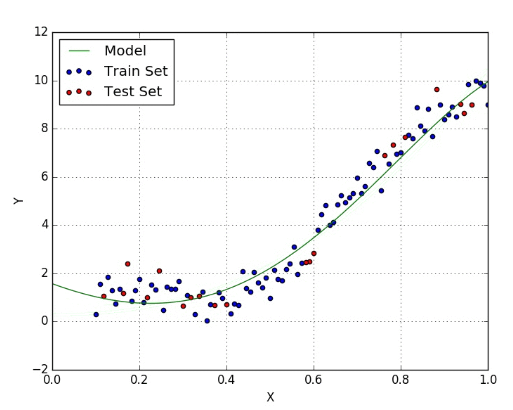
(Nguồn hình towardsdatascience )
- Quantile Regression
Là dạng mô hình hồi quy mở rộng của hồi quy tuyến tính – Linear regression, tìm hiểu mối quan hệ tuyến tuyến giữa biến độc lập và biến phụ thuộc trong trường hợp bộ dữ liệu có các giá trị ngoại lệ (outliers), độ lệch/ chệch cao của phân phối dữ liệu (high skewness), mức độ không đồng nhất của dữ liệu. Mô hình dựa trên xem xét phân phối tổng thể của dữ liệu, không chỉ sử dụng mỗi giá trị trung bình để tính toán, xây dựng công thức như trong linear regression.
Quantile chính là phân vị trong lĩnh vực thống kê, là phương pháp xác định với n % bất kỳ của bộ dữ liệu thì phân phối các giá trị của dữ liệu trong n % là như thế nào (các giá trị đãđược sắp xếp từ nhỏ đến lớn) để đánh giá độ phân tán của dữ liệu, và tại phân vị thứ n này giá trị đạt được của biến là bao nhiêu. Phương trình tổng quát của Quantile Regression tương tự như Linear regression, và y biến định lượng liên tục (Continuous varibale), tuy nhiên Quantile Regression hướng đến giảm thiểu sai số của mô hình với công thức tổng quát như sau: Phương trình tổng quát:
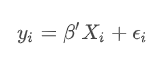
Công thức tính sai số có trọng số theo mô hình hồi quy

Với τ là phân vị cần xét của tập dữ liệu. Đồ thị minh họa:
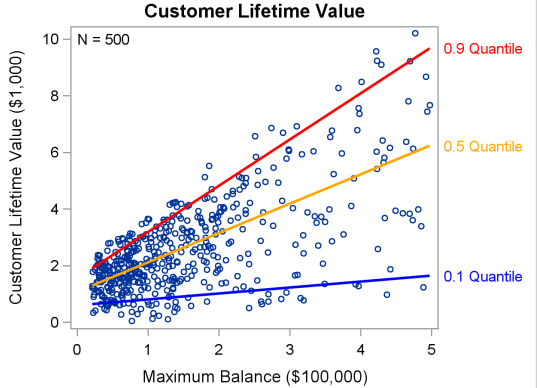
- Ridge Regression (Shrinkage regression)
Mô hình Ridge Regression là phương pháp áp dụng khi bộ dữ liệu gặp vấn đề về đa cộng tuyến (các biến độc lập x có mối liên hệ với nhau, và ảnh hưởng lên kết quả dự báo của y), hay giải quyết các vấn đề về Overfitting (mô hình áp dụng tốt cho dữ liệu training nhưng không không hoạt động tốt trên dữ liệu test) mà mô hình hồi quy tuyến tính thông thường gặp phải. Phương trình tổng quát của linear regression cho đơn biến và đa biến các bạn có thể để ý sẽ thấy giá trị ε ở đằng sau mỗi phương trình.
Đậy là sai số của các phương trình hồi quy, là chênh lệch giữa kết quả dự báo và kết quả thực tế. Các sai số được chia thành 2 phần: Biased (thiên vị), Variance (phương sai). Biased là trường hợp mô hình phân tích không khớp, không đem lại kết quả chính xác trên tập dữ liệu training, còn Variance là đối với dữ liệu test. Mối quan hệ đánh đổi giữa Biased và Variance xét trên mức độ phức tạp của mô hình, chúng tôi sẽ đề cập vấn đề này trong chính bài viết về Ridge regression sắp tới.

Nguồn hình francescopochetti.com
Ridge Regression là mô hình hồi quy phân tích mối quan hệ giữa các biến độc lập và biến phụ thuộc sử dụng phương pháp Regularization, điều chỉnh mô hình sao cho giảm thiểu các vấn đề Overfitting, tối ưu hay kiểm soát mức độ phức tạp của mô hình để cân đối giữa Biased và Variance qua đó giảm sai số của mô hình. Công thức tổng quát của mô hình:
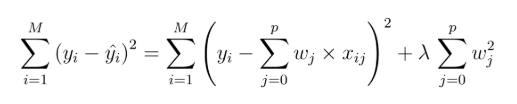
Hệ số lambda còn gọi là tham số Regularization, hay tham số Penalty, hay tham số Shrinkage, là số luôn dương, là giá trị mà ở đó phương trình tuyến tính sẽ được “tinh chỉnh” sao cho sai số của mô hình được giảm tối đa, nghĩa là giá trị lambda nào mà mô hình đạt MSE (Mean Square Error) sẽ được chọn, wj là hệ số β của phương trình hồi quy tuyến tính.
Cách triển khai công thức như thế nào, áp dụng phương pháp Regularization chúng tôi sẽ trình bày lại ở bài viết về Ridge Regression. Đồ thị minh họa:
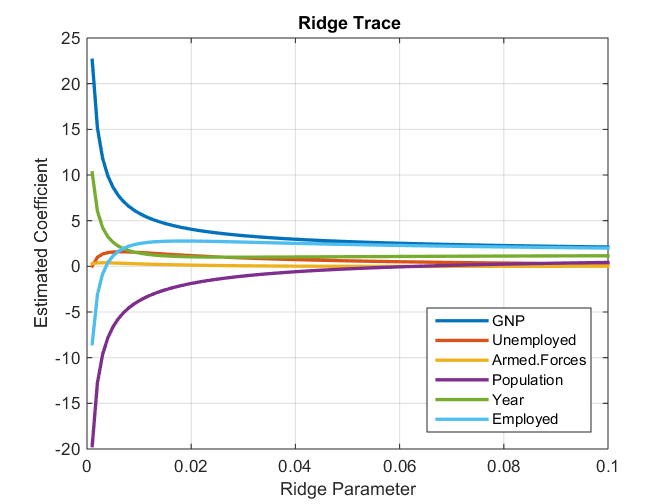
Nguồn hình: stats.stackexchange.com
- Lasso Regression
Lasso viết tắt của Least Absolute Shrinkage and Selection Operator, là phương pháp gần giống với Ridge Regression, cũng hạn chế sự khác biệt, chênh lệch giữa kết quả dự báo và kết quả thực tế của mô hình hồi quy tuyến tính, gia tặng độ chính xác của mô hình.
Công thức tổng quát của Lasso Regression khác một chút ở phía cuối công thức, thay vì bình phương wj, hay chính là hệ số β như Ridge Regression, thì ở đây công thức Lasso lấy trị tuyệt đối.
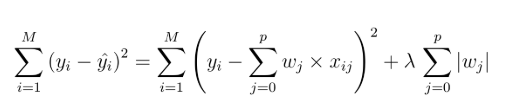
- Elastic Net Regression
Là mô hình hồi quy kết hợp mô hình Lasso và Ridge để xây dựng mô hình hồi quy xử lý vấn đề các biến độc lập x có mối quan hệ tương quan với nhau dẫn đến kết quả dự báo cho biến phụ thuộc y bị ảnh hưởng. Công thức tổng quát:
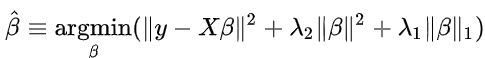
- Poisson Regression
Mô hình hồi quy Poisson áp dụng cho trường hợp biến phụ thuộc, biến y mang giá trị là các số đếm, tức biến định lượng dạng rời rạc có thể đếm được, ví dụ 0, 1, 2, 3, 4. Để áp dụng mô hình hồi quy Poisson thì giá trị của biến y phải có phân phối Poisson, và là số nguyên dương. Công thức phân phối Poisson của một giá trị x bất kỳ
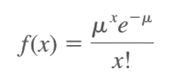
Với e là hằng số Nepe gần bằng 2.71828 µ là E(x) và là trung bình của x được tính bằng n*p, ở một số tài liệu thống kê khác µ chính là λ Giá trị kỳ vọng E(x) = µ = λ, phương sai Var (x) = λ = µ. Chúng ta áp dụng cho giá trị y thì được, P là xác suất của một giá trị y = k bất kỳ
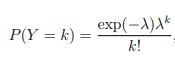
Ghép vào mô hình hồi quy với hệ số β và từng biến xi để xác định giá trị kỳ vọng cho từng giá trị của biến y. Phương trình tổng quát
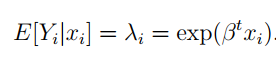
- Cox Regression
Mô hình hồi quy Cox áp dụng cho loại dữ liệu theo thời gian, được dùng trong phân tích sống sót “Survival analysis” ví dụ như phân tích rủi ro khách hàng rời dịch vụ theo thời gian, thời gian bệnh nhân tính từ lúc bệnh nhân bắt đầu điều trị ung thư cho đến khi qua đời,…Tức y lúc này có thể chỉ mang 2 giá trị “còn” và “không”, “sống” và “chết”, “đã rời dịch vụ” và “chưa rời dịch vụ”. Mô hình tổng quát của Cox regression sẽ có dạng:
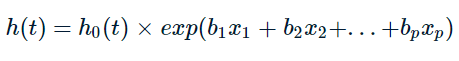
Với t là thời điểm xem xét khả năng “sống sót”, mô hình minh họa. h(t) là hàm nguy ở thời điểm t cho mỗi đối tượng dữ liệu, các biến x là biến độc lập cần xet, h0(t) là hàm nguy cơ khi tất cả các biến đều giải thích bằng 0 (trường hợp không xét tác động của các biến độc lập đến phụ thuộc y)
Đồ thị minh họa:
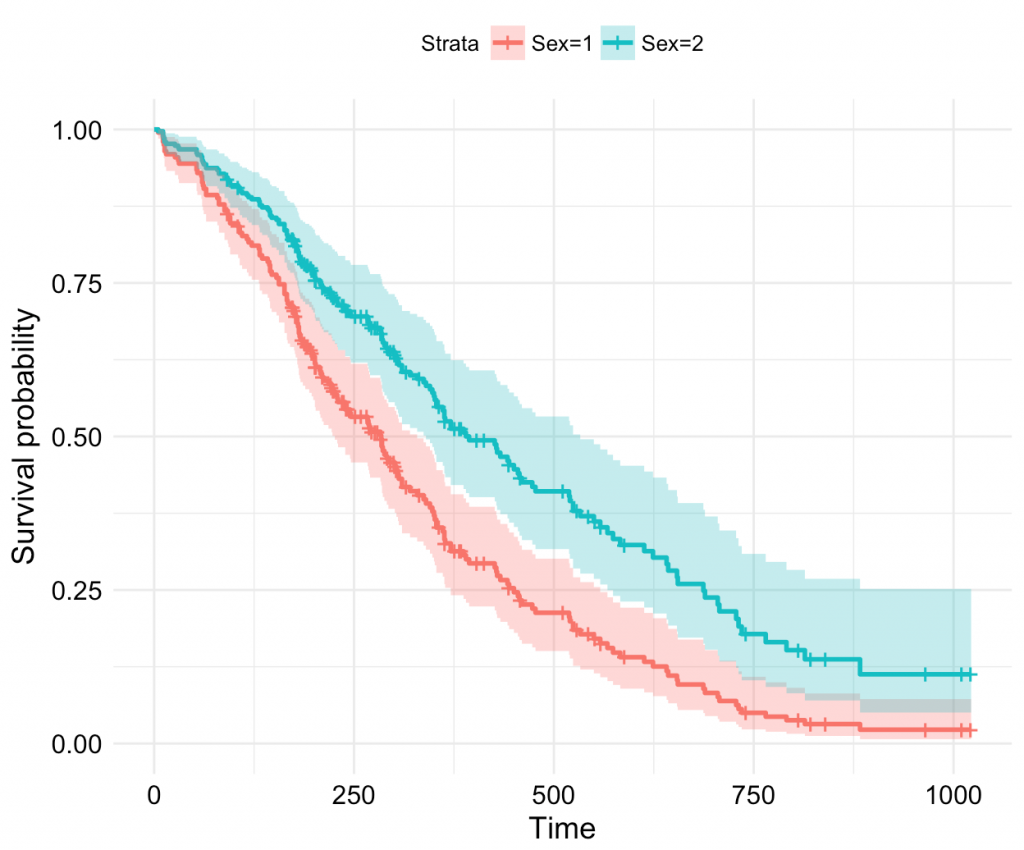
(nguồn hình: sthda.com)
Còn rất nhiều mô hình hồi quy khác mà chúng tôi không thể giới thiệu cũng như trình bày đầy đủ đến các bạn trong series bài viết về hồi quy như Principal Component Regression (PCR), Partial Least Squares Regression (PLS), Support Vector Regression,…các bạn có thể tham khảo thêm ở các tài liệu khác.
Trong bài viết tới, chúng ta sẽ đi vào tìm hiểu cách xây dựng mô hình hồi quy tuyến tính đơn giản với 1 biến x và 1 biến y, cũng như sử dụng phương pháp phấn tích tương quan để đánh giá mối quan hệ giữa 2 biến, nhưng trước hết chúng ta sẽ bàn về mục đích, ứng dụng của hồi quy trong các lĩnh vực khác nhau. Mong các bạn ủng hộ.
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English