Như vậy chúng ta đã cùng nhau đi qua 4 phần của series bài viết về thuật toán Decision trees hay còn gọi là thuật toán cây quyết định. Chúng ta đã làm quen với định nghĩa tổng quát, các dạng cây quyết định bao gồm phân 2 nhánh – CART, và nhiều nhánh C4.5 sử dụng các công thức Goodness of Split, Gini Index, Entropy kết hợp với Information Gain, hay Gain Ratio để xây dựng mô hình áp dụng cho biến mục tiêu là biến định tính, và chúng ta cũng tiếp cận qua một số cách thức để tăng độ hiệu quả của mô hình, tránh trường hợp Overfitting hay Underfitting như Stopping rule và Pruning method, và nhìn lại những ưu điểm, khuyết điểm một cách tổng thể về Decision Trees.
Trong bài viết lần này, và cũng là phần cuối của thuật toán cây quyết định, chúng ta còn 2 vấn đề cần xem xét đó chính là cách thức áp dụng mô hình Regression trees cho biến mục tiêu là dữ liệu định lượng liên tục – numeric (real numbers – số thực) hay continuous variable, và Decision rules – nguyên tắc diễn giải thuật toán cây quyết định.
Các kiến thức ở những bài viết trước chúng tôi sẽ không nhắc lại, và lưu ý thêm nếu các bạn chưa biết gì về phương pháp Classification, và Decision trees thì sẽ khó có thể tiếp thu được nội dung trong bài viết này. Những bạn nào chưa xem qua các bài viết trước của BigDataUni các bạn có thể tham khảo lại qua link dưới đây:
Thuật toán cây quyết định (P1) (CART)
Thuật toán cây quyết định cart (P2) (Gini index)
Thuật toán cây quyết định (P3) C4.5 (Entropy)
Thuật toán cây quyết định (P4) Ưu & khuyết điểm, Stopping Rule (Pruning method)
Regression Trees
Trước khi vào nội dung chính, chúng ta cùng đi qua cách thức phân nhánh cây quyết định cho từng loại biến khác nhau.
(Ví dụ trong phần này sau được tham khảo từ giáo trình Introduction to Data mining 2nd Edition, tác giả Tan, Steinbach, Karpatne, Kumar)
Đối với biến định tính cụ thể là biến định danh, ví dụ chúng ta sử dụng biến tình trạng hôn nhân bao gồm các giá trị: “Độc thân”, “Đã kết hôn”, “Đã ly hôn”.
- Dạng phân 2 nhánh:
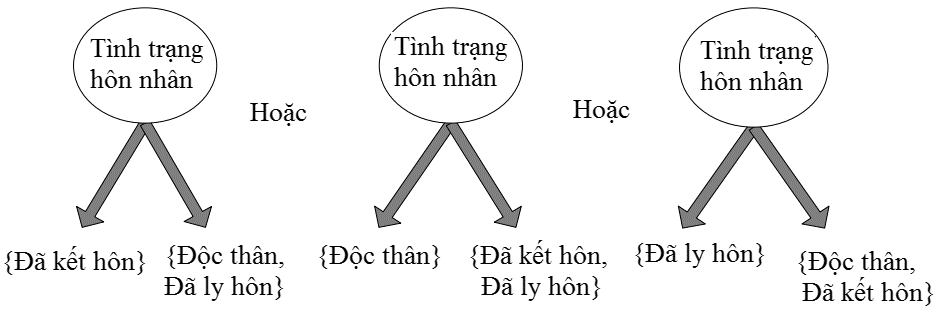
- Dạng phân nhiều nhánh:
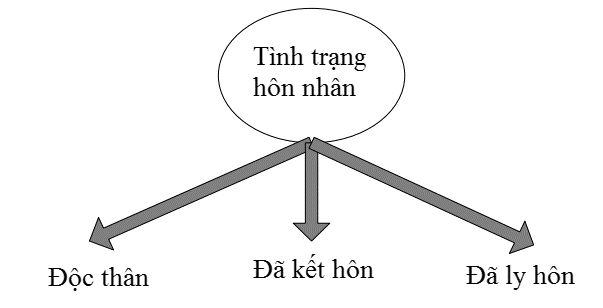
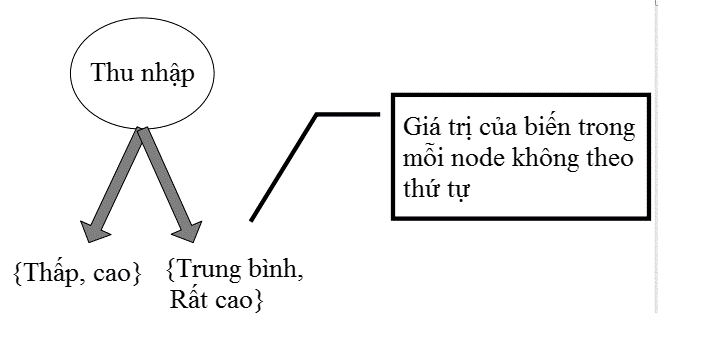
Đối với biến định tính cụ thể là biến thứ tự thì chúng ta cũng phân nhánh tương tự như biến định danh tuy nhiên cần giữ thứ tự giá trị từ bé đến lớn trong mỗi node.
- Dạng phân nhiều nhánh:
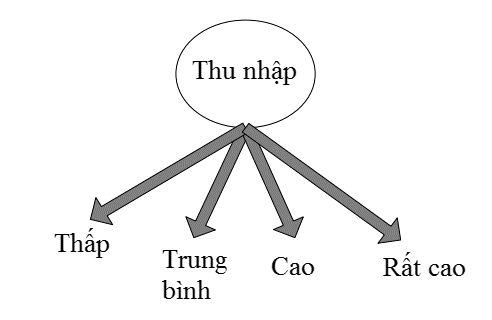
- Dạng phân 2 nhánh
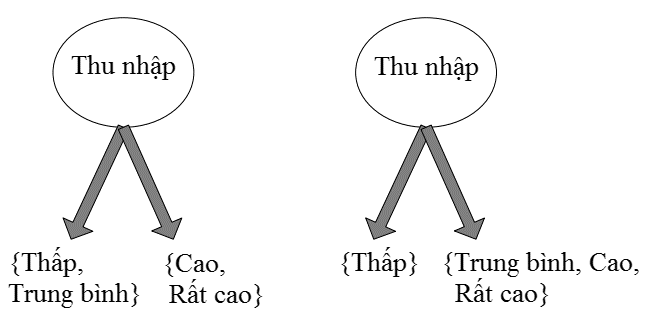
Các bạn có thể thấy ở các node tập hợp các đối tượng dữ liệu có giá trị có thể sắp xếp theo thứ tự ví dụ thấp đến trung bình, cao đến rất cao. Còn trường hợp dưới đây thì không nên thực hiện:
Đối với biến định lượng cụ thể là biến định lượng liên tục.
- Dạng phân 2 nhánh
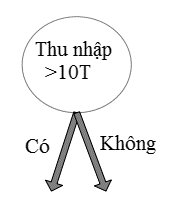
- Dạng phân nhiều nhánh
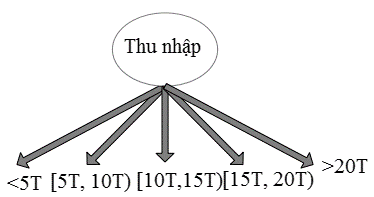
Các bạn quan sát, đối với biến dữ liệu là dạng biến định lượng chúng ta có thể phân tổ, một phương pháp trong thống kê trong việc biến đổi biến định lượng thành biến định tính để tóm tắt số liệu, hoặc nếu không sử dụng phương pháp thống kê, như phân 2 nhánh các bạn có thể linh hoạt phân dữ liệu thành 2 phần, đặt một giá trị làm mốc ví dụ ở trên các bạn sẽ có 2 nhánh với 1 nhánh thu nhập trên 10T và nhánh còn lại là dưới 10T. Cụ thể chúng ta có thể xử lý như sau:
- Phân nhóm cho dữ liệu định lượng chuyển đổi thành biến định tính hay biến thứ tự
+ Sắp xếp các giá trị theo thứ tự từ bé đến lớn
+ Phân nhóm theo khoảng cách đều tức chênh lệch giữa giá trị bé nhất và lớn nhất của nhóm này so với các nhóm khác là như nhau, giống ví dụ trên. Cách khác có thể kể đến như phân nhóm theo điều kiện tần số xuất hiện các đối tượng dữ liệu tại mỗi nhóm là như nhau ví dụ biến thu nhập: (5T – 8T) có 5 khách hàng, (8T – 15T) có 5 khách hàng, tương tự cho (15-20T) và trên 20T (với T là triệu đồng).
+ Nói về thời điểm phân nhóm trong khi xây dựng mô hình thì chúng ta có thể có 2 cách: phân nhóm 1 lần duy nhất (Static) ngay lúc trước khi xây dựng mô hình tức trước khi áp dụng các công thức để chọn root node (các bạn có thể xem lại các ví dụ trong những bài viết trước, để ý các biến định lượng), cách khác chính là tại mỗi lần phân nhánh, chúng ta phân nhóm (Dynamic), quá trình có thể lặp đi lặp lại và kết quả có thể khác so với những lần trước.
- Phân thành 2 khoảng, chọn 1 giá trị v bất kỳ, với A là giá trị bất kỳ của 1 đối tượng dữ liệu chúng ta sẽ có 2 nhóm (A < v) và (A ≥ v), trường hợp này áp dụng mô hình cây quyết định phân 2 nhánh, và để chọn ra giá trị v tối ưu nhất chúng ta phải xem xét đến các khả năng khác nhau, nhiều giá trị khác nhau, tiến hành phân tích ví dụ như áp dụng công thức Gini index, hay Entropy. Chính vì tính phức tạp, và cồng kềnh, phương pháp này tốn nhiều thời gian và chi phí tính toán nếu nó thực sự được triển khai trong thực tế.
Khác với biến định tính, mọi giá trị của biến định lượng đều có thể được chọn làm biến phân nhánh trong cây quyết định nên để tìm ra mô hình nào là tốt nhất để sử dụng phân loại cho các đối tượng dữ liệu là vấn đề khó khăn hơn nhiều, do đó thông thường chúng ta sẽ cố gắng chuyển đổi biến định lượng thành định tính, và vô tính giới hạn khả năng, và hiệu suất của mô hình. Đây chính là khuyết điểm của Decision trees.
Đề cập một chút về cái tên Regression Trees, là thuật ngữ chúng ta nói đến khi áp dụng mô hình cây quyết định cho biến định lượng. Nhớ lại bài viết phần 1, BigDataUni có trình bày đến các bạn một tên gọi khác cho Decision Trees và phổ biến hơn trong một số giáo trình Data mining quốc tế đó chính là Classification & Regression Trees (tránh nhầm lẫn với CART, đây là tên gọi chung). Cái tên này xuất phát từ ứng dụng của chính các thuật toán cây quyết định. Ứng dụng thứ 1: Classification tree, chúng ta đã biết là phân loại đối tượng vào các lớp, các nhóm dựa trên biến mục tiêu đã cho trược từ đó. Ứng dụng thứ 2: Regression tree, dự báo giá trị có thể có của biến mục tiêu là biến định lượng. Ứng dụng thứ 2 của cây quyết định gần giống như phương pháp phân tích hồi quy, Regression analysis, bao gồm phổ biến như Linear Regression, Logistic Regression, Multi-linear Regression, v.v, phân tích mối quan hệ, mức độ liên hệ, tính bền vững trong mối quan hệ tuyến tính giữa các biến đầu vào và biến mục tiêu (dựa vào dữ liệu lịch sử), lấy đó làm cơ sở để dự báo giá trị của biến mục tiêu cho đối tượng dữ liệu.
Đối với Classification thì chúng ta đơn giản phân loại đối tượng thông qua các công thức phân nhánh không quá phức tạp mà không cần quan tâm nhiều đến mối quan hệ giữa các biến với biến mục tiêu. Tuy nhiên ngược lại với Regression chúng ta không biết chắc chắn giá trị nào của biến mục tiêu mà đối tượng dữ liệu có thể nhận, và phải quan tâm đến mối quan hệ giữa toàn bộ các biến, vì nó sẽ ảnh hưởng đến giá trị sau cùng. Ở phân tích hồi quy, thì chúng ta có thể thấy rõ vấn đề này nhờ vào phương trình hồi quy tổng quát, và tính toán đưa ra kết quả sau cùng. Mặc dù không thể hiện rõ mức độ quan hệ hay liên quan giữa các biến như thế nào, nhưng thuật toán cây quyết định phần nào vẫn giúp chúng ta thấy được biến nào có thể tác động lên biến mục tiêu.
Tiếp theo chúng ta cùng đi qua vào ví dụ cụ thể. Ví dụ đầu tiên (được tham khảo từ giáo trình Introduction to Data mining 2nd Edition, tác giả Tan, Steinbach, Karpatne, Kumar) là chúng ta đã xác định được node phân nhánh là một biến định lượng, thu nhập cá nhân hàng năm (USD), tiếp theo chúng ta cần phân 2 nhánh cho node này cụ thể để xây dựng cây quyết định dạng Binary splits, tìm kiếm các giá trị v, và xét xem có bao nhiêu khách hàng có thu nhập ≤ v có khả năng rủi ro tín dụng, và không có rủi ro tín dụng, tương tự xét cho khách hàng có thu nhập > v
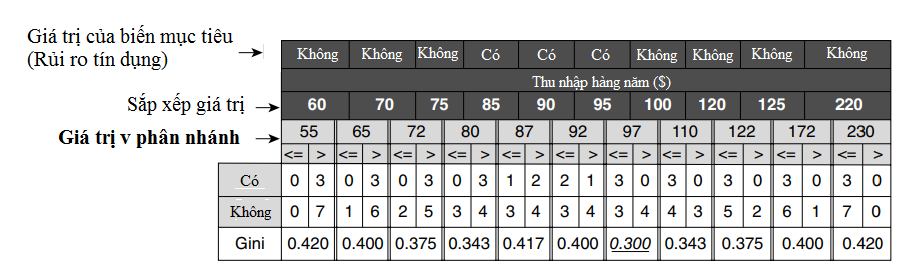
Giả sử chúng ta có số liệu về thu nhập hàng năm của 10 khách hàng (tính theo 1000$) như trên, sắp xếp số liệu theo thứ tự từ bé đến lớn, giá trị v chúng ta lấy sẽ là trị số giữa giữa 2 giá trị thu nhập liền kề, tức giữa 60 và 70 giá trị v là 65, giữa 75 và 70 là 72.5, chúng ta có thể làm tròn lên hoặc giữ nguyên giá trị 72. Tiếp theo tại mỗi giá trị chúng ta sẽ kiểm tra có báo nhiêu khách hàng có thu nhập cao hơn giá trị này, và thấp hơn giá trị này, có bao nhiêu khách hàng sẽ có rủi ro tín dụng, và không có rủi ro tín dụng. Ví dụ tại giá trị v = 55, có 10 khách hàng đều có thu nhập trên 55.000$, trong 10 khách hàng này có 3 khách hàng có rủi ro tín dụng, 7 khách hàng không có rủi ro tín dụng. Lưu ý với các bạn nào chưa biết thì dữ liệu áp dụng cho mô hình cây quyết định là dữ liệu lịch sử, như ví dụ này là dữ liệu về các khách hàng đã được đánh giá rủi ro tín dụng, những đặc điểm của các khách hàng này thông qua cây quyết định sẽ được trực quan và sẽ là cơ sở để chúng ta đánh giá cho khách hàng mới. Quay lại với các số liệu trên, tại giá trị v = 65, chúng ta có 1 khách hàng có thu nhập thấp hơn 65.000 $ không có rủi ro tín dụng, và 9 khách hàng có thu nhập hơn 65.000 $ trong đó có 6 khách hàng không có rủi ro tín dụng và 3 khách hàng có rủi ro tín dụng. Như vậy, các bạn tiếp tục xét cho đến giá trị v = 230.
Tiếp theo chúng ta sẽ sử dụng công thức Gini index để tính Impurity, mức độ đồng nhất của node phân nhánh, nhắc lại công thức các bài viết trước:
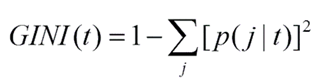
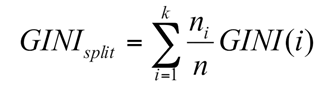
Gini (x > 55) = 1 – (3/10)2 – (7/10)2 = 0.42
Gini (x ≤ 55) = 0
GiniSplit (55) = 0*0 + 1*0.42 = 0.42
Gini (x > 60) = 1 – (3/9)2 – (6/9)2 = 0.444
Gini (x ≤ 60) = 1 – (1/1)2 = 0
GiniSplit (60) = 0*(1/10) + (9/10)*0.444 = 0.4
Các bạn tính tương tự cho đến node sau cùng là 230, và chọn là giá trị v nào sẽ đem lại giá trị GiniSplit bé nhất. Quan sát trên bảng số liệu tính sẵn, chúng ta thấy giá trị v = 97 có GiniSplit bé nhất nên có thể được chọn để phân nhánh. Đây là phương pháp đơn giản và dễ hiểu. Một cách tiếp cận khác có thể giúp quá trình tính toán diễn ra nhanh hơn. Như các bạn thấy trên bảng số liệu thì các khách hàng có thu nhập từ 60.000 $ đến 75.000 $ sẽ không có rủi ro tín dụng, mà chúng ta phân loại cho khách hàng mới chúng ta phải quan tâm đến cả trường hợp có rủi ro tín dụng nên tối ưu nhất, và tốt hơn thì chúng ta nên chọn v mà v là trung bình giữa 2 giá trị thu nhập không chứa cùng giá trị biến mục tiêu. Ví dụ v = 72 được tính từ 75 và 70 mà cả 2 giá trị này đều không có rủi ro tín dụng, v = 80 được tính từ 75, và 80, một có rủi ro, một không rủi ro.
Lúc này v = 80 được ưu tiên để xét, như vậy từ 11 giá trị v chúng ta sẽ ưu tiên xét có 2 giá trị là v = 80 và v = 97, so sánh GiniSplit để chọn tiếp v = 97, quá trình diễn ra nhanh hơn.
Ví dụ ở trên là chúng ta đang xét đến trường hợp node này là Internal node có thể áp dụng biến mục tiêu là biến định tính vậy nếu biến mục tiêu là biến định lượng thì nên xử lý như thế nào? Có nên chuyển đổi sang dạng định tính rồi làm như bình thường hay không? Có cách tiếp cận khác trong việc tính toán đó chính là độ lệch chuẩn (Standard Deviation) và giá trị giảm thiểu độ lệch chuẩn mỗi node phân nhánh (Standard Deviation Reduction – SDR). Việc phân nhánh trong lúc xây dựng mô hình cây quyết định đó chính là việc phân chia tập dữ liệu thành các tập con trên cơ sở chúng sẽ đồng nhất về giá trị sau cùng của biến mục tiêu. Nếu tất cả các đối tượng dữ liệu trong node đồng nhất về giá trị của biến mục tiêu, thì độ lệch chuẩn sẽ bằng 0. Nhắc lại một số kiến thức về độ lệch chuẩn, trước tiên là phương sai.
Phương sai là trung bình cộng của bình phương các độ lệch giữa các giá trị của từng quan sát và số trung bình cộng (Mean) của dãy số. Độ lệch chuẩn chính là căn bậc 2 của phương sai. Phương sai lớn phản ánh khuynh hướng phân tán nhiều, và độ biến thiên cao của dữ liệu, độ lệch chuẩn đại diện cho một giá trị trung bình, là chênh lệch giữa giá trị của mỗi quan sát so với trung bình cộng của dãy số, do đó cũng thể hiện được độ biến thiên, độ lệch chuẩn càng cao thì dãy số phân tán nhiều và ngược lại. Do đó nếu trong một node, các đối tượng dữ liệu có giá trị định lượng của biến mục tiêu quá chênh lệch hay khác biệt, thi SD sẽ rất lớn, cách phân nhánh này có thể không hiểu quả, và ngược lại. Với biến mục tiêu là biến định tính, chúng ta có trước giá trị của biến mục tiêu và có thể xem xét các biến khác tác động như thế nào đến biến mục tiêu để tìm ra quy luật ra quyết định, xây dựng mô hình phân loại. Với biến mục tiêu là biến định lượng chúng ta không thể có ngay giá trị của biến mục tiêu, mà phải đi tìm mối liên hệ giữa các biến khác với biến mục tiêu để xác định giá trị biến mục tiêu có thể là giá trị chung nhất của các đối tượng dữ liệu có cùng một số đặc điểm nhất định. Giá trị của biến mục tiêu sau cùng tại các leaf node sẽ là giá trị trung bình của các đối tượng dữ liệu bên trong node.
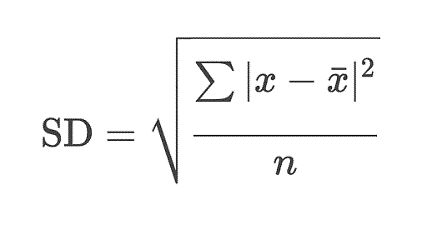
SDR sẽ bằng độ lệch chuẩn của các giá trị biến mục tiêu xét trên toàn bộ quan sát trừ cho SD tổng quát của mỗi node. SDR càng lớn thì cách phân nhánh càng tối ưu.
Phương pháp đánh giá mô hình Regression Trees đó chính là sử dụng công thức RMSE (Root Mean Square Error), công thức cốt lõi trong việc xác định tính hiệu quả của các phương trình Regression, phương trình hồi quy và cả mô hình Time Series trong thống kê.
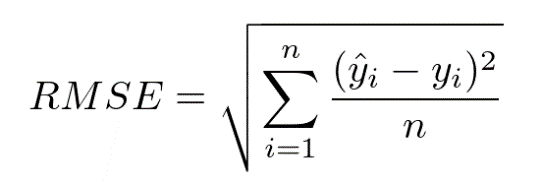
RMSE chính là tính toán mức độ chênh lệch giữa giá trị dự báo và giá trị quan sát thực tế, RMSE càng nhỏ thì mô hình càng hiệu quả.
Các bạn lưu ý ở một số tài liệu họ sẽ không dùng SD mà sử dụng các công thức khác như Sum of Squares (SS), Sum of Square Errors (SSE), hay Sum of Square Deviation (SSD), về nguyên lý thì nó gần giống nhau.
Chúng ta sẽ thử áp dụng công thức độ lệch chuẩn để chọn cách phân nhánh cho cây quyết định.
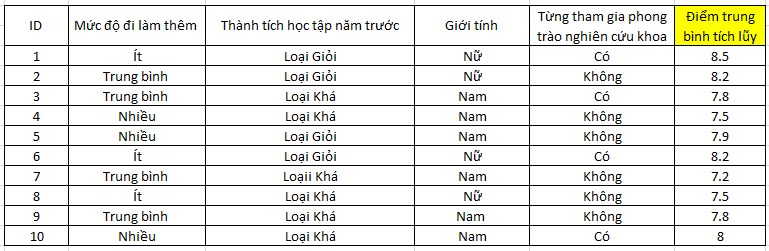
Giả sử chúng ta có dữ liệu về 10 sinh viên, với biến mục tiêu là “Điểm trung bình tích lũy”, chúng ta sẽ xây dựng mô hình Regression Trees để tìm hiểu xem các biến đầu vào sẽ tác động như thế nào đến mục tiêu sau cùng. BigDataUni sẽ ví dụ thử xác định cách phân nhánh đầu tiên, các lần phân nhánh tiếp theo các bạn có thể tự xử lý.
SD của biến mục tiêu xét cho cả tập dữ liệu = 0.369 (các bạn áp dụng công thức phía trên)
Mức độ đi làm thêm = ít, có 3 sinh viên, điểm TBTL lần lượt là 8.5, 8.2, 7.5. SD (ít) = 0.42, tương tự xét cho mức độ đi làm thêm = trung bình và nhiều, SD (TB) = 0.357, SD (Nhiều) = 0.216
SD (mức độ đi làm thêm) có trọng số = (3/10)*0.42 + (4/10)*0.357 + (3/10)* 0.216 = 0.333
SDR (mức độ đi làm thêm) = 0.369 – 0.333 = 0.036
Các bạn tự tính tiếp cho các biến còn lại thì sẽ được:
SDR (Thành tích học tập) = 0.369 – 0.242 = 0.126
SDR (Giới tính) = 0.369 – 0.309 = 0.06
SDR (Tham gia HĐNCKH) = 0.369 – 0.26 = 0.1
Như vậy chúng ta sẽ chọn biến Thành tích học tập để phân nhánh đầu tiên. Vấn đề đặt ra là khác với cây quyết định áp dụng cho biến mục tiêu là biến định tính, chúng ta sẽ không phân nhánh nếu node đó là pure node, hay terminal node, tức các đối tượng dữ liệu có chung giá trị của biến mục tiêu. Nhưng ở biến định lượng chúng ta không thể xác định như vậy mà thay vào đó tự phải đặt ra một số yêu cầu như nếu tổng số đối tượng của 1 node không vượt quá ngưỡng giá trị n (tùy theo kinh nghiệm, kiến thức của người phân tích) nào đó thì chúng ta không tiếp tục phân nhánh cho node này, hoặc áp dụng công thức hệ số biến thiên:
Coefficient of Variation (CV) = (SD/trung bình x)*100%
Hệ số biến thiên CV so sánh mức độ phân tán giữa các tập dữ liệu, mà mức độ phân tán là sự chênh lệch của các giá trị trong tập dữ liệu so với giá trị trung bình của chính tập dữ liệu ấy. Nếu CV càng lớn tức biến thiên càng nhiều, nghĩa là các đối tượng dữ liệu trong node không đồng nhất, cần phải xét tiếp. Nếu CV của node này lớn hơn node kia, thì node này không có sự đồng nhất giữa các đối tượng dữ liệu, cần phân nhánh tiếp.
Quay trở lại với ví dụ, như vậy Thành tích học tập sẽ là root node và phân ra 2 nhánh, 1 bên là khá và 1 bên là giỏi, vậy tiếp theo chúng ta sẽ lấy node “Thành tích học tập = khá”, hay “Thành tích học tập = giỏi” để phân nhánh tiếp? Các bạn thử áp dụng công thức CV để tính nhé. Lưu ý lần nữa khi node nào không thể phân nhánh tiếp thì bạn hãy tính giá trị trung bình của điểm TBTL trong node ấy, đấy sẽ là giá trị sau cùng của biến mục tiêu
Decision rules
Một trong những điểm hấp dẫn nhất của thuật toán cây quyết định đó chính là khả năng diễn giải mô hình dựa trên việc sử dụng quy luật ra quyết định (Decision rules). Vậy Decesion rules được lấy ở đâu? Chính là lấy từ hay trích xuất từ thuật toán cây quyết định sau khi đã được xây dựng. Dựa trên nguyên lý nếu…thì… (IF – THEN), mỗi quyết định sẽ được xuất phát từ Root node, đến các node bên trong Internal node thông qua các nhánh để đến với các lá sau cùng Leaf node hay Terminal node. Một tập hợp các quyết định đưa ra sẽ tương đồng với cách thức phân loại của cây quyết định.
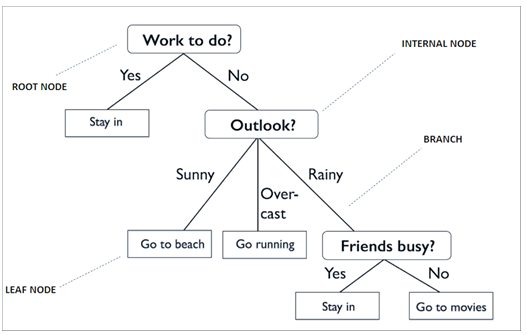
Để hiểu rõ hơn chúng ta cùng lấy lại ví dụ từ bài viết C4.5 sử dụng Entropy.
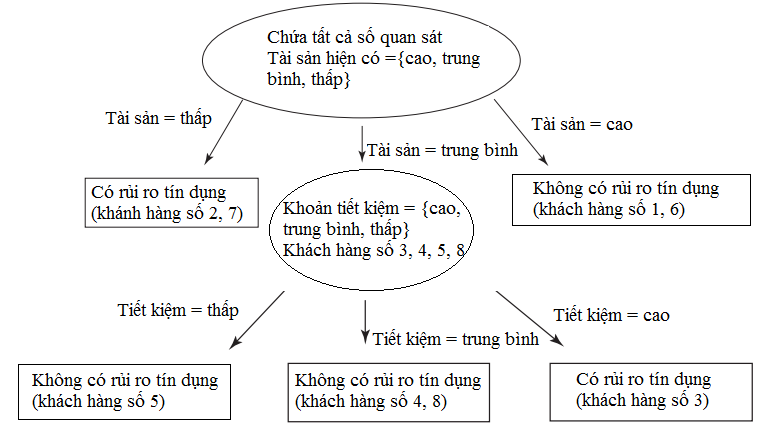
Quy luật quyết định như sau:
- Nếu giá trị tài sản thấp, thì có rủi ro tín dụng, tỷ lệ Support cho quyết định này là (2/8), số quan sát có giá trị biến mục tiêu “Có rủi ro tín dụng” là 2 trên tổng số quan sát là 8. Confidence có giá trị là 1, nghĩa là trong node này 100% khách hàng có rủi ro tín dụng
- Nếu giá trị tài sản cao, thì không có rủi ro tín dụng, tỷ lệ Support là (2/8), Confidence là 1
- Nếu giá trị tài sản trung bình và khoản tiết kiệm thấp thì không có rủi ro tín dụng, tỷ lệ Support là (1/8), Confidence là 1.
- Nếu giá trị tài sản trung bình và khoản tiết kiệm trung bình thì không có rủi ro tín dụng, tỷ lệ Support là (2/8), Confidence là 1.
- Nếu giá trị tài sản trung bình và khoản tiết kiệm cao thì không có rủi ro tín dụng, tỷ lệ Support là (2/8), Confidence là 1.
Do ở ví dụ trên các node đều thuần khiến, các khách hàng hay đối tượng dữ liệu đều mang cùng 1 giá trị của biến mục tiêu, không có thông tin hỗn độn khác nên Confidence đều là 1, trong thực tế thì không có như vậy, đối với trường hợp khối lượng dữ liệu nhiều, phức tạp, nhiều biến khác nhau thì đạt được tỷ lệ Confidence hoàn hảo như trên là rất khó.
Đến đây là kết thúc series các bài viết về thuật toán cây quyết định, mong rằng qua chuỗi các bài viết này các bạn sẽ nắm cơ bản được thuật toán Decision Trees là gì, và cách thức triển khai. Ở các bài viết sắp tới chúng ta sẽ sang các mô hình Regression, mong các bạn tiếp tục ủng hộ BigDataUni.
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English