Trở lại với chủ đề phân tích phương sai, bài viết trước chúng ta đã tìm hiểu về khái niệm, mục đích cũng như cách vận hành của ANOVA, chúng ta cũng đã đi qua dạng ANOVA đầu tiên – One – way ANOVA áp dụng cho việc tìm hiểu tác động, sự ảnh hưởng của 1 yếu tố nguyên nhân đến kết quả, đến đối tượng nghiên cứu với ví dụ cụ thể trong lĩnh vực kinh tế.
Ở bài viết phần 2 cũng là bài viết cuối cùng về ANOVA, BigDataUni và các bạn tiếp tục ANOVA 1 yếu tố nhưng với hướng tiếp cận khác trong nghiên cứu, và đến với Two-way ANOVA – phân tích ANOVA cho 2 yếu tố tác động.
Lưu ý, những bạn nào chưa biết gì, hay không có kiến thức gì về phân tích phương sai thì nên tham khảo trước ở các tài liệu khác hoặc qua bài viết phần 1 của chúng tôi:
Phân tích phương sai – ANOVA (analysis of variance) (P.1)
Tóm tắt ngắn nội dung bài viết phần 1:
Động cơ của phương pháp phân tích phương sai chính là so sánh giá trị trung bình của các tổng thể, và khi các tham số tổng thể là chưa biết, chúng ta sẽ sử dụng các trung bình mẫu để so sánh, kết hợp với phương pháp kiểm định giả thuyết, để đưa ra các kết luận sau cùng về các tổng thể, cụ thể là rốt cuộc có hay không có tác động của một yếu tố nào đó lên đối tượng nghiên cứu hay yếu tố nguyên nhân nào đó lên kết quả mong đợi.
Nếu các trung bình tổng thể nằm gần nhau trên đồ thị phân phối xác suất thì khả năng chúng chỉ thuộc một tổng thể duy nhất, từ đó suy ra các cấp độ, các thuộc tính của yếu tố nguyên nhân, của yếu tố tác động không ảnh hưởng lên đối tượng nghiên cứu, giữa chúng không có mối quan hệ, và ngược lại.
Để xác định được các trung bình tổng thể trong thực tế có gần nhau hay không thì từ các mẫu dữ liệu lấy ra trong các tổng thể, ANOVA sử dụng các công thức toán để tính toán mức độ chênh lệch giữa các trung bình mẫu, giữa các giá trị,…tiếp đến là tìm phương sai và sau cùng tích hợp phương pháp kiểm định giả thuyết để kiểm chứng các giả thuyết liên quan đến sự bằng nhau của các trung bình tổng thể.
Tóm tắt các bước triển khai ANOVA – 1 yếu tố, các bạn lưu ý một số bước dưới đây có trong ANOVA – 2 yếu tố mà chúng tôi sẽ đề cập ở phần sau bài viết:
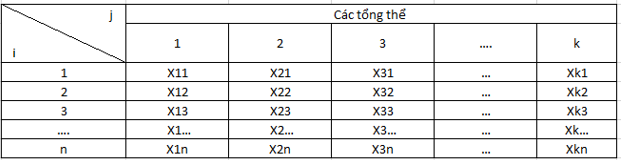
- Đặt giả thuyết:
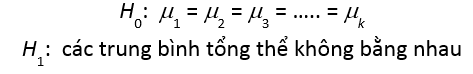
- Tính trung bình của từng nhóm
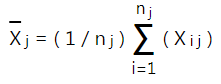
- Tính trung bình của tất cả các nhóm (trung bình chung toàn tập dữ liệu)
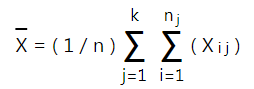
- Tính tổng các bình phương chênh lệch giữa các giá trị trong mỗi nhóm với trung bình của chính nhóm đó
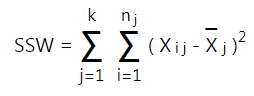
- Tính tổng các bình phương chênh lệch của trung bình nhóm so với trung bình chung ở bước 2:
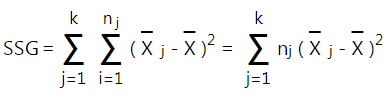
- Tính tổng chênh lệch bình phương của các giá trị trong tập dữ liệu so với trung bình chung ở bước 2:
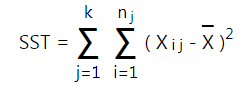
Ngoài ra: SST = SSG + SSW
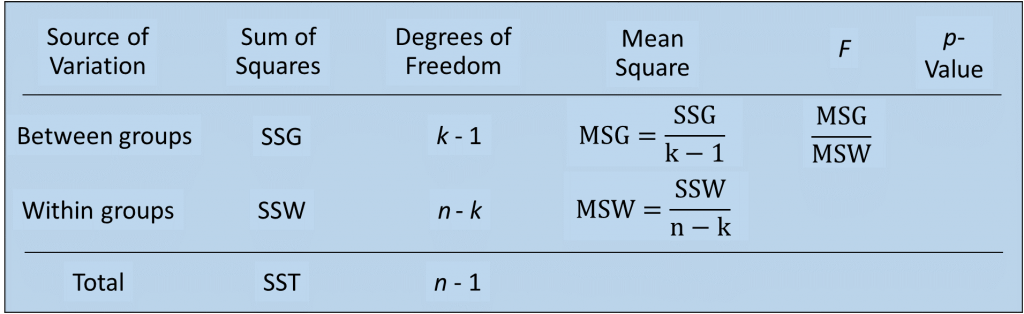
- Tính phương sai, hay tính trung bình của các chênh lệch bình phương tìm được
MSW = SSW/ (n – k)
MSG = SSG/ (k – 1)
- Tính giá trị kiểm định F
F = MSG/ MSW
Bác bỏ H0, tức các trung bình tổng thể không bằng nhau, kết luận yếu tố tác động có ảnh hưởng lên đối tượng nghiên cứu khi:
F > Fk – 1, n – k, α
Các bạn xem lại ví dụ ở bài viết phần 1, thì sẽ cảm thấy các công thức trên rất đơn giản, dễ nhớ một cách nhanh chóng, đặc biệt bạn nào chưa biết gì về ANOVA thì càng nên xem lại.
Hướng tiếp cận khác trong ANOVA – 1 yếu tố
Quay trở lại với ví dụ ở bài viết phần 1:
Một công ty bán lẻ toàn cầu có hơn 2000 cửa hàng phân bổ ở gần tất cả các bang trên nước Mỹ, vừa phát triển 4 phương pháp hay còn gọi là mô hình trưng bày hàng hóa, bán hàng, và cung cấp dịch vụ tại các cửa hàng.
- Phương pháp 1: thay đổi cách trưng bày hàng hóa thông thường hay truyền thống theo hướng hiện đại (ứng dụng phân tích dữ liệu)
- Phương pháp 2: thay đổi cách thức hỗ trợ khách hàng, ân cần, thân thiết hơn với phong cách phục vụ chuyên nghiệp
- Phương pháp 3: thay đổi thiết kế toàn bộ không gian hàng hóa, cải thiện môi trường không khí bên trong cửa hàng.
- Phương pháp 4: tích hợp robot hỗ trợ bán hàng bên cạnh thay đổi thiết kế gian hàng, cách trưng bày hàng hóa để tối đa thu hút khách hàng.

Công ty chọn tiểu bang đông dân nhất của nước Mỹ, California, cũng là nơi có nhiều cửa hàng nhất để chọn ra một số cửa hàng ngẫu nhiên. Mỗi phương pháp sẽ chọn ngẫu nhiên 6 cửa hàng để áp dụng, doanh thu tháng đầu tiên của mỗi cửa hàng sẽ được ghi lại.
Gọi µ1, µ2, µ3, µ4 lần lượt là doanh thu trung bình của các cửa hàng ứng với phương pháp 1 đến 4. Giả thuyết H0 cho rằng doanh thu trung bình của các cửa hàng là bằng nhau, tức việc thay đổi phương pháp
H0: µ1 = µ2 = µ3 = µ4
H1: ít nhất có 2 trung bình doanh thu tổng thể khác nhau
Ở bài viết phần 1 chúng ta đã sử dụng ANOVA 1-yếu tố để phân tích mối quan hệ của các phương pháp áp dụng với doanh thu trung bình của các cửa hàng và thấy rằng các phương pháp có tác động rõ rệt (giả thuyết H0 đã bị bác bỏ). Và trong số các phương pháp đó, thì các cửa hàng nào ứng dụng robot hỗ trợ bán hàng bên cạnh thay đổi thiết kế gian hàng, cách trưng bày hàng hóa để tối đa thu hút khách hàng có doanh thu cao hơn so với các cửa hàng còn lại.
Tuy nhiên câu hỏi đặt ra ở đây là sự khác biệt trong doanh thu có phải chỉ do các phương pháp áp dụng, có thể do yếu tố khác mà chúng ta chưa đề cập đến? Ví dụ ngay cả quy mô các cửa hàng khác nhau, lượng hàng hóa được bán tại các cửa hàng khác nhau, mức độ tiêu dùng cửa người dân, của khách hàng cũng khác nhau do có thể các cửa hàng cùng bang California nhưng nằm ở các thành phố khác nhau thì sao?
Vì lấy mỗi phương pháp lấy ngẫu nhiên 6 cửa hàng để áp dụng, tổng cộng 24 cửa hàng ngẫu nhiên trong số rất nhiều cửa hàng tại bang California.
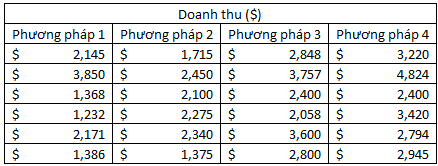
Các bạn nhìn trên bảng dữ liệu có thể thấy, ở phương pháp thứ nhất có cửa hàng doanh thu tháng đầu tiên 3.8 triệu USD, chênh lệch lớn so với cửa hàng còn lại, và hơn cả một số cửa hàng ở phương pháp 4 nguyên nhân là do đâu? Và ở phương pháp thứ 3 và thứ 4 cũng vậy, các cửa hàng có doanh thu cao nhất và thấp nhất chênh lệch khá nhiều.
Thực chất, ở từng phương pháp, các cửa hàng có doanh thu không đồng đều. Dẫn đến SSW có thể lớn, MSW cũng có thể lớn, F = MSG/ MSW sẽ nhỏ, nguy cơ không bác bỏ H0 sẽ cao, tức các trung bình tổng thể sẽ bằng nhau, kết luận các phương pháp không ảnh hưởng lên doanh thu.
Tuy kết quả kiểm định cho thấy bác bỏ H0, nhưng sự khác biệt trong doanh thu ở mỗi nhóm, có thể do một nguyên nhân khác không đề cập trong quá trình nghiên cứu, và nguyên nhân này nguy cơ vô tình ảnh hưởng lên các trung bình mẫu, chênh lệch bình phương, hay phương sai tính được, sau cùng là giá trị kiểm định có thể không được chính xác. Nếu chúng ta thu thập ngẫu nhiên thêm các cửa hàng và cho thử nghiệm ngẫu nhiên mỗi cửa hàng 1 phương pháp, giống bài toán lúc đầu thì khả năng không bác bỏ H0 là rất cao.
Công ty từ đó sẽ hiểu nhầm là các phương pháp không có ý nghĩa để đưa vô thử nghiệm, thế nhưng thực tế là chúng có mang lại sự khác biệt.
Để hạn chế vấn đề trên thì công ty phải:
- Một là xác định các cửa hàng có tính chất giống nhau và xếp chung vào một nhóm, sau đó các nhóm đã xác định, rồi mới áp dụng cả 4 phương pháp cho từng nhóm để xem sự khác biệt và mỗi nhóm chọn ra ngẫu nhiên 1 cửa hàng để thu thập dữ liệu.
- Hai là đơn giản chọn ra ngẫu nhiên một số cửa hàng và mỗi cửa hàng đều được áp dụng cả 4 phương pháp
Đây được coi là hướng tiếp cận khác trong ANOVA, hướng tiếp cận khác ở đây là cách phát triển quy trình nghiên cứu. Trong các tài liệu thống kê quốc tế, các chuyên gia còn gọi 2 phương pháp nghiên cứu phổ biến trong ANOVA:
Phương pháp 1: Completely randomized design, hoàn toàn ngẫu nhiên. Ví dụ 24 cửa hàng được chọn ngẫu nhiên, ở mỗi phương pháp sẽ chọn ra 6 cửa hàng ngẫu nhiên để áp dụng
Phương pháp 2: Randomized block design, ngẫu nhiên theo nhóm. Ví dụ (ở dấu chấm thứ 2 ở trên) các cửa hàng được chọn ngẫu nhiên, mỗi cửa hàng đại diện cho 1 block, và mỗi block sẽ được áp dụng cả 4 phương pháp; (ở dấu chấm thứ 1 ở trên), các cửa hàng ngẫu nhiên sẽ được xếp vào các nhóm, hay các block mà ở đó chúng có đặc điểm khác nhau, mỗi block sẽ được áp dụng cả 4 phương pháp.
Mục đích sử dụng Randomized block design làkiểm soát những yếu tố không đề cập trong nghiên cứu mà có ảnh hưởng lên kết quả phân tích. Trong phương pháp này các đơn vị quan sát giống nhau sẽ được xếp vào một khối, hoặc một đơn vị quan sát đóng vai một khối, sẽ hạn chế bớt số đơn vị quan sát mà có các giá trị có thể chênh lệch nhau do các yếu tố không liên quan. Các bạn sẽ hiểu hơn khi vào phần ví dụ.
Ở dấu chấm thứ nhất chúng tôi sẽ trình bày ở phần ANOVA – 2 yếu tố, do khi các cửa hàng có doanh thu khác nhau được xếp theo nhóm, tức các tính chất của nhóm có thể coi là yếu tố thứ 2 sau yếu tố thứ 1 là các phương pháp cũng tác động lên doanh thu.
Quay trở lại vấn đề ở trên:
Công ty giờ đây nhận thấy được vấn đề phát sinh như đã nói ở trên, họ thay đổi cách thức nghiên cứu, chọn ngẫu nhiên 6 cửa hàng, mỗi cửa hàng sẽ được áp dụng không theo trình tự cả 4 phương pháp, mỗi phương pháp sẽ được áp dụng trong 1 tuần và được ghi nhận doanh thu.
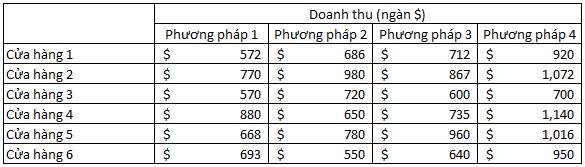
Chúng ta sẽ đi vào từng bước:
- Đặt giả thuyết
Cách đặt giả thuyết không có gì khác biệt:
H0: µ1 = µ2 = µ3 = µ4
H1: ít nhất có 2 trung bình doanh thu tổng thể (phương pháp) khác nhau
Bác bỏ H0, nghĩa là các phương pháp có tác động lên doanh thu của từng cửa hàng
- Tính trung bình
Cách tính trung bình cũng giống như ví dụ đầu tiên. Chúng ta cũng sẽ tính trung bình mỗi nhóm, trung bình chung các nhóm, các bạn xem lại công thức ở đầu bài viết.
Nhưng ở đây chúng ta cần tính thêm trung bình theo mỗi dòng, hiểu đơn giản, trung bình doanh thu mỗi cửa hàng (nếu xem mỗi cửa hàng là block, thì là trung bình mỗi block), công thức như sau:
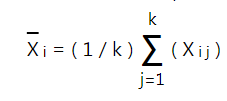
K là số cột, i là thứ tự block, ở đây là thứ tự cửa hàng.
Kết quả thu được như sau
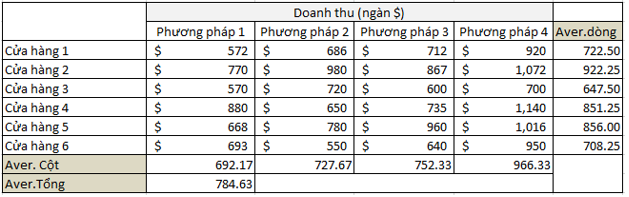
Ví dụ
Xpp1 = (572 + 770 + 570 + 880 + 668 + 693)/6 = 692.17
Xch1 = (572 + 686 + 712 + 920)/4 = 722.5
Xchung = (692.17 + 727.67 + 752.33 + 966.33)/4 = 784.63 (hoặc các bạn tính doanh thu trung bình từ 24 giá trị trên)
- Tính tổng các chênh lệch bình phương
Khác với lần đầu triển khai, theo công thức ANOVA áp dụng cho trường hợp này, chúng ta sẽ không tính SSW tức không tính tổng các bình phương chênh lệch giữa các giá trị trong mỗi nhóm với trung bình của chính nhóm (cột) đó.
Thay vào đó chúng ta vẫn sẽ tính SSG, tức tìm tổng các bình phương chênh lệch của trung bình nhóm (cột) so với trung bình chung. Ngoài ra tính thêm SSB, tổng các bình phương chênh lệch của trung bình khối (block, dòng) so với trung bình chung.
Công thức SSB, SSB phản ánh sự khác biệt doanh thu là do sự khác biệt giữa các cửa hàng:
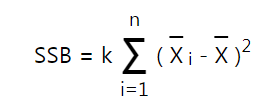
k là số cột, xi là trung bình theo dòng i, x là trung bình chung.
Công thức SSG, SSG phản ánh sự khác biệt doanh thu là do áp dụng các phương pháp khác nhau
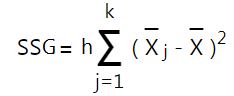
h là số dòng, sẽ bằng với số quan sát, ở đây có 6 cửa hàng. Nếu tập dữ liệu có block/ khối thì h là số block.
SSG = 6*(692.17 – 784.63)^2 +…. + 6*(966.33 – 784.63)^2 = 275120.8
SSB = 4*(722.5 – 784.63)^2 + …. + 4*(708.25 – 784.63)^2 = 227879.4
Các con số có thể sai lệch với kết quả của các bạn do số được làm tròn
Cách tính SST đơn giản hơn, chúng ta tính chênh lệch của từng giá trị trong bảng dữ liệu so với trung bình chung, rồi tính tổng.
SST = (572 – 784.63)^2 + … + (950 – 784.63)^2 = 663378.63
Bây giờ là công thức quan trọng cần phải nhớ:
SST = SSG + SSB + SSE
SSE phản ánh sự chênh lệch của các giá trị trong tập dữ liệu mà do yếu tố khác không đề cập trong nghiên cứu.
Vậy SSE khác với SSW như thế nào? Lấy ví dụ để nói cho dễ.
SSW phản ánh sự chênh lệch hay khác biệt trong doanh thu của các cửa hàng áp dụng chung phương pháp do yếu tố khác không đề cập trong nghiên cứu.
SSE bao gồm cả sự khác biệt trong doanh thu của các cửa hàng áp dụng chung phương pháp và sự khác biệt trong doanh thu của một cửa hàng khi áp dụng các phương pháp khác nhau đều do yếu tố khác không đề cập trong nghiên cứu. Nói cách khác, SSE phản ánh tất cả những sự chênh lệch, biến thiên của các đối tượng trong tập dữ liệu mà do yếu tố yếu tố khác không đề cập trong nghiên cứu. SSE có thể xem là mô tả tốt hơn SSW.
Trong Completely randomized design mà ở lần đầu tiên triển khai ANOVA, SSW đo lường sự khác biệt của 24 cửa hàng do yếu tố khác không đề cập trong nghiên cứu, còn SSE thực ra chỉ đo lường sự khác biệt của 6 cửa hàng mà thôi, cho dù ở mỗi phương pháp nào đi nữa.
Đến đây có thể cũng đủ để các bạn hiểu tại sao nên sử dụng Randomized block design trong thực tế nếu có khả năng.
Công thức khác của SSE
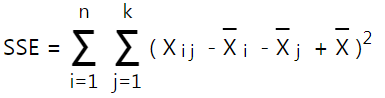
Chúng ta tính SSE = SST – SSG – SSB = 160377.46
- Tính phương sai
Tiếp theo chúng ta tính phương sai hay trung bình của các chênh lệch bình phương
MSG = SSG/ (k – 1)
MSG = 275120.8/ (4 – 1) = 91706.93
MSE = SSE/ (k – 1)*(h – 1)
MSE = 160377.46/ (4 – 1)*(6 – 1) = 10691.83
- Giá trị kiểm định F
Công thức tính giá trị kiểm định F:
F = MSG/ MSE
F = 91706.93/ 10691.8 = 8.57
F tra bảng với bậc tự do k – 1 (ở phần numerator trong bảng phân phối F) và (k – 1)(h – 1) ở (phần Denominator trong bảng phân phối F), mức ý nghĩa α ở đây là 0.05
- F tra bảng = 3.29
F > F tra bảng, vậy chúng ta bác bỏ H0. Kết luận có ít nhật một cặp phương pháp khác nhau về giá trị trung bình doanh thu tổng thể. Tổng quan thì các phương pháp công ty áp dụng có tác động lên doanh thu của 6 cửa hàng.
Cách phân tích sâu ANOVA, hay nói cách khác là tìm các cặp trung bình tổng thể để xác định sự khác biệt giữa 2 phương pháp bất kỳ trong tác động của nó lên doanh thu các cửa hàng, các bạn xem lại ở bài viết phần 1 nếu chưa biết về LSD, HSD. Dưới đây là công thức phân tích sâu ANOVA áp dụng cho Randomized block design với yếu tố tác động thứ nhất (k, cột)
LSD = t(k -1)(h – 1), α/2 * (MSE)1/2 * (2/ h)1/2
T (HSD) = qα, k, (k – 1)(h – 1) * (MSE/ h)1/2
Dưới đây là bảng ANOVA tóm tắt:

ANOVA – 2 yếu tố
Sau khi đã tìm hiểu cách phân tích ANOVA cho trường hợp Randomized design block, thì dạng đầu tiên của ANOVA 2 yếu tố sẽ rất dễ hiểu.
ANOVA – 2 yếu tố chia làm 2 dạng:
- Without replication, không lặp lại – chỉ thực hiện nghiên cứu trên một đơn vị quan sát, và không lặp lại nghiên cứu tương tự cho các quan sát khác, mỗi kết hợp giữa 2 yếu tố chỉ có 1 đơn vị quan sát đại diện được nghiên cứu. Xét ở khía cạnh bảng dữ liệu thì 1 ô sẽ chỉ chứa 1 giá trị của 1 đối tượng quan sát mà thôi.
- With replication, lặp lại – lặp lại thực hiện nghiên cứu trên nhiền đơn vị quan sát, mỗi kết hợp giữa 2 yếu tố có thể được đại diện bởi một mẫu gồm nhiều đơn vị quan sát. Xét ở khía cạnh bảng dữ liệu thì 1 ô sẽ chứa nhiều hơn 1 giá trị của các đối tượng quan sát. Và lúc này không chỉ kiểm tra sự tác động của mỗi yếu tố lên đối tượng nghiên cứu, mà chúng ta còn phải phân tích mối quan hệ tương tác của cả 2 yếu tố.
Dạng đầu tiên, ANOVA – 2 yếu tố “không lặp lại”, có cấu trúc bảng giống trường hợp chúng ta vừa làm tức thì. Để hiểu rõ hơn chúng ta cùng đi tiếp ví dụ:
Mặc dù sau khi đã triển khai ANOVA 1 yếu tố cho 2 trường hợp nghiên cứu (bằng cách chọn ngẫu nhiên 24 cửa hàng, 1 phương pháp sẽ lấy ngẫu nhiên 6 cửa hàng để thử nghiệm, và bằng cách chọn ngẫu nhiên 6 cửa hàng bất kỳ, mỗi cửa hàng sẽ được thử nghiệm hết 4 phương pháp), công ty vẫn muốn tìm hiểu thêm là liệu yếu tố vị trí có ảnh hưởng lên doanh thu trung bình của các cửa hàng không?
Quay trở lại với 6 cửa hàng được chọn ngẫu nhiên ở trên:
Giả sử 6 cửa hàng trên là 6 cửa hàng lớn nhất đại diện cho 6 thành phố khác nhau thuộc bang California:
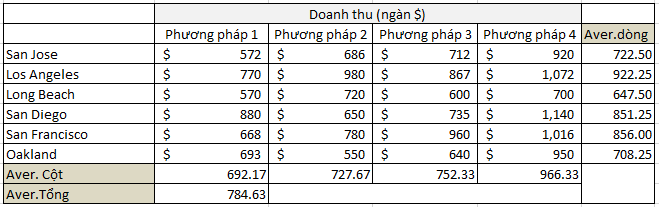
Đặt giả thuyết H0: µ1 = µ2 = µ3 = µ4
H1: ít nhất có 2 trung bình doanh thu tổng thể (phương pháp) khác nhau
Chúng ta làm tương tự như các bước ở trên và đến bước tính phương sai, chúng ta sẽ tính thêm MSB, phương sai giữa các khối:
MSB = SSB/ (h – 1)
MSB = 227879.4/ (6 – 1) = 45575.88
Tiếp theo tích tỷ số F, giá trị kiểm định cần tìm:
F = MSB/ MSE = 45575.88/ 10691.83 = 4.26
F tra bảng với bậc tự do (h – 1) = 5, ở phần numerator của bảng phân phối F, và (k – 1)*(h – 1) = (4 – 1)*(6 – 1) = 15, mức ý nghĩa α = 0.05 là 2.9
F > F tra bảng, vậy bác bỏ H0 kết luận yếu tố vị trí có tác động lên doanh thu, cụ thể là các cửa hàng ở các thành phố khác nhau sẽ có doanh thu khác nhau.
Đối với ANOVA 2 yếu tố, công thức phân tích sâu ANOVA cũng tương tự như trên:
Nếu so sánh theo yếu tố thứ nhất (k cột hay k nhóm) để so sánh các cặp phương pháp:
LSD = t(k -1)(h – 1), α/2 * (MSE)1/2 * (2/ h)1/2
T (HSD) = qα, k, (k – 1)(h – 1) * (MSE/ h)1/2
Nếu so sánh theo yếu tố thứ hai (h dòng hay h khối) để so sánh các cặp thành phố:
LSD = t(k -1)(h – 1), α/2 * (MSE)1/2 * (2/ k)1/2
T (HSD) = qα, h, (k – 1)(h – 1) * (MSE/ k)1/2
Thực chất nếu các bạn đảo lại bảng dữ liệu, thứ yếu tố thứ hai sẽ thành yếu tố thứ nhất, k cột sẽ là h dòng và ngược lại. Các bạn xem lại bài viết phần 1 để hiểu cách phân tích sâu ANOVA, do bài viết có giới hạn nen chúng tôi không trình bày lại.
Bảng ANOVA – 2 yếu tố dạng không lặp (without replication), các bạn thấy dưới đây có 2 tỷ số F khác với bảng ở trên chỉ có 1, và mỗi tỷ số F là giá trị kiểm định sự tác động của một yếu tố. Phương pháp ANOVA – 2 yếu tố thực chất cho phép chúng ta phân tích cùng lúc 2 yếu tố thay vì 1 yếu tố, mà trong thực tế dĩ nhiên khi nghiên cứu đến 1 đối tượng chúng ta quan tâm đến nhiều yếu tố tác động thay vì 1, và ANOVA 2 – yếu tố cho phép quá trình phân tích diễn ra nhanh hơn.
Lưu ý thêm: các bạn có thể tính p-value dựa trên giá trị kiểm định F, sử dụng bảng phân phối F và so sánh với 0.05, nếu thấp hơn thì bác bỏ H0 hoặc ngược lại.

Như vậy chúng ta đã tìm ANOVA – 2 yếu tố dạng thứ nhất khá đơn giản. Chúng ta cùng sang dạng thứ 2, ANOVA – 2 yếu tố có lặp (with replication)
Giả sử công ty mở rộng phạm vi nghiên cứu, muốn thử nghiệm nhiều hơn 1 cửa hàng tại 2 thành phố lớn nhất của bang California là Los Angeles, San Diego, cũng được coi là 2 thị trường trọng điểm. Mỗi kết hợp giữa thành phố và phương pháp công ty sẽ chọn ra 5 cửa hàng để thử nghiệm. Tuy nhiên sau các lần nghiên cứu thì thấy phương pháp 2, 3, 4 hiệu quả hơn phương pháp 1, nên lần này công ty sẽ bỏ phương pháp 1. Tổng cộng 3×2 = 6 kết hợp, mỗi kết hợp có 5 cửa hàng ngẫu nhiên, nên tổng cộng sẽ cần 30 cửa hàng, mỗi thành phố sẽ cần 15 cửa hàng đưa vào nghiên cứu. Doanh thu ghi nhận trong 1 tuần thử nghiệm
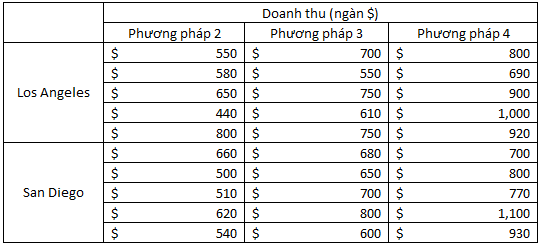
Bảng dữ liệu như sau:

Các bạn có thể thấy khác với các bảng trên, mỗi ô trong bảng này có nhiều hơn 1 quan sát, đây là dấu hiệu cho thấy cần áp dụng ANOVA 2 – yếu tố dạng replication.
Để dễ dàng quan sát và tính toàn chúng ta sẽ làm lại bảng số liệu:
Đầu tiên chúng ta sẽ đặt giả thuyết, ở đây sẽ có 3 giả thuyết H0 cần được đặt:
- Doanh thu trung bình của cửa hàng áp dụng các phương pháp khác nhau là như nhau, không có sự khác biệt. Hay yếu tố phương pháp không tác động lên doanh thu.
- Doanh thu trung bình của cửa hàng có vị trí tại các thành phố khác nhau là như nhau. Hay yếu tố thành phố không tác động lên doanh thu.
- Giữa yếu tố thành phố và yếu tố phương pháp không có mối tương tác với nhau. Nghĩa là, tác động của phương pháp lên doanh thu trung bình là như nhau đối với các cửa hàng nằm ở các thành phố khác nhau và tác động của thành phố lên doanh thu trung bình là như nhau đối với các cửa hàng áp dụng phương pháp khác nhau.
Chúng tôi sử dụng luôn ví dụ để trình bày cách tính, và không trình bày tóm tắt các công thức tránh làm quá dài bài viết, và để các bạn hiểu nhanh hơn.
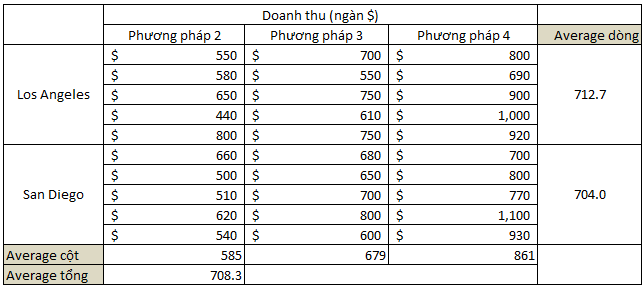
Chúng ta sẽ tính tung bình từng nhóm, tức từng cột cho yếu tố phương pháp, sau đó tính trung bình theo từng khối cho yếu tố thành phố, và tính trung bình chung toàn tập dữ liệu. Các bạn sẽ được kết quả như sau:
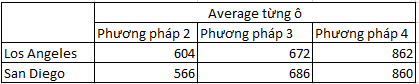
Tiếp theo chúng ta sẽ tính trung bình từng kết hợp
Tiếp theo chúng ta tính tổng chênh lệch các bình phương:
Lưu ý khác với các công thức ở trên, trong các công thức SSG, SSB các chênh lệch bình phương thường nhân với hệ số H và K. Còn ở trường hợp Replication, sẽ nhân thêm với L, là số quan sát trong 1 ô, hay 1 kết hợp, trong bảng số liệu đầu tiên, thì mỗ ô là 5, nên L = 5
Với H = 2, K = 3, L = 5. Các bạn lưu ý nhìn bảng số liệu đầu tiên của ví dụ này, để xác định số dòng H, số cột K, và số quan sát trong ô L.

Các kết quả có thể chênh lệch với các bạn do quy tắc làm tròn
(HxL) SSG = 2*5*(585– 708.3)^2 + …. + 2*5(861 – 708.3)^2 = 393786.7
(KxL) SSB = 3*5*(712.7 – 708.3)^2 + 3*5*(704 – 708.3)^2 = 563.33
SSI là tổng chênh lệch bình phương giữa các kết hợp (giao nhau giữa 2 yếu tố – Sum squares of interaction). SSI = L* (trung bình từng kết hợp – trung bình cột của yếu tố cột kết hợp – trung bình dòng của yếu tố khối kết hợp + trung bình chung)
Ví dụ SSI của Los Angeles và phương pháp 2:
- Trung bình kết hợp = 604
- Trung bình cột phương pháp 2 = 585
- Trung bình dòng Los Angeles = 712.7
- Trung bình chung = 708.3
SSILaxPP2 = 5*(604 – 585 – 712.7 + 708.3)^2 = 1075.5
Các bạn tính SSI cho các kết hợp còn lại
SSI tổng = 3546.7
SST = SSG + SSB + SSI + SSE
Chúng ta sẽ phải tìm SST, rồi mới có thể xác định được SSE
SST tính đơn giản hơn, nó là tổng chênh lệch bình phương của các giá trị trong tập dữ liệu với trung bình chung.
SST = (550 – 708.3)^2 + …. + (930 – 708.3)^2 = 699416.7
Suy ra SSE = SST – SSG – SSB – SSI = 301520
SSE phản ánh tất cả những sự chênh lệch, biến thiên của các đối tượng trong tập dữ liệu mà do yếu tố yếu tố khác không đề cập trong nghiên cứu.
Lần lượt tính các phương sai cho SSG, SSB, SSI, SSE với các bậc tự do (phần dưới mẫu số) tương ứng
MSG = SSG/ (K – 1) = 393786.7/ (3 – 1) = 196893.3
MSB = SSB/ (H – 1) = 563.33/ (2 – 1) = 563.33
MSI = SSI/ (K – 1)(H – 1) = 3546.7/ 2 = 1773.3
MSE = SSE/ K*H*(L – 1) = 301520/ (2*3*4) = 12563.3
Tiếp theo chúng ta sẽ tính từng tỷ lệ F để làm giá trị kiểm định cho 3 giả thuyết ở đầu bài:
- F1 = MSG/ MSE = 15.67
- F2 = MSB/ MSE = 0.044
- F3 = MSI/ MSE = 0.14
Chúng ta sẽ so sánh với từng giá trị F tra bảng
- F tra bảng với bậc tự do K – 1 = 2 ở phần numerator trong bảng phân phối F, và K*H*(L – 1) = 24, ở phần denominator, α = 0.05 là 3.40
F1 > F tra bảng. Vậy bác bỏ giả thuyết H0, tức yếu tố phương pháp có tác động lên doanh thu trung bình của các cửa hàng
- F tra bảng với bậc tự do H – 1 = 1, ở phần numerator trong bảng phân phối F, và K*H*(L – 1) = 24, ở phần denominator, α = 0.05 là 4.25
F2 < F tra bảng. Vậy không bác bỏ giả thuyết H0, tức doanh thu trung bình của các cửa hàng tại Los Angeles và San Diego là không có sự khác biệt.
- F tra bảng với bậc tự do (H – 1)(K – 1) = 2, ở phần numerator trong bảng phân phối F, và K*H*(L – 1) = 24, ở phần denominator, α = 0.05 là 3.40
F3 < F tra bảng. Vậy không bác bỏ giả thuyết H0, tức yếu tố phương pháp, và yếu tố thành phố không có sự tương tác với nhau trong việc ảnh hưởng lên doanh thu trung bình của các cửa hàng.
Chúng ta có bảng ANOVA tổng quát:
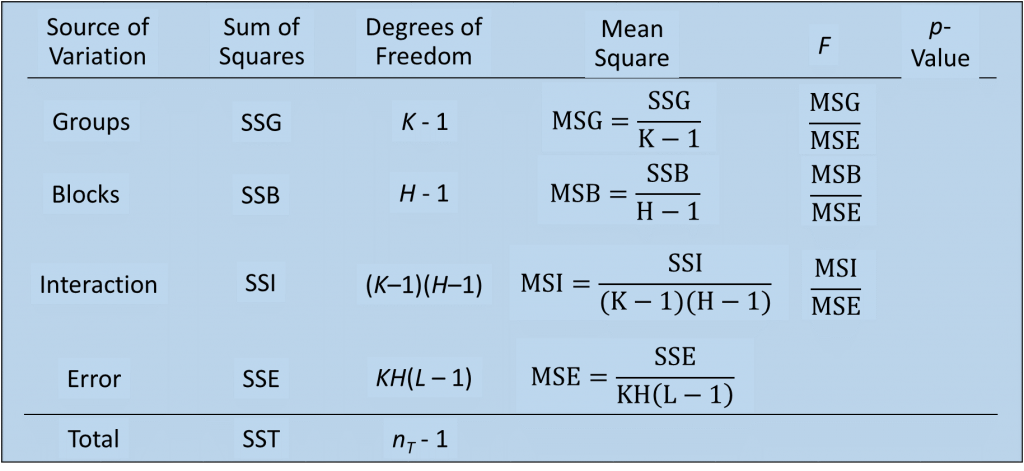
Kết quả từ excel

Công thức phân tích sâu ANOVA, HSD:
So sánh 2 nhóm (cột) trong yếu tố thứ nhất, ví dụ so sánh phương pháp 2 và 3
T = qα, K, KH(L – 1) * (MSE/ (H*L))1/2
So sánh 2 khối (dòng) trong yếu tố thứ hai ví dụ so sánh Los Angeles và San Diego
T = qα, H, KH(L – 1) * (MSE/ (K*L))1/2
Các bạn xem lại bài viết phần 1 để cách triển khai phân tích HSD, và thử so sánh các cặp phương pháp ở ví dụ trên.
Tài liệu tham khảo:
“Essentials of Statistics for The Behavioral Sciences” của các tác giả Frederick J Gravetter, Larry B. Wallnau, Lori-Ann B. Forzano
“Basic statistics for business and economics” của các tác giả Douglas A. Lind, William G. Marchal, Samuel A. Wathen
“Statistics for Business and Economics” của các tác giả David R. Anderson, Dennis J. Sweeney, Thomas A. Williams và cộng sự
Như vậy đến đây là kết thúc chủ đề về ANOVA. Mong qua 2 bài viết các bạn sẽ hiểu và vận dụng được các phân tích ANOVA cơ bản vào thực tế. Hẹn gặp lại các bạn ở những chủ đề khác.Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English