Trong các bài viết với những chủ đề khác nhau ở mục Blog, BigDataUni đã giới thiệu đến các bạn những lý thuyết thống kê, statistics cơ bản từ tóm tắt, thống kê dữ liệu, thống kê mô tả để tìm hiểu những đối tượng trong mẫu dữ liệu cho đến thống kê suy luận bao gồm các phương pháp ước lượng, kiểm định.để đưa ra các kết luận về tổng thể nghiên cứu, và đánh giá chúng. Đến với bài viết lần này BigDataUni sẽ tiếp tục giới thiệu đến các bạn một mảng kiến thức quan trọng khác trong thống kê, và được ứng dụng ở nhiều lĩnh vực khác nhau chính là phân tích phương sai hay còn gọi với tên viết tắt là ANOVA.
Phân tích phương sai ANOVA là “phiên bản nâng cấp” của kiểm định tham số đặc biệt là kiểm định 2 mẫu kiểm định sự khác biệt giữa 2 đối tượng nghiên cứu khi có hoặc không có một yếu tố tác động nào đó (2 mẫu độc lập), hoặc 1 đối tượng nghiên cứu trước và sau khi có một yếu tố tác động nào đó (2 mẫu phụ thuộc).
Do đó trong trường hợp chúng ta muốn phân tích sự khác biệt giữa nhiều đối tượng nghiên cứu khác nhau, muốn xem xét tác động của hai yếu tố lên các đối tượng nghiên cứu khác nhau thì cần cách tiếp cận khác ngoài phương pháp kiểm định thông thường và đó chính là ANOVA – Analysis of Variance
Những bạn nào chưa biết gì về thống kê cũng như kiểm định thì nên tham khảo trước ở những tài liệu khác hoặc qua các bài viết của chúng tôi ở các link dưới đây trước khi tìm hiểu nội dung về ANOVA trong bài viết này để dễ nắm bắt hơn:
Tổng quan về Statistics: Khái niệm và ứng dụng của thống kê
Tổng quan về Statistics: Descriptive statistics (thống kê mô tả)
Tổng quan về Statistics: Inferential statistics (thống kê suy luận)
Tìm hiểu về phương pháp kiểm định tham số
Các dạng kiểm định tham số (trường hợp 1 mẫu)
Các dạng kiểm định tham số (trường hợp 2 mẫu)
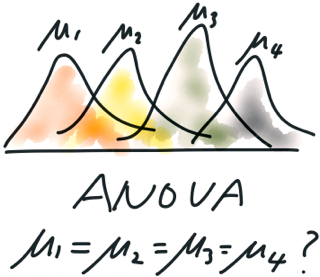
Các bạn có thể nhìn thấy hình minh họa trên mô tả động cơ của phương pháp phân tích phương sai chính là so sánh giá trị trung bình của các tổng thể, và khi các tham số tổng thể là chưa biết, chúng ta sẽ sử dụng các trung bình mẫu để so sánh, kết hợp với phương pháp kiểm định giả thuyết, để đưa ra các kết luận sau cùng về các tổng thể. Cũng vì lý do này mà nhiều người thường gọi đây là kiểm định ANOVA. Tuy nhiên nếu gọi là kiểm định thì ANOVA lại mang khuynh hướng của Hypothesis test thông thường nhưng thực chất không phải như vậy. Cách thức vận hành của ANOVA là hoàn toàn khác biệt!
Nếu kiểm định thông thường sử dụng những tham số mẫu, chuyển đổi thành giá trị chuẩn hóa Z để xác định giá trị kiểm định thì ANOVA sử dụng các chênh lệch bình phương của những trung bình mẫu từ các tổng thể để tính toán phương sai, rồi giá trị kiểm định sau cùng. Chi tiết công thức chúng tôi sẽ trình bày ở các phần sau từ đó các bạn sẽ hiểu vì sao phương pháp này có tên gọi rất đẹp là ANOVA.
Để minh họa rõ hơn về ANOVA chúng ta cùng tìm hiểu qua một ví dụ thực tế trong lĩnh vực kinh doanh:
Một công ty thực phẩm sản xuất mỳ gói muốn tìm hiểu chi tiết về mỗi yếu tố tác động lên quyết định mua sản phẩm của người tiêu dùng ngoại trừ độ nổi tiếng thương hiệu, chỉ tập trung vào các đặc tính sản phẩm, cơ bản có 5 yếu tố chính:
- Hương vị chính (vị lẩu thái, bò hầm, rau củ hầm chay, cay vị Hàn Quốc,…)
- Chất liệu mỳ, loại mỳ
- Cách thức đóng gói (mỳ đóng gói, đóng hộp cầu kỳ)
- Hình ảnh bên ngoài bao bì
- Khối lượng tịnh
- Giá bán
Với mỗi các yếu tố, công ty sẽ phân ra thành nhiều nhóm hay nhiều loại sản phẩm, tiến hành phân tích và kiểm tra sự khác biệt trong doanh thu trung bình.
Ví dụ: Hương vị, công ty sẽ so sánh sự khác biệt trong doanh thu trung bình giữa mỳ có hương vị lẩu thái, hương vị bò hầm, hay hải sản cay Hàn Quốc. Mẫu dữ liệu của mỗi loại sẽ có kích cỡ là n = 100, 100 ngày ghi nhận doanh thu cho mỗi loại lấy ngẫu nhiên từ dữ liệu giao dịch lịch sử qua các năm. Chúng ta sẽ sử dụng ANOVA – 1 yếu tố hay còn gọi one-way/ one-factor ANOVA. Nếu doanh thu trung bình 100 ngày của 3 loại mỳ này là khác nhau, thì kết luận Hương vị có tác động lên quyết định mua hàng của người tiêu dùng.
Tuy nhiên công ty nhận thấy rằng cần xét thêm các yếu tố khác nữa khi xu hướng cho thấy khách hàng ưa chuộng đóng hộp hơn, khối lượng nhiều hơn và giá rẻ hơn, vậy thì sẽ phải kết hợp với yếu tố Hương vị để đưa ra đánh giá chính xác hoặc xem giữa cách thức đóng gói, hình ảnh, khối lượng, giá có cái nào tương tác hay cộng hưởng với yếu tố Hương vị tác động lên quyết định mua hàng của khách hàng hay không. Lúc này chúng ta sẽ cần đến ANOVA – 2 yếu tố, two-way/ two-factor ANOVA.
Nếu sử dụng phương pháp kiểm định thông thường, thì có lẽ “sẽ rất lâu” để công ty hoàn thành công trình nghiên cứu của mình. Ví dụ đơn giản Hypothesis test thông thường cao nhất chỉ có thể kiểm định sự khác biệt giữa 2 mẫu mà thôi như vậy chỉ có thể so sánh giữa 2 loại mỳ khác nhau, số lần so sánh sẽ là 3 lần, không kể kết hợp thêm yếu tố khác.
Các điều kiện để thực hiện phân tích phương sai hay còn gọi là những giả định ban đầu của bài toán:
- Ở mỗi tổng thể nghiên cứu, những giá trị của các biến mục tiêu hay biến phụ thuộc hay đối tượng nghiên cứu chúng ta quan tâm phải có phân phối chuẩn (normal distribution).
- Phương sai, ký hiệu σ2 , phải bằng nhau ở tất cả các tổng thể σ12 = σ22 = σ32 = …. = σk2 với k là số tổng thể nghiên cứu
- Các mẫu dữ liệu được lấy ra từ các tổng thể nghiên cứu một cách ngẫu nhiên.
- Các quan sát bên trong mẫu phải độc lập với nhau
Ở 2 điều kiện ban đầu nếu dữ liệu không đáp ứng được yêu cầu thì chúng ta phải sử dụng đến phương pháp phân tích ANOVA kết hợp kiểm định phi tham số áp dụng với dữ liệu định tính sau khi đã được chuyển đổi từ dữ liệu định lượng ban đầu. Chúng tôi sẽ trình bày cụ thể phần này cùng với các cách kiểm tra 2 điều kiện kể trên ở bài viết về “Các dạng kiểm định phi tham số” sắp tới. Còn trong bài viết lần này chúng ta sẽ tìm hiểu ANOVA cho dữ liệu định lượng và tạm giả định các ví dụ tuân theo phân phối chuẩn và có cùng phương sai.
Tóm tắt tổng quan về các dạng phân tích ANOVA:
- ANOVA áp dụng cho dữ liệu phân phối chuẩn, phương sai bằng nhau và ANOVA áp dụng cho dữ liệu không theo phân phối chuẩn, phương sai không bằng nhau
- ANOVA áp dụng cho dữ liệu nghiên cứu có 1 yếu tố, và ANOVA áp dụng cho dữ liệu nghiên cứu có 2 yếu tố
- ANOVA áp dụng cho nghiên cứu thực nghiệm (Experimental Study) – các yếu tố tác động được kiểm soát, và dữ liệu thu thập với mục đích so sánh tác động của chúng trên lên đối tượng nghiên cứu. ANOVA áp dụng cho nghiên cứu quan sát (Observational Study), các yếu tố không được kiểm soát chặt chẽ.
Trong bài viết phần 1 chúng ta sẽ làm quen trước với ANOVA 1 yếu tố, sử dụng ví dụ trong lĩnh vực kinh tế.
One-way ANOVA/ ANOVA 1 yếu tố
Phân tích ANOVA 1 yếu tố là phân tích tác động của 1 yếu tố nguyên nhân nào đó lên một yếu tố kết quả đang quan tâm.
Bài toán ANOVA cũng giống bài toán kiểm định là chúng ta phải đưa ra ra giả thuyết ban đầu. Mục tiêu của ANOVA là so sánh các trung bình của tổng thể có khác biệt hay không nên chúng ta sẽ đặt giả thuyết như sau:
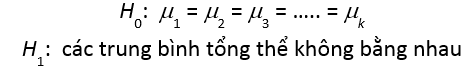
Nêu chấp nhận H0 chúng ta kết luận các trung bình tổng thể là giống nhau, còn nếu bác bỏ H0 thì kết luận ít nhất một cặp trung bình tổng thể có giá trị khác nhau.
Đồ thị phân phối của các trung bình mẫu x khi H0 đúng:
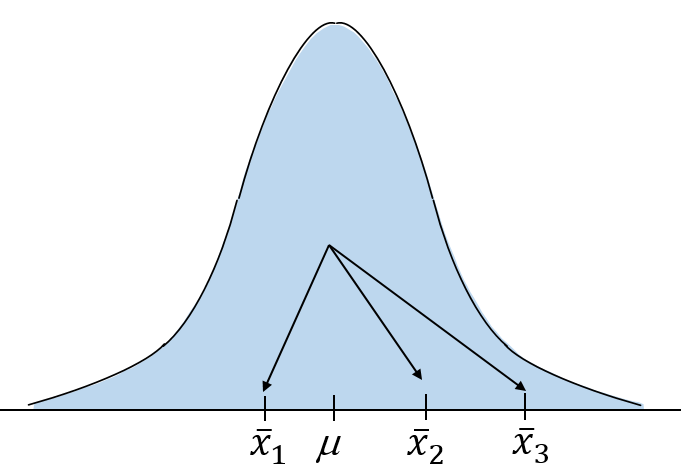
Các trung bình mẫu sẽ nằm gần nhau và trên cùng 1 đồ thị phân phối duy nhất
Đồ thị phân phối của các trung bình mẫu khi bác bỏ H0:
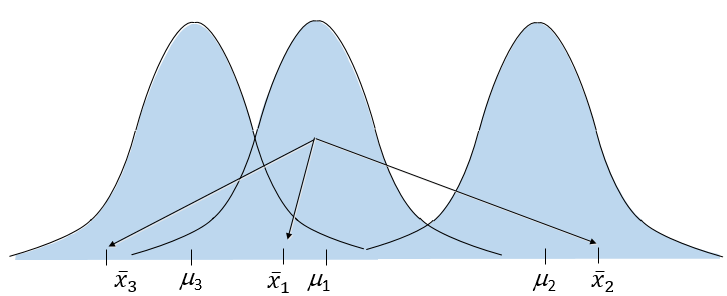
Các trung bình mẫu sẽ nằm xa nhau, ở 3 đồ thị phân phối, cho thấy sự khác nhau của 3 tổng thể.
Khác với các cuốn sách, giáo trình thống kê dạy về lý thuyết ANOVA thường nói công thức trước và ví dụ sau, ở bài này BigDataUni sẽ trình bày tóm tắt công thức vào đi vào ví dụ cụ thể để các bạn hiểu được bản chất một cách nhanh hơn thay vì vòng vo phần công thức, không cần phải hiểu quá kỹ về nguyên lý hoạt động của ANOVA, một phần cũng giúp các bạn nào đã học qua ANOVA review lại kiến thức trong thời gian ngắn.
- Đặt giả thuyết:
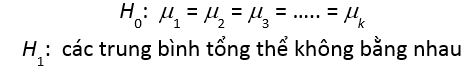
- Tính trung bình của từng nhóm
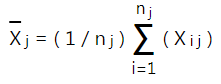
- Tính trung bình của tất cả các nhóm (trung bình chung toàn tập dữ liệu)
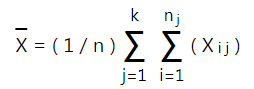
- Tính tổng các bình phương chênh lệch giữa các giá trị trong mỗi nhóm với trung bình của chính nhóm đó
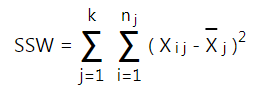
- Tính tổng các bình phương chênh lệch của trung bình nhóm so với trung bình chung ở bước 2:
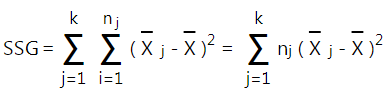
- Tính tổng chênh lệch bình phương của các giá trị trong tập dữ liệu so với trung bình chung ở bước 2:
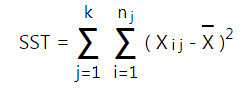
Ngoài ra: SST = SSG + SSW
- Tính phương sai, hay tính trung bình của các chênh lệch bình phương tìm được
MSW = SSW/ (n – k)
MSG = SSG/ (k – 1)
- Tính giá trị kiểm định F
F = MSG/ MSW
Bác bỏ H0, tức các trung bình tổng thể không bằng nhau, kết luận yếu tố tác động có ảnh hưởng lên đối tượng nghiên cứu khi:
F > Fk – 1, n – k, α
Ví dụ:
Một công ty bán lẻ toàn cầu có hơn 2000 cửa hàng phân bổ ở gần tất cả các bang trên nước Mỹ, vừa phát triển 4 phương pháp hay còn gọi là mô hình trưng bày hàng hóa, bán hàng, và cung cấp dịch vụ tại các cửa hàng.
- Phương pháp 1: thay đổi cách trưng bày hàng hóa thông thường hay truyền thống theo hướng hiện đại (ứng dụng phân tích dữ liệu)
- Phương pháp 2: thay đổi cách thức hỗ trợ khách hàng, ân cần, thân thiết hơn với phong cách phục vụ chuyên nghiệp
- Phương pháp 3: thay đổi thiết kế toàn bộ không gian hàng hóa, cải thiện môi trường không khí bên trong cửa hàng.
- Phương pháp 4: tích hợp robot hỗ trợ bán hàng bên cạnh thay đổi thiết kế gian hàng, cách trưng bày hàng hóa để tối đa thu hút khách hàng.
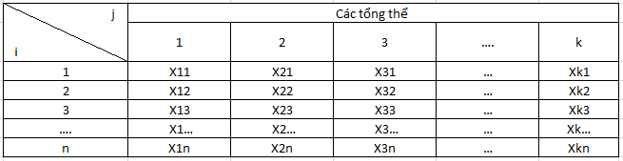
Một chuyên gia kinh tế cho rằng, người dân Mỹ mua hàng khi họ có nhu cầu và không thường quan tâm đến cửa hàng ra sao, dịch vụ như thế nào. Tuy nhiên chứng minh ngược lại ý kiến ấy, bộ phận chiến lược đã sáng tạo và thử nghiệm 4 phương pháp trên ở những cửa hàng khác nhau. Để đảm bảo loại bỏ yếu tố về nguồn cầu, nhân khẩu học. Công ty chọn tiểu bang đông dân nhất của nước Mỹ, California, cũng là nơi có nhiều cửa hàng nhất để chọn ra một số cửa hàng ngẫu nhiên. Mỗi phương pháp sẽ chọn ngẫu nhiên 6 cửa hàng để áp dụng, doanh thu tháng đầu tiên của mỗi cửa hàng sẽ được ghi lại. Bảng dữ liệu có được như sau, đơn vị 1000$:
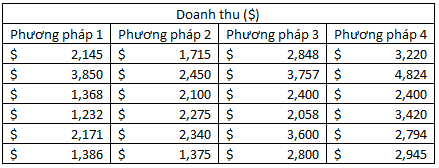
Đầu tiên đặt giả thuyết:
Gọi µ1, µ2, µ3, µ4 lần lượt là doanh thu trung bình của các cửa hàng ứng với phương pháp 1 đến 4. Giả thuyết H0 cho rằng doanh thu trung bình của các cửa hàng là bằng nhau, tức việc thay đổi phương pháp
H0: µ1 = µ2 = µ3 = µ4
H1: ít nhất có 2 trung bình doanh thu tổng thể khác nhau.
Giả sử các tổng thể tuân theo phân phối chuẩn và phương sai bằng nhau.
Bước 1:
Chúng ta tính trung bình doanh thu cho mỗi nhóm. Các bạn lưu ý ở mỗi giá trị X đều có dấu gạch chân trên đầu để phân biệt với giá trị thông thường trong tập dữ liệu và theo nguyên tắc nhận biết đây là trung bình của mẫu.
(Do format của web bị lỗi nên bị mất dấu gạch ngang ở trên mong các bạn thông cảm)
Ví dụ X1 = (2145 + 3850 + 1368 + 1232 + 2171 + 1386)/6 = 2025.3
Các bạn tính tương tự cho phương pháp 2, 3, 4.
Sau đó tính tổng trung bình doanh thu của tất cả cửa hàng, sử dụng giá trị trung bình của X1, X2, X3, X4 kết quả như sau:
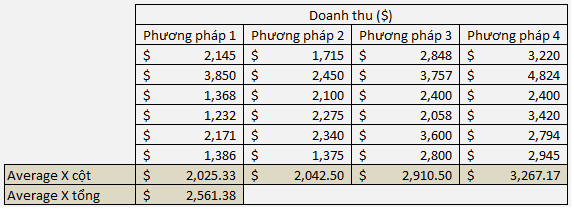
Bước 2:
Chúng ta tính tổng các chênh lệch bình phương ở các phương pháp.
Đầu tiên ở mỗi nhóm, chúng ta tính chênh lệch từng giá trị doanh thu so với trung bình của nhóm, sau đó tính tổng.
SS1 = (2145 – 2025.3)2 + (3850 – 2025.3)2 + … + (1368 – 2025.3)2 = 4835159.3
Các bạn tính tương tự SS2, SS3, SS4 . Kết quả như sau:

Tiếp theo chúng ta sẽ tính tổng tất cả các chênh lệch bình phương của các nhóm:
SSW = SS1 + SS2 + SS3 + SS4 = 11424321
SSW là tổng chênh lệch bình phương Sum of Squares Within-groups, tức bên trong từng nhóm. Nếu các SS lớn, dẫn đến SSW lớn thì cho thấy sự khác biệt trong doanh thu của các cửa hàng trong mỗi nhóm là do nguyên nhân, yếu tố khác không phải do các phương pháp mà công ty áp dụng. Và tác động của những yếu tố khác này lên doanh thu các cửa hàng trong cùng một nhóm là khá nghiêm trọng và cần tìm hiểu.
Ví dụ trong số các cửa hàng áp dụng phương pháp 1, sự chênh lệch trong doanh thu giữa cửa hàng có doanh thu thấp nhất và cao nhất là rất lớn, lý do có thể độ hiệu quả của các hoạt động marketing và sales quá khác biệt, mô hình kinh doanh của công ty chưa tốt khi các cửa hàng có thể chưa đồng bộ với nhau về quy trình vận hành. Tuy nhiên vẫn còn đó các yếu tố khách quan khác mà chưa được xét đến ví dụ đối thủ cạnh tranh, chuỗi cung ứng của đối tác,…
Tính tổng các chênh lệch bình phương giữa các nhóm Sum of squares Between groups (SSG)
Ở đây chúng ta sẽ tính tổng chênh lệch bình phương giữa trung bình mẫu của mỗi phương pháp với trung bình chung (của 4 phương pháp) nhân với số quan sát trong mẫu tại mỗi phương pháp.
SSG = 6*(2025.3 – 2561.38)^2 + 6*(2042.5 – 2561.38)^2 + 6*(2910.5 – 2561.38)^2 + 6*(3267.17 – 2561.38)^2 = 7059162.5 xấp xỉ 7060000
SSG là chỉ số khá quan trọng nếu chỉ số này lớn cho thấy giữa các nhóm có thể có sự khác biệt lớn, và sự khác biệt này là do sự khác nhau giữa các phương pháp 1, 2, 3, 4 hay nói cách khác yếu tố đang được nghiên cứu, là thứ tác động lên sự khác biệt trong doanh thu của các cửa hàng.
Sau cùng ở bước này chúng ta tính tổng chênh lệch bình phương toàn bộ tập dữ liệu:
SST = SSG + SSW = 18483933
Cách tính khác: tính tổng chênh lệch bình phương của tất cả các giá trị, các doanh thu hay các quan sát với trung bình chung toàn bộ (bằng 2561.38).
Theo công thức đầu tiên, ANOVA cho thấy sự khác biệt trong doanh thu của 2 cửa hàng bất kỳ có thể là do: yếu tố chính – là các phương pháp công ty áp dụng, và các yếu tố khác không được đề cập đến.
Nếu SSW lớn hơn rất nhiều so với SSG, thì công ty khả năng không chứng minh được các phương pháp mà mình áp dụng hay thay đổi cho các cửa hàng không đem lại sự khác biệt, doanh thu các cửa hàng khác nhau là do yếu tố khác gây ra, và ngược lại.
Tiếp theo là các bước tính giá trị kiểm định F.
Bước 3:
Tính phương sai, hay tính trung bình của các chênh lệch bình phương tìm được bằng cách lấy tổng các chênh lệch bình phương ở bước 2 chia cho bậc tự do tương ứng.
Phương sai trong nội bộ nhóm sẽ bằng cách lấy tổng chênh lệch bình phương nội bộ nhóm SSW chia cho bậc tự do n – k, với n là tổng số quan sát trong dữ liệu ở đây là 24, k là số nhóm so sánh ở đây là 4. MSW là ước lượng phương sai của các giá trị trong tập dữ liệu do yếu tố khác không được nghiên cứu, hay không được đề cập.
MSW = SSW/ (n – k) = 11424231/ (24 – 4) = 571216
Tiếp theo chúng ta tính phương sai giữa các nhóm bằng cách lấy tổng các chênh lệch giữa các nhóm là SSG chia cho bậc tự do k – 1. MSG là ước lượng phương sai của các giá trị trong tập dữ liệu do yếu tố nghiên cứu chính.
MSG = SSG/ (k – 1) = 7059612/ (4 – 1) = 2353204
Bước 4:
Giá trị kiểm định F:
F = MSG/ MSW = 2353204/ 571276 = 4.119
Nguyên tắc bác bỏ H0: F > F tra bảng với bậc tự do k – 1 ở phần Numerator (dòng trên cùng của bảng phân phối F) và n – k ở phần Denominator (cột ngoài cùng của bảng phân phối), và mức ý nghĩa α, lấy ví dụ ở đây là 0.05, kiểm định 1 phía
F tra bảng = 3.098
F > F tra bảng, F nằm trong vùng bác bỏ. Vậy bác bỏ H0 tức là ít nhất có 1 cặp trung bình của tổng thể là khác nhau.
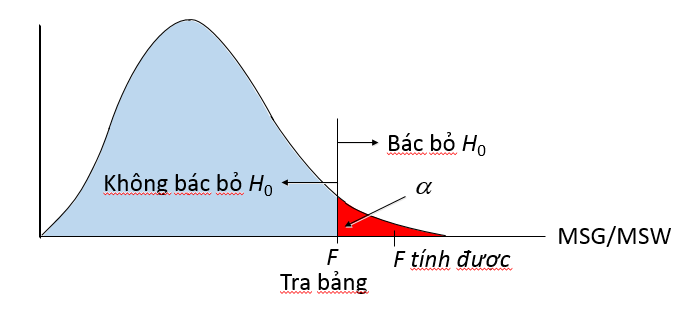
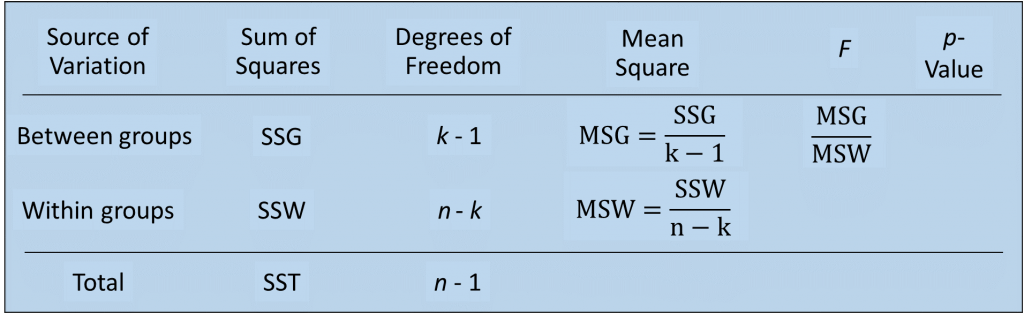
Bên trên là bảng tóm tắt ANONA, đây là bảng kết quả tiêu chuẩn thường được thể hiện trong các kết quả phân tích ở những phần mềm thống kê hay Data mining. Các bạn thử ghép lại các giá trị ở trên! Ngoài sử dụng F chúng ta có thể sử dụng P-value suy ra từ chính giá trị kiểm định F, ở đây P-value = 0.019 < 0.05 tức nằm trong phần diện tích màu đỏ ở trên đồ thị, kết luận bác bỏ H0 là hợp lý.
Thực chất thể hiện bài toán để các bạn hiểu được cách vận hành của ANOVA nhưng trong thực tế khi tập dữ liệu có nhiều quan sát thì việc tính toán sẽ phức tạp hơn. Lúc này các phần mềm thống kê như Minitab, SPSS,… sẽ hỗ trợ đắc lực, còn nếu bạn không có các phần mềm thống kê thì vẫn có thể sử dụng Excel. Đây là kết quả ví dụ ở trên:

Kết quả của Excel hoàn toàn trùng khớp với những gì BigDataUni và các bạn vừa tính ở trên.
Các phương pháp khác nhau sẽ tác động làm thay đổi doanh thu trung bình của các cửa hàng. Trong 4 phương pháp thì phương pháp thứ tư có khả năng mang lại doanh thu trung bình cao hơn so với các phương pháp còn, có thể do công nghệ robot bán hàng mang lại trải nghiệm khách hàng cao thu hút nhiều khách hàng. Mặt khác, các cửa hàng áp dụng phương pháp thứ nhất, chỉ thay đổi cách trưng bày hàng hóa thì chưa thực sự tác động mạnh hơn vào quyết định mua hàng của khách hàng so với trước đây, hơn nữa cho thấy sự chênh lệch rất lớn về doanh thu so với các cửa hàng dùng phương pháp thứ 4.
Theo như kết luận bác bỏ H0 ít nhất có 1 cặp trung bình của tổng thể là khác nhau. Công việc tiếp theo của công ty là tìm ra giữa 2 cửa hàng nào doanh thu sẽ khác biệt, so sánh sự hơn kém, để đưa ra đánh giá sau cùng cho các phương pháp mà công ty đề xuất.
Phân tích sâu ANOVA 1 yếu tố
Trước tiên chúng ta xác định có bao nhiêu cặp phương pháp cần so sánh. Sử dụng công thức tổ hợp để tìm, ở đây có 4 phương pháp, tổ hợp chập 2 của 4 sẽ là 6, tức có 6 cặp.
PP1 vs PP2, PP1 vs PP3, PP1 vs PP4, PP2 vs PP3, PP2 vs PP4, PP3 vs PP4
Có 2 phương pháp:
- Sử dụng Turkey, hay phương pháp HSD – Honestly Significant Differences
- Sử dụng phương pháp Fisher, LSD – Least significant difference
Chúng tôi lấy ví dụ vừa nói ở trên, so sánh các cửa hàng áp dụng phương pháp thứ 1 và các cửa hàng áp dụng phương pháp thứ 4
Đặt giả thuyết: H0: µ1 = µ4
H1: µ1 ≠ µ4
Giả thuyết H0 phát biểu doanh thu trung bình của các cửa hàng áp dụng PP1 sẽ bằng các cửa hàng áp dụng PP4.
Giá trị Turkey được tính theo công thức:
T = tα, k, n-k * (MSW/ ni)1/2
t là giá trị tra bảng Turley với mức ý nghĩa α, với bậc tự do k và n – k. MSW tìm được ở trên, ni là số quan sát trong 1 nhóm, nếu 2 nhóm có số quan sát khác nhau thì sẽ lấy cái nhỏ nhất. Ở đây số cửa hàng áp dụng PP1 và PP4 là bằng nhau và bằng 6
T = t0.05, 4, 24 – 4 * (571276/6)1/2 = 3.958*(571216/6)1/2 = 1221.23
Bảng phân phối Turkey có tên gọi khác là Studentized range distribution các bạn có thể search google để tìm.
Tiếp theo chúng ta sẽ tính giá trị tuyệt đối của chênh lệch trung bình 2 mẫu
X1 = 2025.33 và X4 = 3267.17
X4 – X1 = 3267.17 – 2025.33 = 1241.84 > T = 1221.23
Vậy trung bình X4 > X2 suy ra µ4 > µ1. Phương pháp số 4 giúp công ty tăng nhiều doanh thu hơn so với phương pháp số 1.
Còn theo công thức Fisher LSD:
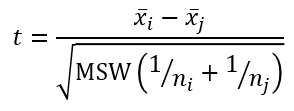
Sử dụng MSE để tính.
Giả thuyết đặt tương tự như trên:
t = (3267.17 – 2025.33)/ (571216*(2/6))1/2 = 2.845
Cơ sở bác bỏ H0 khi t > ta/2 với bậc tự do n – k, với n là tổng số quan sát. Với n – k =24 – 4 = 20, t tra bảng = 2.086
t > t tra bảng nên chúng ta sẽ bác bỏ H0
Cách khác: tính giá trị LSD và so sánh giống như Turkey
Công thức:
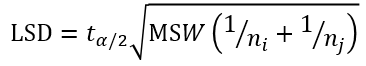
LSD = 2.086*(571216*(2/6))1/2 = 910
X4 – X1 = 3267.17 – 2025.33 = 1241.84 > LSD = 910. Vậy bác bỏ H0, kết luận tương tự như trên.
Như vậy đến đây kết thúc phần 1 bài viết về ANOVA. Sang phần 2 chúng ta sẽ đi vào ANOVA 2 yếu tố. Mong các bạn tiếp tục ủng hộ BigDataUni.
Tài liệu tham khảo:
“Essentials of Statistics for The Behavioral Sciences” của các tác giả Frederick J Gravetter, Larry B. Wallnau, Lori-Ann B. Forzano
“Basic statistics for business and economics” của các tác giả Douglas A. Lind, William G. Marchal, Samuel A. Wathen
“Statistics for Business and Economics” của các tác giả David R. Anderson, Dennis J. Sweeney, Thomas A. Williams và cộng sự
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English