Quay trở lại với chủ đề về phương pháp phân tích sống sót “Survival analysis”, ở bài viết trước chúng ta đã tìm hiểu về khái niệm, ứng dụng và đặc điểm dữ liệu được đưa sử dụng, tiếp tục phần 2 về Survival analysis, BigDataUni sẽ giới thiệu đến các bạn các lý thuyết về 2 function quan trọng trong nghiên cứu dữ liệu survival – được coi là động cơ vận hành của Survival analysis.
Các bạn nào chưa xem qua phần 1, nếu muốn có thể tham khảo bài viết qua link dưới đây:
Tìm hiểu về Survival analysis (P.1)

Trước khi đi vào phần trọng tâm của bài viết, chúng ta cùng tìm hiểu thuật ngữ và ký hiệu toán học thường sử dụng trong Survival analysis.
Các chuyên gia thường ký hiệu T cho một biến bất kỳ mô tả thời gian sống sót (hay khoảng thời gian cho đến khi xảy ra sự kiện) của người, của một đối tượng, là biến định lượng liên tục
Ví dụ T ký hiệu cho:
- Thời gian sống sót của bệnh nhân ung thư từ lúc được chẩn đoán cho đến khi tử vong
- Thời gian khách hàng đăng ký dịch vụ hay mua hàng của công ty cho đến khi rời bỏ
- Thời gian máy móc hoạt động bình thường sau khi đưa vào sử dụng cho đến khi bị hỏng hóc, hư hại cần thay mới
- Thời gian sau khi xét nghiệm lần đầu cho đến khi bị nhiễm virus

T gọi là biến số ngẫu nhiên do nó thể hiện giá trị cho một người hay một đối tượng được chọn bất kỳ, ngẫu nhiên từ tổng thể nghiên cứu. T mang giá trị dương, lớn hơn hoặc bằng 0, không mang giá trị âm
T = survival time (T có các giá trị ≥ 0)
Ngoài T, chúng ta ký hiệu t thể hiện giá trị cho một khoảng thời gian bất kỳ. Ví dụ chúng ta muốn biết một bệnh nhân ung thư có thể sống nhiều hơn 3 năm sau khi tiếp nhận liệu pháp điều trị hay không thì t = 3, chúng ta sẽ xem đối tượng nào có thời gian sống sót lớn hơn 3 năm không, hay giá trị T > t = 3.
Hoặc ngược lại, chúng ta muốn tìm hiểu một bệnh nhân ung thư giai đoạn cuối thường sẽ tử vong vào thời điểm nào trong giai đoạn 5 năm kể từ khi tiếp nhận điều trị. t = 5 và chúng ta sẽ xem đối tượng có thời gian sống sót nhỏ hơn 5 năm không hay giá trị T < t = 5
Ngoài T và t, các chuyên gia còn sử dụng ký hiệu d, không viết hoa thể thiện trạng thái của sự kiện quan tâm đã diễn ra hay chưa. d cũng được coi là biến ngẫu nhiên, khi nó xem xét trạng thái sự kiện xảy ra hoặc chưa xảy ra đối với một người hoặc đối tượng được chọn ngẫu nhiên từ tổng thể nghiên cứu.
d có 2 giá trị:
- d = 0 nếu sự kiện chưa xảy ra trong thời gian nghiên cứu, trường hợp này cũng được coi là censoring, khi chúng ta không biết sau khi bỏ theo dõi đối tượng, sự kiện có xảy ra đối với họ hay không. Nghĩa thứ hai, tức là sự kiện đã không xảy ra trong thời gian nghiên cứu. Nghĩa thứ ba, đối tượng rời khỏi hay bị loại bỏ khỏi nghiên cứu.
- d = 1 nếu sự kiện quan tâm đã xảy ra trong thời gian nghiên cứu và được ghi nhận cụ thể.
Tiếp tục chúng ta đi qua các function, hay hiểu đơn giản là động cơ vận hành của các phương pháp trong Survival analysis, các function này còn có tên gọi là Life-time function.
Survival Function
Đầu tiên đối với biến ngẫu nhiên T đã nói ở trên, theo lý thuyết thống kê, chúng ta sẽ có hàm độ lớn hay mật độ xác suất f(t) và hàm phân phối xác suất tích lũy F(t).
Phần kiến thức này là kiến thức cơ bản trong thống kê, bạn nào chưa biết thì nên xem lại ở các giáo trình thống kê đã học, chúng tôi chỉ tóm tắt lại điểm khác biệt, qua 1 ví dụ đơn giản
Giả sử cho rằng khách hàng sẽ phản hồi và lần phản hồi đó có thể xảy ra vào 1 trong 6 tháng, tức tháng 1, hoặc tháng 2, 3, … 6 ngẫu nhiên và độc lập.
Xác suất để sự kiện xảy ra trong mỗi tháng là như nhau, đây là trường hợp hàm độ lớn hay mật độ xác suất f(t)

Tiếp theo giả sử thay vì cung cấp dữ kiện lần phản hồi đó có thể xảy ra vào 1 trong 6 tháng,… chúng ta nói chắc chắn trong 6 tháng, khách hàng sẽ phản hồi. Vậy xác suất khách hàng phản hồi sẽ tăng dần từ tháng 1, đến tháng 6.

Ví dụ do khẳng định trong 6 tháng khách hàng sẽ phản hồi ít nhất 1 lần, nên nếu tháng 1, 2 không phản hồi, thì khả năng tháng 3, 4, 5 phản hồi sẽ tăng dần, hoặc nếu không, thì khả năng phản hồi trong tháng 6 sẽ cao nhất là 6/6 = 1 tức 100%.
F(x) = sum (f(x), X ≤ x ) = P (X ≤ x)
Mối quan hệ giữa f(x) và F(x) còn theo công thức toán học như sau:

Quay trở lại với survival analysis, như vậy nếu chúng ta coi quá trình nghiên cứu diễn ra một cách liên tục, f(t) sẽ là hàm mật độ xác suất cho sự kiện xảy ra vào một thời điểm bất kỳ trong khoảng thời gian nghiên cứu t. Gọi khoảng thời gian từ lúc bắt đầu nghiên cứu đến thời điểm đó là T.
Vì T nằm trong (0; t), nên áp dụng hàm phân phối tích lũy chúng ta có công thức:
F(t) = P (T≤ t)
Thể hiện xác suất xảy ra sự kiện trong khoảng thời gian (0; t) hay xác suât để T thuộc (0; t). Phân phối tích lũy được tính bằng công thức tích phân như trên
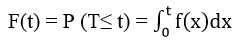
Tiếp tục trong Survival analysis, cái chúng ta quan tâm là thời gian đến lúc sự kiện xảy ra tức, trong khoảng thời gian này sự kiện sẽ không xảy ra.
Như vậy xác suất để sự kiện không xảy ra (đồng nghĩa với “sống sót”) trong khoảng thời gian nghiên cứu (0; t) ký hiệu S(t) (còn được gọi là Survivor Function), T nằm ngoài (0; t) tức T > t:
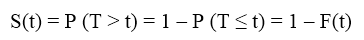
Ví dụ, chúng ta muốn tìm hiểu xác suất khách hàng sẽ không phản hồi trong 6 tháng:
S(t) = P (T > 6) = 1 – P (T ≤ 6).
Nếu khách hàng chắc chắn phản hồi trong 6 tháng thì S(t) = 1 – 1 = 0
Gọi là Survivor function vì nó tích lũy xác suất sống sót của đối tượng nghiên cứu (không xảy ra sự kiện) ở các t khác nhau, qua đó mang lại nhiều thông tin quan trọng cho Survival analysis.
Do t là một số tự nhiên từ 0 đến ∞ và khi S(0) = 1, S(∞) = 0. Xác suất tích lũy giảm dần khi thời gian tăng. Ví dụ, thời gian tăng khì tuổi thọ con người giảm, tỷ lệ sống sót sẽ giảm dần. Đồ thị biểu diễn Survival function như sau:
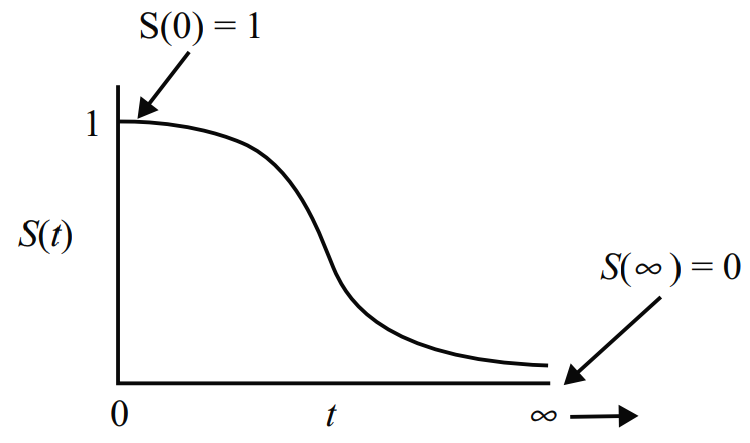
Giải thích lại, tại S(0) = 1, tức chưa bắt đầu nghiên cứu, nên ở trạng thái hiện tại, các đối tượng quan sát đều chưa gặp sự kiện xảy ra, nên xác suất sống sót sẽ bằng 1
Còn t tiến tới vô cực, nghĩa là nếu nghiên cứu diễn ra trong thời gian vô thời hạn, thì khả năng sống sót hay khả năng để sự kiện không xảy ra sẽ bằng 0. Nghĩa là sự kiện chắc chắn sẽ xảy ra.
Lý do xác suất tích lũy giảm khi t tăng còn được hiểu theo công thức f(t) suy ra từ S(t)
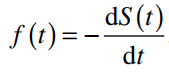
Để hiểu các công thức, các bạn cần xem lại các kiến thức toán phổ thông đạo hàm, tích phân và vi phân.
Hazard Function
Bên cạnh quan tâm đến khả năng sống sót của đối tượng hay khả năng sự kiện không xảy ra, thì trong Survival analysis chúng ta còn quan tâm đến tỷ lệ tại một thời điểm mà ở đó sự kiện sẽ xảy ra, sử dụng Hazard function – “động cơ vận hành” chính của Survival analysis.
Hazard function, hàm Hazard, hàm rủi ro còn được gọi là hàm cường độ, nó tính khả năng mà một đối tượng nghiên cứu (người, sự vật,…) trải qua một sự kiện (đồng nghĩa với “thất bại, “hỏng hóc”, “tử vong) được quan tâm trong một khoản thời gian theo dõi với điều kiện đối tượng này chưa trải qua sự kiện đó cho đến thời điểm bắt đầu theo dõi.
Ví dụ trong quá trình 1 tháng theo dõi bệnh nhân Covid-19, các bệnh nhân tiếp nhận điều trị có thể sống sót hay cầm cự qua 2 tuần, từ tuần thứ 2 đến tuần thứ 4 nếu bệnh trở nặng, khả năng tử vong rất cao. Để tìm hiểu liệu tuyên bố trên có chính xác, các chuyên gia y tế kiểm tra tỷ lệ tử vong từ tuần thứ 2 đến thứ 4 của các bệnh nhân Covid-19 còn sống. Hazard function lúc này sẽ được sử dụng.
Hiểu đơn giản, giả sử một đối tượng chưa trải qua một sự kiện đang được quan tâm ở thời điểm t, và chúng ta muốn biết sau t một khoảng thời gian Δt nào đó, xác suất xảy ra sự kiện đó là bao nhiêu, chúng ta sẽ dùng đến Hazard. Trong y học, hàm Hazard được dùng để tìm hiểu một người sống sót tại thời điểm t, và liệu các thời điểm sau t, người đó còn sống sót hay không.
Hàm Hazard còn được gọi là tỷ lệ sự kiện xảy ra có điều kiện, và tỷ lệ này được tính liên tục theo suốt khoảng thời gian theo dõi, và điều kiện là ở thời điểm bắt đầu, sự kiện phải chưa xảy ra (T ≥ t)
Hazard được dịch là “rủi ro” được sử dụng để tính “nguy cơ” một sự kiện được quan tâm sẽ xảy ra ví dụ nguy cơ bệnh nhân tử vong, nguy cơ khách hàng rời dịch vụ,…
Tỷ lệ hazard hay tỷ lệ rủi ro được hiểu là tỷ lệ giữa số đối tượng trải qua sự kiện (ví dụ số bệnh nhân đã tử vong, số khách hàng đã rời dịch vụ,…) trong khoảng thời gian theo dõi bắt đầu ở thời điểm t, chia cho tích của số đối tượng chưa trải qua sự kiện (ví dụ số bệnh nhân chưa tử vong, số khách hàng chưa rời dịch vụ,…)tại thời điểm t, và tính trên đơn vị thời gian
Công thức đầy đủ của hàm Hazard
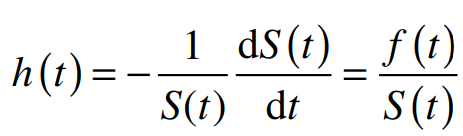
Điểm thú vị khác giữa Survival function và Hazard function khi nhìn qua 2 công thức, đó là có thể dựa trên kết quả của một hàm bất kỳ để suy ra kết quả hàm còn lại.
Hoặc:
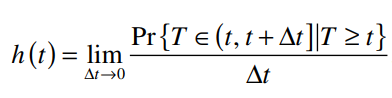
Tỷ lệ rủi ro tính từ hàm Hazard là tỷ lệ giới hạn có điều kiện. Lý do được giải thích như sau. Biết Δt = t1 – t0 hay giữa thời điểm t bắt đầu theo dõi cho đến thời điểm kết thúc theo dõi chúng ta có khoảng thời gian bằng Δt.
Ở Survival function, chúng tôi có nhắc đến khi thời gian nghiên cứu càng kéo dài (t tiến đến ∞) thì tỷ lệ sống sót, tỷ lệ không xảy ra sự kiện càng giảm (xác suất sống sót tiến đến 0), ngược lại tỷ lệ xảy ra sự kiện, tỷ lệ “chết” càng tăng.
Vì tỷ lệ Hazard được tính liên tục theo thời gian, từ t (thời điểm bắt đầu) đến t + Δt (thời điểm kết thúc), khoảng thời gian Δt càng lớn (cho đến thời điểm kết thúc), t + Δt càng lớn, tỷ lệ Hazard sẽ càng tăng. Qua đó kết quả phân tích có thể không chính xác.
Để hạn chế kết quả bị “biased” do Δt tăng theo thời gian, các chuyên gia thêm phần mẫu số Δt vào công thức để tính tỷ lệ Hazard/ 1 đơn vị thời gian (giới hạn lại Δt). Hoặc nói cách khác, thay vì tính tỷ lệ trên một khoảng thời gian dài, chúng ta sẽ sử dụng các khoảng thời gian ngắn hơn, được giới hạn lại cho đến 1 đơn vị thời gian. Ví dụ, thay vì tính tỷ lệ rủi ro chung giữa ngày 1 và ngày 30 trong tháng, chúng ta tính từ ngày 1, đến ngày 2, và từ ngày 2 tính cho ngày 3,..
Ngoài ra, Δt = t1 – t0. t0 ở đây còn được hiểu là thời điểm trước đó. Khi thời gian nghiên cứu kéo dài, mà chúng ta xem xét tỷ lệ Hazard trong ngắn hạn, tức ở từng đơn vị thời gian, thì t0 sẽ càng tiến gần t1, Δt càng nhỏ dần. Và nếu chúng ta tính tỷ lệ Hazard tại một thời điểm, đơn vị thời gian cụ thể (như đơn vị tuần, ngày, giờ), t0 = t1, Δt tiến đến 0. Cách hiểu khác, đó là tỷ lệ hazard là tỷ lệ rủi ro có điều kiện trong khoảng thời gian được giới hạn dần về 0.
Từ đó, các tỷ lệ Hazard được tính theo giới hạn lim Δt tiến đến 0. Cách giải thích khá phức tạp, có phần khó hiểu nhưng rất cần thiết cho các bạn, hiểu rõ về Hazard function giúp bạn nắm bắt tốt hơn các phương pháp phân tích được chúng tôi đề cập sắp tới.
Tính liên tục ở đây được hiểu như sau. Ví dụ bạn chạy xe máy với vận tốc 50km/ giờ, dự báo trong 2 tiếng bạn sẽ đến nơi, sau 1 tiếng bạn quan sát đồng hồ tốc độ chỉ 45 km/ giờ, như vậy nếu bạn giữ nguyên tốc độ này, thì trong 1 tiếng tới bạn sẽ chạy được 45 km. Tuy nhiên, bởi vì bạn có thể làm chậm hoặc tăng tốc độ hoặc thậm chí ngừng trong giờ tiếp theo, 45 km/ giờ sẽ không cho bạn biết quãng đường bạn thực sự sẽ đi trong 1 tiếng tiếp theo. Đồng hồ tốc độ chỉ cho bạn biết bạn đang đi nhanh như thế nào tại một thời điểm nhất định; nghĩa là, cho bạn biết vận tốc tức thời.
Tương tự như vậy, hàm rủi ro hazard h(t) cung cấp tỷ lệ rủi ro tức thời tại thời điểm t để chỉ ra nguy cơ xảy ra một sự kiện, chẳng hạn như tử vong. Tỷ lệ rủi ro tại thời điểm t cho thấy trước đó, sự kiện chưa xảy ra, chẳng hạn bệnh nhân đã sống sót ra sao cho đến thời điểm t, như vận tốc 45 km/h chứng minh rằng bạn đã đi một quảng đường dài trong 1 tiếng trước đó.
Dưới đây là đồ thị minh họa
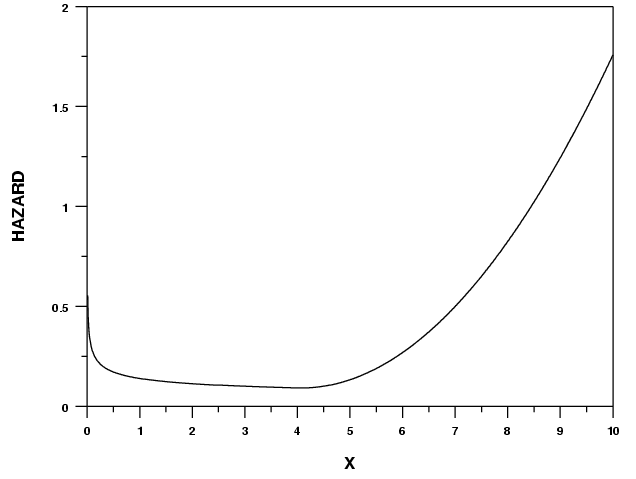
Lưu ý tỷ lệ Hazard chưa hẳn xác suất ở một số trường hợp, mặc dù tử số là công thức xác suất có điều kiện, nhưng khi chia cho mẫu Δt, có thể có giá trị sau cùng > 1 khi Δt thay đổi.
Khác với đồ thị mô tả Survival function, đường cong đi xuống, tiến đến 0 khi thời gian tăng, ngược lại ở Hazard, đường cong sẽ đi lên như đã nói, thời gian tăng, nguy cơ xảy ra sự kiện ngày càng cao.
- Khi khả năng xảy ra sự kiện là bằng 0, tỷ lệ hazard cũng sẽ thấp nhất.
- Nếu nguy cơ sự kiện xảy ra tăng lên theo thời gian, tỷ lệ hazard cũng sẽ tăng theo, tín hiệu không tốt trong tương lai
- Nếu nguy cơ sự kiện xảy ra giảm dần theo thời gian, tỷ lệ hazard cũng sẽ giảm dần, tương lai có thể tươi sáng hơn
Dấu chấm thứ 3 chỉ là mơ ước của các bác sĩ đối với bệnh nhân của mình sẽ sống sót qua thời gian, là mơ ước của những công ty đối với những khách hàng sẽ thể hiện lòng trung thành với công ty trong suốt vòng đời của họ, trong thực tế thì rất hiếm khi nào xảy ra, và nếu hiếm như vậy, Hazard function hay Survival analysis cũng không cần dùng đến. Dấu chấm thứ 2 là phổ biến nhất, nó gần giống như cái gì đó gọi là quy luật tự nhiên.
Ví dụ, khách hàng không thể mãi mua hàng của một công ty, họ có thể chọn lựa công ty khác, thương hiệu khác, mà các bạn cũng biết, ở thị trường nào, lĩnh vực kinh doanh nào đều đang cạnh tranh rất khốc liệt. Còn về sức khỏe, ngày càng xuất hiện nhiều căn bệnh lạ, những căn bệnh mới như Covid-19, và thậm chí các căn bệnh cũ có những biến chứng mới nguy hiểm hơn, tác động lên tuổi thọ trung bình của mỗi người, và dĩ nhiên không ai là bất tử.
Thế nhưng nếu nói không có cách nào cải thiện hay giảm tỷ lệ rủi ro là hoàn toàn sai! Và đây là mục đích của Survival analysis và các chuyên gia hướng đến. Ví dụ trong y học, chắc chắn nếu không có liệu pháp điều trị thì người bệnh ung thư theo thời gian có tỷ lệ tử vong rất cao, nhưng nếu dự báo được nguy cơ tử vong ở thời điểm nào trong tương lai và tiến hành áp dụng các liệu pháp phù hợp thì tỷ lệ tử vong theo thời gian sẽ giảm, tùy theo tình hình bệnh.
Trong kinh doanh, khi biết được khả năng khách hàng bỏ công ty sau bao nhiêu lâu gắn bó, các nhà marketing và sales sẽ dĩ nhiên tìm giải pháp giữ chân khách hàng như các chương trình khuyến mãi, giảm giá,… và tỷ lệ khách hàng rời dịch vụ sẽ giảm theo thời gian.
Quay trở lại với đồ thị, tỷ lệ rủi ro, hay tỷ lệ Hazard có thể chạy từ 0 (chắc chắn sự kiện không xảy ra, nguy cơ thấp nhất) đến vô cực (sự kiện chắc chắn xảy ra ngay tại thời điểm xét, nguy cơ cao nhất). Như giải thích ở trên, theo thời gian, tỷ lệ rủi ro có thể tăng, giảm, không đổi hoặc thậm chí có nhiều hình dạng ngoằn ngoèo. Ví dụ tỷ lệ sai sót của dây chuyền sản xuất 2/ ngày, tức trong nguyên 1 ngày, có thể sai sót tới 2 lần, tỷ lệ này có thể tăng, giảm hoặc giữ nguyên cho ngày sắp tới. Nếu tỷ lệ giữ nguyên trong ngày, thì khả năng cứ đến nửa ngày, dây chuyền sẽ mắc lỗi.
Ở phía trên chúng tôi có in nghiêng lưu ý là tỷ lệ Hazard không phải xác suất và có thể lớn hơn 1, để làm rõ điều này, các bạn cùng xem ví dụ sau:
Ví dụ theo công thức Hazard, giả sử xác suất sống sót P ở trên tử số tính được là 1/5, khoảng thời gian theo dõi là 1/2 ngày, tức nửa ngày, vậy tỷ lệ là (1/5)/(1/2) = 0.4/ ngày. Giả sử thay vì tính trên đơn vị ngày, chúng ta đổi sang tuần 1/2 ngày, tương ứng 1/14 tuần. tỷ lệ lúc này (1/5)/ (1/14) = 2.8/ tuần. > 1. Nên nói tỷ lệ Hazard chưa hẳn là xác suất có điều kiện là khá hợp lý.
Ngoài hàm Hazard cơ bản, như trình bày ở trên, chúng ta còn 1 loại hàm rủi ro quan trọng khác, đó là hàm Hazard tích lũy (Cumulative Hazard function) do bài viết có giới hạn nên chúng tôi không thể trình bày quá sâu ở đây.
Hàm Hazard tích lũy có nguyên lý hoạt động gần giống xác suất tích lũy mà chúng tôi nói đến ở đầu bài viết. Hàm Hazard tích lũy được hiểu là tính tổng các tỷ lệ rủi ro trong một khoảng thời gian nào đó. Ví dụ tỷ lệ tử vong của một người là 100/ ngày, vậy trong 2 ngày tới, tỷ lệ tử vong tổng sẽ là 200, trong 3 ngày tới sẽ là 300.
Trong thực tế sẽ có người làm phân tích quan tâm đến việc liệu từ hàm Hazard có giúp họ tìm được gì từ hàm Survival, như hàm mật độ xác suất, phân phối xác suất tích lũy, và tỷ lệ sống sót.
Hàm rủi ro tích lũy tính tổng tỷ lệ rủi ro tích lũy đến thời điểm t nào đó đang được xét đến, công thức tổng quan như sau:
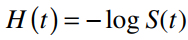
Hay:
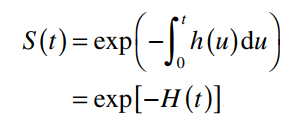
Các bạn phân biệt ký hiệu hàm rủi ro tích lũy và hàm rủi ro thông thường thông qua chữ H in hoa và H thường. Một số công thức khác thể hiện mối quan hệ giữa H(t), F(t), f(t)
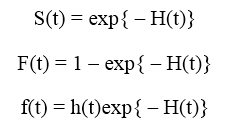
Ví dụ, một loại máy móc sản xuất có tỷ lệ rủi ro mắc lỗi 2/ ngày, và biết rằng tỷ lệ này được giữ nguyên đến cuối ngày, tỷ lệ rủi ro được tích lũy, tức chúng ta có H(t) = 2/ ngày. Xác suất để không xảy ra lỗi S(t) = exp (-2) = 0.135. Tỷ lệ để mắc ít nhất 1 lỗi F(t) = 1 – exp(-2) = 0.86.
Đến đây như vậy, chúng tôi đã giải thích khá kỹ về 2 function rất quan trọng trong Survival analysis. Chúng tôi khuyến khích các bạn đọc thêm tài liệu khác về 2 function này, đây sẽ là cơ sở để các bạn tìm hiểu kỹ hơn về Survival analysis.
Một số quy luật phân phối quan trọng trong Survival analysis (phần tham khảo thêm)
Chúng ta đã tìm hiểu về tỷ lệ sống sót, tỷ lệ rủi ro thông qua 2 hàm Survival và Hazard. Tiếp tục phần tiếp theo, chúng ta sẽ đi qua một số quy luật phân phối xác suất quan trọng trong Survival analysis.
Trong tự nhiên chúng ta sẽ có nhiều tổng thể nghiên cứu có tính chất, đặc điểm khác nhau, do đó các đối tượng khác nhau ở các tổng thể khác nhau khả năng sẽ có tỷ lệ sống sót/ tử vong khác nhau theo thời gian nói cách khác sẽ có T khác nhau (thời gian đến khi sự kiện xảy ra). Từ đó hình thành các quy luật phân phối nhất định theo thời gian.
Hàm Hazard và Survival áp dụng cho các tập dữ liệu có phân phối khác nhau có thể có đồ thị trực quan khác nhau. Do đó, có thể tìm thấy quy luật phân phối nhanh bằng cách đọc đồ thị
Đối với quá trình Survival analysis áp dụng phương pháp phân tích định lượng (chúng tôi sẽ nói ở phần 4), việc xác định quy luật phân phối để giả định cho dữ liệu cũng rất cần thiết.
Do bài viết có hạn nên chúng tôi chỉ giới thiệu 5 quy luật phân phối thường thấy trong Survival analysis. Ngoài ra, đây là phần để các bạn tham khảo thêm, trong các bài viết sắp tới, ở các ví dụ cụ thể chúng tôi sẽ không đề cập lại tất cả các quy luật, mà chỉ đi vào cái quy luật chính nào mà dữ liệu mẫu có.
- Normal distribution: phân phối chuẩn
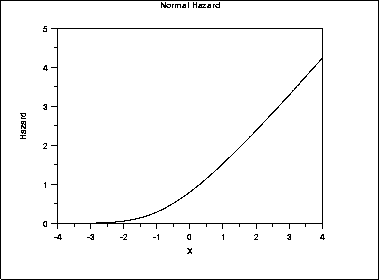
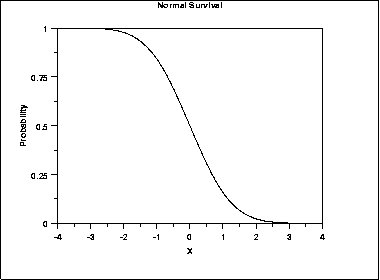
Tỷ lệ rủi ro có tốc độ tăng mạnh theo thời gian, tăng đột ngột. Và tỷ lệ sống sót giảm với tốc độ chậm hơn và có tính đơn điệu, đường cong sống sót có dạng như đồ thị dưới đây
- Uniform distribution: phân phối đều
Đây là dạng hiếm gặp trong thực tế, khi đường cong sống sót từ thể hiện tỷ lệ sống sót 100% xuống 0% là một đường thẳng. Còn tỷ lệ rủi ro sẽ tăng theo cấp số nhân để “ép buộc” các đối tượng phải trải qua sự kiện (ví dụ tử vong) ở thời điểm kết thúc nghiên cứu
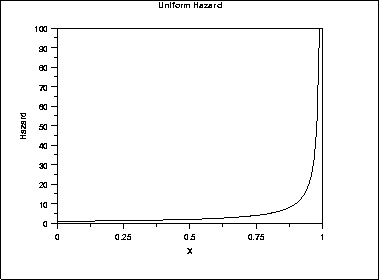
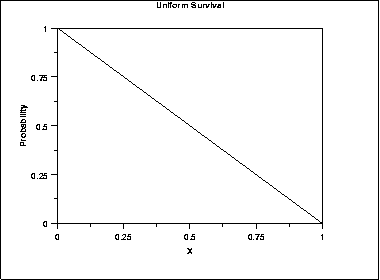
- Exponential Distribution: phân phối mũ
Tỷ lệ rủi ro hay Hazard giữ nguyên theo thời gian, và xác suất sống sót giảm theo thời gian có đồ thị giống đồ thị hàm mũ.
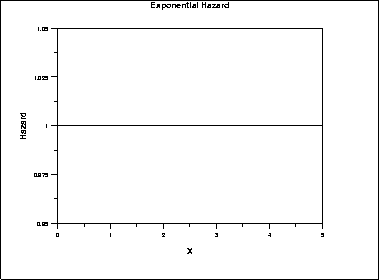
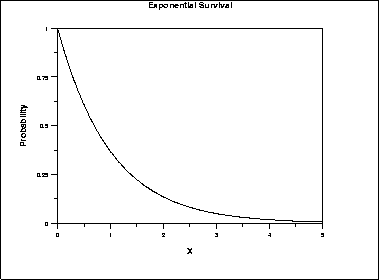
- Weibull Distribution: phân phối Weibull
Quy luật phân phối có áp dụng hệ số, thường được gọi là hệ số gamma, hệ số này sẽ được tối ưu để xác định các quy luật phân phối khác nhau cho tỷ lệ rủi ro, và tỷ lệ sống sót
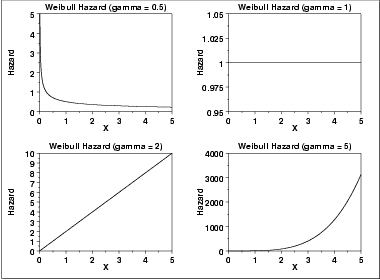
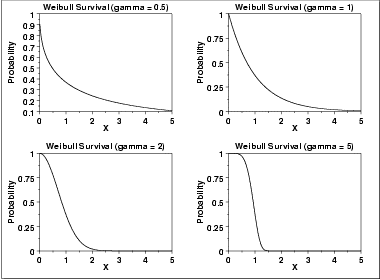
Như bạn có thể thấy từ nhiều tình huống, gamma có thể thay đổi tỷ lệ nguy cơ suy giảm từ với tốc độ nhanh thành giữ nguyên không đổi hoặc tăng nhanh. Do đó, nó phù hợp với nhiều tình huống trong thế giới thực của chúng ta.
- Log-normal distribution
Hoạt động tương tự như Weibull nhưng khác công thức và dùng hệ số sigma.
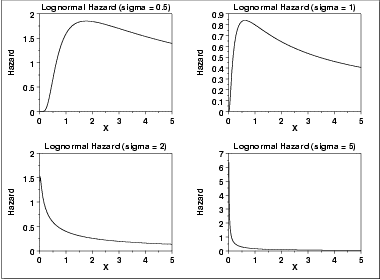
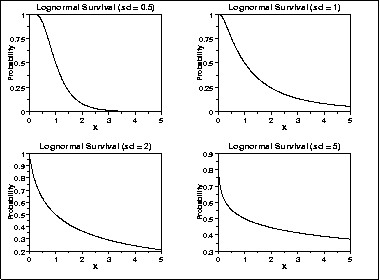
Như bạn có thể nhận thấy từ các đồ thị trên với sự thay đổi giá trị của sigma, các quy luật phân phối sẽ thay đổi theo hình dạng khác nhau.
Để xác định chính xác các quy luật phân phối, phương pháp phân tích định lượng phù hợp, chúng ta phải biết cách trực quan, mô tả dữ liệu trong survival analysis để khám phá, tìm hiểu Survivor function hay Hazard function của các đối tượng nghiên cứu thông qua các công thức ước lượng – những cái này còn được gọi là phương pháp phi tham số.
Bài viết phần 3 tới chúng ta sẽ tìm hiểu chi tiết.
Tài liệu tham khảo:
https://www.itl.nist.gov/div898/handbook/eda/section3/eda3661.htm
https://towardsdatascience.com/survival-analysis-part-a-70213df21c2e
https://towardsdatascience.com/survival-analysis-intuition-implementation-in-python-504fde4fcf8e
http://www.sthda.com/english/wiki/survival-analysis-basics
https://www.kdnuggets.com/2017/11/survival-analysis-business-analytics.html
“An Introduction to Survival Analysis” – Mario Cleves và cộng sự
“Survival Analysis A Practical Approach” – David Machin và cộng sự
“Survival Analysis – Models and Applications” – Xian Liu và cộng sự
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English