Quay trở lại với chủ đề phân tích sống sót Survival analysis, ở bài viết phần 1 và phần 2 chúng ta đã tìm hiểu khái niệm và ứng dụng, cũng như hai hàm quan trọng nhất của phương pháp này đó là Survival Function (hàm sống sót) và Hazard Function (hàm rủi ro). Tiếp tục với phần 3 Survival analysis, BigDataUni và các bạn sẽ cùng đi qua những phương pháp phi tham số trong mô tả, phân tích, ước lượng tỷ lệ sống sót, rủi ro, hay tỷ lệ xảy ra sự kiện được quan tâm đối với từng đối tượng trong tổng thể nghiên cứu.
Dành cho những bạn chưa tham khảo các bài viết trước:
Tìm hiểu Survival analysis (P.1): Khái niệm, ứng dụng
Tìm hiểu Survival analysis (P.2): Survival và Hazard Function

Parametric vs Non – parametric
Trước khi đi vào các phương pháp phi tham số trong Survival analysis, các bạn cần hiểu trước phi tham số là gì và khác biệt giữa nó với tham số.
Trong các phương pháp phân tích trong Statistics hay Data mining, chúng được chia làm 2 loại chính là phi tham số (Non-parametric) và tham số (Parametric). Giải thích đơn giản sự khác biệt giữa chúng.
Phi tham số không có nghĩa là nó không hề có tham số nào cả, cái tên gọi dễ khiến chúng ta hiểu nhầm. Các phương pháp phi tham số cũng không vì thế mà được cho là đơn giản hơn so với những phương pháp tham số, khi nguồn dữ liệu đưa vào khai thác càng lớn thì độ khó và tính phức tạp của chúng cũng sẽ tăng theo.
Trong mô hình phân tích phi tham số, vẫn có tham số, nhưng số lượng tham số sẽ không thể xác định một cách đầy đủ, vì khả năng nó là vô số. Ngược lại trong mô hình tham số, chúng ta luôn xác định được một nhóm những tham số cố định, cấu tạo nên cấu trúc, hình hài của mô hình, hỗ trợ phân tích tác động của các yếu tố khác lên đối tượng nghiên cứu (các tham số thường đại diện cho các yếu tố).
Linear regression, Multi-linear regression, logistic regression là các mô hình tiêu biểu cho phương pháp tham số mà chúng ta đã được biết đến. Mỗi mô hình đều có một biến phụ thuộc (biến mục tiêu) và các biến độc lập (biến dự báo) đóng vai trò là những tham số được xác định từ đầu. Còn K- láng giềng gần nhất (K-nearest neighbor) hay thuật toán cây quyết định (Decision trees) chỉ có 1 biến mục tiêu duy nhất lúc đầu, các yếu tố, các tham số sẽ dần được lộ diện nhiều hơn khi càng nhiều dữ liệu được đưa vào mô hình.
Cũng chính vì thế, phương pháp phi tham số được sử dụng phổ biến trong Survival analysis giai đoạn tìm hiểu dữ liệu, nhất là khi nguồn dữ liệu có khối lượng lớn và việc tìm ra các tham số để xây dựng mô hình phân tích, dự báo ngay lập tức là vô cùng khó khăn. Phương pháp phi tham số mặc dù yêu cầu nguồn dữ liệu lớn nhưng nó giúp chúng ta giảm bớt đi gánh nặng là phải tìm chính xác các thuộc tính cần có cho đối tượng nghiên cứu.
Việc xác định trước các tham số cũng khiến cho Parametric models kém hiệu quả hơn so với Non-parametric models khi kết quả phân tích, kết quả dự báo chúng mang lại có thể thiếu chính xác do nó bỏ sót những tham số hay yếu tố khác chưa khám phá đến, lý do có thể từ chính cách thức xây dựng mô hình hoặc nguồn dữ liệu bị giới hạn. Còn non-parametric models sẽ cho chúng ta thấy mô hình mô tả toàn diện về đối tượng nghiên cứu khi chỉ cần “nạp” cho chúng nguồn dữ liệu dồi dào.
Cách phân biệt khác, trong thống kê thường nói đến, đó là xác định quy luật phân phối xác suất (Probability Distribution). Khi áp dụng các mô hình tham số cho mẫu dữ liệu bất kỳ, chúng ta phải giả định dữ liệu đang tuân theo một quy luật phân phối xác suất nào đó (ví dụ phân phối chuẩn, phân phối chi bình phương, Poisson,…), và quy luật này có thể được giả định dựa trên một nhóm các tham số quen thuộc như trung bình (Mean), trung vị (Median), phương sai (Variance) hoặc độ lệch chuẩn (Standard deviation). Ngược lại trường hợp phi tham số chúng ta sẽ không phải đi tìm quy luật phân phối xác suất, không cần phải đưa ra giả định gì về các quy luật. Và vì thế, Non-parametric models còn được gọi là Distribution – free/ Assumption – free models.
Mỗi phương pháp đều có ưu điểm và khuyết điểm, chúng ta cần xem xét kỹ bối cảnh phân tích, nguồn dữ liệu cho phép, nhu cầu, năng lực phân tích để lựa chọn phù hợp.
Ưu điểm của các mô hình tham số nằm ở điểm là chúng đơn giản, dễ hiểu, dễ nắm bắt kết quả phân tích, tốc độ phân tích cũng nhanh hơn, cho phép tìm hiểu về đối tượng nghiên cứu nhanh hơn, không yêu cầu nhiều dữ liệu cho quá trình training mô hình. Tuy nhiên khuyết điểm có thể khiến người làm phân tích chủ quan, cho rằng mô hình mình làm ra có thể trả lời tất cả các câu hỏi về đối tượng nghiên cứu nhưng thực chất không phải như vậy. Parametric models phù hợp tìm lời giải cho các vấn đề đơn giản, không phức tạp vì “năng lực khai phá” của nó đã bị giới hạn ngay từ lúc ấn định các tham số, và tiến hành xây dựng mô hình riêng biệt, đặc thù.
Ưu điểm của phi tham số chính là sự linh hoạt, có thể cho chúng ta nhiều mô hình khác nhau mà không phụ thuộc vào số lượng các tham số ban đầu, không bị ràng buộc bởi chính các giả định chúng ta đưa ra, khắc phục các khuyết điểm của mô hình tham số trong dự báo, hiệu quả mang lại cao hơn. Tuy nhiên, đòi hỏi chúng ta phải có nguồn dữ liệu lớn, thời gian huấn luyện, tinh chỉnh mô hình kéo dài lâu hơn do tính phức tạp tăng lên khi các tham số dần lộ diện, và khuyết điểm lớn nhất cũng từ đây mà xuất hiện. Đó là “overfitting” – mô hình tìm được quá khớp với dữ liệu training khi quá nhiều tham số được đưa vào, dẫn đến đem lại kết quả thiếu chính xác nếu vận dụng vào thực tế.
Để hình dung lại rõ hơn các bạn cùng nhìn qua ví dụ sau, lấy bối cảnh chính chủ đề Survival analysis. Giả sử chúng ta xây dựng mô hình dự báo tỷ lệ rời dịch vụ của khách hàng hay còn gọi Churan rate, sẽ có 2 cách
Cách 1, nếu chúng ta biết những yếu tố nào sẽ tác động lên khả năng khách hàng rời bỏ công ty:
Parametric model:

Các tham số X chính là các yếu tố, các biến số tác động lên kết quả của biến mục tiêu Y mà ở đây là tỷ lệ khách hàng rời dịch vụ, và các hệ số β ở trước đóng vai trò định lượng những tác động ấy. Bên trên chính là phương trình tổng quát chung của các phương pháp phân tích hồi quy. Phương trình tham số tổng quát trên sẽ thay đổi dựa trên quy luật phân phối giả định từ tập dữ liệu.
Cách 2 nếu chúng ta chưa xác định được những yếu tố nào sẽ tác động lên khả năng khách hàng rời bỏ công ty, thay vì không thể dự báo dựa trên các yếu tố, chúng ta có thể sử dụng chính các function đã học và tiến hành ước lượng, rồi lấy kết quả đó đưa ra các phán đoán trong tương lai. Các chuyên gia gọi đây là ước lượng đường cong Survival hay Hazard.
Trở lại với Non-parametric model:

f(x) ở đây có thể là bất kỳ hàm nào, model nào được áp dụng để xác định giá trị của biến mục tiêu Y. Dữ liệu đưa vào phân tích sẽ định hình model phù hợp cần xây dựng và cho phép chúng ta tìm hiểu về đối tượng nghiên cứu, sử dụng đồ thị, biểu đồ trực quan.
Ở bài viết trước chúng ta đã tìm hiểu qua 2 function quan trọng của Survival analysis là Survival Function và Hazard Function:



và vì chúng ta chưa xác định được những yếu tố ảnh hưởng lên tỷ lệ rời dịch vụ của khách hàng, nên phải dựa vào Survival function để ước lượng thời gian khách hàng tiếp tục mua sản phẩm của công ty cho đến khi rời bỏ công ty.
Và may mắn các chuyên gia phân tích đã nghiên cứu và tìm được những phương pháp phi tham số hỗ trợ ước lượng tỷ lệ sống sót (sự kiện quan tâm không xảy ra) hay tỷ lệ rủi ro (sự kiện quan tâm sẽ xảy ra) trong Survival Analysis mà phổ biến nhất đó là Kaplan-Meier, Nelson-Aalen, Life table, và Log – rank.
Trong bài viết này chúng ta sẽ đi qua 3 phương pháp đầu tiên, còn Log – rank chúng tôi sẽ đề cập ở bài viết sau về Parametric methods, tuy Log – rank là phương pháp Non-parametric khá quan trọng nhưng do bài viết có giới hạn, và việc trình bày quá lý thuyết vào trong một bài viết cũng không hay nên mong các bạn thông cảm. Nếu tò mò về log-rank là gì và tại sao nó quan trọng các bạn có thể nghiên cứu trước, và hãy xem bài viết sắp tới của chúng tôi là công cụ hỗ trợ các bạn review lại kiến thức.
Các phương pháp phi tham số trong Survival analysis
Bên cạnh việc ước lượng Survival function và Hazard function, các phương pháp phi tham số đóng vai trò là công cụ mô tả dữ liệu, mô tả đối tượng nghiên cứu còn gọi Descriptive methods, khi các phương pháp này gắn liền với các biểu đồ, đồ thị trực quan, các bảng tóm tắt các thuộc tính đặc trưng của dữ liệu, của đối tượng, cũng như các số liệu thống kê. Ngoài ra chúng cho phép chúng ta xây dựng những giả thuyết, kết luận ban đầu và tiến hành kiểm định (ví dụ Log-rank dùng để so sánh sự khác biệt trong tỷ lệ sống sót giữa 2 nhóm)
Life table đơn giản
Như chúng ta đã biết trong thống kê khi tóm tắt dữ liệu đặc biệt là mẫu dữ liệu lớn khảo sát rất nhiều đối tượng, và đặc điểm của các đối tượng là khác nhau, do đó không thể sắp xếp một cách đơn giản như sắp xếp theo thứ tự từ A đến Z. Chúng ta phải tiến hành phân nhóm theo các tiêu chí định tính, định lượng để có một bảng tóm tắt tinh gọi, nhưng mô tả đầy đủ thông tin.
Trong Survival analysis cũng vậy, để ước lượng tỷ lệ sống sót, theo công thức đơn giản nhất là lấy số người còn sống chia cho tổng thể đang xét ở một khoảng thời gian cụ thể. Do đó chúng ta cần phân nhóm các khoảng thời để tìm hiểu ở mỗi khoảng thời gian đối tượng nào còn sống, đã chết, để tính toán tỷ lệ.
Và dĩ nhiện nếu dùng bảng dữ liệu thông thường trong đó liệt kê từng đối tượng, thời gian theo dõi và trạng thái của đối tượng thì khó có thể tính toán tỷ lệ. Vì vậy chúng ta cần sử dụng loại bảng mới, sử dụng đặc biệt cho Survival analysis đó là Life table.
Nói trịnh trọng như vậy, nhưng thực thất life table không quá phức tạp. Life table cũng hỗ trợ giải quyết vấn đề Censoring – dữ liệu thiếu thông tin, dữ liệu bị cắt xén do mất dấu theo dõi đối tượng nghiên cứu hay do thời gian nghiên cứu ngắn < thời gian sống sót tức kết thúc thời gian nghiên cứu mà sự kiện quan tâm (đối tượng đã chết) chưa xảy ra.
Trước khi đi vào ví dụ, chúng tôi làm rõ cách gọi tỷ lệ sống sót. “Sống sót” trong survival analysis không chỉ có mỗi ý nghĩa về khía cạnh sức khỏe, tính mạng, “sống sót” hay “chết”trong lĩnh vực khác có ý nghĩa khác. Như tập email gồm các email “sống”, “chết” tức các email còn sử dụng hay đã bị bỏ lâu. Trong dịch vụ, khách hàng “sống” còn có nghĩa là chưa rời dịch vụ và ngược lại với “chết”. Trong kỹ thuật, máy móc còn hoạt động nghĩa là “sống” và bị hỏng hóc, không thể hoạt động gọi là “chết”. Tuy nhiên một số trường hợp chúng ta không thể gọi là sống hoặc chết mà phải dùng “chưa xảy ra” và “đã xảy ra” ví dụ máy móc, thiết bị gặp lỗi, sản phẩm bị lỗi sau một khoảng thời gian.
Life table là một trong các phương pháp hữu hiệu tóm tắt thông tin về sự kiện quan tâm đã xảy ra đối với các đối tượng nghiên cứu như thế nào trong một khoảng thời gian theo dõi nhất định. Life table là phương pháp cổ điển nhất trong Survival analysis được ứng dụng chủ yếu trong lĩnh vực y tế xã hội như điều tra tỷ lệ tử vong dân số, vấn đề di dân, tỷ lệ thất nghiệp. Ở lĩnh vực khác như bảo hiểm, các công ty thường sử dụng Life table để ước tính tuổi thọ của khách hàng và điều chỉnh các quy định về phí bảo hiểm, tiền chi trả.
Để hiểu về phương pháp Life table chúng ta sử dụng ví dụ đơn giản trong lĩnh vực y tế
Ví dụ một bệnh viện theo dõi 20 bệnh nhân bị mắc bệnh ung thư trong thời hạn 3 năm, tức 36 tháng để nghiên cứu họ có thể sống được bao nhiêu tháng sau khi áp dụng phương pháp mổ loại bỏ khối u. Thời hạn theo dõi tối đa là 36 tháng, nếu bệnh nhân nào có thời hạn theo dõi < 36 tháng, hay lần cuối liên hệ là chưa tới 36 tháng (mất dấu, không có thông tin), hay sau 36 tháng vẫn cần theo dõi thêm (cần thêm thông tin) thì được coi là Censored.
Cách khác: chúng ta có thể chia 36 tháng thành các khoảng thời gian, và theo dõi trên từng giai đoạn, đối tượng nào có thời gian theo dõi nhỏ hơn/ hay lần cuối kiểm tra trạng thái nằm trong khoảng thời gian đang xét, có thể coi là Censored.
Lưu ý bạn nào không biết dữ liệu bị censored là gì có thể xem lại bài viết phần 1 để biết thêm.
Dưới đây là kết quả tổng hợp sau 3 năm, tức ở thời điểm cuối tháng thứ 36, cuối năm 3. Trong 20 người có 7 người tử vong, và chỉ có 2 người là được theo dõi đầy đủ và không tử vong còn lại 11 người là bị mất dấu. Như vậy có tất cả 13 Censored.

Trước tiên chúng ta sẽ chia 36 tháng thành J + 1 các khoảng thời gian bằng nhau, ký hiệu (tj – 1, tj) với j = 1, 2,…, J + 1. Để tính một khoảng thời gian bằng bao nhiêu đơn vị, lấy
bj~ = tj – tj – 1
Chúng ta sẽ có nj – 1 là số các đối tượng quan sát đưa vào theo dõi trong (tj – 1 , tj), dj là số lần sự kiện xảy ra trong khoảng thời gian j (tức số đối tượng đã trải qua sự kiện, mà ở ví dụ này là số bệnh nhân tử vong).
Trong trường hợp không có censored, không có đối tượng nào mất dấu, thì sự chênh lệch giữa nj – 1 tại tj – 1 và nj tại tj là do sự kiện đã xảy ra trong khoảng thời gian, như ví dụ trên chúng ta có bệnh nhân đã tử vong. Từ đó tỷ lệ giữa số đối tượng đã trải qua sự kiện/ số đối tượng được đưa vào nghiên cứu trong (tj – 1 , tj) chính là tỷ lệ rủi ro hay nguy cơ cần tìm.
Và trong trường hợp có censored, mẫu dữ liệu lúc này sẽ bị xáo trộn, chúng ta không thể lấy y nguyên số mẫu ở điểm bắt đầu khoảng thời gian để tính cho toàn bộ quá trình theo dõi do một số quan sát trong thực tế không được theo dõi nên không có thông tin.
Theo các chuyên gia, lúc này mẫu nên điều chỉnh theo công thức sau:

Với cj là số trường hợp bị Censored.
Đây là đặc điểm chính của life table mà được cho là hỗ trợ giải quyết vấn đề về Censoring. Life table tính toán số lần sống sót của các đối tượng bị censored hỗ trợ ước lượng tỷ lệ survival cho mẫu dữ liệu.
Tiếp tục, xác suất để sự kiện xảy ra, hay ở ví dụ này là xác suất tử vong. Xác suất này là xác suất có điều kiện do nó được tính dựa trên thông tin về số người sống sót qua từng khoảng thời gian.
Công thức như sau:

Như vậy xác suất sống sót hay tỷ lệ survival được tính bằng công thức:
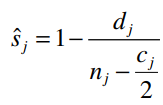
Survival function hay tỷ lệ survival tích lũy ở cuối giai đoạn (tj – 1 , tj) hay kết thúc một giai đoạn j nào đó được tính bằng công thức:
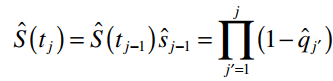
Ví dụ, tỷ lệ số bệnh nhân tham gia nghiên cứu sống sót ở thời điểm 0 (tức điểm bắt đầu quá trình theo dõi) là bằng 1. S0 = 1. Tiếp tục tỷ lệ số bệnh nhân sống sót qua gian đoạn 1 là S1 = P1*S0. Nghĩa là để sống sót qua giai đoạn 1, tức phải sống sót ở thời điểm 0. Tương tự S2 = P2*S1 = P2*P1*S0, tức để sống sót qua giai đoạn 2, thì phải sống sót qua thời điểm 0, và giai đoạn 1.
Đây là cách giải thích tại sao gọi xác suất tính được là xác suất có điều kiện và tích lũy.
Như vậy chúng ta đã tìm hiểu sơ về các công thức cơ bản của Life table đơn giản, cùng quay lại với ví dụ ban đầu, theo từng bước chúng tôi đề cập ở trên chúng ta có kết quả sau:

Trước tiên chúng ta tóm tắt số người sống sót, số tử vong, và trường hợp bị censored. Trong 6 tháng đầu, có 2 người tử vong (ID3/ 5 và ID10/ 6) và 0 có censored, tiếp tục từ tháng thứ 7 đến hết tháng 13 có 2 người tử vong (ID6/ 9 và ID14/ 12) và có 2 censored (ID7/ 13 và ID8/ 11). Các bạn làm tương tự.

Áp dụng theo các công thức đã giới thiệu các bạn sẽ có kết quả như trên, lưu ý xác suất sống sót tích lũy ví dụ S(7-13) = 0.9*0.88 = 0.79.
Như vậy xác suất sống sót sau 3 năm của một bệnh nhân ung thư áp dụng phẫu thuật là 42%
Ngoài các công thức đơn giản trên để tính phương sai hay độ lệch chuẩn (căn bậc 2 của phương sai) chúng ta cũng có các công thức sau. Ở các phần mềm phân tích, thống kê hiện nay như SPSS đều tính sẵn.
Phương sai của qj
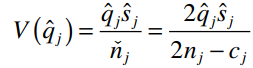
Phương sai của St
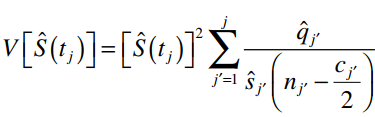
Tiếp theo, life table không chỉ được dùng để tính toán mỗi tỷ lệ sống sót, mà nó còn áp dụng để tính tỷ lệ rủi ro. Lưu ý tỷ lệ rủi ro ở đây, tính trên đơn vị thời gian, nó không phải là xác suất, không thể lấy 1 – sj, khi sj lại tính theo khoảng.
Và theo bài viết trước, vì tỷ lệ rủi ro theo công thức Hazard function tính trên khoảng thời gian theo dõi đối tượng bị giới hạn dần về 0, tức tính trên đơn vị thời gian (unit) như ngày, tháng,… chứ không tính theo khoảng. Do đó thay vì tìm tỷ lệ tử vong trên khoảng (tj – 1 , tj), chúng ta tìm thời điểm là điểm chính giữa tmj hay còn gọi Mid-point
Công thức tính tỷ lệ Hazard tại tmj
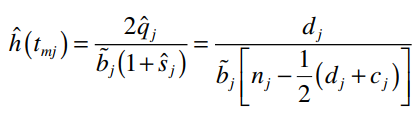
Với:
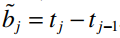
Phương sai của tỷ lệ Hazard tại tmj
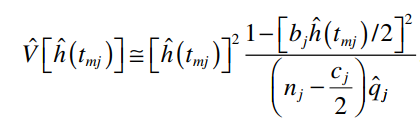
Chúng ta đã làm quen với ví dụ trong lĩnh vực y tế, giờ chúng ta sẽ sang một ví dụ trong lĩnh vực kinh tế. Đây là ví dụ điển hình nói về vấn đề churn, khách hàng rời dịch vụ trong ngành viễn thông và được IBM sử dụng để giới thiệu về Survival analysis trong phần mềm SPSS Statistics và SPSS modeler.
Dữ liệu gồm 1000 đối tượng quan sát, là các khách hàng sử dụng dịch vụ viễn thông của một công ty, gồm 43 biến hay thuộc tính mô tả đặc điểm, cung cấp thông tin về từng khách hàng.
Ở ví dụ này chúng ta quan tâm 3 biến quan trọng là Tenure (số tháng khách hàng sử dụng dịch vụ của công ty) với giá trị tính theo số tháng, Customer Category (loại khách hàng) dựa trên loại dịch vụ sử dụng với 1: “Basic service” 2: “E- Service”, 3: “Plus service”, và 4: “Total service”, và biến Churn với 1: khách hàng đã rời dịch vụ (không còn đăng ký sử dụng) và 0: khách hàng chưa rời dịch vụ. Dưới đây là mẫu dữ liệu ví dụ:
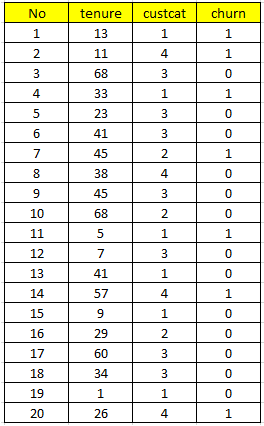
Sử dụng các phần mềm phân tích như SPSS, chúng ta không cần xác định Censored, SPSS sẽ thực hiện việc này chỉ cần các bạn xác định các khoảng thời gian (tj – 1 ; tj) sẽ được chia thế nào, và chỉ định biến thời gian theo dõi các đối tượng, ở đây là Tenure. Nếu đối tượng có thời gian theo dõi hay nói cách khác thời gian sử dụng dịch vụ được ghi nhận nằm trong khoảng thời gian (tj – 1 ; tj) thì có thể coi là Censored vì khả năng một là họ còn sử dụng dịch vụ mà công ty không theo dõi thêm hoặc hai là đã bị mất dấu.
Ví nhìn ở mẫu dữ liệu trên, từ (0; 12) từ thời điểm bắt đầu theo dõi cho đến tháng thứ 12, có 5 khách hàng có thời gian sử dụng dịch vụ trong khoảng này (No: 2, 11, 12, 15, 19) và chỉ có khách hàng No: 2, 11 là đã rời dịch vụ, còn lại là khách hàng No: 12, 15, 19 có thời hạn sử dụng dịch vụ lần lượt là 7, 9 và 1 tháng thì khả năng họ vẫn còn sử dụng hoặc công ty đã bỏ theo dõi.
Chúng ta sử dụng biến Customer category làm biến yếu tố để so sánh tỷ lệ sống sót tại các nhóm khách hàng khác nhau là như thế nào. Thời gian chia thành các khoảng với độ dài bj = 3 tháng
Kết quả phân tích Life table từ SPSS
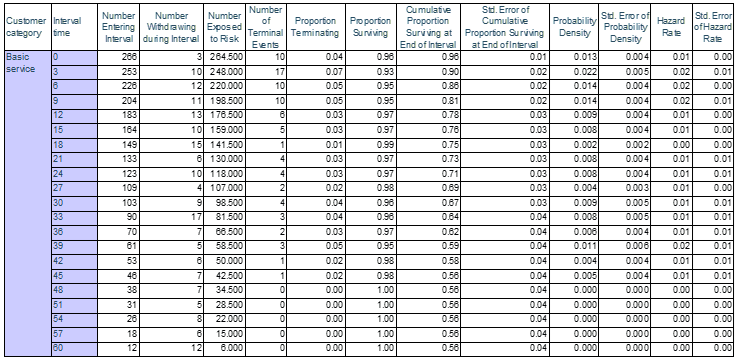
Bên trên là kết quả mẫu của nhóm Basic Service, Interval time là khoảng thời gian (tj – 1 ; tj), bằng 0 tức tj-1 = 0 và tj = 3, tức là từ (0; 3). Number entering interval chính là nj, Number withdrawing during interval chính là censored cj, Number exposed to risk là mẫu đã được hiệu chỉnh nj^, Number of Terminal events là số khách hàng đã churn tức rời dịch vụ, Proportion Terminating là qj, Proportion Surviving là sj, Cumulative Proportion Surviving là Sj cột kế bên Std error là độ lệch chuẩn Sj (căn 2 của phương sai theo công thức V[Sj] ở trên), Probability Density là xác suất khách hàng rời dịch trong suốt khoảng thời gian (tính từ hàm mật độ xác suất tại điểm chính giữa tmj của (tj – 1 ; tj) và cột kế bên là độ lệch chuẩn. Công thức như sau:
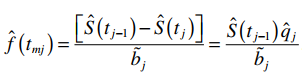
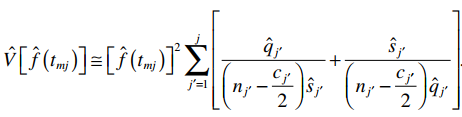
Hazard rate và độ lệch chuẩn của nó công thức chúng tôi cũng đã đề cập trên. Các bạn thử tính nhé.
Như vậy chúng ta có bảng life table, ngoài ra để mô tả trực quan khi dữ liệu quá lớn, dựa vào các phần mềm chúng ta có thể vẽ được đồ thị mô tả đường cong sống sót.
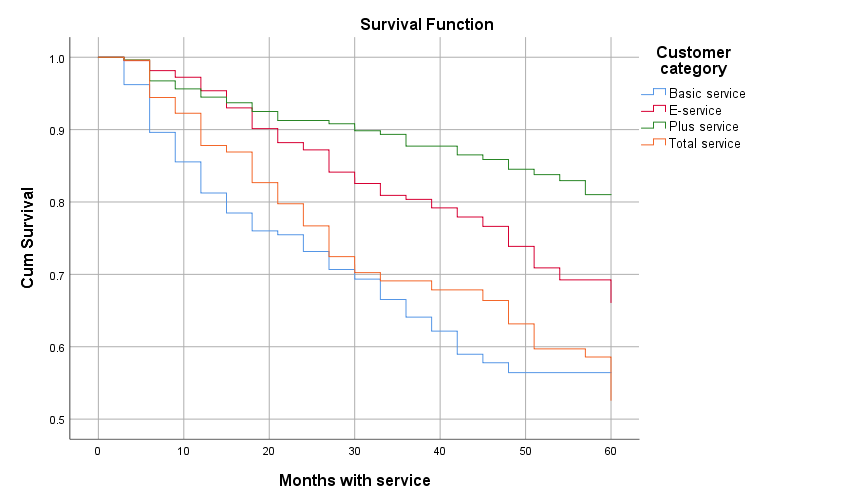
Trục hoành là thời gian, trục tung là xác suất. Tại các điểm gãy là xác suất sống sót tích lũy tại thời điểm bắt đầu và xác suất này sẽ tồn tại đến thời điểm kết thúc giai đoạn, mô tả tỷ lệ survival trong 1 khoảng thời gian. Vì thế đồ thị nhìn giống bậc thang hơn là đường cong. Như theo bảng kết quả, tỷ lệ khách hàng không rời dịch vụ trong 3 tháng đầu, xét cho phân khúc Basic Service là 0.96 (0; 3), 6 tháng đầu là 0.9 (3; 6), 9 tháng đầu là 0.95 (6; 9).
Nhìn qua đồ thị chúng ta thấy tỷ lệ khách hàng rời dịch vụ ở Basic Service và Total Service là khá cao, khi đường cong survival giảm mạnh và nhanh khi thời gian sử dụng tăng. Plus Service là có tỷ lệ churn thấp nhất khi đường cong survival giảm với tốc độ chậm, với mức độ rất nhỏ. Từ kết quả trên, các chuyên gia kinh doanh trong công ty sẽ phải xem xét nguyên nhân tại sao như vậy và giải pháp để giữ chân 2 nhóm khách hàng có tỷ lệ churn cao. Thông qua ví dụ này có lẽ các bạn đã hiểu hơn ứng dụng của Survival analysis và tầm quan trọng của việc mô tả tỷ lệ churn.
Kaplan – Meier và Nelson – Aalen
Tiếp tục với phương pháp tiếp theo Kaplan – Meier, được đặt tên theo các chuyên gia phân tích đã nghĩ ra phương pháp này năm 1958. Nếu các bạn đã hiểu về Life table thì sẽ nhanh chóng nắm bắt được phương pháp này.
Một trong các vấn đề khi sử dụng phương pháp Life table đó là khi chúng ta tinh chỉnh các khoảng thời gian hay nói cách khác thay đổi cách chia thời gian để theo dõi thì tỷ lệ sống sót. Đặc biệt khi mẫu dữ liệu nhỏ, nó sẽ tác động lên kết quả tính được.
Kaplan – Meier (KM) khắc phục khuyết điểm trên của Life table khi nó ước tính lại tỷ lệ sống sót mỗi lần xảy ra sự kiện, và nó không bắt buộc chia các khoảng thời gian thành các giai đoạn bằng nhau. Để hiểu hơn chúng ta cùng đi qua ví dụ sau:
Giả sử chúng ta có 10 bệnh nhân mắc ung thư và thời điểm tử vong (khoảng thời gian từ lúc theo dõi cho đến khi tử vong) kể từ lúc theo dõi được ghi nhận lần lượt như sau: 6, 10, 12, 16, 20, 25, 28, 30, 32, 36. Thời gian theo dõi tối đa là 3 năm, tính theo tháng.
Trường hợp này chưa nói đến Censoring, các bạn có thể thấy cách tính khá đơn giản dễ hiểu, nó giống Life table nhưng không tính trên khoảng thời gian. Tại mỗi thời điểm có người tử vong, chúng ta sẽ lại tính tỷ lệ sống sót tích lũy.
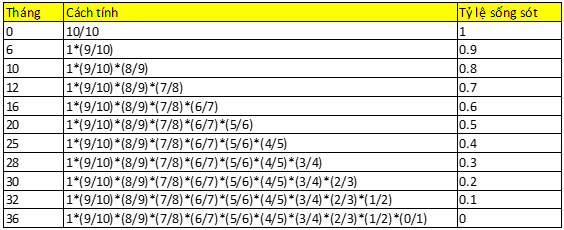
Chúng ta đến với trường hợp có censoring. Giả sử thêm vào 2 bệnh nhân lần lược được theo dõi đến tháng thứ 18 và 23, rồi mất dấu.

Tại thời điểm tháng 18, 1 bệnh nhân bị mất dấu, ký hiệu + nghĩa là censored, ở thời điểm này, chúng ta đã mất 4 bệnh nhân lần lược ở tháng thứ 6, 10, 12, 16, vậy còn 8 bệnh nhân, tuy nhiên tại tháng 18, lại mất dấu 1 bệnh nhân, nên còn 7 bệnh nhân, mặc dù vậy tại tháng thứ 18 này chúng ta không mất bệnh nhân nào nữa nên tỷ lệ sống sót sẽ là 7/7, tương tự như ở tháng thứ 23. Dễ hiểu phải không nào?
Công thức xác suất sống sót tích lũy của phương pháp KM như sau:
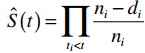
Các bạn có thể thấy cách tính và không thức gần giống với life table chỉ khác ở chỗ KM tính tỷ lệ sống sót vào thời điểm xảy ra sự kiện và sự kiện đó có thể là bệnh nhân tử vong, khách hàng rời dịch vụ và cả Censoring.
KM dùng xác suất tích lũy vì nó giả định nếu một bệnh nhân sống sót vào tháng thứ 32, ví dụ như vậy, thì họ sẽ phải sống sót từ tháng 0 đến tháng 32.
Bên cạnh tìm tỷ lệ sống sót tích lũy sử dụng KM, chúng ta cũng có thể tìm được tỷ lệ rủi ro tích lũy theo công thức ước lượng Nelson – Aalen cũng được đặt tên bởi chính 2 chuyên gia tìm ra nó Nelson (1972), Aalen (1978)
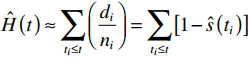
Hoặc chúng ta sử dụng công thức đã nhắc đến phần 2 bài viết trước.
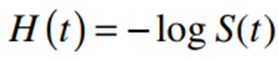
Kết quả của 2 công thức sẽ xấp xỉ nhau:
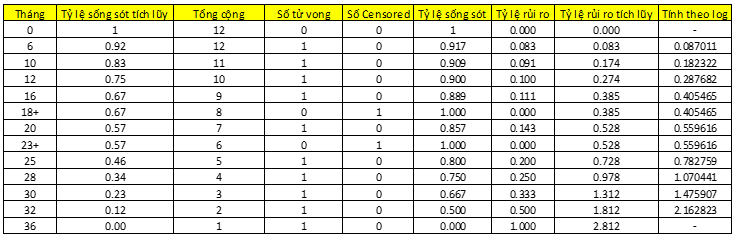
Tỷ lệ rủi ro cho từng thời điểm chúng ta lấy số bệnh nhân tử vong chia cho tổng cộng số quan sát còn lại sau khi đã loại bỏ các bệnh nhân tử vong trước đó cũng như censoring. Sau đó tính tổng hay cộng dồn với các mốc trước để tìm. Tuy nhiên cách nhanh nhất vẫn là lấy – log của tỷ lệ sống sót tích lũy. Các phần mềm phân tích như SPSS thường sử dụng công thức log để tính nên chúng ta cứ sử dụng.
Ngoài ra lý do sử dụng log là để các bạn tránh nhầm lẫn Hazard rate không phải là xác suất ở một số trường hợp nếu chúng ta tập trung tính theo đơn vị thời gian và khi đơn vị thời gian thay đổi tỷ lệ hazard > 1. Chi tiết các bạn xem lại bài viết phần 2. Còn ở bảng kết quả trên, tỷ lệ rủi ro chúng ta tính cố định theo tháng, và sử dụng công thức (dj/ nj) nên có thể coi là xác suất.
Chúng ta quay trở lại với ví dụ của công ty viễn thông ở trên:
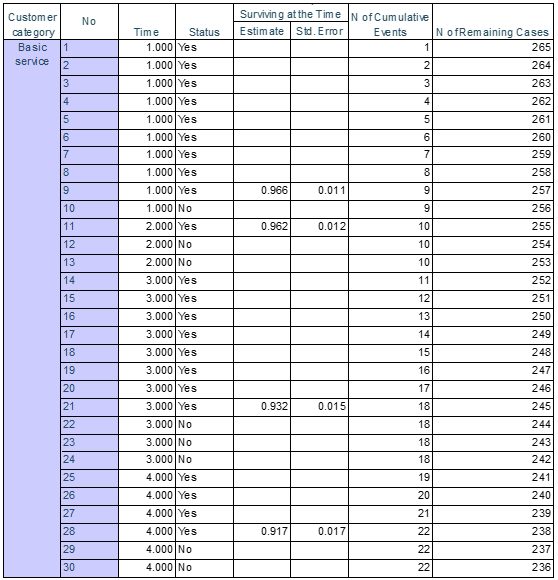
Với nhóm khách hàng Basic service chúng ta có 266 khách hàng, trong bảng trên chúng tôi lấy ví dụ kết quả cắt ra cho của 30 khách hàng. Cột No là số thứ tự khách hàng, time là thời điểm xét đến, đơn vị là tháng, Status là trạng thái, Yes: rời dịch vụ, No: chưa rời dịch vụ (có thể khách hàng còn sử dụng dịch vụ, hoặc đã mất dấu, có thể là censored), Surviving at time là xác suất sống sót tích lũy được ước lượng, còn Standard error là độ lệch chuẩn theo công thức sau:
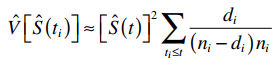
Đối với độ lệch chuẩn của Hazard rate theo phương pháp Nelson – Aalen cung cấp thêm cho các bạn
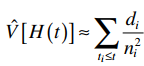
Quay trở lại với bảng kết quả, Number of Cumulative events là số khách hàng đã rời dịch vụ tích lũy đến thời điểm đang xét, Number of remaining cases tức là số khách hàng còn lại cần xét đã loại bỏ trường hợp Censored, tức khách hàng có status: No
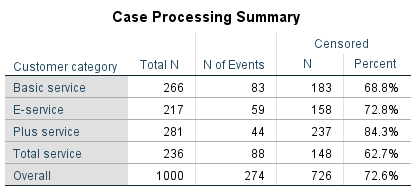
Bên trên là bảng tóm tắt thông tin từng nhóm dịch vụ có bao nhiêu khách hàng, số khách hàng đã rời dịch vụ và số khách hàng bị mất dấu Censored.
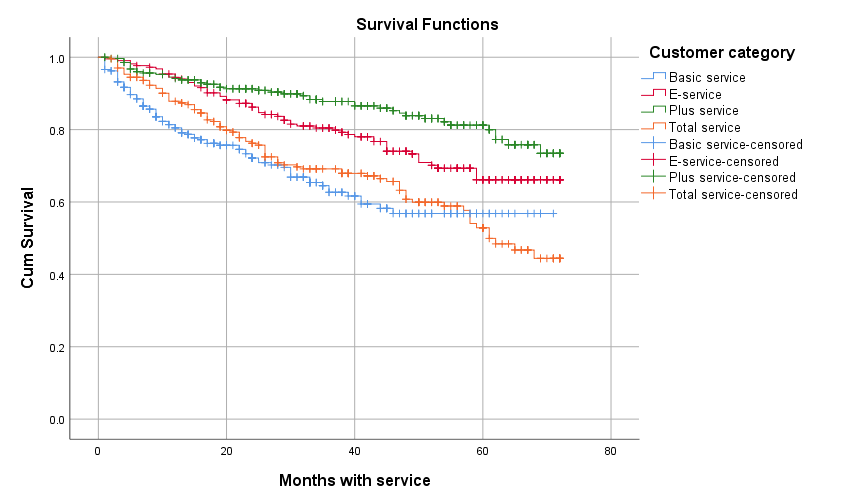
Do KM tính tỷ lệ sống sót cho cả sự kiện censoring, nên các bạn có thấy trên đồ thị nó thể hiện luôn đường cong sống sót cho trường hợp censoring.
Trong 2 ví dụ chúng tôi đề cập phần đầu phương pháp KM, khi chúng ta có censoring ở các thời điểm t, mà không có bệnh nhân nào khác tử vong thì tỷ lệ sống sót được giữ nguyên, căn cứ theo mốc thời gian trước đó. Nó chỉ thay đổi khi ngoài censoring có thêm sự kiện được quan tâm xảy ra hoặc không có censoring chỉ sự kiện được quan tâm xảy ra.
Thông qua cách giải thích của chúng tôi, các bạn đã hiểu tại sao kết quả ở trên, chỗ surviving at time có nhiều dòng không có giá trị?
Khách hàng nào đóng vai là người cuối cùng rời dịch vụ ở thời điểm t hay trong khoảng thời gian t tháng, thì tại khách hàng này chúng ta chỉ cần tính xác suất sống sót tích lũy. Và xác suất này sẽ giữ nguyên khi gặp trường hợp khách hàng censored, và được tính lại khi bắt đầu có khách hàng rời dịch vụ.
Mặc dù đồ thị KM cung cấp khác với Life table, nhưng nó vẫn đưa ra các kết luận giống nhau. Plus service vẫn là nhóm khách hàng có tỷ lệ rời dịch vụ thấp nhất, cao nhất vẫn là Basic service, tiếp đến là Total service.
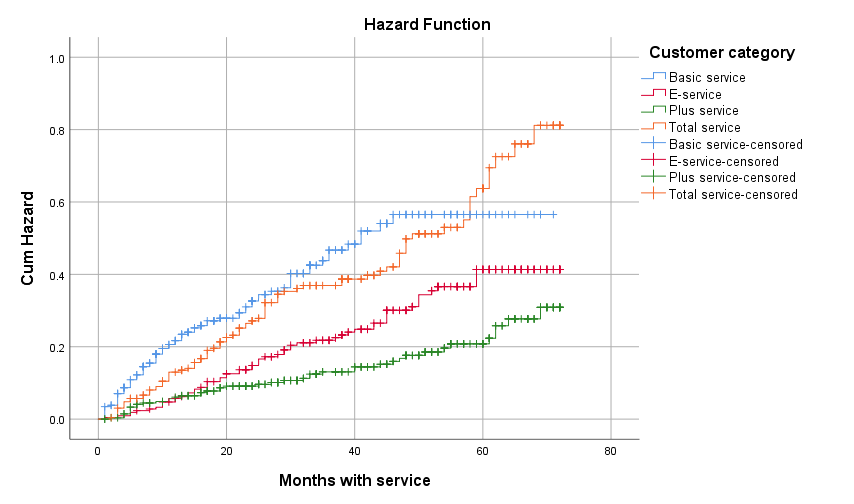
Ngoài đồ thị cho Survival function, các bạn có thể sử dụng thêm đồ thị cho Hazard Fucntion để phân tích nhóm khách hàng nào có rủi ro rời dịch vụ cao nhất
Bên cạnh các công thức xác định độ lệch chuẩn cho tỷ lệ sống sót tích lũy hay rủi ro tích lũy, chúng ta cũng cần quan tâm đến các tham số như Mean, Median, khoảng tin cậy (Confidence Interval) để mô tả chi tiết và chính xác hơn về các đối tượng nghiên cứu trong Survival analysis. Do bài viết có hạn nên chúng tôi không thể trình bày tại đây, các bạn nên tham khảo thêm ở các tài liệu khác.
Như vậy đến đây là kết thúc bài viết phần 3. Hẹn gặp cái bạn ở bài viết sắp tới, về Log rank và Cox PH Regression (Phần 1)
Tài liệu tham khảo:
“Survival Analysis” – Lisa Sullivan
“An Introduction to Survival Analysis” – Mario Cleves và cộng sự
“Survival Analysis A Practical Approach” – David Machin và cộng sự
“Survival Analysis – Models and Applications” – Xian Liu và cộng sự
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English