Ở 2 bài viết trước BigDataUni đã giới thiệu đến các bạn thuật toán Classification đầu tiên là KNN (K – nearest neighbor) và một số phương pháp đánh giá mô hình phân loại như Hold out, Cross validation, hay Confusion matrix, Lift, Gain chart, ROC/ AUC. Trở lại với chủ đề về những thuật toán phân loại trong Data mining, lần này chúng tôi và các bạn sẽ tìm hiểu về Decision Tree, thuật toán có thể nói là “nổi tiếng”, “phổ biến” mà bất kỳ ai hoạt động và làm việc trong lĩnh vực khoa học dữ liệu, hoặc phân tích dữ liệu đều phải biết đến. Nguyên nhân là vì Decision Tree thể hiện tính đơn giản, trực quan, và có nhiều ứng dụng cụ thể trong thực tế. Bài viết hôm nay, chúng tôi sẽ trình bày khái quát về thuật toán “cây quyết định” với dạng đầu tiên là CART (Classification & Regression Tree) bao gồm bản chất, công thức hay cách triển khai thuật toán trên ví dụ cụ thể.
Lưu ý bài viết nghiêng nhiều về lý thuyết nhiều hơn thực hành vì mục đích chia sẻ kiến thức nền tảng của Data mining cụ thể là các thuật toán phân loại đến những bạn đang tiếp cận, theo học lĩnh vực này, biết về Decision Tree (CART) nhưng chưa nắm kiến thức cơ bản. Tuy nhiên, trong quá trình diễn giải về thuật toán, chúng tôi vẫn sẽ cung cấp ví dụ để thông qua đó các bạn sẽ dễ hiểu hơn, có cái nhìn tổng quan hơn về phương pháp tiếp cận của các mô hình Classification trong khai phá dữ liệu. Đầu tiên trước khi đi vào nói về CART, chúng ta sẽ cùng tìm hiểu về sơ qua về thuật toán Cây quyết định.
Decision Tree là một thuật toán thuộc loại Supervised Learning, phương pháp học có giám sát, kết quả hay biến mục tiêu của Decision Tree chủ yếu là biến phân loại. Các thuật toán được xây dựng giống hình dạng một các cây có ngọn cây, thân cây, lá cây kết nối bằng các cành cây, và mỗi thành phần đều có ý nghĩa riêng của nó, như các yếu tố tác động lên quyết định sau cùng.
Xét về khía cạnh trong lĩnh vực dữ liệu, hồi quy (regression) và phân loại (classification) là hai phương pháp Data mining có thể được thực hiện thông qua Decision tree hay nói cách khác Decision tree có thể được áp dụng cho cả 2 dạng phân tích trong các dự án nghiên cứu khác nhau. Vì tính chất này mà khi nhắc đến Decision tree, cây quyết định, thông thường thì người ta thường gọi Classification & Regression Tree viết tắt là CART. Trong bài viết lần này chúng tôi chỉ đề cập đến CART phục vụ cho phân loại dữ liệu với biến định tính, còn Regression chúng tôi sẽ gửi đến các bạn trong các bài viết sắp tới.
Decision Tree là thuật toán được xây dựng trên mô hình một các cây mục đích để thể hiện kết cấu, sự cấu trúc của một hệ thống ra quyết định, hay nói cách khác cách con người tư duy, logic ra sao để đi đến quyết định cuối cùng. Còn trong lĩnh vực dữ liệu, Decision Tree thể hiện mối quan hệ giữa các yếu tố (các biến độc lập), và sự tác động của chúng như thế nào đến biến mục tiêu. Các bạn cùng nhìn qua 2 hình ví dụ dưới đây
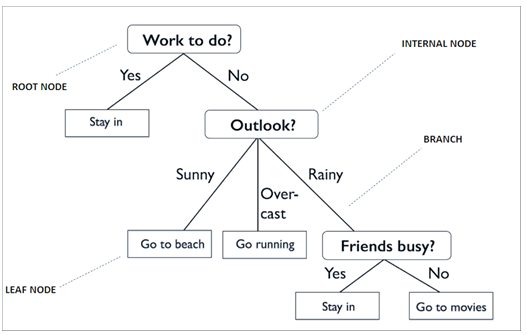
(Nguồn hình Towardsdatascience)
Decision tree đơn giản trong việc ra quyết định chọn lựa giữa đi chơi và ở nhà trên cơ sở xem xét các tình huống có thể xảy ra của thời tiết hay các vấn đề khác. Nếu giải thích ở khía cạnh dữ liệu, thì “Work to do?”, “Outlook”, “Friends busy?” chính là các biến độc lập có thể tác động đến biến mục tiêu ví dụ đặt tên là “Decision” chứa các giá trị Stay in, Go to beach, Go running, Go to movies. “Work to do?” có 2 giá trị là Yes và No, nếu Yes thì người này chắc chắn ở nhà và không còn quyết định nào khác trừ ở nhà và làm việc nên chỉ có 1 nhánh. Còn nếu No thì có thể người này ra ngoài chơi, tuy nhiên còn phải xét đến thời tiết. Tương tự như thế mà cái cây được hình thành cho đến khi không còn trường hợp để xét và quyết định khác cần đưa ra. Các bạn nhìn kỹ sẽ thấy, mỗi giá trị trong một biến độc lập đều có thể tác động lên quyết định sau cùng tạo nên sự liên kết, hay mối liên hệ với biến mục tiêu. Nhìn trên hình chúng ta có thể thấy một cây quyết định bao gồm:
- “Root node”: điểm ngọn chứa giá trị của biến đầu tiên được dùng để phân nhánh.
- “Internal node”: các điểm bên trong thân cây là các biến chứa các thuộc tính, giá trị dữ liệu được dùng để xét cho các phân nhánh tiếp theo
- “Leaf node”: là các lá cây chứa giá trị của biến phân loại sau cùng.
- “Branch” là quy luật phân nhánh, nói đơn giản là mối quan hệ giữa giá trị của biến độc lập (Internal node) và giá trị của biến mục tiêu (Leaf node).
Bên trên là trường hợp ứng dụng Decision Tree trong cuộc sống hàng ngày, vậy còn trong Data mining, hay Machine learning thì sao?
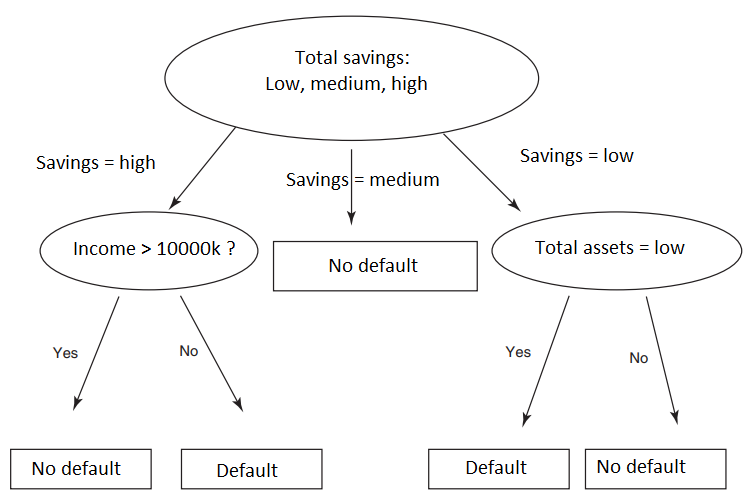
Ví dụ bên trên minh họa cho ứng dụng của Decision tree trong lĩnh vực ngân hàng dự báo khả năng khách hàng có thể không trả được nợ “Default”, hoặc thanh toán được “nợ” “No default” dựa trên các thông tin về khoản tiết kiệm “Savings”, thu nhập “Income”, và tài sản “Assets”. Nếu savings = medium, tức khách hàng có khoản tiết kiệm trung bình thì chắc chắn sẽ không có nợ xấu, nếu khách hàng có khoản tiết kiệm ít chúng ta phải xét thêm liệu tài sản của khách hàng có nhiều hay không trường hợp do khách hàng sử dụng tiền tiết kiệm để mua sắm nên vẫn có tài sản thế chấp, ngược lại nếu giá trị tài sản thấp, khả năng cao khách hàng khó trả được nợ. Tương tự vậy chúng ta xét tiếp cho thu nhập.
Đừng lầm tưởng rằng chỉ cần nhìn lên sơ đồ trên mà các bạn có để dự báo, phân loại chính xác khả năng khách hàng nợ xấu ví dụ nhiều bạn sẽ chủ quan cho rằng tiết kiệm nhiều cùng với thu nhập cao chắc chắn sẽ có khả năng trả nợ. Các bạn khác sẽ thắc mắc tại sao từ khoản tiết kiệm trung bình mà cây quyết định có thể khẳng định khách hàng sẽ trả được nợ tức “No default” và không xét tiếp yếu tố khác. Hoặc tại sao cây quyết định lại không đề cập đến các biến độc lập khác? Đầu tiên thuật toán Decision tree là thuật toán phân loại, Classification, nhớ lại các bài viết trước chúng tôi đã đề cập thì khi thực hiện phân tích phân loại trong Data mining, chúng ta phải có trước một tập dữ liệu đầy đủ, trong đó có biến mục tiêu và các giá trị, thuộc tính của nó. Ví dụ ở đây, chúng ta phải có trước tập dữ liệu khách hàng trước đây mà ngân hàng từng giao dịch, và có kết quả phân loại những khách hàng nào không trả được nợ, hay thanh toán hết nợ. Dựa vào đó để xem xét các đặc điểm, yếu tố, nguyên nhân nào dẫn đến kết quả phân loại ấy, trình tự ra sao, và tiến hành thực hiện thuật toán Decision Tree. Sau đó khi có khách hàng mới với dữ liệu cá nhân thu thập sẵn, với Decision tree, ngân hàng có thể đưa ra dự báo rủi ro tín dụng từ nhóm khách hàng mới này thông qua việc phân loại khách hàng vào các nhóm có rủi ro hoặc không có rủi ro.
Quá trình phân chia nhánh cây trong mô hình cây quyết định đều dựa trên các công thức tính toán, định lượng rõ ràng, sao cho quá trình này sẽ đem lại kết quả tối ưu nhất. Chúng tôi sẽ trình bày cụ thể ngay sau phần này.
Nhiệm vụ sau cùng của Decision tree hay bất kỳ thuật toán Classification nào khác chính là phân loại đối tượng dữ liệu chưa được phân loại trước đó vào các nhóm, các lớp phù hợp. Xét về số nhánh thì có 2 dạng cây quyết định bao gồm cây chỉ phân được 2 nhánh và cây phân được nhiều nhánh khác nhau. Các ví dụ ở trên là dạng cây phân được nhiều nhánh, thì phổ biến hiện nay có CHAID, và C4.5, C5.0 là các thuật toán xây dựng Decision tree nhiều nhánh.
Ở phần 1 bài viết lần này chúng tôi sẽ đề cập ban đầu đến thuật toán CART dùng cho Classification, cây quyết định chỉ phân được 2 nhánh mỗi lần. Tương tự như CART, chúng ta còn có QUEST nhưng khác biệt ở biến mục tiêu, giá trị ở của phân nhánh cuối cùng của QUEST chỉ có thể là biến định tính: Categorical, và biến thay phiên: Nominal hoặc Flag như “Có” hoặc “Không”, “No Default” hoặc “Default”, còn CART, biến mục tiêu có thể là bất kỳ biến từ định lượng, đến định tính, hay thay phiên.
Tóm lại, Decision tree là một trong những phương pháp Data mining, cụ thể Classification được sử dụng nhiều nhất trong các dự án nghiên cứu dữ liệu, là phương pháp Supervised learning – học có giám sát hiệu quả nhất vì nó mang lại kết quả dự báo, phân loại chính xác, ổn định, dễ diễn giải. Khác với các phương pháp hồi quy thông thường, Decision tree còn có khả năng thể hiện cả mối liên hệ phi tuyến giữa các biến dữ liệu một cách hiệu quả do đó được ứng dụng trong mọi khía của lĩnh vực khoa học dữ liệu, và là mảng kiến thức quan trọng mà bất kỳ chuyên gia phân tích nào phải có.
Trước khi triển khai thuật toán Decision trees, thì quy trình phân tích hay mô hình dữ liệu phải thỏa mãn các yêu cầu sau:
- Tập dữ liệu phải đạt đủ chất lượng trước khi đưa vào phân tích, được chia thành các tập training và test sao cho phù hợp, với tập training thì phải có đầy đủ biến phân loại, biến mục tiêu (target variable), còn test data thì không có.
- Tập dữ liệu training phải dồi dào, đa dạng về các biến, thuộc tính dữ liệu để quá trình huấn luyện cho mô hình diễn ra tối ưu và kết quả phân loại chính xác.
- Các lớp, các nhóm hay giá trị của biến mục tiêu phải rời rạc, rõ ràng. Thông thường không thể áp dụng phân tích cây quyết định cho một biến mục tiêu liên tục (continuous variable). Thay vào đó, biến mục tiêu phải nhận các giá trị được phân định rõ ràng là thuộc về một lớp, nhóm cụ thể nào đó hoặc không thuộc về một lớp, nhóm cụ thể nào đó. Ví dụ phân loại khách hàng theo thu nhập, giả sử phạm vi giá trị của biến mục tiêu tức thu nhập của khách hàng từ 3 triệu đến hơn 100 triệu thì chúng ta nên phân thành các nhóm thu nhập như thế nào?
Bây giờ chúng ta sẽ đi vô chi tiết thuật toán CART, dựa trên ví dụ đơn giản ứng dụng trong việc phân loại khách hàng có rủi ro tín dụng (không có khả năng thanh toán nợ) hay không có rủi ro tín dụng (có khả năng thanh toán nợ), giống như ví dụ trong bài viết về thuật toán KNN (K nearest neighbor).
Các bạn có thể tham khảo lại bài viết theo link dưới đây:
Thuật toán KNN và ví dụ đơn giản trong ngành ngân hàng
Quay trở lại với mô hình cây quyết định về phân loại khách hàng theo “No Default” hay “Default”, tại sao lại chọn Total savings là điểm bắt đầu phân nhánh mà không chọn Assets hay Income? Tại sao nhánh bên trái lại là Income > 10000k mà không phải <10000k tương tự như Assets phía bên phải, tại sao chúng ta không xét Assets = high?
Thuật toán cây quyết định được xây dựng để cố gắng tìm ra một tập hợp các “nhánh lá” tối ưu nhất, nghĩa là nếu các đối tượng trong tập dữ liệu có cùng 100% một thuộc tính A của một biến nào đó mà đều được phân loại theo một thuộc tính B bất kỳ của biến mục tiêu, thì gọi là “nhánh lá” thuần khiết, trong Data mining có thuật ngữ là “pure leaf node”.
Ví dụ nếu trong tập training mẫu có 20 khách hàng có thu nhập trên 20 triệu, và đều được phân loại là không có rủi ro tính dụng, thì trên cây quyết định, node “thu nhập” khi phân nhánh đầu tiên “thu nhập trên 20 triệu” sẽ tiếp tục phân nhánh tiếp đến “không có rủi ro tín dụng” và dừng ngay tại đây. Node “không có rủi ro tín dụng” này sẽ là “pure leaf node”. Cũng giống như ở mô hình cây quyết định thứ 2 trong bài viết, “savings = medium” => “No Defualt” – là “pure leaf node”, do đó khi Total savings có “pure leaf node” sẽ được đưa lên thành “Root node”.
Vậy bằng cách nào mà thuật toán có thể xác định được tính đồng nhất, hoặc ngược loại không đồng nhất của các dữ liệu trong node? Và làm cách nào để phân chia các nhánh tiếp theo nếu không có “pure leaf node”?
Phương pháp CART được giới thiệu lần đầu tiên vào năm 1985 bởi nhà thống kê Leo Breiman và các cộng sự của ông. CART chủ yếu được dùng để xây dựng Decision tree chỉ phân theo hai nhánh mỗi một lần. CART chia bộ dữ liệu training thành những tập con, bên trong có các đối tượng dữ liệu có cùng thuộc tính làm cơ sở cho việc phân loại.
CART, hay các thuật toán cây quyết định khác hoạt động dựa trên nguyên lý là làm sao để chọn ra các node chứa các đối tượng dữ liệu có khả năng tương đồng với nhau để xác định các nhóm, các lớp phù hợp cho các đối tượng này. Do đó, khi xây dựng một thuật toán cây quyết định bất kỳ, các chuyên gia phải sử dụng một trong các công thức dưới đây để tính toán tính đồng nhất của mỗi node và dùng kết quả có được để tìm ra cách phân nhánh “split” tối ưu nhất Công thức xác định “goodness” của mỗi cách phân nhánh:

Công thức hệ số GINI:
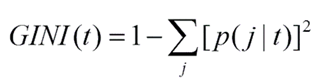
Công thức Entropy:
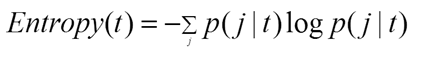
Công thức dựa trên xác định tỷ lệ sai sót trong phân loại:
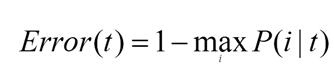
Trong bài viết lần này, chúng tôi sẽ trình bày thuật toán CART theo công thức đầu tiên, còn các công thức còn lại chúng tôi sẽ trình bày ở bài viết tiếp theo ví dụ như trong bài viết về thuật toán C4.5 chúng tôi sẽ nói về công thức Entropy. Quay trở lại với công thức đầu tiên, “Goodness of best split”

- tL là node bên trái của phân nhánh đầu tiên của root node trong cây quyết định
- tR là node bên phải của phân nhánh đầu tiên của root node trong cây quyết định
- PL là tỷ lệ của số quan sát của node bên trái tL trên tổng số quan sát của tập dữ liệu tranining
- PR là tỷ lệ của số quan sát của node bên phải tR trên tổng số quan sát của tập dữ liệu tranining
- P(j/tL) là tỷ lệ của số quan sát có thuộc tính j (của biến mục tiêu) trên tổng số quan sát trong node bên trái.
- P(j/tR) là tỷ lệ của số quan sát có thuộc tính j (của biến mục tiêu) trên tổng số quan sát trong node bên phải.
- Cách phân nhánh nào có giá trị cao nhất được tính từ công thức trên sẽ được dùng để xây dựng cây quyết định.
Để hiểu rõ hơn về cách thức xây dựng một thuật toán CART đơn giản chúng ta cùng xem qua ví dụ sau, đây cũng là ứng dụng chủ yếu của các thuật toán Decision tree trong lĩnh vực ngân hàng: dự báo khả năng khách hàng mới có thể mang lại rủi ro tín dụng cho tổ chức, dựa trên việc phân loại các khách hàng cũ đã xác định được rủi ro tín dụng theo những đặc điểm cụ thể.
Ví dụ sau đây được tham khảo từ giáo trình “Discovering Knowledge in Data: An introduction to Data mining” của Daniel T.Larose (phần 2).
Giả sử chúng ta có một tập dữ liệu training cho model Decision tree như sau:
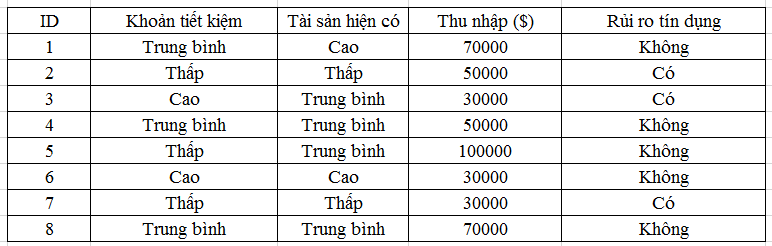
Ngân hàng đã chuyển đổi dữ liệu định lượng ở biến tổng giá trị Khoản tiết kiệm, và tổng giá trị Tài sản hiện có thành dữ liệu định tính với các mức từ Thấp, Trung bình, Cao.
CART chỉ phân được 2 nhánh, một bên trái, một bên phải, nên đầu tiên chúng ta phải xác định biến nào sẽ là root node trong các biến Khoản tiết kiệm, Tài sản hiện có, Thu nhập. Lưu ý biến Rủi ro tín dụng là biến mục tiêu, không được dùng để xét phân nhánh cho cây quyết định mà là kết quả cuối cùng, là điểm dừng cuối cùng của cây quyết định. Vậy dựa trên dữ liệu có được chúng ta có thể có các phân tập dữ liệu thành các phần như sau:
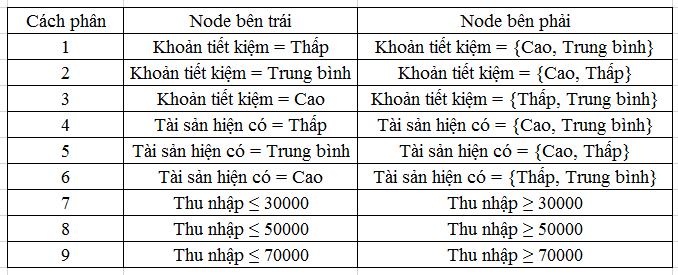
Bây giờ chúng ta sẽ tính xem, các phân nào đem lại giá trị cao nhất được tính từ công thức đã cho phía trên. BigDataUni sẽ tính thử cho bạn cách phân thức 1, các cách phân còn lại các bạn có thể tự tính để kiểm tra với kết quả dưới đây.
Cách phân thứ 1:
Node bên trái, Khoản tiết kiệm thấp, chúng ta xem có 3 khách hàng có khoản tiết kiệm thấp. PL = 3/8 = 0.375.
Node bên phải, Khoản tiết kiệm thuộc cao và trung bình thì chúng ta có 5 khách hàng. PR = 5/8 = 0.625
Tiếp tục, trong 3 khách hàng có khoản tiết kiệm thấp thì có 2 người được phân loại có rủi ro tín dụng, 1 người được phân loại không có rủi ro tín dụng. P (Có rủi ro tín dụng ở node trái) = 2/3 = 0.6667, P (Không có rủi ro tín dụng ở node trái) = 1/3 = 0.3333
Trong 5 khách hàng có khoản tiết kiệm thuộc cao và trung bình, thì có 4 người được phân loại không có rủi ro tín dụng, 1 người được phân loại có rủi ro tín dụng. P (Có rủi ro tín dụng ở node phải) = 1/5 = 0.2, P (Không có rủi ro tín dụng ở node phải) = 4/5 = 0.8
Ráp từng phần vào công thức, vậy cách phân 1 sẽ có giá trị là: Φ = 2*0.375*0.625* [trị tuyệt đối của (0.6667 – 0.2) + trị tuyệt đối của (0.333 – 0.8)] = 0.4378
Chúng ta sau khi tính hết sẽ có kết quả như bảng dưới đây
Lưu ý ký hiệu K trong bảng là tỷ lệ số quan sát trong node trái Không có rủi ro tín dụng, C là Có rủi ro tín dụng.
Theo kết quả có được chúng ta thấy cách phân thứ 4 là có giá trị Goodness of split cao nhất là 0.6248. Vậy theo root node chính là giá trị Tài sản hiện có, phân ra 2 nhánh với node bên trái là Tài sản hiện có = thấp, node bên phải là Tài sản hiện có = {Cao, trung bình}, tại node bên trái, chúng ta phân nhánh tiếp xuống node Rủi ro tín dụng rồi ngắt nhánh vì trong node này có 2 khách hàng có rủi ro tín dụng, đạt 100%, và đây là pure node cần xác định. Vậy sau này khi phân loại rủi ro tín dụng cho khách hàng mới mở khoản vay, nếu khách hàng này có giá trị Tài sản hiện có thấp thì ngân hàng cần xem xét vì họ có khả năng mang lại rủi ro tín dụng
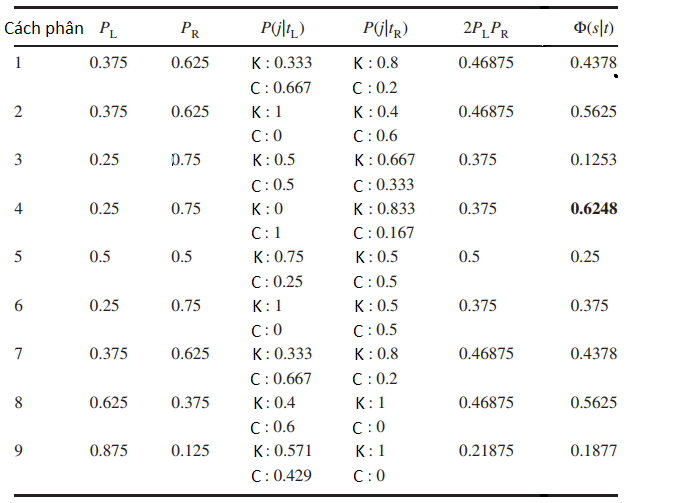
Bảng kết quả xác định cách phân nhánh tối ưu đầu tiên của cây quyết định Chúng ta có thể vẽ cây quyết định với cách phân nhánh đầu tiên có được:

Chúng ta tiếp tục xét tiếp cho 6 khách hàng còn lại ở node bên phải, nguyên nhân là trong số khách hàng này có khách hàng có rủi ro tín dụng và có khách hàng không có rủi ro tín dụng do đó từ đây chúng ta phải phân nhánh tiếp.
Từ bảng các cách phân nhánh mà chúng ta thiết lập ở đầu ví dụ, chúng ta loại có cách phân nhánh thứ 4, và giữ lại các cách phân nhánh còn lại, và bây giờ chúng ta chỉ còn 6 khách hàng để xét.
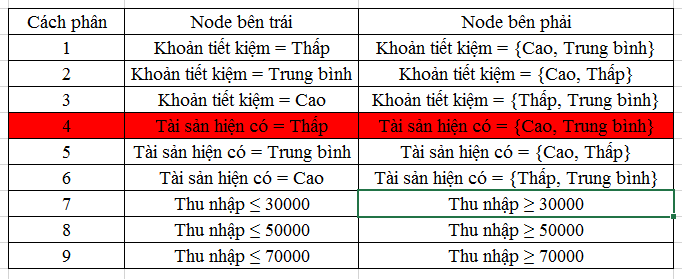
Vậy chúng ta tiếp tục sử dụng công thức trên để tính tiếp Goodness of split cho cách phân 1, 2, 3, 5, 6, 7, 8, 9, lưu ý giá trị sẽ khác so với bảng kết quả đầu tiên do mẫu cần xét bây giờ còn 6. Nếu tính đúng như BigDataUni hướng dẫn, các bạn sẽ có kết quả giống như sau:

Lưu ý ký hiệu K trong bảng là tỷ lệ số quan sát trong node trái Không có rủi ro tín dụng, C là Có rủi ro tín dụng.
Dựa trên bảng trên, chúng ta có thể chọn cách phân thứ 3 hoặc thứ 7 đều được, vì giá trị Goodness đều cao nhất là 0.4444. Ở ví dụ này chúng ta sẽ chọn tiếp cách phân thứ 3 cho lượt phân nhánh tiếp theo. Vậy node bên phải chứa các khách hàng 1, 3, 4, 5, 6, 8 sẽ là node Khoản tiết kiệm, phân nhánh bên trái là khoản tiết kiệm cao có khách hàng 3 và 6, trong số 2 khách hàng này có người có rủi ro tín dụng và có người không nên phải xét tiếp, còn phân nhánh bên phải là khoản tiết kiệm trung bình, thấp là khách hàng 1, 4, 5, 8, tất cả đều không có rủi ro tín dụng, nên node ở nhánh này là pure node, và phân nhánh ngừng ở đây. Các bạn có thể vẽ tiếp CART như sau:
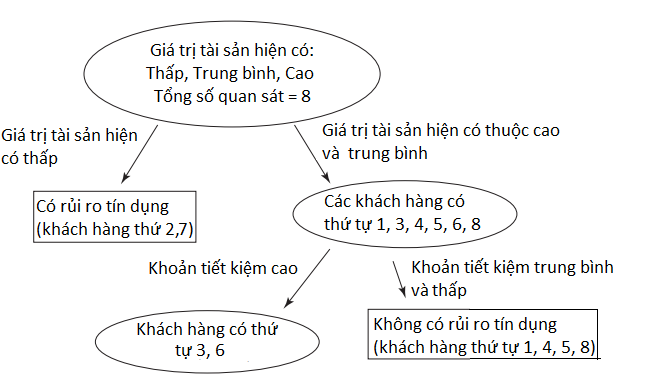
Tiếp tục ở node bên trái chứa khách hàng 3, 6, cả hai đều có cùng khoản tiết kiệm và thu nhập, (các bạn xem lại ở bảng dữ liệu khách hàng ở trên) nên chúng ta phải xét đến giá trị tài sản hiện có, thì thấy, khách hàng thứ 3 với tài sản trung bình thì mang lại rủi ro tín dụng còn khách hàng 6 thì ngược lại.
Sau cùng chúng ta sẽ có một CART hoàn chỉnh như dưới đây
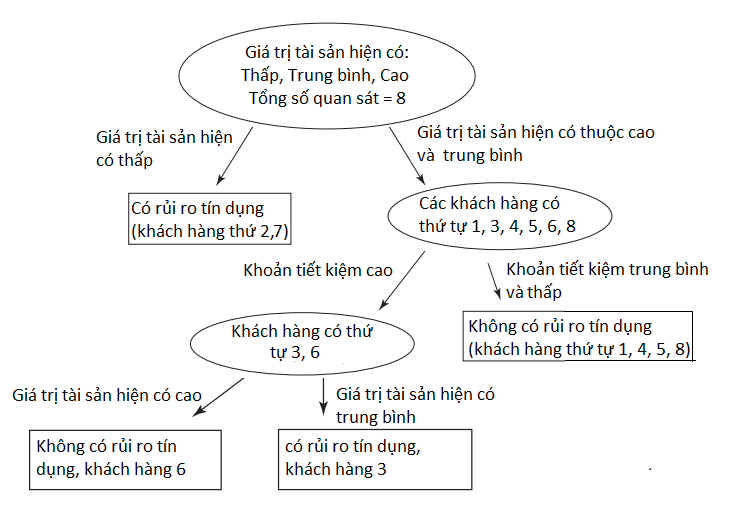
Với thuật toán CART đã xây dựng hoàn chỉnh như trên, ngân hàng đã có thể phân loại khách hàng mới và xem xét liệu họ có mang lại rủi ro tín dụng hay không nếu mở khoản vay cho họ.
Đến đây là kết thúc bài viết về CART cơ bản sử dụng công thức Goodness of split để tính cách phân nhánh tối ưu. Ở bài viết sắp tới chúng tôi sẽ trình bày các bạn về thuật toán CART, C4.5 với công thức Entropy và GINI index, mời các bạn ửng hộ.
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English