Các bài viết trước chúng ta đã tìm hiểu thế nào là Time series, các ứng dụng trong lĩnh vực kinh tế, các chỉ số mô tả đối tượng nghiên cứu trong dữ liệu Time series, phương pháp Moving Average (Trung bình trượt) trong phân tích xu hướng biến động, đặc biệt trong phần 3 vừa rồi BigDataUni đã trình bày đến các bạn cách thức sử dụng Moving Average để phân tích các thành phần trong Time series, và hàm xu thế tuyến tính (Liner trend model) cho mục đích dự báo trong tương lai có điều chỉnh theo yếu tố thời vụ. Phần 4 vừa rồi chúng ta đã tìm hiểu về phương pháp Exponential Smoothing – san bằng hàm mũ dạng đơn giản và Holt – winters cho dữ liệu có hay không có tính xu hướng, và mùa vụ. Bài viết phần 5, phần cuối cùng của chủ đề bài viết đầu tiên về Time series, BigDataUni giới thiệu đến các bạn phương pháp quan trọng khác là ARIMA
Các bạn nào chưa biết gì về Time series có thể tham khảo các bài viết của chúng tôi tại các link dưới đây, chúng tôi sẽ không nói lại nội dung đã trình bày:
Tổng quan về Time series (chuỗi thời gian) (P.1) – Giới thiệu chung, ứng dụng, các thành phần Time series
Tổng quan về Time series (chuỗi thời gian) (P.2) – Các chỉ số mô tả đối tượng trong Time series, giới thiệu về Moving Average
Tổng quan về Time series (chuỗi thời gian) (P.3) – Phân tích các thành phần trong Time series sử dụng Moving Average, và dự báo bằng hàm xu thế
Tổng quan về Time series (chuỗi thời gian) (P.4) – Về phương pháp san bằng hàm mũ Exponential Smoothing

ARIMA – Autoregressive Integrated Moving Average
Mô hình ARIMA được coi là phương pháp quan trọng và được ứng dụng nhiều nhất trong phân tích dãy số thời gian, hoặc có thể xem là “nổi tiếng nhất” khi nhắc đến time series vì các ưu điểm trong hỗ trợ dự báo và sự tinh vi, tính phức tạp của nó. Đặc biệt nó đòi hỏi kinh nghiệm phân tích, mức độ am hiểu về đối tượng nghiên cứu khi lý thuyết hay các nguyên tắc chỉ là một phần chỉ dẫn mà thôi
ARIMA thường không được trình bày một cách chi tiết và đầy đủ nhất trong các giáo trình về Data mining thậm chí không được nói đến trong các sách về lý thuyết thống kê (Statistics) do khối lượng kiến thức liên quan là rất nhiều, nó không đơn giản như moving average, trend model hay exponential smoothing. Nếu muốn tìm kiếm tất cả lý thuyết liên quan đến mô hình ARIMA, các bạn phải search các tài liệu chuyên về mảng time series.
Do đó, chỉ vỏn vẹn trong bài viết này chúng tôi không thể trình bày quá sâu về ARIMA, mà sẽ tập trung vào những thành phần cơ bản, quan trọng, dễ hiểu trong ARIMA nhưng chưa thể ứng dụng vào thực tế, mong các bạn thông cảm! Chúng tôi khuyến khích các bạn tham khảo thêm nhiều tài liệu khác để biết thêm nhiều rules, nhiều phát hiện hay trong mô hình ARIMA.
Với những kiến thức cơ bản trong bài viết này, BigDataUni chỉ mong các bạn sẽ có kiến thức được coi là nền tảng về ARIMA để hỗ trợ nghiên cứu sâu hơn trong tương lai.
Vậy ARIMA là gì? Chúng ta khoan hãy nói đến cái tên, và các thành phần bên trong nó mà trước tiên cùng đi vào giải thích chung nhất về ARIMA.
Mô hình ARIMA là một công cụ vô cùng “mạnh mẽ”, một dạng mô hình/ phương pháp thống kê hỗ trợ phân tích và dự báo cho dữ liệu chuỗi thời gian.
Time series được chia thành 2 loại chính là Univariate Time Series Forecasting – dự báo chuỗi thời gian đơn biến, tức chỉ sử dụng dữ liệu/ giá trị lịch sử trước đó để dự báo trong tương lai. Và Multi -Variate Time Series Forecasting – sử dụng các biến số khác bên cạnh time series data để dự báo trong tương lai.
ARIMA gần như thuộc loại thứ nhất, sử dụng các thông tin/ dữ kiện lịch sử để đưa ra dự báo hay nói cách khác ARIMA hoạt động dựa trên giả định là các thông tin/ dữ kiện lịch sử có thể được sử dụng “một mình” để dự báo các giá trị trong tương lai.
ARIMA ‘giải thích’ một dãy số thời gian nhất định dựa trên các giá trị trong quá khứ của chính nó, bao gồm cả độ trễ và lỗi dự báo bị trễ, để có thể sử dụng phương trình xây dựng mô hình dự báo các giá trị trong tương lai. Ban đầu nghe có vẻ khó hiểu, khi đi vào chi tiết công thức chúng tôi sẽ giải thích kỹ hơn.
ARIMA cũng giống các phương pháp trong Time series cho phép chúng ta xác định sự tăng trưởng/ đi xuống của đối tượng nghiên cứu, tốc độ thay đổi ra sao, và các yếu tố nhiễu/ ngẫu nhiên tác động vào đối tượng qua các mốc thời gian,… và nhiều hơn thế.
ARIMA hoạt động giống một máy ép nước mía, và các cây mía chính là dữ liệu Time series. Máy ép cần phải thực hiện ép mía nhiều lần thì mới lấy được tối đa nước mía ngọt, phần bã mía không thể sử dụng được nữa. Tương tự ARIMA sẽ trích xuất tối đa các thông tin hữu ích từ dữ liệu Time series, cho đến khi còn phần dư dữ liệu không thể trích xuất thêm thông tin được nữa.
ARIMA gồm 3 thành phần chính Autoregressive, Intergrated, và Moving Average
Autoregressive (AR)
Autoregressive hay Autoregression – chuỗi tự hồi quy.
Chúng ta sử dụng hàm xu thế tuyến tính áp dụng dự báo dữ liệu Time series mà ở đó thể hiện tính xu hướng hay thời vụ theo thời gian, có mối quan hệ giữa những giá trị của đối tượng nghiên cứu với các mốc thời gian.
Tuy nhiên trong dữ liệu dãy số thời gian sẽ có một mối quan hệ tìm ẩn nào đó mà chúng ta không biết được khi sự am hiểu về đối tượng nghiên cứu bị hạn chế. Ví dụ như có mối quan hệ tương quan giữa các giá trị trong quá khứ với giá trị dự báo ở tương lai. Mối quan hệ tự tương quan như vậy được gọi là Autocorrelation.
Gọi là Autocorrelation “chuỗi tự động tương quan” nghĩa là chính các giá trị dữ liệu có mối quan hệ với chính nó. Để phân tích mối quan hệ đặc biệt này chúng ta sẽ sử dụng phương pháp “chuỗi giá trị trễ” hay “lagged series”, tức giá trị ở mốc thời gian trước sẽ được dời lên n bậc. Ví dụ dời lên 1 bậc, và 2 bậc theo ví dụ Mc.Donald’s dưới đây:
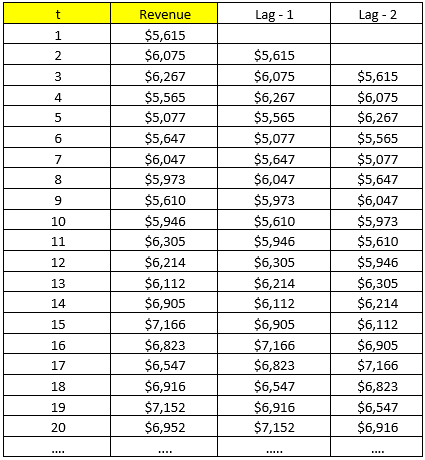
Hệ số tự tương quan sẽ được tính giữa chuỗi giá trị gốc và giá trị trễ, công thức tổng quan như sau:
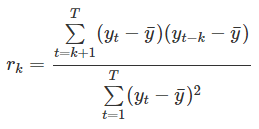
K là độ trễ bậc k, còn T là độ dài khoảng thời gian của time series. Công thức trên còn gọi là công thức ACF (Autocorrelation function)
Chúng ta sẽ tính thử cho ví dụ Mc. Donald’s. Dưới đây là kết quả:

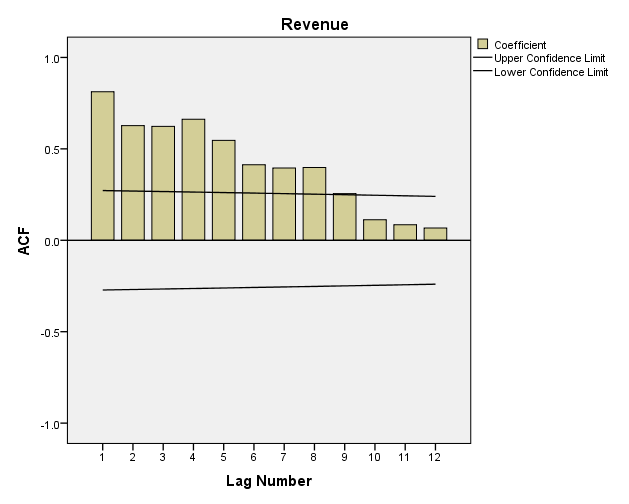
Đối với hệ số tự tương quan của ACF, chúng ta sẽ thực hiện kiểm định bằng công thức kiểm định Chi-square Box-ljung như sau:
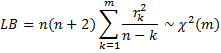
n là số giá trị trong time series, k là độ trễ, bậc tự do df của kiểm định sẽ bằng k. Phát biểu như sau nếu giá trị p-value tính được < α, thì tối thiểu một trong các hệ số tự tương quan ứng với các độ trễ k ≤ m sẽ khác 0. Kết quả từ SPSS:
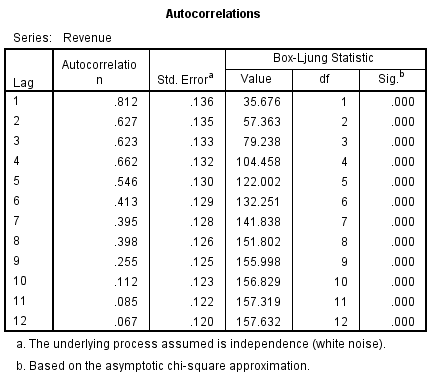
Ví dụ Sig của lag-4, tức p-value < 0.05, vậy hệ số tương quan ACF(k) sẽ khác 0, với ít nhất một k ≤ 4 (từ R1 đến R4, sẽ có ít nhất 1 giá trị khác 0).
Kết quả kiểm định cho thấy các giá trị quá khứ trước đó có mối quan hệ với các giá trị trong tương lai, và có ý nghĩa phân tích, xét trong ví dụ Mc. Donald’s.
Ngoài ra, nhìn lại đồ thị, các đoạn thẳng confidence limit sẽ tạo thành miền tin cậy cho các hệ số tương quan đạt giá trị bằng 0, nếu các hệ số tương quan ACF nằm trong vùng này, sẽ không có ý nghĩa phân tích.
Nếu tất cả đều nằm trong vùng tin cậy, thì trường hợp có thể này gọi là White noise, theo thuật ngữ của các chuyên gia, nghĩa là dữ liệu không có biểu hiện của Autocorrelation, các hệ số tương quan càng gần giá trị 0, suy ra không có mối quan hệ giữa chính các giá trị. Ngoài ra White noise xảy ra khi trung bình hay mean của Time series = 0, và phương sai bằng nhau ở tất cả các mốc thời gian.
Khi dữ liệu bị White noise, tức tất cả các giá trị được hiểu là xảy ra ngẫu nhiên, thì chúng ta không thể đưa ra dự báo cho đối tượng nghiên cứu trong Time series. Mặt khác, khi xây dựng các mô hình dự báo, các sai số dự báo cần phải ngẫu nhiên hoàn toàn, nếu không phải tức mô hình không hiệu quả.
Confidence limit được tính theo công thức ±2 (T)1/2 với T là độ dài time series. Ở ví dụ này, T = 51, ±2 (51)1/2 = ± 0.28. Upper confidence limit sẽ cách trục hoành khoảng giá trị 0.28, tương tự lower confidence limit sẽ là -0.28.
Chúng tôi nói kỹ phần này vì đây là cơ sở để chọn độ trễ bậc k phù hợp cho mô hình ARIMA.
ACF không chỉ được dùng cho ARIMA mà nó còn được dùng để đánh giá tính biến động và xu hướng trong dữ liệu Time series. Dưới đây là một số lưu ý:
- Hệ số tự tương quan tại Lag-1 có giá trị > 0, và cách xa 0, thể hiện các giá trị liên tiếp nhau cùng di chuyển về một hướng, thể hiện xu hướng tuyến tính mạnh. Trường hợp doanh thu Mc.Donald’s là ví dụ cụ thể.
- Hệ số tự tương quan tại Lag-1 < 0, biểu hiện trong tập dữ liệu, các giá trị lớn theo sau đó là sẽ các giá trị nhỏ hoặc ngược lại.
- Hệ số tự tương quan tại Lag – k với k > 1, và các hệ số tại các bội số của nó Lag – (2k), Lag – (3k) có giá trị lớn thì khả năng cao dữ liệu Time series có tính chu kỳ hay thời vụ xét theo mốc thời gian thu thập dữ liệu.
Ví dụ hệ số tự tương quan R4 tại độ trễ bậc 4 có giá trị cao hơn các hệ số tự tương quan còn lại, doanh thu McDonald’s có biến động thời vụ, doanh thu đạt cao nhất hay thấp nhất sẽ cách nhau 4 quý, như trong mẫu dữ liệu hầu hết doanh thu quý 3 năm này và quý 3 năm sau đều cao nhất.
Ngoài ra nhìn vào Correlogram chúng ta cũng có thể đánh giá chung được tính xu hướng. Cụ thể khi dữ liệu có tính xu hướng thì các giá trị hệ số tự tương quan tại các bậc k nhỏ hơn sẽ lớn hơn 0, cách xa giá trị 0, và giảm dần khi bậc k lớn dần. Như ví dụ trên lag-1 đến lag-4 có hệ số lớn, từ lag-5 trở đi có dấu hiệu hệ số giảm, doanh thu của McDonald’s có tính xu hướng.
Để đánh giá một cách chính xác về Autocorrelation, từ tổng quan đến chi tiết và hỗ trợ cho việc dự báo, thì chúng sẽ sử dụng mô hình tự hồi quy Autogressive model, công thức như sau:
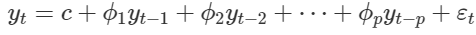
Công thức gần giống với hồi quy tuyến tính đa biến nhưng khác chính là các biến đầu vào là các giá trị quá khứ, là các chuỗi trễ.
Mô hình viết tắt là AR (p) với p gọi là tham số trễ, hay độ trễ của AR. Ví dụ nếu AR(2) thì biến đầu vào sẽ chỉ bao gồm 2 chuối trễ là lag-1 (Yt-1) và lag-2 (Yt-2).
Việc xác định p là bước quan trọng nhất. Tuy nhiên lưu ý quan trọng, phương pháp ACF không được dùng để xác định p nhé!
Các hệ số Ø chính là các tham số hồi quy, c là constant, hằng số của mô hình hồi quy, ε là sai số dự báo, biểu hiện của các yếu tố ngẫu nhiên không thể kiểm soát.
Ví dụ cho dữ liệu McDonald’s, giả sử chúng ta nghi ngờ rằng có thể các dữ liệu quá khứ có mối quan hệ với dữ liệu dự báo. Chúng ta chọn độ trễ = 3 để làm ví dụ.
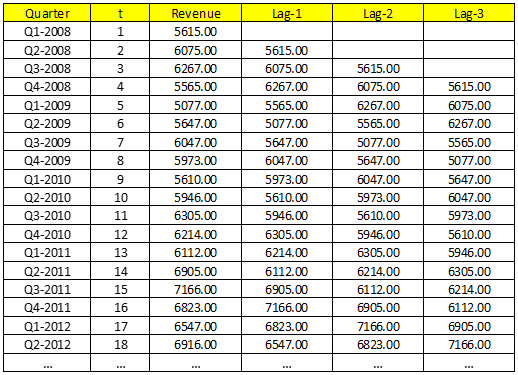
Chúng ta sử dụng dữ liệu từ Q4-2008 trở xuống để đưa vào mô hình
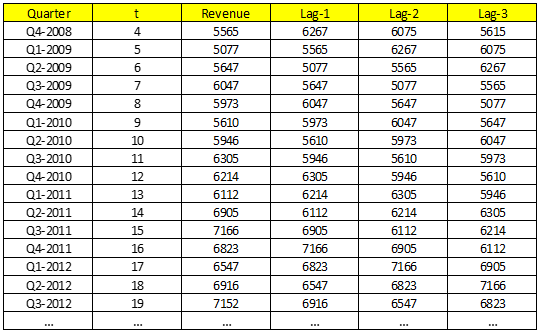
Revenue là biến mục tiêu, các lag-1, lag-2, lag-3 là các biến độc lập của Autoregressive model. Như vậy chúng ta có mô hình:
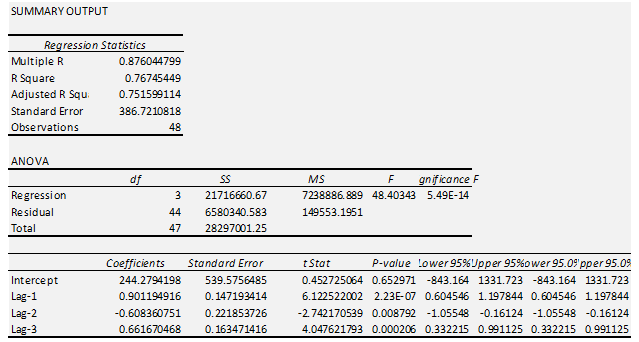
P-value kiểm định t, của 3 biến lag-1, lag-2, lag-3 đều có P-value < 0.05, nên có thể kết luận các biến này có tác động lên kết quả dự báo doanh thu của McDonald’s.
AR (3):
Yt^ = 244.28 + 0.9*Yt-1 – 0.6*Yt-2 + 0.66*Yt-3
Dự báo thử Y52 = 244.28 + 0.9*Y51 – 0.6*Y50 + 0.66*Y49 = 4167.74
Nếu các bạn tính lại thử cho tất cả các mốc thời gian, sử dụng phương trình trên, sau đó tính sai số bình phương, rồi trung bình sai số bình phương MSE, kết quả thu được MSE = 215831. So sánh với các phương pháp ở những bài viết trước vẫn còn chưa hiệu quả bằng phương pháp Exponential Smoothing. Các bạn có thể xem lại các bài viết trước của chúng tôi để rõ hơn.
Kết quả dự báo kém chính xác có thể do việc chọn lựa độ trễ không phù hợp, các biến đầu vào chưa hợp lý.
Để xác định độ trễ phù hợp, p trong AR(P) các chuyên gia thường sử dụng một công cụ khác chính là PCF (Partial Autocorrelation Function)
Giải thích một cách dễ hiểu về PCF. Ví dụ một giám đốc kinh doanh tại McDonald’s cho rằng thông tin doanh thu quý thứ 1 sẽ hỗ trợ dự báo doanh thu cho quý thứ 3 hiện tại. Theo cách nói của vị giám đốc này thì có 2 cách nghĩ. Gọi Yt-2 (Quý 1), Yt-1 (Quý 2), Yt (Quý 3)
- Yt-2 => Yt-1 => Yt
- Yt-2 => Yt
Thứ nhất, doanh thu tại quý thứ 1, tác động lên doanh thu ở quý thứ 3 thông qua quý thứ 2, tức quý thứ 2 có sức ảnh hưởng lên việc dự báo ở quý thứ 3. Mối tương quan này gọi là gián tiếp – Indirect Correlation. Thứ hai, doanh thu quý thứ 1 tác động trực tiếp lên dự báo doanh thu quý thứ 3 mà không qua quý thứ 2 trung gian. Mối tương quan này gọi là trực tiếp – Direct Correlation. Hai mối tương quan này tạo thành ACF như chúng ta đã biết ở trên.
PCF hay PACF tập trung tìm hiểu mối quan hệ trực tiếp giữa quan sát hiện tại với các quan sát trong quá khứ, mà bỏ qua các mối quan hệ trung gian. Lý do, nếu chúng ta chỉ muốn phân tích sự liên hệ giữa 2 biến, 2 đối tượng quan sát, giá trị ở mốc thời gian t hiện tại với giá trị ở mốc t – k nào đó trong quá khứ mà không quan tâm đến các dữ liệu còn lại, thì PCF nên được sử dụng.
Khi các tác động gián tiếp xuất hiện, việc đánh giá mối tương quan có thể không chính xác. Cụ thể ví dụ, thực chất doanh thu quý thứ 1 có quan hệ với doanh thu quý thứ 3 là do doanh thu quý thứ 2 gây nên do những yếu tố nào đó chúng ta chưa biết.
Quay lại với mô hình AR:
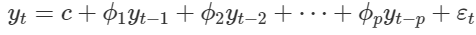
Như vậy để tìm được các biến lag – k thích hợp nhất, các hệ số hồi quy chính xác nhất, thể hiện mối quan hệ trực tiếp giữa từng biến lag – k với biến mục tiêu Yt, thì chúng ta cần sử dụng PACF.
Công thức tổng quan:
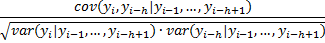
h là giá trị hay quan sát ở mốc thời gian thứ h trong quá khứ, i là giá trị hay quan sát ở mốc thời gian thứ i ở hiện tại hay mốc thời gian đang xét đến.
Quay trở lại với ví dụ Mc.Donald’s
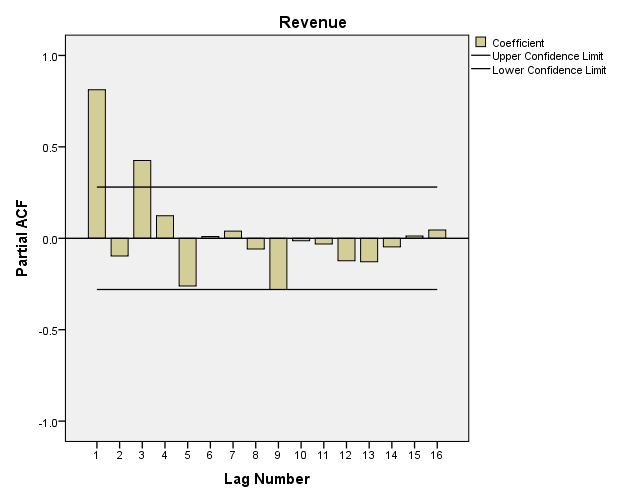
Về Upper và Lower Confidence Limit giải thích tương tự như trên ACF nên chúng tôi không nói lại ở đây. Như vậy để chọn ra độ trễ p phù hợp cho AR(p), chúng ta xem có bao nhiêu lag-k có hệ số tương quan PCF nằm ngoài vùng tin cậy. Ở đây chúng ta thấy có Lag-1 và Lag-3 là phù hợp.
Chúng ta chọn p = 3, AR(3).
Yt = c + Ø1*Yt-1 + Ø2*Yt-2 + Ø3*Yt-3 + et
Các bạn lưu ý p ở đây chính là bậc trễ tối đa có trong phần AR trong mô hình ARIMA. P = 3 nghĩa là phần AR sẽ có 3 chuỗi trễ là các biến đầu vào Yt-1, Yt-2 và Yt-3. Cách chọn p thông dụng chính là xem tại lag-k nào có PACF nằm ngoài vùng tin cậy và sau đó không có lag-k nào nằm bên ngoài vùng tin cậy. Ở đây chúng ta thấy sau lag-3 thì không có lag-k nào khác có PACF vượt qua vùng tin cậy, nên ngừng ở 3.
Tuy nhiên nếu xét riêng mô hình AR mà thôi thì khả năng chúng ta sẽ loại bỏ Yt–2 do lag-2 nằm trong vùng tin cậy. Mặc dù vậy khi xem qua kết quả mô hình AR ở ví dụ trên chúng ta thấy p-value lag- 2 = 0.008 < 0.05 nên suy ra vẫn có ý nghĩa phân tích nên có thể giữ lại.
- Moving Average (MA)
Ở các bài viết trước chúng ta sử dụng phương pháp trung bình trượt để phân tích xu hướng biến động, các thành phần trong Time series cũng như loại bỏ tính thời vụ của dãy số và xây dựng hàm xu thế tuyến tính hỗ trợ dự báo.
Mục đích đầu tiên và sau cùng của việc sử dụng trung bình trượt Moving Average chính là loại bỏ các yếu tố ngẫu nhiên, yếu tố nhiễu, bất thường không kiểm soát, có thể tác động lên kết quả dự báo giúp quy trình dự báo trở nên dễ dàng và hiệu quả hơn.
Trong mô hình ARIMA, MA đóng vai trò như là công cụ sẽ truy xuất các thông tin về sai số dự báo ở các mốc thời điểm trong quá khứ sẽ ảnh hưởng như thế nào đến sai số dự báo ở mốc thời gian trong tương lai.
Chính vì thế nó khác với phương pháp trung bình trượt thông thường chúng ta sử dụng ở các bài viết trước.
Để hiểu rõ hơn chúng ta cùng đi qua ví dụ sau:
Giả sử bộ phận lãnh đạo của Mc.Donald’s mong muốn trung bình doanh thu mỗi tháng phải là 1.5 tỷ USD, 1500 (triệu USD), bộ phận bán hàng sẽ phải đưa ra dự báo về doanh thu để xây dựng các chiến lược hành động phù hợp, dựa trên các sai số so với 1500, thí dụ, họ nhận định doanh thu thấp hơn 1500 là 1200, sai số âm là 300, họ phải tìm ra cách thúc đẩy năng suất hơn nữa để đạt được thêm một khoảng doanh thu ít nhất là 300.
Nếu không có yếu tố ngẫu nhiên nào xảy ra thì bộ phận bán hàng chắc chắn đảm bảo được yêu cầu về doanh thu, tuy nhiên thực tế không phải như vậy. Nên mục đích là phải dự báo được sai số ngẫu nhiên, viết tắc ε – error.
Thông qua nghiên cứu, họ thấy được sai số từ việc dự báo doanh thu tháng trước có thể dự báo được cho doanh thu tháng hiện tại
Ví dụ: Ft = μ + Ө1*εt-1
Giả sử sai số dự báo tháng này sẽ bằng 0.75 sai số dự báo tháng trước.
Ft = 1500 + 0.75*300 = 1725
Tuy nhiên vì theo yêu cầu bài toán, μ – giá trị trung bình, giữ nguyên không thay đổi theo thời gian, mà như các bạn đã biết, ở phương pháp trung bình trượt thì các giá trị trung bình sẽ thay đổi theo mốc thời gian.
Do đó để μ – giá trị trung bình không thay đổi theo thời gian thì dữ liệu Time series phải có tính “Stationarity” tức có tính dừng/ không thay đổi/ không tăng giảm theo thời gian hay nói cách khác các giá trị không phụ thuộc vào các mốc thời gian, yếu tố xu hướng và thời vụ đã bị loại bỏ. Chúng tôi sẽ nói cụ thể ở phần sau.
Khi dữ liệu được đảm bảo tính dừng, thì nếu giá trị trung bình biến động, suy ra nó hoàn toàn do yếu tố ngẫu nhiên gây nên. Các sai số εt sẽ có trung bình hay kỳ vọng = 0, và phương sai không đổi. (με = 0, σε không đổi) => lúc này các giá trị dự báo sẽ có trung bình bằng μ hay các điểm dữ liệu dao động xung quanh một đường trung tâm chính là đường trung bình μ.
Ví dụ như hình dưới đây, đường thẳng từ giá 0 trục hoành chính là đường trung tâm.
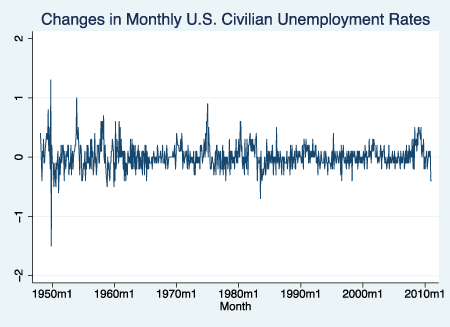
Công thức tổng quát mô hình MA được xây dựng dựa trên phương pháp hồi quy tuyến tính đa biến đơn giản như sau.
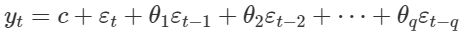
Công thức dự báo thì chúng ta loại bỏ εt ra do chúng ta không thể xác định được các yếu tố ngẫu nhiên không kiểm soát. C là hằng số, giống μ, các hệ số Ө chính là hệ số hồi quy.
Chúng ta đã có phần thứ 2 của ARIMA chính là MA (q) với q là bậc trễ mà tại đó các sai số ở những mốc thời gian t ≤ q có mối liên hệ với sai số của biến mục tiêu.
Nếu mô hình AR sử dụng PACF để xác định p, thì MA sẽ sử dụng ACF để tìm q.
Để lý giải nguyên nhân sử dụng ACF thì sẽ phải sử dụng công thức toán học mà cụ thể là công thức tính hệ số tương quan. Nó khá phức tạp, do bài viết có hạn nên chúng tôi sẽ không trình bày ở đây.
Nếu dữ liệu Time series có giá trị tương quan ACF tại lag-k khác 0 hay có ý nghĩa phân tích (Significant) mà không phải tại các lag-t với t > k thì hệ số q trong MA sẽ bằng với k.
Ví dụ chúng ta quay lại với ACF tính cho doanh thu của Mc.Donald’s
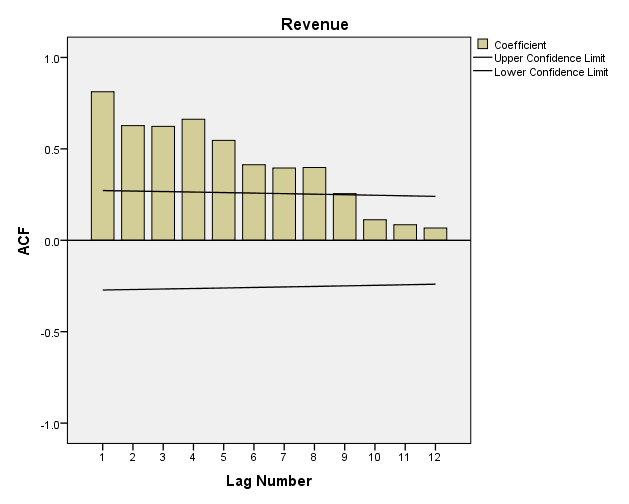
Từ lag-1 đến lag-8 có giá trị ACF nằm ngoài miền tiên cậy, suy ra có mối quan hệ tương quan với đối tượng nghiên cứu. Theo quy tắc, chúng ta sẽ chọn k = 8, tuy nhiên, nếu k quá lớn sẽ khiến cho mô hình có quá nhiều biến dự báo, do đó các chuyên gia thường chọn k hay q = 5 là tối đa.
Lưu ý trong thực tế, có các quy tắc kết hợp PCF, ACF trong việc xác định p, q cho AR và MA, chúng tôi tách biệt ra để giải thích cho các bạn rõ hơn và tránh nhầm lẫn nên các cách thức trình bày ở trên chỉ mang tính tham khảo. Các quy tắc trong ARIMA chúng tôi chưa thể đề cập trong bài viết này, hi vọng ở chủ đề bài viết khác về Time series trong tương lai chúng tôi có dịp sẽ gửi đến các bạn.
- Stationarity/ Differencing
Như vậy khi có mô hình AR, và mô hình MA chúng ta tạm thời sẽ có công thức tổng quan cho mô hình ARMA đầu tiên bằng cách cộng 2 phần công thức dưới đây lại với nhau:
AR(p)
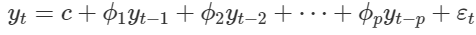
MA(q)
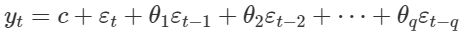
Chúng ta còn phần I – Integrated. Nhiều bạn sẽ hiểu rằng AR và MA được tích hợp với nhau tạo thành ARIMA. Tuy nhiên không phải như vậy! Chúng ta phải chuyển đổi dữ liệu Time seris không có tính dừng sang dữ liệu có tính dừng.
Dữ liệu Stationarity hay dữ liệu có tính dừng là dữ liệu Time series mà ở đó các giá trị quan sát hoàn toàn không phụ thuộc vào các mốc thời gian, không có yếu tố xu hướng, và không có yếu tố thời vụ. Ngoài ra dữ liệu Stationarity sẽ không thể dự báo được trong dài hạn, do nó biến động hoàn toàn theo yếu tố ngẫu nhiên – White noise (mean = 0 và không đổi) – một dạng Stationarity. Dữ liệu Stationarity đặc trưng với trung bình Mean và phương sai không đổi theo thời gian hay ACF sẽ có các lag-k giảm xuống mức 0 khá nhanh theo thời gian (hoặc ở một số trường hợp, các lag-k nằm trong vùng tin cậy của ACF thì khả năng cao dữ liệu đã có tính dừng)
Ví dụ chúng ta có 2 đồ thị như sau:
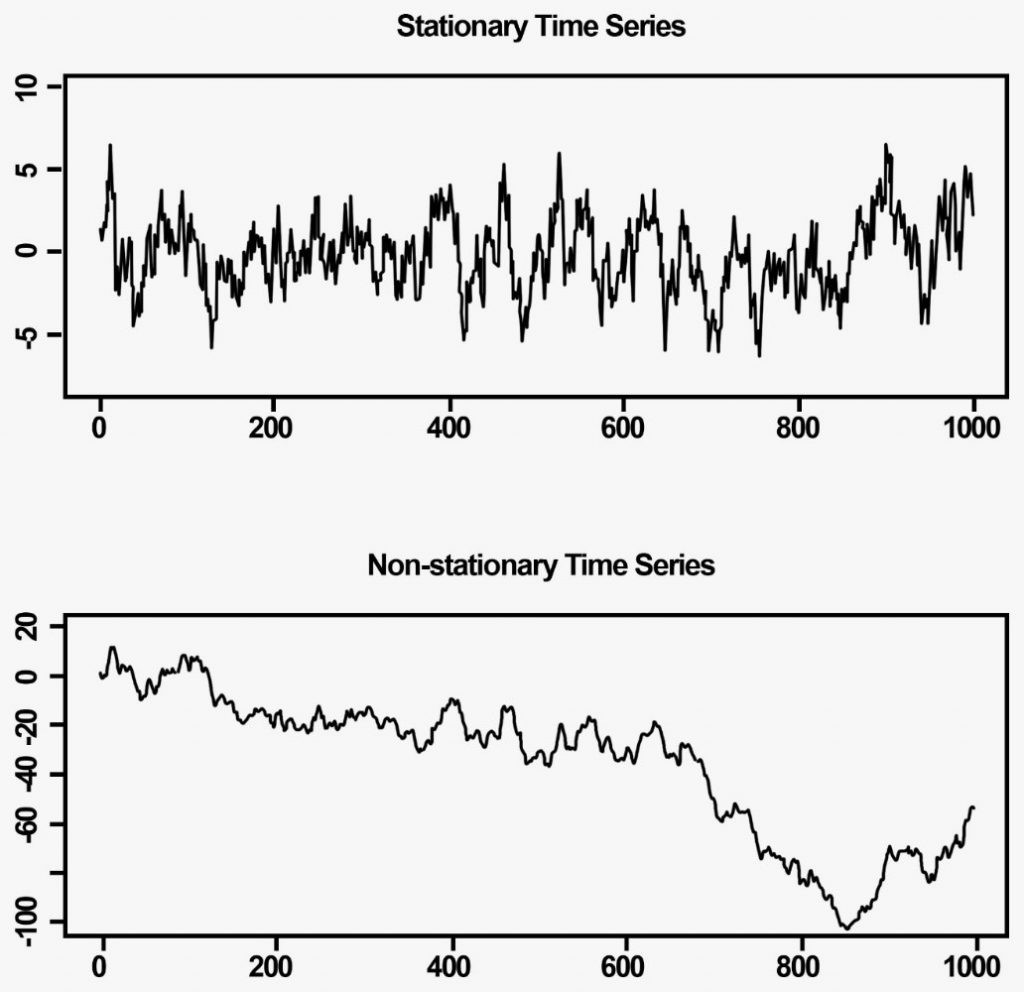
Dữ liệu Stationarity sẽ không cho thấy được tính xu hướng, và tính thời vụ không rõ ràng, khi dữ liệu tăng giảm không theo quy luật theo thời gian, và chúng dao động xung quanh một trục giữa (ví dụ từ 0 vẽ 1 đường thẳng nằm ngang các bạn sẽ thấy được), tức thể hiện trung bình sẽ không thay đổi.
Cách biến dữ liệu Time series từ không có tính dừng sang có tính dừng chúng ta sẽ dùng một trong các công thức phổ biến nhất là Differencing hay còn gọi phương pháp tính Sai phân.
Differencing tính toán sự chênh lệch giữa các giá trị quan sát nằm ở các mốc thời gian liên tiếp nhau. Tương tự như AR, và MA chúng ta cũng xác định mức hay bậc được gọi là d cho Differencing.
+ d = 0. Không có tính sai phân, dữ liệu đã có tính dừng.
Yt’ = Yt
+ d = 1. Sai phân bậc 1
Yt’ = Yt – Yt-1
+ Nếu dữ liệu chưa có tính dừng chúng ta làm tiếp bậc thứ 2. d = 2
Yt’’= Yt’ – Yt-1’ = (Yt – Yt-1) – (Yt-1 – Yt-2) = Yt – 2Yt-1 + Yt-2
Chúng ta sẽ tiếp tục sai phân bậc tiếp theo nếu dữ liệu chưa đạt Stationarity. Tuy nhiên d không được quá 5, tức 0 < d < 5, tốt hơn chỉ tối đa là 3, thông dụng nhất chỉ là 2. Nếu hơn tức dữ liệu của chúng ta có vấn đề, cần xem xét kỹ các phương pháp phân tích khác trong Time series, vì lúc này có thể ARIMA sẽ không còn phù hợp
Vậy bằng cách nào để kiểm tra dữ liệu sau khi qua các bậc sai phân?
Để kiểm tra chúng ta có thể sử dụng các đặc trưng của dữ liệu Stationarity ở trên, kết hợp nhìn vào đồ thị Time series xác định có sự biến động theo xu hướng hay thời vụ không. Sau cùng chúng ta sẽ sử dụng các công thức kiểm định thống kê như Dickey-Fuller (Augmented), Phillips-Perron & KPSS tests. Cách triển khai kiểm định cũng như công thức khá phức tạp, may mắn là các phần mềm thống kê hay Data mining đều có tích hợp sẵn các dạng test này nên các bạn cũng không cần quá lo lắng, chỉ cần nhớ quy tắc đặt giả thuyết và bác bỏ như sau:
- Với Dickey-Fuller, và Phillips-Perron thì H0: Dữ liệu không có Stationarity và H1 là ngược lại. Các bạn chỉ cần xem p-value có lớn hơn mức ý nghĩa, giả sử mặc định là 0.05, nếu có, bác bỏ H0 và kết luận dữ liệu có Stationarity và ngược lại. Hoặc dựa trên giá trị kiểm định Tau, so sánh với Tau trai bảng hay còn gọi là Critical Tau, nếu Tau kiểm định < Tau tra bảng, bác bỏ H0 kết luận tương tự ở trên và ngược lại.
- Riêng trường hợp KPSS, ta sẽ đặt giả thuyết ngược lại, H0: Dữ liệu có Stationarity và H1: Dữ liệu không có Stationarity. Các bạn chỉ cần xem p-value có lớn hơn mức ý nghĩa, giả sử mặc định là 0.05, nếu có, bác bỏ H0 và kết luận dữ liệu không có Stationarity và ngược lại. Hoặc dựa trên giá trị kiểm định, so sánh giá trị tra bảng KPSS, nếu lớn hơn thì bác bỏ H0 kết luận tương tự
Như vậy chúng ta đã tìm hiểu 3 thành phần quan trọng tạo thành mô hình ARIMA là AR(p), MA (q) và I (Differencing – d)
Đây là công thức tổng quát ARIMA (p, d, q)
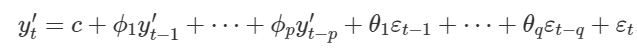
Chúng ta dùng Yt’ thay vì Yt là thể hiện dữ liệu đã qua Sai phân.
Ngoài ra có cách viết thứ 2, chính là sử dụng Backshift – B

Còn sai phân Differencing
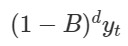
Công thức tổng quát ARIMA(p, d, q) theo Backshift – B
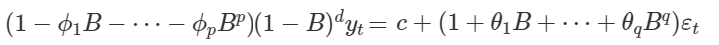
Lý do sử dụng Backshift là tinh gọn công thức, và thể hiện phần sai phân rõ hơn công thức đầu tiên. Như vậy việc cần làm bây giờ là xác định p, d, q để có một mô hình ARIMA phù hợp nhất để dự báo.
Để so sánh các mô hình ARIMA để chọn ra p, d, q tối ưu nhất, thì có một chỉ số đánh giá phổ biến nhất chính là AIC (Akaike’s Information Criterion) Nó đánh giá chất lượng của các mô hình ARIMA có p, d, q khác nhau áp dụng trên cùng 1 tập dữ liệu. AIC đo lường lượng thông tin bị mất do dự báo sai của các mô hình, dựa trên nguyên lý Maximum Likelihood Estimation (MLE). Mô hình nào có AIC càng thấp thì càng tốt. Công thức AIC
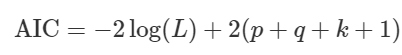
Khi c = 0, thì k = 0, nếu c khác 0, thì k = 1. (p + q + k + 1) là tổng số tham số ước tính sẽ có trong mô hình. Ngoài ra còn có hệ số AICc là hệ số điều chỉnh từ AIC
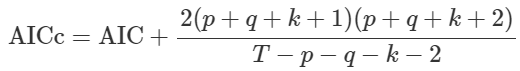
Và hệ số BIC (Bayesian Information Criterion)
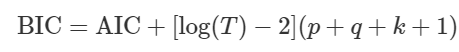
Các hệ số trên càng giảm, thì mô hình càng hiệu quả.
Và để dự báo Yt + 1 chúng ta phải xác định được các hệ số và chuyển đổi công thức phù hợp ví dụ:ARIMA (3, 1, 1)
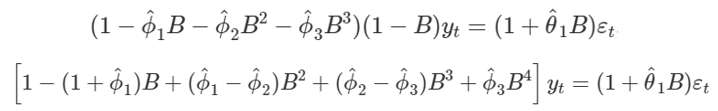
Áp dụng công thức Backshift để chuyển ngược lại Yt-k
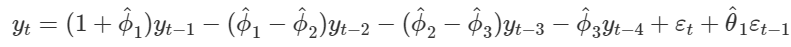
Chúng ta t bằng T + 1
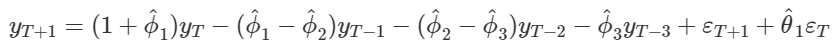
Vì εt + 1 chưa biết nên chúng ta loại bỏ ra để có được phương trình dự báo hoàn chỉnh
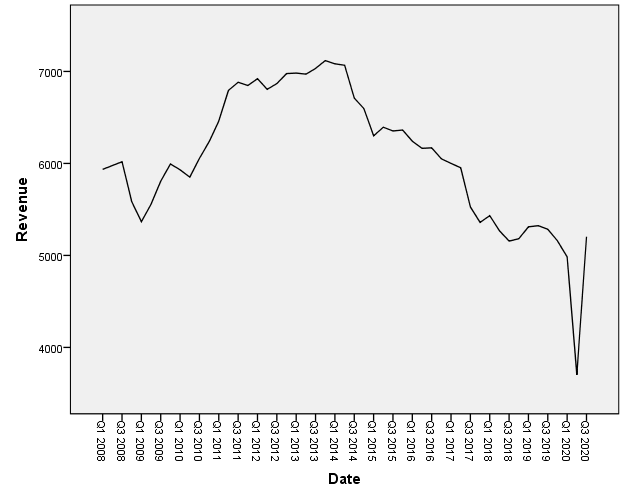
Chúng ta cùng quay lại với ví dụ McDonald’s. Dữ liệu ban đầu được mô tả qua đồ thị sau. Các bạn xem lại các bài viết trước nếu chưa rõ ví dụ
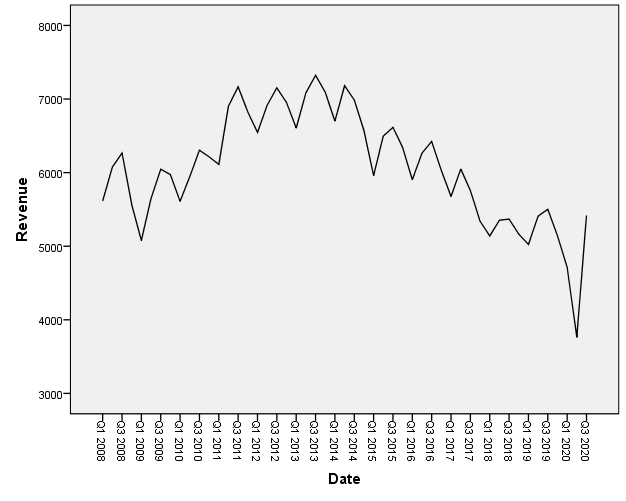
Vì dữ liệu yêu cầu không có tính thời vụ, và chúng ta chưa tìm hiểu về SARIMA – phương pháp ARIMA áp dụng cho dữ liệu có thời vụ. Các bạn có thể tham khảo SARIMA ở các tài liệu khác, chúng tôi không đề cập trong bài viết lần này. Nếu có cơ hội chúng tôi sẽ giới thiệu ở chuỗi các bài viết khác về Time series.
Các bài xem lại bài viết phần 3, để hiểu về cách loại bỏ yếu tố thời vụ trong dữ liệu Time series.
Dữ liệu doanh thu Mc.Donald’s sau khi loại bỏ yếu tố thời vụ:
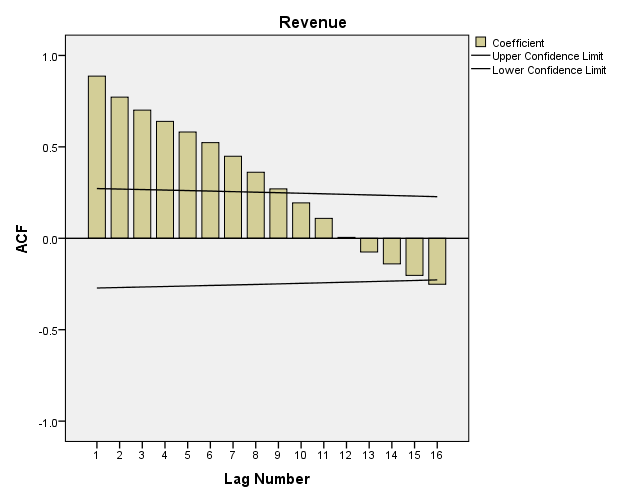
Đồ thị ACF dưới đây cho thấy các lag-k với k ≤ 9 có hệ số tương quan ACF nằm ngoài vùng tin cậy nên có ý nghĩa trong thể hiện mối quan hệ giữa chúng với biến mục tiêu đối tượng nghiên cứu nên dữ liệu này không phải là Stationarity.
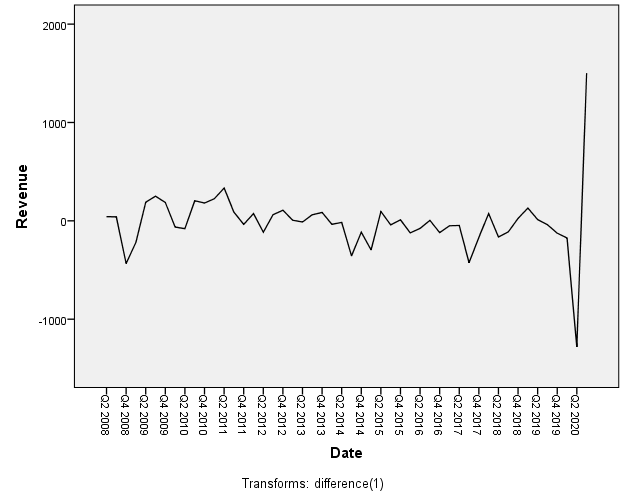
Chúng ta thực hiện sai phân bậc 1, dữ liệu sau khi sai phân
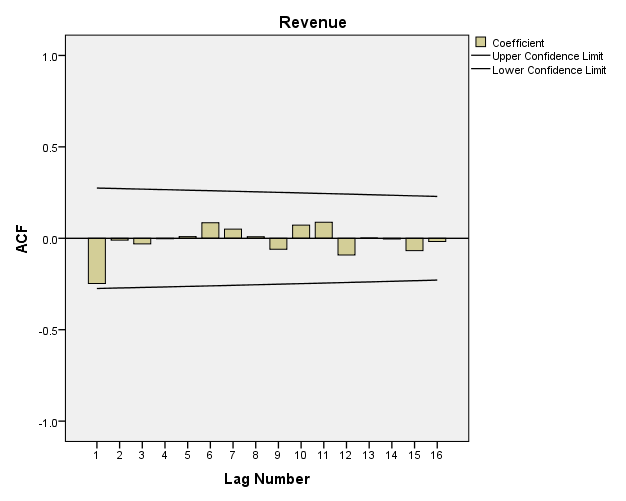
Biểu đồ ACF sau Differencing bậc 1 cho thấy các hệ số ACF giảm xuống giá trị 0 khá nhanh từ lag-1, tức các lag-k không có mối quan hệ với biến mục tiêu, dữ liệu Time series hoàn toàn ngẫu nhiên, không có tính thời vụ, hay xu hướng.
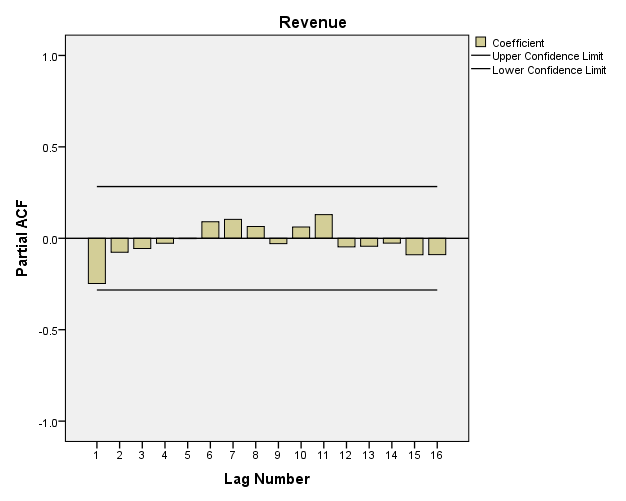
Cả 2 biểu đồ ACF, PCF, đều không có lag-k nào nằm ngoài vùng tin cậy, nên p và q cho AR và MA có thể bằng 0, với d = 1, thì chúng ta có dạng ARIMA (0, 1, 0).
Các bạn lưu ý theo quy tắc, dữ liệu áp dụng ARIMA phải là dữ liệu không có tính thời vụ, hay xu hướng, phải có tính dừng, là yếu tố đảm bảm đầu tiên. Và nó là điều kiện để áp dụng các mô hình tự hồi quy cho AR và MA. => Bước đầu tiên là phải kiểm tra tính dừng và tiến hành sai phân nếu có, sau đó mới xác định AR, MA.
Đây là dạng đặc biệt, gọi là Random Walk – ARIMA (0, 1, 0).
Công thức tổng quát
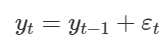
Nếu trung bình của các giá trị chênh lệch giữa các quan sát là khác 0, thì chúng ta có thêm phần c, là constant
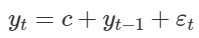
Kết quả SPSS cho ra c = -14.65 => Yt = -14.65 + Yt-1
Giả sử chúng ta thử tính ARIMA (1, 1, 1)


Yt = -24.473 + (-0.746)*Yt-1 + (-0.296)*εt-1
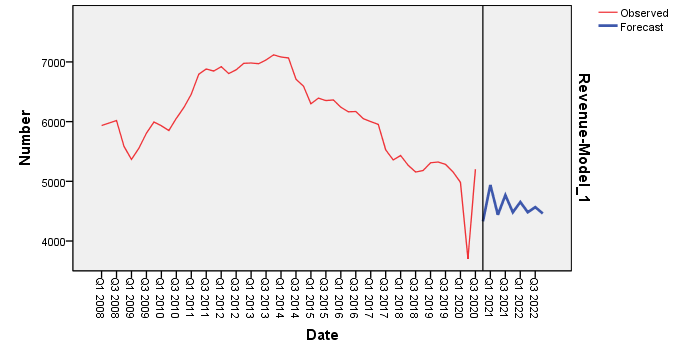
Mô hình trên để ví dụ cho các bạn mà thôi chứ hoàn toàn không thích hợp để dự báo khi các P-value > 0.05 ở các hệ số AR và MA, và kiểm định Ljung-box. Cần nhiều phương pháp khác trong xác định p, q, d để tìm ra mô hình phù hợp hơn với MSE, BIC nhỏ hơn mô hình trên, và các p-value của các hệ số < 0.05.
Ở các chuỗi bài viết khác sắp tới về Time series nếu có dịp chúng tôi sẽ giới thiệu các Rule, các lưu ý quan trọng trong mô hình ARIMA dựa trên kinh nghiệm của các chuyên gia đúc kết được. Đặc biệt là trong việc sử dụng PCF, ACF để xác định p, q cho AR và MA. Cách thức chúng tôi giới thiệu ở trên chỉ mang tính chất tham khảo, và chưa xét đến các quy tắc khác không được đề cập trong bài viết.
Mặc dù bài viết không lột tả hết được lý thuyết ARIMA một cách đầy đủ nhất, và cũng không hỗ trợ các bạn ứng dụng trong thực tế nhưng cũng là kiến thức cơ bản các bạn cần biết.
Hẹn gặp các bạn ở các bài viết sắp tới.
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.
“Statistics for Business and Economics” của tác giả Paul Newbold, William L. Carlson, Betty M. Thorne
“Data mining for Business analytics” của tác giả Galit Shmueli, Peter C. Bruce, Inbal Yahav, Nitin R. Patel, Kenneth C. Lichtendahl, Jr
https://otexts.com/fpp2/arima.html
https://people.duke.edu/~rnau/411arim.htm
https://phamdinhkhanh.github.io/2019/12/12/ARIMAmodel.html
http://machinelearningmastery.com/gentle-introduction-autocorrelation-partial-autocorrelation/
www.machinelearningplus.com/time-series/arima-model-time-series-forecasting-python/
ucanalytics.com/blogs/arima-models-manufacturing-case-study-example-part-3/


 English
English