Quay trở lại với chủ đề về kiểm định, phần kiểm định tham số (parametric test), ở bài viết phần 1 chúng ta đã tìm hiểu về phương pháp kiểm định tham số, tại sao gọi đây là phương pháp quan trọng nhất trong lĩnh vực thống kê, cũng như bàn luận về các vấn đề xung quanh giả thuyết thống kê, đặc biệt là hiểu cách vận hành của của phương pháp kiểm định.
Lưu ý bạn nào chưa tìm hiểu trước kiểm định tham số, chưa có kiến thức cơ bản về thống kê thì khó nắm bắt nội dung trong bài viết lần này. Bạn nào chưa tham khảo bài viết phần 1 có thể xem tại link dưới đây:
Tìm hiểu về phương pháp kiểm định tham số
Trong bài viết lần này của phần kiểm định tham số chúng ta sẽ đi qua các dạng kiểm định tham số dạng 1 mẫu độc lập với ví dụ cụ thể trong lĩnh vực kinh tế. Phương pháp kiểm định 2 mẫu chúng tôi sẽ nói ở bài viết sau.

Như vậy, nếu xét trên mẫu dữ liệu, phương pháp kiểm định tham số được chia làm 2 nhóm chính kiểm định trên một mẫu dữ liệu (kiểm định các kết luận về đặc trưng của tổng thể) và kiểm định trên nhiều hơn một mẫu dữ liệu (kiểm định 2 hay nhiều mẫu độc lập hoặc phụ thuộc để tìm sự khác biệt)
Nếu xét trên đặc trưng của tổng thể nghiên cứu, thì kiểm định tham số chia là 3 nhóm: kiểm định các giả thuyết liên quan đến trung bình của tổng thể, kiểm định các giả thuyết liên quan đến tỷ lệ tổng thể, kiểm định các giả thuyết liên quan đến phương sai của tổng thể.
Nếu cách đặt giả thuyết thì sẽ có 2 loại kiểm định chính là kiểm định 1 bên (1 phía) và kiểm định 2 bên (2 phía)
Nếu kiểm định 2 bên (Two – tail test)
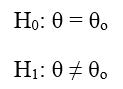
Nếu kiểm định 1 bên (One – tail test)
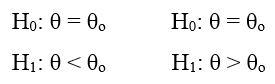
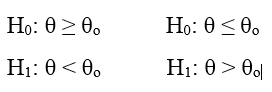
Bài viết này chúng ta sẽ đi vào dạng kiểm định một mẫu với ví dụ cụ thể, mong rằng sau bài viết này các bạn sẽ nắm rõ phương pháp kiểm định là gì, hiểu được kết quả kiểm định và có thể ứng dụng trong thực tế.
Kiểm định giả thuyết liên quan đến trung bình tổng thể (Population Mean)
Dạng kiểm định này áp dụng khi giả thuyết hay kết luận đưa ra có đề cập đến tham số trung bình của tổng thể mà chúng ta cần kiểm chứng.
Trường hợp mẫu lớn (n > 30)
Công thức:
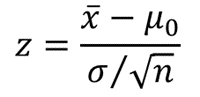
Quy tắc bác bỏ, tra bảng phân phối chuẩn để tìm Zα và Zα/2
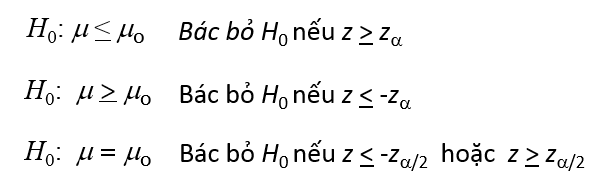
Quy tắc bác bỏ dựa trên p-value:
Nếu quy định trước một mức ý nghĩa α nào đó thì:
- p-value ≤ α thì bác bỏ giả thuyết H0, chấp nhận H1
- p-value > α thì chưa có cơ sở bác bỏ H0
Theo kinh nghiệm của một số chuyên gia thì chúng ta có thể xem xét bác bỏ p-value:
+ p-value > 0.1 thì không thể bác bỏ H0, thiếu cơ sở để kết luận H1 đúng
+ p-value nằm trong khoảng 0.05 – 0.1 thì không nên quả quyết bác bỏ H0, cơ sở để kết luận H1 đúng “còn yếu, chưa mạnh”.
+ p – value nằm trong khoảng 0.01 – 0.05 thì hướng về bác bỏ H0 , gần như có thể kết luận H1 đúng.
+ p-value < 0.01 thì chắc chắn bác bỏ H0, tự tin kết luận H1 đúng.
Nhìn theo đồ thị hàm mật độ xác suất theo phân phối chuẩn z đối với kiểm định 2 phía , chúng ta sẽ bác bỏ giả thuyết H0 (H1: θ = θo ) nếu:
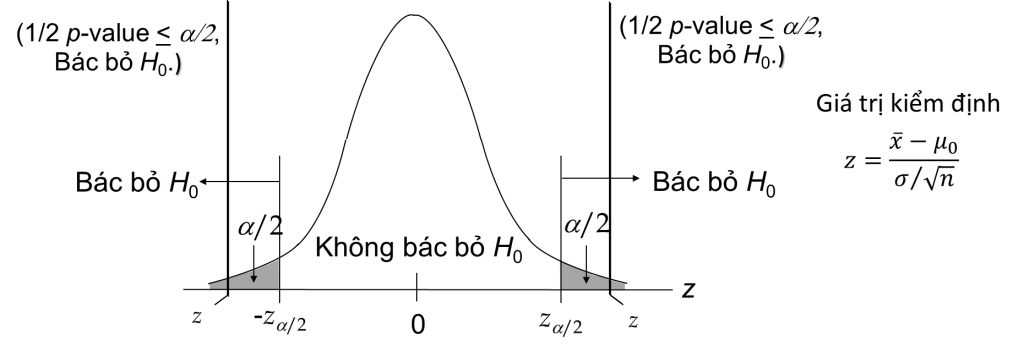
Kiểm định phía bên phải ((H1 : θ > θo), chúng ta sẽ bác bỏ giả thuyết H0 nếu:
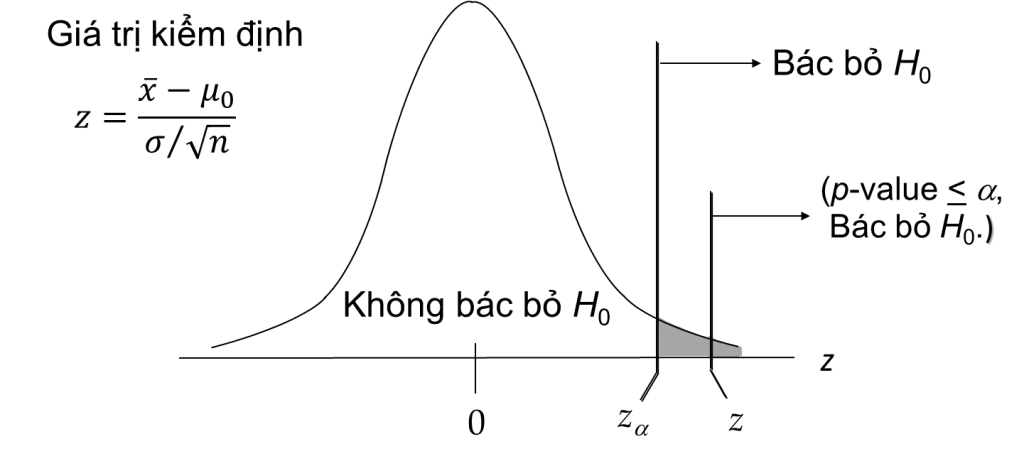
Kiểm định phía bên trái (H1 : θ < θo), chúng ta sẽ bác bỏ giả thuyết H0 nếu:

Vùng màu đen là miền bác bỏ, nếu z nằm trong vùng này chúng ta sẽ bác bỏ, và ngược lại. Tương tự phần diện tích thể hiện xác suất p-value nếu nằm trong phần diện tích được tô đen chúng ta sẽ bác bỏ giả thuyết.
Cách tra bảng phân phối chuẩn tắc của kiểm định z:
Nguyên tắc tra bảng cũng khá đơn giản, đối với kiểm định 1 phía chúng ta sẽ giữ nguyên giá trị α để tìm Zα.
Ví dụ α = 0.05 (mức ý nghĩa bằng 5%) chúng ta sẽ tìm giá trị xác suất tích lũy để có được Zα tức lấy 1 – 0.05 = 0.9500. Nhìn vào bảng dưới đây các bạn thấy không có giá trị 0.95 chỉ có 0.9495 và 0.9505, vậy chắc chắn 0.95 nằm trong khoảng 2 giá trị này. Chúng ta sẽ tìm Z của 0.9505 và 0.9495 rồi chia 2.
Cách xác định Zα chúng ta sẽ chiếu từ vị trí của giá trị xác suất tìm được sang cột ngoài cùng, và lên dòng trên cùng lấy 2 giá trị chiếu được cộng lại, ở đây là 1.6 + 0.04 = 1.64 và 1.6 + 0.05 = 1.65. Vậy Z0.5 = (1.64 + 1.65)/2 = 1.645
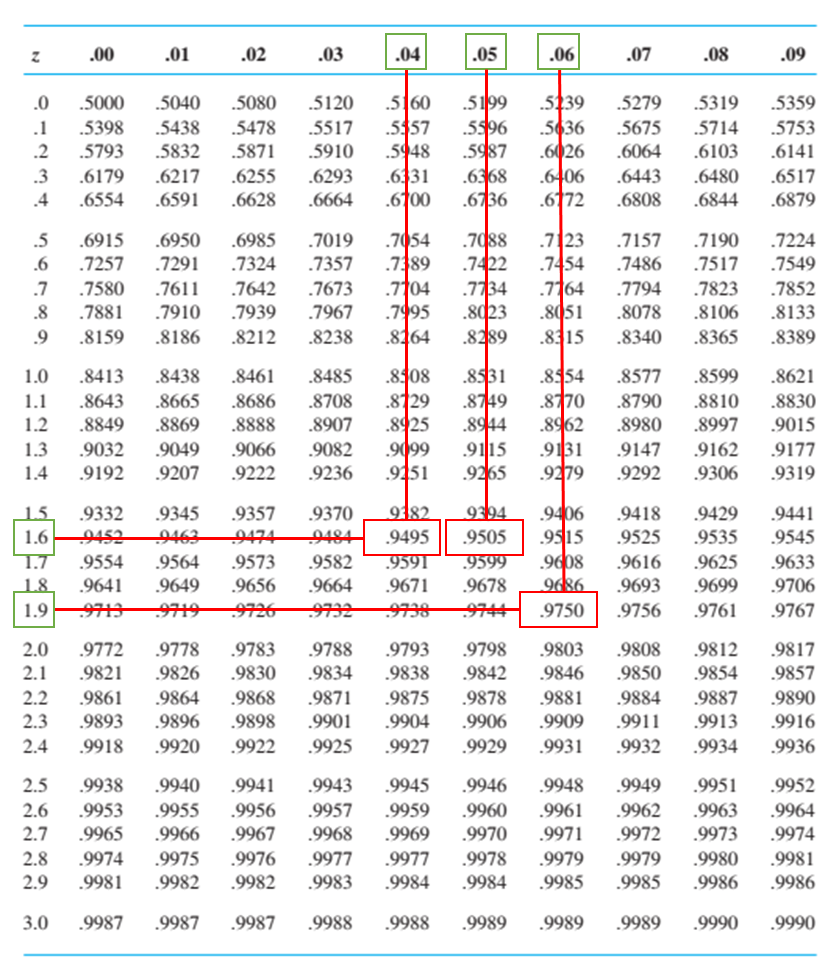
Kiểm định 2 phía thì chúng ta sẽ tim Zα/2 để so sánh với giá trị kiểm định, ví dụ α = 0.05, xác suất tích lũy để đạt Z0.025 là 1 – 0.025 = 0.975, làm tương tự ở trên chúng ta có được Z0.025 = 1.96.
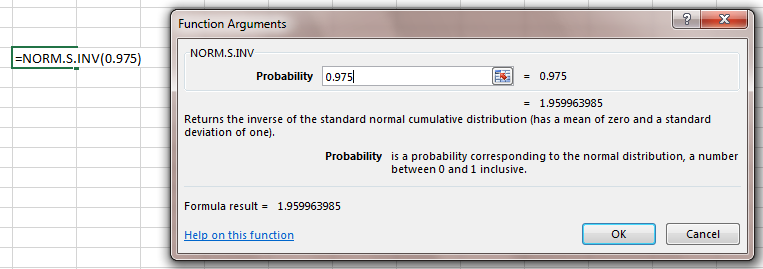
Trường hợp nếu các bạn không có bảng tra, các bạn có thể dùng phần mềm Excel để tìm:
Đánh vào ô trong sheet bất kỳ = NORM.S.INV (0.975) hoặc chọn FORMULAS => MORE FUNCTIONS => STATISTICAL => NORM.S.INV. Các bạn thấy kết quả xấp xỉ gần bằng kết quả bảng tra.
Như vậy chúng ta đã tìm hiểu xong công thức, chúng ta cùng đi vào ví dụ cụ thể:
Ví dụ:
Công ty sản xuất trang thiết bị văn phòng Jamestown Steel có các nhà máy sản xuất và dây chuyền sản xuất ở bang New York, Mỹ. Theo tiêu chuẩn, thì nhà máy tại Fredonia khi thành lập trung bình một tuần sẽ sản xuất được 200 thành phẩm là bàn văn phòng mẫu A235, độ lệch chuẩn là 16 thành phẩm. Trong năm vừa rồi, theo chiến lược mở rộng thị trường, các phương pháp sản xuất mới được áp dụng, và đội ngũ nhân viên tại nhà máy được gia tăng do tuyển dụng thêm người mới vào. Kết thúc năm, bộ phận điều hành công ty muốn biết rằng những thay đổi được áp dụng cho nhà máy có khiến số sản phẩm trung bình sản xuất 1 tuần có khác biệt so với con số 200 hay không, mức ý nghĩa α = 1%. Mức ý nghĩa thấp có thể do công ty chỉ muốn biết các biện pháp áp dụng cho nhà máy Fredonia có làm thay đổi năng lực sản xuất hay không, khác biệt nhỏ cũng có ý nghĩa.
Quản lý nhà máy lấy mẫu dữ liệu sản xuất (theo tuần) trong năm vừa qua của nhà máy, tổng cộng 50 tuần nhà máy làm việc. tính được giá trị trung bình về số lượng thành phẩm sản xuất là 203.5 thành phẩm.
Đặt giả thuyết kiểm định, ở đây công ty muốn biết có sự khác biệt sau khi áp dụng những thay đổi hay không nên:
H0: µ = 200
H1: µ≠ 200
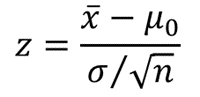
Với trung bình mẫu 203.5, độ lệch chuẩn 16, trung bình tổng thể theo giả thuyết là 200, số quan sát trong mẫu n = 50:
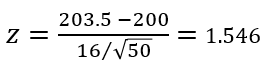
Mức ý nghĩa α = 0.01, mà đây là kiểm định 2 phía, nên chúng ta tìm Zα/2. Tra bảng phân phối chuẩn tắc, chúng ta có Zα/2 = 2.575
Theo quy tắc bác bỏ, vì Z < Zα/2 nên chúng ta không bác bỏ H0 tuy nhiên chưa có cơ sở kết luận giả thuyết H0 này đúng.
Cách xác định p-value:
Chúng ta tra bảng phân phối chuẩn tắc và tìm xem tại Z = 1.546 (=1.5 + 0.05 do 0.046 làm tròn), tức cột ngoài cùng tại vị trí 1.5, dòng trên cùng tại vị trí 0.05.
Xác suất tích lũy để đạt được Z = 1.546 theo bảng là 0.9394 các bạn có thể dùng hàm (=Norm.S.Dist (Z, True)), vì đây là kiểm định 2 phía nên:
P- value = 2*(1 – 0.9394) = 0.1212.
P-value > α = 0.01 nên chúng ta chắc chắn không thể bác bỏ H0. Để minh họa kết quả chúng ta cùng nhìn đồ thị dưới đây, giá trị kiểm định z không nằm trong miền bác bỏ, với phần diện tích của ½ p-value lớn hơn α/2
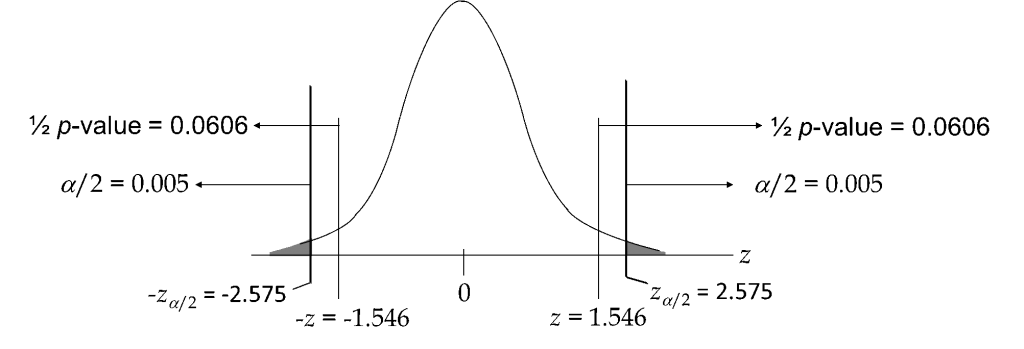
Như vậy sau khi áp dụng những thay đổi trong năm vừa qua, số lượng thành phẩm sản xuất một tuần trong nhà máy không có sự khác biệt với trước đây, tuy nhiên cần thu thập thêm dữ liệu để phân tích nhằm củng cố thêm cơ sở kết luận.
Lấy lại ví dụ trên nhưng giả sử thay vì bộ phận điều hành muốn tìm hiểu sự khác biệt thì họ muốn biết liệu các thay đổi có làm tăng năng lực sản xuất hay không, tức có làm tăng số lượng sản phẩm trung bình mỗi tuần cho nhà máy Fredonia hay không. Cách đặt giả thuyết sẽ khác:
H0: µ ≤ 200
H1: µ > 200
Đây là kiểm định 1 bên, chúng ta vẫn giữ nguyên công thức tính giá trị kiểm định, chỉ khác ở cách tra bảng chuẩn tắc, và quy tắc loại bỏ
Z = 1.546
Chúng ta tìm Zα thay vì Zα/2, theo bảng phân phối chuẩn tắc, với mức ý nghĩa 0.01, Zα = 2.33.
Tiếp tục theo nguyên tắc bác bỏ, Z < Zα nên chúng ta cũng không thể bác bỏ H0, tức số lượng sản phẩm không tăng hơn 200, năng lực sản xuất không tăng sau khi áp dụng các thay đổi.
P-value = 1 – 0.9394 = 0.0606 (lưu ý không nhân 2)
P- value > α = 0.01 nên không bác bỏ H0 là hợp lý.
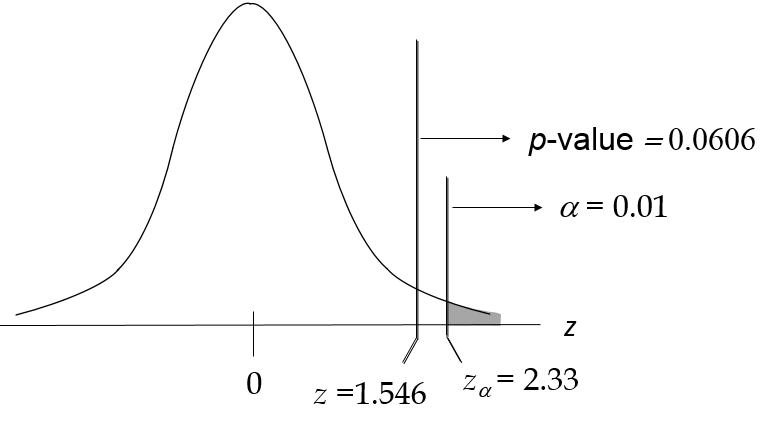
Z không nằm trong miền bác bỏ (vùng màu đen), phần diện tích p-value lớn hơn α
Lưu ý quan trọng
Trường hợp kiểm định z như trên với phân phối chuẩn tắc, áp dụng khi mẫu dữ liệu lớn, cụ thể theo kinh nghiệm của các chuyên gia, và theo các giáo trình thống kê quốc tế, là trên 30 quan sát, tức n > 30. Con số 30 suy ra được từ định lý giới hạn trung tâm (Central Limit Theorem).
Ngoài ra, trường hợp không biết độ lệch chuẩn của tổng thể σ chúng ta sẽ tính toán độ lệch chuẩn của mẫu hiệu chỉnh ký hiệu s để thay thế vào công thức.
Trong thực tế, để củng cố kết quả phân tích người ta sẽ cố gắng thu thập dữ liệu mẫu nhiều hơn, nên thông thường kiểm định z sẽ phổ biến hơn kiểm định t mà chúng tôi sắp nói dưới đây.
Hướng tiếp cận khác trong kiểm định
Bổ sung thêm cho các bạn. Thay vì tính toán giá trị kiểm định, chúng ta có thể sử dụng phương pháp ước lượng khoảng tin cậy (Confidence Interval). Các bạn có thể xem lại tại bài viết dưới đây:
Tổng quan về Statistics: Inferential statistics (thống kê suy luận)
Cụ thể nếu giá trị trung bình của tổng thể được nêu ra trong giả thuyết H0 mà nằm trong khoảng tin cậy được ước lượng thì giả thuyết H0 sẽ không bị bác bỏ. Hướng tiếp cận thường được áp dụng chủ yếu cho kiểm định 2 bên.
Công thức ước lượng khoảng:

Lấy lại ví dụ ở trên:
Khoảng tin cậy tìm được là 203.5 ± 2.575*(16/căn (50)) = 203.5 ± 5.826 = (197.6; 209.3)
Như vậy µ0 = 200 có thể nằm trong khoảng tin cậy, chúng ta sẽ không bác bỏ H0.
Trường hợp mẫu nhỏ (n ≤ 30)
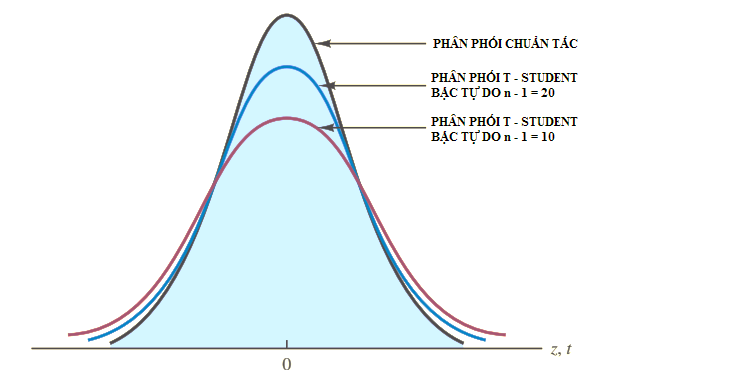
Đối với trường hợp mẫu nhỏ và độ lệch chuẩn chưa biết, chúng ta sẽ sử dụng kiểm định t thay vì kiểm định z, và quy luật phân phối áp dụng sẽ là t-student hay phân phối t. Phân phối t là dạng phân phối giả định từ phân phối chuẩn (Normal distribution), khi mẫu dữ liệu càng lớn, bậc tự do n – 1 càng cao, thì phân phối t sẽ dần tiến đến phân phối chuẩn.
Minh họa cho phân phối t Student:
Công thức kiểm định t

Bậc tự do (Degrees of freedom) = n – 1.
Giải thích bậc tự do khá phức tạp các bạn có thể tham khảo ở các tài liệu khác. Ở đây chúng tôi gợi ý cho các bài bài viết của Minitab giải thích bậc tự do, các bạn có thể xem qua.
Ví dụ các bạn có 7 bộ quần áo mặc để đi làm và mục đích là mỗi ngày phải mặc khác nhau, vậy ngày thứ nhất bạn mặt bộ quần áo A, ngày thứ hai bạn được chọn tùy ý trong 6 bộ còn lại, ngày thứ ba là 5 bộ còn lại,… đến ngày thứ 6 bạn chỉ còn 2 bộ để tùy ý chọn, nhưng đến ngày thứ 7 bạn còn duy nhất 1 bộ, bạn không được phép chọn lựa. Như vậy trong 7 ngày, có 6 ngày bạn được phép chọn tùy ý. Đây là một cách hiểu đơn giản về degree of freedom.
Về quy tắc bác bỏ trong kiểm định t cùng tương tự như kiểm định z:
Quy tắc bác bỏ, tra bảng t Student bậc tự do n – 1
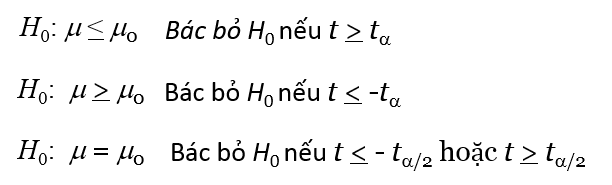
Quy tắc bác bỏ dựa trên p-value cũng tương tự kiểm định Z và cách thể hiện trên đồ thị hàm số cũng tương tự kiểm định Z. Tuy nhiên cách tính p-value cũng có chút khác biệt, cách tra bảng phân phối t để tìm tn – 1, α/2 cũng vậy.
Ví dụ
Công ty Samsung trước khi cho ra mắt sản phẩm mới, đã khảo sát hơn 2000 người trưởng thành sống tại Vương quốc Anh, mục đích để tìm hiểu hành vi người dùng, xem cách người trưởng thành sử dụng smartphone, hay smartphone thường được dùng để làm gì. Chuyên gia thực hiện khảo sát kết luận thời gian trung bình sử dụng điện thoại 1 ngày của người trưởng thành là trên 120 phút. Để đảm bảo kết luận là đúng, một chuyên gia khác đã hỏi trực tiếp 10 khách hàng tại Anh, những người này đã có việc làm, và vừa rồi có cơ hội thử nghiệm sản phẩm mới của Samsung. Thông tin thời gian sử dụng smartphone trung bình 1 ngày thu thập từ 10 khách hàng như sau:
100; 90; 75; 130; 150; 180; 160; 110; 90; 140
Chúng ta sẽ đặt giả thuyết H1: µ > 120 do muốn mục đích kiểm định là kiểm tra thực tế có phải trung bình sử dụng smartphone của 1 người trưởng thành trên 120 phút có đúng không.
H0: µ ≤ 120
H1: µ > 120
Do không biết độ lệch chuẩn σ của tổng thể, chúng ta phải ước lượng bằng cách tính độ lệch chuẩn mẫu hiệu chỉnh của tập dữ liệu 10 quan sát ở trên. Công thức tính:
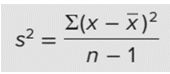
s tính được = 34.74, trung bình mẫu = 122.5
Giá trị kiểm định tính được:
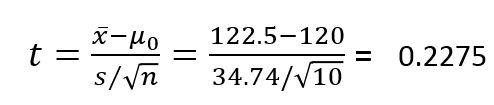
Giả sử mức ý nghĩa α = 5%, vì đây là kiểm định 1 bên nên cách tra bảng t như sau:
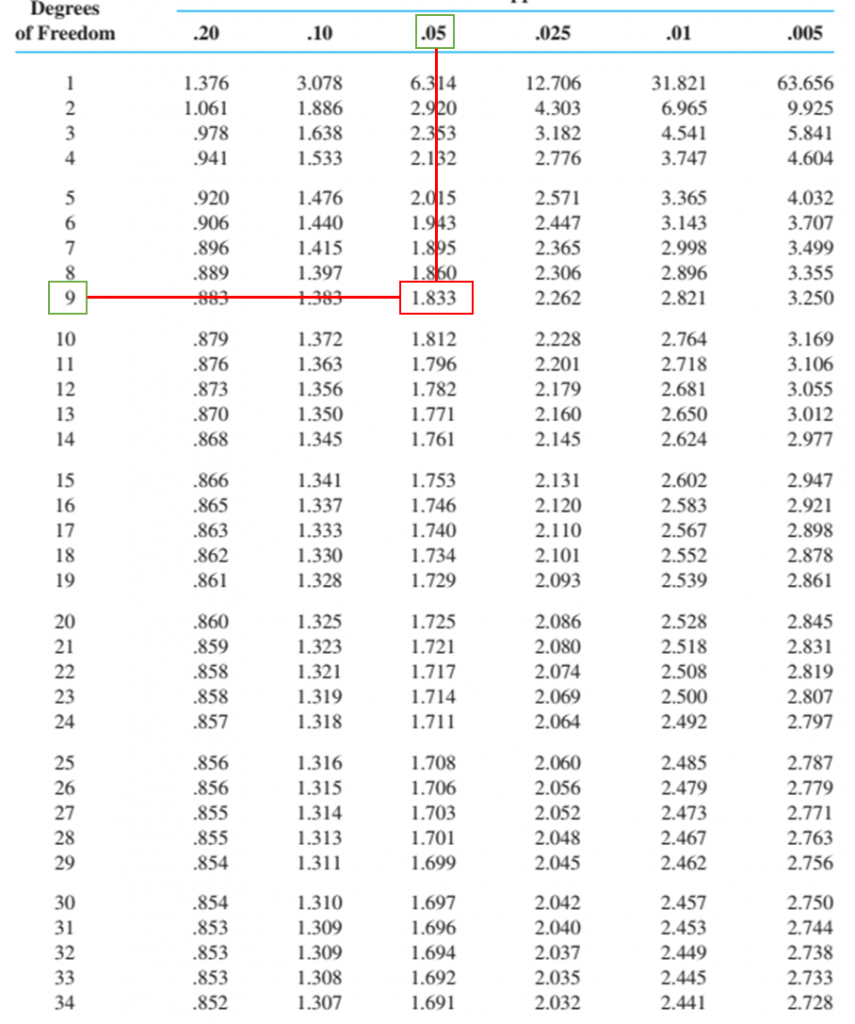
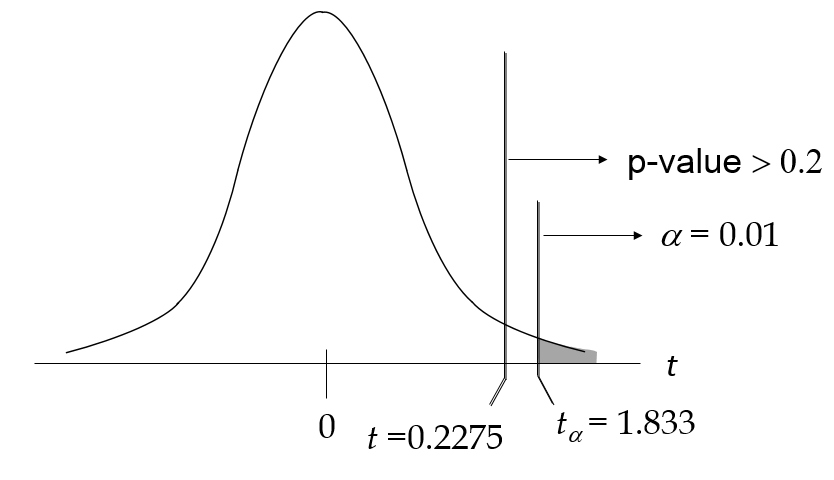
Bậc tự do = n – 1 = 10 – 1, α = 0.05 => t9, 0.05 = 1.833
Vì t < t 9, 0.05 nên chúng ta không bác bỏ giả thuyết H0 tức không thể kết luận chính xác thời gian trung bình 1 người trưởng thành tại Anh sử dụng Smartphone là trên 120 phút, cần thu thập thêm dữ liệu để phân tích và chứng minh thêm.
Chúng ta cùng tìm p-value. Cách tìm p-value khác so với kiểm định Z là do bảng phân phối chuẩn tắc cung cấp dữ liệu về giá trị xác suất tích lũy ứng với giá trị Z (lấy đến số thập phân thứ 2) cụ thể và chính xác còn bảng phân phối t thì ngược lại, các giá trị trong bảng là giá trị t, còn dòng trên cùng mới là xác suất (dòng chỗ Degree of freedom) mà xác suất ở đây là p-value không phải xác suất tích lũy để đạt được t nên không cần lấy 1 – p tra bảng như kiểm định Z. Chỉ có ước lượng mà thôi. Các bạn xem qua 2 đồ thị dưới đây sẽ rõ:
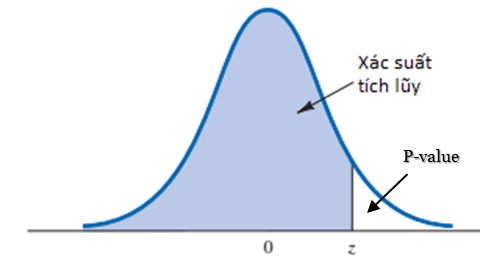
Bảng tra phân phối chuẩn tắc phổ biến thường xác định xác suất tích lũy (phần màu xanh) là xác suất tích lũy để đạt được z => p-value = 1 – p (Z).
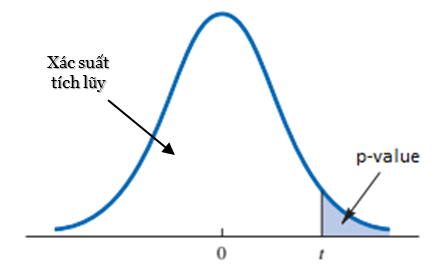
Bảng phân phối t phổ biến thường thể hiện giá t, dòng trên cùng thể hiện giá trị xác suất p-value (phần màu xanh), hay nói cách khác là 1 – p tích lũy, hay phần diện tích, phần xác suất nằm ở đuôi trên (upper – tail theo một số tài liệu thống kê) và phần màu xanh này có thể chứa hay không chứa phần diện tích của α. Nếu chứa α, p-value > α và ngược lại
Nhìn lại bảng t trên, ở dòng bậc tự do = 9, các bạn thấy t = 0.883 là nhỏ nhất mà ở đó xác suất = 0.2, vậy t = 0.2275 chắc chắn p-value > 0.2 (chiều xác suất tăng theo trên bảng là từ phải về trái, xem dòng trên cùng). Đồng nghĩa p-value chắc chắn sẽ > α do đó không thể bác bỏ giả thuyết H0. Trường hợp kiểm định 2 phía thì chúng ta cứ việc nhân 2 p-value như kiểm định Z.
Để các bạn hiểu hơn cách ước lượng p-value, giả sử t = 2.5, tại dòng bậc tự do 9, t = 2.5 sẽ nằm giữa 2.262 và 2.821, tức p-value sẽ nằm giữa 0.01 và 0.025, với α = 0.05, chắc chắn p-value sẽ nhỏ hơn, và bác bỏ giả thuyết H0. Nếu kiểm định 2 bên, thì p – value sẽ nằm giữa 2*0.01 và 2*0.025.
Việc tìm chính xác p-value có thể thực hiện qua các phần mềm thống kê, phần mềm phân tích và cả phần mềm excel. Các bạn có thể dùng hàm T.Dist.RT(t, bậc tự do) hoặc 1 – T.Dist(t, bậc tự do, True)
Kiểm định 2 bên, hay kiểm định bên trái, phương pháp triển khai cũng tương tự, các bạn lưu ý cách xác định p-value và quy tắc bác bỏ H0 để tránh nhầm lẫn.
Lưu ý quan trọng:
Kiểm định t luôn được áp dụng khi trường hợp chúng ta không biết gì về độ lệch chuẩn σ của tổng thể, phải sử dụng độ lệch chuẩn của mẫu đã hiệu chỉnh là s, do đó trong một số tài liệu thống kê, không bắt buộc n > 30 phải kiểm định Z, vẫn có thể sử dụng kiểm định t khi không biết về σ. Kiểm định t áp dụng khi quy luật phân phối của tổng thể có thể xấp xỉ chuẩn.
Tuy nhiên trong thực tế, kiểm định t cho thấy sự thiếu chính xác so với kiểm định Z khi cả 2 tham số đặc trưng quan trọng của tổng thể trung bình µ và độ lệch chuẩn σ đều là ước lượng, còn kiểm định Z thì biết trước σ. Nên kiểm định Z thường được ưu tiên khuyến khích việc thu thập dữ liệu nhiều hơn.
Thế nhưng, không phải lúc nào cũng biết trước được độ lệch chuẩn σ của tổng thể, và khi mẫu dữ liệu quá lớn (ví dụ trên n > 100), thì kiểm định t có thể sẽ không hiệu quả (giá trị kiểm định t có xu hướng tăng, còn giá trị t tra bảng có thể nhỏ dần, dần đến khả năng cao, H0 không bị bác bỏ, nếu H0 sai thực sử, thì tỷ lệ mắc sai lầm loại II là lớn). Mặt khác khi mẫu dữ liệu càng lớn, thì s có giá trị ước lượng sẽ chính xác hơn, gần bằng σ
Do đó, như đề cập ở phần lưu ý, trong một số trường hợp khả dĩ, kiểm định Z chúng ta có thể sử dụng s thay cho σ mà không cần kiểm định t.
Lưu ý sau cùng, kiểm định Z chắc chắn được áp dụng với độ lệch chuẩn σ của tổng thể đã biết bất kể mẫu dữ liệu như thế nào.
Kiểm định giả thuyết về tỷ lệ tổng thể (Population Proportion)
Điều kiện áp dụng: n.p ≥ 5 và n.(1 – p) ≥ 5

Với

Quy tắc bác bỏ, Zα và Zα/2 tra bảng
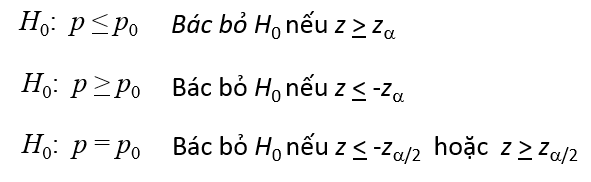
Ví dụ về tỷ lệ tổng thể cho các bạn hiểu rõ thêm nó là gì. Tỷ lệ khách hàng mua sắm tại các siêu thị tại thành phố Hố Chí Minh là nữ chiếm 70%. Tỷ lệ học sinh học trường chuyên trúng tuyển vào Đại học Ngoại Thương là 60%. Tỷ lệ khách hàng để lại liên hệ sau lần đầu ghé thăm website bán hàng là 30%,… Như vậy để kiểm tra các giả thuyết hay kết luận trên chúng ta cần thu thập tập dữ liệu mẫu, tìm tỷ lệ trong tập dữ liệu mẫu để tính giá trị kiểm định.
Công thức kiểm định cũng giống với kiểm định giả thuyết về trung bình tổng thể, giả định về quy luật phân phối chuẩn cũng tương tự, Tuy nhiên khác biệt chính là có sự ràng buộc về kích thước mẫu và tỷ lệ tổng thể đưa ra trong giả thuyết, như đề cập ở dòng đầu tiên thì mới có thể xấp xỉ phân phối của tỷ lệ mẫu (Sampling distribution of proportion) theo phân phối chuẩn, tức P^ ~ N (p, p*q/n) với q = 1 – p, độ lệch tiêu chuẩn của phân phối mẫu giống như công thức ở trên, tỷ lệ mẫu trung bình µp^ = p
Công thức kiểm định ở trên tức là công thức chuẩn hóa của tỷ lệ mẫu sang giá trị Z của phân phối chuẩn tắc trên cơ sở quy luật phân phối của tỷ lệ mẫu đã xấp xỉ chuẩn.
Do đó chỉ khác công thức nhưng việc bác bỏ và kết luận dựa trên giá trị z, giá trị z tra bảng và p-value là giống với trường hợp kiểm định trung bình mẫu. Nên chúng tôi không nhắc lại ở đây.
Lưu ý, đối với tỷ lệ mẫu chúng ta thường chỉ có áp dụng kiểm định Z mà thôi do theo điều kiện ở trên mẫu thường lớn, và chúng ta biết được độ lệch tiêu chuẩn của tỷ lệ mẫu tìm được mà không cần xác định độ lệch chuẩn σ của tỷ lệ trong tổng thể. Còn ở kiểm định trung bình mẫu, thì độ lệch tiêu chuẩn của trung bình mẫu σx = σ/ căn bậc 2 (n), chúng ta phải xác định σ của tổng thể, nếu không phải xấp xỉ, dùng s thay thế.
Ví dụ:
Một công ty bán lẻ thử nghiệm kênh bán hàng online trên website đã được 8 tháng, dự định sẽ triển khai các hoạt động thương mại điện tử trên quy mô lớn song song với sử dụng các cửa hàng truyền thống. Một cuộc khảo sát khách hàng về mức độ hài lòng khi trải nghiệm những dịch vụ trên kênh bán hàng online, và sự ưu tiên của họ giữa kênh bán hàng online và truyền thống đã được thực hiện trong tháng vừa qua. Bộ phận điều hành công ty thông báo trước đó nếu tỷ lệ khách hàng thích kênh bán hàng online trên 70%, công ty sẽ chuyển đổi cơ cấu, thay đổi các quy trình, tinh chỉnh các chức năng cốt lõi, tập trung đầu tư để hướng sang thương mại điện tử.
Lấy mẫu ngẫu nhiên 100 khách hàng từ hơn 10000 khách hàng được khảo sát tại khắp các hệ thống cửa hàng truyền thống, và những ai đã trải nghiệm kênh bán hàng online để lại feedback. Trong 100 khách hàng, có 85 người thích kênh bán hàng online và đánh giá tốt kênh bán hàng online đang được thử nghiệm. Bộ phận khảo sát sẽ tiến hành kiểm định với mức ý nghĩa 5%.
Vì mục đích nghiên cứu xem tỷ lệ thích kênh bán hàng online có trên 70% hay không nên chúng ta đặt H1: p > 70%, H0: p ≤ 70%
Tinh tỷ lệ p theo mẫu được p = 85/100 = 0.85, q = 1 – 0.85 = 0.15
Xét điều kiện n.p ≥ 5 và n.(1 – p) ≥ 5. Thì 100*0.85 = 85 ≥ 5 và 100*(1-0.85) = 15 ≥ 5, nên chúng ta yên tân áp dụng được công thức kiểm định Z.
Chúng ta thay vào công thức như sau:
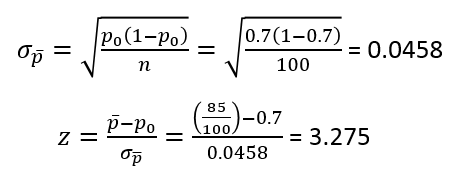
Tra bảng Zα = Z0.05 = 1.645 (kiểm định 1 bên)
Chúng ta thấy Z > Z0.05 nên có thể bác bỏ H0, tức tỷ lệ khách hàng ưu tiên kênh bán hàng online cao hơn 70%. Như vậy công ty sắp tới có thể triển khai các hoạt động thương mại điện tử.
p-value tìm được = 1 – 0.999472 = 0.000528 chắc chắn < mức ý nghĩa 5% nên yên tâm bác bỏ H0.
Như vậy đến đây là kết thúc phần 1 bài viết các dạng kiểm định tham số trên một mẫu. Ngoài ra còn một dạng khác là kiểm định giả thuyết về phương sai của tổng thể thì các bạn có thể tham khảo thêm ở các tài liệu khác do trong thực tế dạng này ít được sử dụng phổ biến, và quy trình thực hiện thường phức tạp hơn.
Ở bài viết tới chúng ta sẽ sang các phương pháp kiểm định tham số trên 2 mẫu với 2 mẫu độc lập và 2 mẫu là 2 mẫu cặp.
Tài liệu tham khảo
“Statistics” của các tác giả James T. McClave, Terr y Sincich
“Essentials of Statistics for The Behavioral Sciences” của các tác giả Frederick J Gravetter, Larry B. Wallnau, Lori-Ann B. Forzano
“Basic statistics for business and economics” của các tác giả Douglas A. Lind, William G. Marchal, Samuel A. Wathen
“Statistics for Business and Economics” của các tác giả David R. Anderson, Dennis J. Sweeney, Thomas A. Williams và cộng sự
www.analyticsvidhya.com/blog/2015/09/hypothesis-testing-explained/
https://www.statisticshowto.com/probability-and-statistics/hypothesis-testing
hub.packtpub.com/how-data-scientists-test-hypotheses-and-probability/
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English