Ở bài viết trước BigDataUni và các bạn đã cùng tìm hiểu kỹ về nguồn gốc phương trình hồi quy logistic, với đi qua ví dụ khác để giải thích phương trình, giải thích các hệ số hồi quy, đồng thời dùng phương trình để ước lượng xác suất thể hiện khả năng Y = 1, qua đó đánh giá sự tác động của một biến độc lập hay một yếu tố lên biến mục tiêu Y. Đó là cách diễn giải phương trình hồi quy logistic dựa vào hệ số hồi quy, và kết quả ước lượng. Ở bài viết lần này chúng ta cùng tìm hiểu qua odds, odds ratio, cách odds ratio phân tích sâu hơn về mối quan hệ giữa các biến độc lập lên biến mục tiêu. Ở bài viết sắp tới phần 4, chúng ta sẽ đi qua phần quan trọng khác trong hồi quy logistic chính là Maximum likelihood estimation method với các phương pháp đánh giá độ phù hợp của phương trình hồi quy logistic, cũng như phương pháp đánh giá độ chính xác của mô hình trong việc dự báo giá trị biến mục tiêu y.
Các bạn có thể tham khảo những bài viết trước của chúng tôi tại các link dưới đây:
Tổng quan về Logistic regression (hồi quy Logistic) (Phần 1)
Tổng quan về Logistic regression (hồi quy Logistic) (Phần 2)
Phương trình hồi quy logistic đơn biến:
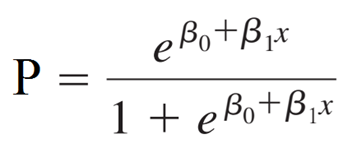
Phương trình tổng quát của hồi quy logistic
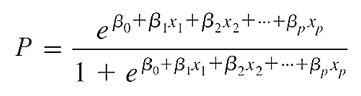
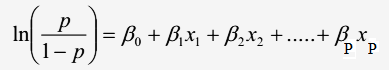
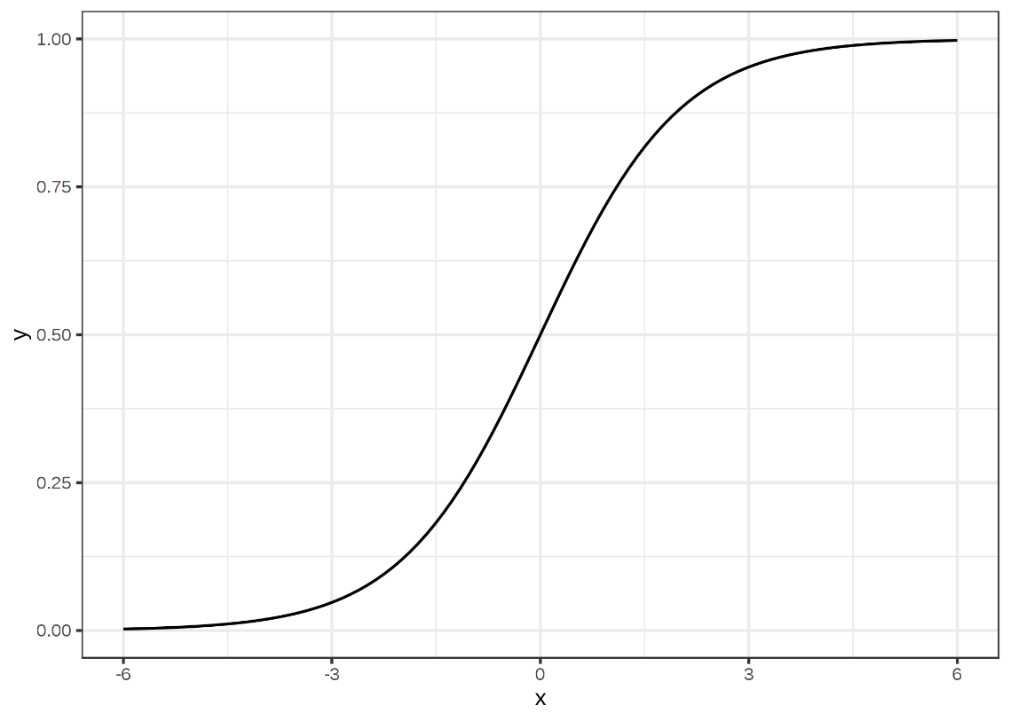
Đồ thị mô tả
Diễn giải phương trình hồi quy logistic dựa vào Odds ratio
Lưu ý quan trọng trước khi đi vào phần này đó chính là chúng ta phân tích odds để tìm hiểu, nghiên cứu sâu hơn về mối quan hệ giữa các biến độc lập và biến mục tiêu, chứ odds không phải là kết quả quan tâm sau cùng của mô hình phân tích hồi quy logistic mà là kết quả dự báo hay kết quả phân loại của biến mục tiêu.
- Phân tích mối liên hệ giữa biến độc lập với biến mục tiêu dựa vào odds
Khi giải thích một phương trình hồi quy chúng ta phải liên hệ những biến độc lập thông qua hệ số hồi quy được ước lượng từ phương trình với những câu hỏi, vấn đề đặt ra trong thực tế mà cụ thể là biến mục tiêu. Tuy nhiên với hồi quy logistic, chúng ta khó có thể liên hệ giữa các biến độc lập và xác suất thể hiện khả năng y = 1 nếu chỉ dựa vào kết quả ước lượng xác suất từ phương trình tìm được là chưa đủ. Ví dụ biến A, biến B tác động như thế nào đến kết quả tính toán được từ phương trình, lớn hay nhỏ?
Chúng ta không biết cụ thể, hơn nữa logistic regression là một dạng hồi quy phi tuyến, đồ thị không phải là đường thẳng mả là đường cong chữ S và các hệ số hồi quy không thể thể hiện sự biến động của xác suất p khi các biến x thay đổi 1 đơn vị, nên không thể xét hệ số hồi quy càng cao thì mối liên hệ giữa biến độc lập và biến mục tiêu càng mạnh. Chúng ta không thể biết chính xác.
Tuy nhiên các chuyên gia phân tích cũng như các nhà thống kê chỉ ra rằng thông qua Odds và Odds ratio một cách gián tiếp chúng ta có thể phân tích mối liên hệ.
Odds thể hiện khả năng một sự kiện có thể xảy ra bằng cách lấy tỷ lệ xác suất xảy ra chia cho xác suất không xảy ra. Odds không phải là thuật ngữ xuất hiện đầu tiên trong lĩnh vực phân tích dữ liệu, mà thực chất nó phổ biến rất nhiều trong các trò chơi cá cược, đánh bạc. Nếu xác suất bạn đặt cược toàn bộ số tiến của mình và thắng ván bài là 0.2, thì tỷ lệ thất bại là 1 – 0.4 = 0.6. Odds lúc này sẽ bằng 0.4/0.6 = 2/3, tức trung bình bạn có thể sẽ thắng 2 ván sau mỗi 3 ván thua. Công thức tính odds nhắc lại từ bài viết trước
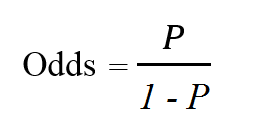
Odds ratio là tỷ lệ của 2 odds đo lường tác động của một biến độc lập lên odds khi giá trị của biến này thay đổi 1 đơn vị, và các biến còn lại được giữ nguyên. Dễ hiểu hơn, chúng ta có odds (odds(1)) của y = 1 (là xác suất p khi y = 1 chia cho 1 – p) khi một biến độc lập thay đổi 1 đơn vị chia cho odds (odds(0)) của y = 1 (là xác suất p khi y = 1 chia cho 1 – p) khi giá trị của các biến độc lập giữ nguyên không thay đổi. Lưu ý thông thường odds hướng đến y = 1 không phải y = 0, nên p được xem là xác suất xảy ra y = 1.
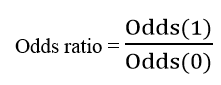
Theo Wikipedia, Odds ratio là một chỉ số thống kê đánh giá độ mối liên kết giữa hai sự kiện A và B. Odds ratio là tỷ lệ của khả năng xảy ra sự kiện A (giống Odds(1)) khi sự kiện B đã xảy ra và khả năng xảy ra của sự kiện A khi không có sự kiện B (giống Odds(0)), hoặc ngược lại, tỷ lệ của khả năng xảy ra sự kiện B khi sự kiện A xảy ra và khả năng xảy ra sự kiện B khi không có sự kiện A. Hai sự kiện là độc lập khi và chỉ khi Odds ratio bằng 1, tức là khả năng xảy ra của các sự kiện là như nhau. Nếu Odds ratio lớn hơn 1, thì A và B tương quan thuận với nhau sự hiện diện của B làm tăng khả năng xảy ra sự kiện A và hoặc ngược lại, nếu Odds ratio nhỏ hơn 1, thì A và B có mối tương quan ngược chiều và sự hiện diện của một sự kiện sẽ làm giảm khả năng xảy ra của sự kiện khác. Giải thích như vậy có thể các bạn sẽ khó hiểu, hãy cùng BigDataUni đi vào ví dụ dưới đây.
Chúng ta cùng quay lại với ví dụ bài viết trước để xem có thể đánh giá mối liên hệ giữa các biến độc lập x với xác suất ước lượng để kết luận y = 1 hay không.
Nhắc lại ví dụ: một công ty bán lẻ các sản phẩm công nghệ, điện tử có các cửa hàng nằm trong 2 tỉnh thành khác nhau, công ty tháng trước đã triển khai một chương trình ưu đãi dành cho khách hàng thân thiết. Công ty đã thiết kế một email quảng cáo để gửi đến những khách hàng của mình ở tỉnh A, bao gồm những khách hàng có thẻ thành viên và những khách hàng không có thẻ thành viên. Công ty muốn phân tích xem số tiền mà mỗi khách hàng bỏ ra trong 1 năm qua và đăng ký thẻ thành viên có tác động như thế nào đến việc khách hàng tham gia chương trình ưu đãi. Chương trình ưu đãi cụ thể là nhận phiếu giảm giá 25%, khi tổng giá trị hàng mua là trên 5 triệu. Lấy mẫu 100 khách hàng thì có 40 khách hàng tham gia bằng cách click vào link đăng ký trong email, 60 khách hàng còn lại thì không. Công ty muốn dự báo hay phân loại một nhóm khách hàng ở của tỉnh B có khả năng đăng ký chương trình ưu đãi hay không nếu dựa vào kết quả phân tích để quyết định tháng tới có làm chương trình tương tự hay không.
Biến mục tiêu là khả năng đăng ký chương trình ưu đãi với y = 1 – sẽ đăng ký chương trình, y = 0 – không đăng ký chương trình. Biến độc lập x1 là số tiền khách hàng bỏ ra trong năm vừa rồi (đơn vị triệu VND). Biến độc lập x2 là thông tin về đăng ký thẻ thành viên, x2 = 1 là có thể thành viên, x2 = 0 là không có thể thành viên.
Các bạn có thể tải data theo link google drive tại đây.
Cụ thể sau khi sử dụng phần mềm để tìm phương trình hồi quy logistic, chúng ta được kết quả như sau:
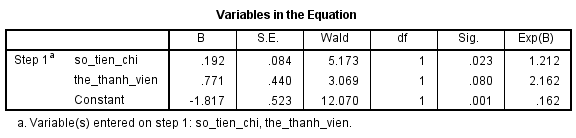
Chú ý vào cột hệ số hồi quy và chúng ta có phương trình như sau:
E(y) = P = (e(-1.817 + 0.192*x1 + 0.771*x2))/ (1 + e(-1.817 + 0.192*x1 + 0.771*x2))
Chúng ta sẽ tính toán lần lượt giá trị odds(1) và odds(0) cho ví dụ này. Bây giờ chúng ta sẽ áp dụng cho công thức tính odds, với odds(1) là trường hợp có thẻ thành viên, odds(0) là trường hợp không có thẻ thành viên. Như vậy, biến chúng ta sẽ dùng để tính odds ratio là biến đăng ký thẻ thành viên, là biến thay đổi với giá trị thay đổi từ 0 đến 1, còn biến giữ nguyên sẽ là biến số tiền chi năm rồi, các bạn xem lại ở phía trên đầu phần này nếu không hiểu.
Xét với số tiền khách hàng bỏ ra năm ngoái là 3 triệu, chúng ta lấy x1 = 3 cho cả 2 odds (1), odds (0). Theo công thức tổng quát về ước lượng giá trị odds theo xác suất được ước lượng ta có:
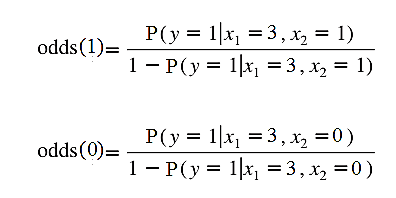
Lấy lại kết quả ước lượng xác suất ở bài viết trước:
Trường hợp khách hàng có thẻ thành viên, số tiền chi ra trong năm ngoái là 3 triệu.
E(y1) = P của odds(1) = (e(-1.817 + 0.192*3 + 0.771*1))/ (1 + e(-1.817 + 0.192*3 + 0.771*1)) = 0.385
Trường hợp khách hàng không có thẻ thành viên, số tiền chi ra trong năm ngoái là 3 triệu.
E(y1) = P của odds(0) = (e(-1.817 + 0.192*3 + 0.771*0))/ (1 + e(-1.817 + 0.192*3 + 0.771*0)) = 0.224
Odds(1) = P/ (1 – P) = (0.385)/ (1 – 0.385) = 0.625
Odds(0) = P/ (1 – P) = (0.224)/ (1 – 0.224) = 0.288
Lưu ý những kết quả ở trên, tất cả đều là giá trị ước lượng chứ không hoàn toàn chính xác trong thực tế. Đây cũng là lưu ý khi chúng ta tính toán kết quả từ phương trình hồi quy ở những dạng hồi quy khác.
Tỷ lệ odds ước lượng được:
Odds ratio = 0.626/ 0.288 = 2.16
Như vậy thông qua odds ratio, chúng ta có thể nhận xét với cùng số tiền chi ra cho mua hàng năm ngoái (đơn vị triệu đồng) khách hàng có thẻ thành viên có tỷ lệ odds thể hiện khả năng khách hàng đăng ký ưu đãi cao hơn 2 lần so với khách hàng không có thẻ thành viên.
Odds ratio thể hiện rằng, nếu giá trị biến thẻ thành viên tăng từ 0 đến 1, thì làm cho odds của y = 1 tăng gấp 2 lần. Như vậy, thẻ thành viên có tác động làm tăng cơ hội khả năng đăng ký ưu đãi. Chúng ta sử dụng odds ratio như một cách để định lượng mối quan hệ giữa biến độc lập và biến mục tiêu trên cơ sở biến mục tiêu là biến định tính.
Nếu Odds ratio thực tế > 1, thì khả năng khách hàng có thẻ thành viên đăng ký ưu đãi cao hơn khách hàng không có thẻ thành viên, và ngược lại, còn nếu Odds ratio = 1, thì khách hàng có hay không có thẻ thành viên sẽ không ảnh hưởng đến khả năng đăng ký ưu đãi.
Tiếp tục, ở trên chúng tôi có nói là odds ratio được tính toán khi một biến thay đổi giá trị còn các biến còn lại giữ nguyên tuy nhiên không có nghĩa là odds ratio chỉ thể hiện ý nghĩa khi giá trị biến còn lại là có định
Cụ thể, quay lại kết quả ở trên, odds ratio = 2.17, vẫn có ý nghĩa và được kết luận tương tự nếu biến số tiền khách hàng chi năm ngoái tăng lên 1 đơn vị, ví dụ là 4 triệu, hay tại bất kể giá trị nào, nói cách khác ở ví dụ trên chúng ta lấy giá trị 3 triệu để tính odds ratio, chúng ta có thể lấy 4 triệu để tính thì kết quả vẫn như vậy. Odds ratio (odds (x1 = 3 vs x2 = 1) / odds (x1 = 3 vs x2 = 0)) sẽ bằng Odds ratio (odds (x1 = 4 vs x2 = 1) / odds (x1 = 4 vs x2 = 0)). Tránh bị nhầm lẫn.
Do đó chúng ta có thể kết luận thẳng là khách hàng có thẻ thành viên sẽ có khả năng đăng ký ưu đãi nhiều hơn khách hàng không có thẻ thành viên mà không cần quan tâm đến số tiền khách hàng đó bỏ ra trong năm ngoái.
Các bạn hãy tự tính odds ratio đối với trường hợp biến số tiền chi ra năm ngoài tức biến x1 thay đổi 1 đơn vị (đơn vị triệu động ví dụ 3 triệu lên 4 triệu) còn x2 giữ nguyên để xem tác động của biến lên odds thể hiện khả năng khách hàng đăng ký ưu đãi nhé!
- Mối liên hệ giữa odds và hệ số hồi quy
Tiếp tục, một ưu điểm nữa mà odds có được chính là thông qua hệ số hồi quy chúng ta có thể ước lượng được chính giá trị odds ratio của một biến sử dụng số hằng số nepe e:
Cụ thể công thức:
Odds(xi) = eβxi
Lấy lại ví dụ ở trên với biến số tiền chi là x1 có hệ số hồi quy β1 là 0.192, biến x2 thẻ thành viên với β2 là 0.771
Odds ratio (biến x1) = e0.192 = 1.211
Odds ratio (biến x2) = e0.771 = 2.16
Chúng ta có thể thấy odds ratio của biến 2 gần bằng kết quả mình tính ở phần 1), nghĩa là dựa trên hệ số hồi quy chúng ta có thể tìm ra giá trị ước lượng odds ratio và kết luận ngay y như phần 1). Còn odds ratio của biến x1, thì phía trên là kết quả các bạn cần tìm cho yêu cầu chúng tôi đề ra cuối phần 1, 1.211 nghĩa là số tiền chi năm ngoái tăng lên 1 triệu thì khả năng đăng ký ưu đại sẽ tăng gấp 1.2 lần. Đây được xem là công thức tính nhanh và cực kỳ hữu ích mà không cần phải tính toán xác suất từ phương trình tìm được, tức mình đã giảm được 2 bước tính: tìm xác suất, tính odds, tính odds ratio.
Một ưu điểm nữa quan trọng khác nữa. Chắc từ nãy giờ sẽ có bạn thắc mắc là tại sao chỉ xét odds ratio cho một biến mà giá trị của nó thay đổi 1 đơn vị mà không phải từ 1 trở lên trong khi các biến còn lại thì giữ nguyên?
Ví dụ nếu số tiền khách hàng chi ra từ 3 triệu tăng lên 6 triệu, tức gấp đôi thì odds ratio sẽ bị tác động như thế nào
Odds ratio (biến x1: 3 triệu à 6 triệu) = e(6 – 3)* 0.192 = 1.78
Nghĩa là khách hàng có số tiền chi ra năm ngoái 6 triệu đồng sẽ có khả năng đăng ký ưu đãi cao gấp 1.78 lần so với khách hàng có số tiền chi ra năm ngoái là 3 triệu bất kể có hay không có thẻ thành viên.
- Ước lượng odds ratio trong thực tế
Như đã nói ở trên thì hầu hết những kết quả suy ra được từ phương trình hồi quy logistic đều chỉ mới dừng lại ở việc ước lượng, chắc chắn sẽ có sai số. Chưa đi qua phần đánh giá độ chính xác của mô hình hồi quy logistic trong việc phân loại và dự báo nhưng chúng ta vẫn có thể đưa ra kết luận về mối quan hệ giữa các biến độc lập lên biến mục tiêu trong tổng thể thông qua ước lượng khoảng tin cậy của odds ratio.
Ước lượng là một phương pháp trong thống kê, qua các tham số mẫu như trung bình mẫu , độ lệch chuẩn mẫu s, tỷ lệ mẫu chúng ta có thể suy luận ra được các tham số tổng thể như trung bình µ, độ lệch chuẩn tổng thể σ, tỷ lệ tổng thể p. Có 2 dạng ước lượng là ước lượng điểm (Point estimation) và ước lượng khoảng (Interval estimation). Ước lượng điểm nghĩa là chúng ta dùng các tham số mẫu ước lượng trực tiếp các tham số tổng thể, không xem xét đến mức độ chênh lệch thực tế. Ví dụ odds ratio = 2.16 và ta lấy kết quả này để kết luận cho tổng thể nghiên cứu thì đây là ước lượng điểm. Nếu chúng ta muốn ước lượng chính xác hơn giá trị của các tham số tổng thể thì phải xây dựng một khoảng số gọi là khoảng ước lượng, và khoảng này có khả năng cao chứa các tham số của tổng thể với một độ tin cậy nhất định, còn gọi là Confidence interval.
Chi tiết phương pháp ước lượng trong thống kê, mời các bạn tham khảo bài viết về thống kê suy luận của chúng tôi:
Tổng quan về Statistics: inferential statistics (thống kê suy luận)
Ước lượng khoảng tin cậy của Odds ratio xét cho mỗi cặp biến độc lập và mục tiêu

Bên trên là công thức tổng quát của ước lượng khoảng. Tuy nhiên đối với odds ratio thì chúng ta không thể làm tương tự như trên, tức tìm cho nó độ lệch chuẩn, rồi đi tìm sai số chuẩn bằng cách lấy độ lệch chuẩn chia cho căn bậc 2 của mẫu và nhân cho giá trị Z tra bảng với độ tin cậy và mức ý nghĩa α. Nhưng odds ratio thực chất là tỷ lệ của 2 odds, và nó không phải là 1 số thực, do đó nó chưa chắc có dạng phân phối chuẩn. (Các bạn có thể xem lại các bài viết của chúng tôi về thống kê để biết thêm nếu mới nghe đến lần đầu các thuật ngữ trên)
Mặt khác phương pháp ước lượng áp dụng cho đối tượng dữ liệu có phân phối chuẩn hoặc xấp xỉ chuẩn. Nhắc lại về phân phối xác suất là gì: để xác định các đại lượng ngẫu nhiên (đối tượng nghiên cứu), chúng ta phải biết được mỗi một đại lượng ngẫu nhiên có thể nhận giá trị nào trong một tập hợp các giá trị, với xác suất tương ứng là bao nhiêu, đây chính là cách chúng ta đang xem xét đến phân phối xác suất cho từng giá trị có thể xảy ra. Phân phối chuẩn là quy luật phân phối áp dụng trong tự nhiên và là quy luật phân phối được dùng nhiều nhất.
Chúng ta phải chuyển giá trị odds ratio thành giá trị số thực bằng cách dùng logarith. Ví dụ chúng ta có bảng dữ liệu dạng bảng tương quan:
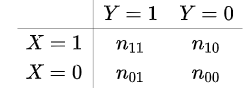
n11 là số quan sát mà tại đó đối tượng dữ liệu có đặc điểm X = 1, và Y = 1, xét tương tự có các n còn lại. Dễ hiểu hơn, lấy lại ví dụ trên, n11 là số khách hàng có thẻ thành viên có đăng ký ưu đãi. Lưu ý bảng được lập từ dữ liệu mẫu lịch sử, giá trị của biến mục tiêu không bị ẩn. Bảng này còn gọi là Contigency table. Nếu X là biến số tiền chi tiêu, và odds ratio tính trên biến này, thì X = 1 (là trường hợp x1 = 4 triệu) X = 0 (là trường hợp x1 = 3 triệu)
Bảng xác suất tương ứng
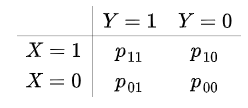
Ví dụ xác suất khách hàng có thẻ thành viên và đăng ký ưu đãi là p11. Lưu ý trên đây mới là giá trị ước lượng.
Odds ratio = (P11/ P01) / (P10/ P00) = [(n11/n)/(n01/n)]/[(n10/n)/(n00/n)]
= (n11*n00/ n10*n01)
Lý do chúng tôi nhắc đến 2 bảng này là vì sai số chuẩn của odds ratio có công thức:
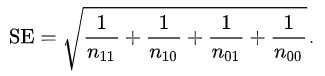
Công thức ước lượng khoảng tin cậy của odds ratio, sau khi sử dụng log để đưa sang phân phối xấp xỉ chuẩn ký hiệu Log(odds ratio) ~ N (log(odds ratio), σ2).:
![]()
Theo thông lệ thì độ tin cậy sẽ là 95%, tra bảng phân phối chuẩn tắc chúng ta có 1.96*SE là giá trị sai số ε cần tìm cho khoảng ước lượng.
Quay lại ví dụ trên, chúng ta sẽ ước lượng khoảng tin cậy cho odds ratio trường hợp có hay không có thẻ thành viên.
Các bạn có thể tải data theo link google drive tại đây.
Sau đó lập bảng contigency để tìm các giá trị n. Kết quả như sau:
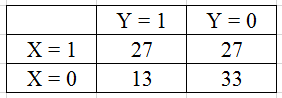
SE = (1/27 + 1/27 + 1/13 + 1/33)^1/2 = 0.43
Log(odds ratio) = log(0.27*0.33/0.13*0.27) = log(2.538) = 0.93
Suy ra 0.93 ± 1.96*0.43 = 0.93 ± 0.8428. Vậy khoảng ước lượng cần tìm (0.0968, 1.765). Tuy nhiên đến đây ta lại phải chuyển ngược về giá trị tỷ lệ của odds ratio, bằng cách dùng hằng số nepe. Lưu ý khi bấm máy tính các bạn đừng làm tròn số để ra kết quả chính xác.
E0.0968 = 1.102 và e1.765= 5.848. Như vậy odds ratio nằm trong khoảng (1.102, 5.848) với độ tin cậy 95%. Kết luận khả năng khách hàng đăng ký ưu đãi nếu có thẻ thành viên sẽ cao gấp từ 1.102 đến 5.848 lần so với khách hàng không có thẻ thành viên, kết luận với độ tin cậy 95%.
Kết quả trong SPSS:
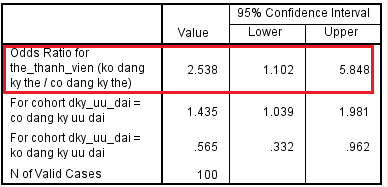
Lưu ý quan trọng nữa, odds ratio trong trường hợp này không vừa có thể < 1 vừa có thể > 1 tức nó hoàn toàn nằm ở một phía nên có thể khẳng định khả năng khách hàng có thẻ thành viên đăng ký ưu đãi có hoàn toàn cao hơn khách hàng không có thẻ thành viên hay không. Suy ra biến thẻ thành viên cũng có thể có ý nghĩa để phân tích ở khía cạnh này. Đây cũng là cơ sở đánh giá phương trình hồi quy logistic có phù hợp để dự báo hay không. Ở phần sau bài viết chúng ta sẽ đi qua phương pháp chủ yếu dùng để đánh giá độ phù hợp của phương trình.
Một thông tin giúp ích muốn gửi đến bạn nào cần tính nhanh ước lượng khoảng odds ratio mà không muốn làm tay. Thì hãy truy cập website dưới đây:
https://select-statistics.co.uk/calculators/confidence-interval-calculator-odds-ratio/
Ước lượng khoảng tin cậy của odds ratio nếu xét theo phương trình
Cụ thì ở phía trên chúng ta tính khoảng tin cậy cho odds ratio chỉ quan tâm duy nhất một cặp biến độc lập là biến thẻ thành viên và biến mục tiêu là biến đăng ký ưu đãi. Hay nói cách khác, phương pháp trên chỉ áp dụng khi chúng ta quan tâm mối quan hệ giữa một biến mục tiêu và một biến độc lập trên cơ sở phân tích odds ratio. Cũng qua đây giải thích cho các bạn sẽ thắc mắc tại sao không dùng kết quả odds ratio ước lượng từ phương trình là 2.17 rồi đưa vào log cộng trừ SE.
Nếu dựa theo phương trình thì chúng ta sẽ có kết quả odds ratio của mỗi biến khác với kết quả odds ratio của chính từng biến đó và dĩ nhiên không thể đưa odds ratio tìm được từ phương trình mà công thức ước lượng ở trên.
Do xét trong phương trình nhiều hơn 2 biến, và việc tính toán khoản ước lượng cho odds ratio khá mất thời gian, do phải áp dụng công thức tính sai số chuẩn cho mẫu theo từng biến, nên chúng ta sẽ dùng kết quả từ phần mềm phân tích, ở đây chúng tôi dùng SPSS, để tìm nhanh kết quả. Các bạn có thể tự tìm hiểu thêm về cách tìm Standard error trong Logistic regression ở những tài liệu khác.
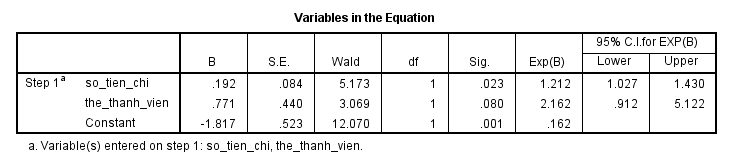
Các bạn nhìn vào cột Exp(B) chính là odds ratio tính bằng cách dùng hằng số nepe cho hệ số hồi quy, hay odds ratio tính được ở trên theo công thức thông thường. Ở cột cuối cùng có lower và upper, thì đây là khoảng tin cậy ước lượng cho odds ratio cần tìm. Xét thử cho biến thẻ thành viên.
Odds ratio lower = e0.192-1.96*0.084 = 1.027; odds ratio upper = e0.192+1.96*0.084 = 1.428
Lúc này chúng ta có thể thấy odds ratio của biến thẻ thành viên nằm trong khoảng (0.912, 5.122) tức có khả năng < 1, và > 1 tức là mặc dù nếu xét trong trường hợp logistic đơn biến, biến thẻ thành viên có ý nghĩa phân tích vì nó tác động làm tăng khả năng khách hàng đăng ký chương trình ưu đãi.
Như vậy, đến đây chúng tôi xin kết thúc phần 3 bài viết về hồi quy logistic. Ở bài viết sắp tới phần 4, chúng ta sẽ đi qua phần quan trọng khác trong hồi quy logistic chính là Maximum likelihood method trong việc ước lượng hệ số hồi quy, với các phương pháp đánh giá độ phù hợp của phương trình hồi quy logistic, cũng như phương pháp đánh giá độ chính xác của mô hình trong việc dự báo giá trị biến mục tiêu y.
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English