Ở các bài viết trước về hồi quy logistic chúng ta đã tìm hiểu sâu hơn về phương trình tổng quát, giải thích hệ số hồi quy, phân tích mối quan hệ giữa các biến độc lập x (hay còn gọi là các yếu tố tác động), với biến mục tiêu y là biến định tính (hay còn gọi là đối tượng nghiên cứu) dựa trên odds và odds ratio, đồng thời thông qua phương trình ước lượng xác suất thể hiện khả năng y = 1, với 1 được gán cho sự kiện xảy ra mà chúng ta quan tâm. Trong bài viết phần 4 lần này, chúng tôi sẽ trình bày về phương pháp xác định tham số (hệ số hồi quy) – Maximum likelihood Estimation một cách dễ hiểu nhất, sau đó là sẽ tìm hiểu phương pháp kiểm định đánh giá độ phù hợp ban dầu của phương trình trong việc dự báo giá trị của biến mục tiêu y phổ biến nhất là Wald test, Likelihood Ratio test. Trong bài viết này chúng ta quan tâm trước về Wald test.
Một vài nội dung trong bài viết có tham khảo trong tài liệu Applied Logistic Regression của tác giả David W. Hosmer, Stanley Lemeshow Rodney và X. Sturdivant.
Các bạn nào chưa tham khảo các bài viết trước của chúng tôi về hồi quy logistic, hay chưa biết gì về công cụ phân tích này thì sẽ khó nắm bắt nội dung trong phần 4.
Tổng quan về Logistic regression (hồi quy Logistic) (Phần 1)
Tổng quan về Logistic regression (hồi quy Logistic) (Phần 2)
Tổng quan về Logistic regression (hồi quy Logistic) (Phần 3)
Nhắc lại một sô điểm quan trọng về hồi quy logistic
Hồi quy logistic áp dụng cho phân tích mối quan hệ giữa các biến độc lập và biến mục tiêu y, trên cơ sở biến y là biến định tính có 2 hay nhiều giá trị (chúng ta đang tập trung vào Binary logistic regression áp dụng cho biến y có 2 giá trị định tính). Kết quả của phương trình hồi quy logistic hướng đến ước lượng hay dự báo xác suất thể hiện khả năng đối tượng nghiên cứu được phân loại là một trong các giá trị của biến mục tiêu y. Phương trình tổng quát:
Phương trình hồi quy logistic đơn biến:
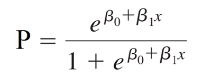
Phương trình tổng quát của hồi quy logistic
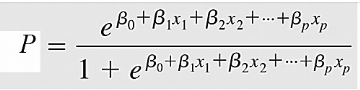
Phương trình chuyển đổi của hồi quy logistic (logit transformation)
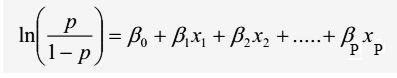
Với p là xác suất khả năng y xảy ra 0 hoặc 1 (chịu ảnh hưởng của biến x), là biến chúng ta sẽ dự báo giá trị, x là biến độc lập (biến tác động lên biến phụ thuộc). β0 là giá trị ước lượng cho p khi x đạt giá trị 0, β1 dùng để xác định giá trị trung bình của p tăng hay giảm khi x tăng nhưng luôn được giới hạn trong khoảng 0 đến 1, hay β1 là giá trị ước lượng sự khác biệt giữa tác động của biến độc lập lên biến mục tiêu (xác suất) khi giá trị của giữ nguyên hoặc thay đổi 1 đơn vị (theo công thức ước lượng odds ratio dưới dây)
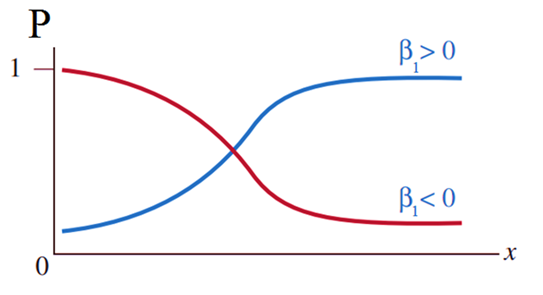
Lưu ý cực kỳ quan trọng: giá trị 0 và 1 của y không phải giá trị số thực, mà là kết quả mã hóa (coding) của những giá trị định tính của biến y, ví dụ y = 0 nghĩa là đối tượng nghiên cứu trong tương lai có thể “không mua hàng”, “đã rời dịch vụ”, “nợ xấu”, y = 1 thì suy ngược lại.
Công thức odds và odds ratio:
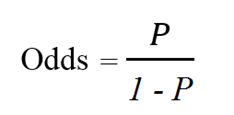
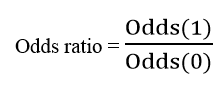
Odds ratio là tỷ lệ của khả năng xảy ra sự kiện A (Odds(1)) khi sự kiện B đã xảy ra và khả năng xảy ra của sự kiện A khi không có sự kiện B (Odds(0)), hoặc ngược lại, tỷ lệ của khả năng xảy ra sự kiện B khi sự kiện A xảy ra và khả năng xảy ra sự kiện B khi không có sự kiện A. Hai sự kiện là độc lập khi và chỉ khi Odds ratio bằng 1, tức là khả năng xảy ra của các sự kiện là như nhau. Nếu Odds ratio lớn hơn 1, thì A và B tương quan thuận với nhau sự hiện diện của B làm tăng khả năng xảy ra sự kiện A và hoặc ngược lại, nếu Odds ratio nhỏ hơn 1, thì A và B có mối tương quan ngược chiều và sự hiện diện của một sự kiện sẽ làm giảm khả năng xảy ra của sự kiện khác.
Trong đó:
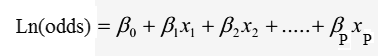

Khác với hồi quy tuyến tính thông thường, chúng ta chỉ quan tâm đến hệ số tương quan, hệ số hồi quy, hệ số xác định R2 thì trong hồi quy logistic để tìm hiểu và phân tích sâu mối quan hệ giữa các biến, chúng ta phải nắm rõ xác suất, odds, odds ratio, và phương trình tổng quát theo dạng logit hoặc chuyển đổi (logit transformation). Để hiểu rõ hơn về odds và odds ratio các bạn hãy xem lại bài viết phần 3 của chúng tôi theo link ở trên.
Maximum Likelihood Estimation (MLE)
Trước khi đi qua phương pháp Maximum likelihood Estimation trong logistic regression, chúng ta quay lại một chút với phương pháp ước lượng tham số trong hồi quy tuyến tính,linear regression để tìm hiểu sự khác biệt nữa giữa 2 dạng hồi quy này. Lưu ý bài viết không đi sâu vào cách giải bài toán MLE, chỉ trình bày khái niệm tổng quát để các bạn hiểu rõ bản chất.
Đối với hồi quy tuyến tính, biến mục tiêu y là biến định lượng và giá trị dự báo hay ước lượng của biến y là giá trị số thực. Do đó điều quan tâm nhất khi xây dựng và đánh giá mô hình hồi quy tuyến tính đó chính là làm sao giảm được sai số một cách nhỏ nhất giữa kết quả thực tế và kết quả dự báo hay ước lượng của y. Phương pháp được dùng để xác định tham số, hay các hệ số hồi quy β sao cho thỏa mãn yêu cầu trong hồi quy tuyến tính chính là Least Squares Principle, phương pháp bình phương bé nhất.
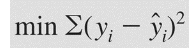
Giải thích một cách đơn giản nhất. Giả sử chúng ta có một tập dữ liệu có các giá trị x và giá trị y tạo thành rất nhiều điểm dữ liệu trên đồ thị, và qua các điểm này chúng ta có thể vẽ rất nhiều đường thẳng tuyến tính thể hiện mối quan hệ tuyến tính giữa biến x và y, tuy nhiên chúng ta chỉ có thể chọn được 1 đường thẳng thể hiện tốt nhất mối quan hệ này, tương ứng như việc chúng ta chỉ lập được một phương trình hồi quy tuyến tính duy nhất. Tiêu chí nào để chọn lựa? Chúng ta sẽ dựa trên sai số của giá trị y dự báo và y thực tế, nếu sai số của phương trình nào nhỏ nhất thì phương trình ấy sẽ được chọn.
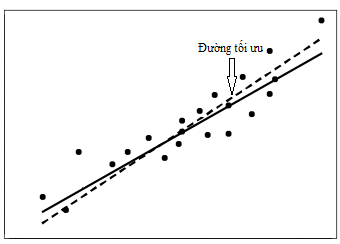
Khác với hồi quy tuyến tinh, hồi quy logistic hướng đến ước lượng xác suất khả năng y đạt giá trị 0 hoặc 1 vói 1 gán cho sự kiện xảy ra, hay kết quả phân loại của đối tượng nghiên cứu mà chúng ta quan tâm. Do đó, khi kết quả ước lượng từ phương trình là xác suất, và kết quả sau cùng của biến y là kết quả định tính, thì phương pháp bình phương bé nhất không còn phù hợp mặc dù vẫn trên cơ sở là tối thiểu sai sót trong việc dự báo. Maximum Likelihood Estimation (MLE), một kỹ thuật xác định tham số trong phân tích hồi quy, được ưu tiên chọn lựa cho trường hợp mô hình hồi quy với biến y là biến định tính và dựa vào dữ liệu có sẵn, với các quan sát, các đối tượng nghiên cứu đã có sẵn giá trị cụ thể tại biến mục tiêu.
Chúng ta cùng đi qua giải thích tên gọi của phương pháp. Chữ Estimation thể hiện giá trị các hệ số hồi quy β tìm được trong phương trình tổng quát chỉ là ước lượng tạm thời không chính xác hoàn toàn trong thực tế, do đó luôn có sai số nhất định, và để chính xác hơn sau khi tìm được hệ số hồi quy thông qua Maximun Likelihood Estimation, chúng ta có thể xây dựng khoảng tin cậy (Confidence Interval) giống như odds ratio ở bài viết trước. Chữ Maximum có nghĩa là tối đa, Likelihood nghĩa là khả năng xảy ra, gộp chung thì được hiểu các tham số hay hệ số hồi quy được tìm thấy phải tối đa khả năng y xảy ra một trong các sự kiện, hoặc khả năng cao được phân loại là một trong các giá trị có sẵn.
Nói cách khác, MLE là phương pháp dự đoán tham số của một mô hình dựa trên những “quan sát” có sẵn (observed data), thông qua việc tìm kiếm một bộ những tham số/ hệ số hồi quy sao cho có thể tối đa hoá khả năng mà mô hình đó sinh ra các “quan sát” có sẵn.
Với Least squares method để tối thiểu sai số, còn Maximum Likelihood Estimation để tối đa khả năng y đạt được một kết quả cụ thể, có thể là kết quả mà chúng ta quan tâm khi nghiên cứu ví dụ y = 1 – khả năng rời dịch vụ.
Giải thích dễ hiểu hơn giả sử gán y = 1 cho khách hàng rời dịch vụ vì sẽ ảnh hưởng mạnh lên doanh thu, chúng ta sẽ muốn tìm hiểu kỹ hơn những yếu tố nào và chúng đã tác động như thế nào đến khả năng khách hàng rời dịch vụ như một cách bao quát hết vấn đề cần khắc phục. Cụ thể chúng ta sẽ muốn biết để xác suất cao nhất khiến y = 1, thì phương trình hồi quy sẽ gồm các biến độc lập nào với các hệ số hồi quy tương ứng nào sẽ thỏa mãn.
Maximum Likeliehood Estimation là phương pháp xác định các hệ số hồi quy trên mô hình xây dựng cho cả bộ dữ liệu có sẵn, sao cho tất cả các đối tượng nghiên cứu đồng thời đạt những giá trị cụ thể tại biến mục tiêu (ví dụ có thể y = 1 hay y = 0) với xác suất xảy ra đồng thời là cao nhất. Chúng ta biết các quan sát trong tập dữ liệu đã mang giá trị gì ở biến mục tiêu, biết các biến độc lập và biến mục tiêu có mối quan hệ ra sao được mô tả bởi các hệ số hồi quy cụ thể, chúng ta phải tìm các hệ số hồi quy như cách xác định nguyên nhân dẫn đến các kết quả đã có sẵn, đặc biệt nguyên nhân đó phải tác động mạnh nhất hay khiến cho xác suất xảy ra đồng thời là cao nhất. Likelihood chính là tên gọi của phương pháp tính xác suất đồng thời (likelihood function)
Giả sử chúng ta có một bộ dữ liệu bao gồm các điểm dữ liệu X1, X2, X3,… XP, p = 1, 2, 3,…n mỗi điểm dữ liệu có thể mô tả mối quan hệ giữa y và các biến x trên đồ thị, mỗi điểm là một sự kiện đã xảy ra, và một bộ các hệ số hồi quy ký hiệu β = (β0, β1, β2,… βP). Lưu ý ở đa phần những tài liệu khác, bộ tham số thường được ký hiệu là θ. Nhưng trong phần giải thích chi tiết về MLE, chúng tôi sẽ sử dung ký hiệu β vì nó giống ký hiệu hệ số hồi quy mà thôi, thực chất thì 2 ký hiệu này không thể hiện ý nghĩa khác nhau, và các hệ số hồi quy chính là các tham số của một phương trình tổng quát.
P(X1׀β) là xác suất xuất hiện điểm dữ liệu X1 hay sự kiện X1 xảy ra khi mô hình đã xác định bộ tham số β, tương tự X2, X3. Như đã nói chúng ta phải xác định bộ tham số xác suất xảy ra đồng thời của tất cả các sự kiện là cao nhất, với P(X1, X2, X3,…XP ׀β) là xác suất xảy ra đồng thời
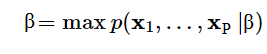
Để giải bài toán Maximum Likelihood Estimation, chúng ta phải tìm ra quy luật phân phối xác suất cho các điểm dữ liệu sao cho xác suất xảy ra đồng thời của chúng là cao nhất. Ngoài ra, trên cơ sở giả định các điểm dữ liệu hay các sự kiện là độc lập với nhau, công thức tính xác suất xảy ra đồng thời sẽ bao gồm tích các xác suất P(X1׀β), P(X2׀β),… đều là các xác suất có điều kiện. Công thức khi đưa về hàm Likelihood
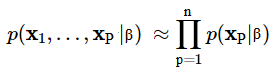
Như vậy để tìm bộ tham số khiến xác suất xảy ra đồng thời lớn nhất chúng ta phải giải bài toán tổng quát sau:
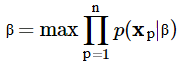
Trên cơ sở tìm xác suất xảy ra đồng thời là lớn nhất để xác định bộ hệ số hối quy β các chuyên gia thường đưa bài trên vào hàm logarith, với hàm logarith, khi X tăng thì Y sẽ tăng, giá trị hàm log đạt tối đa thì biểu thức sẽ tiến đến lớn nhất.
Lưu ý theo công thức logarith, log của một tích sẽ bằng tổng các log đơn lẻ.
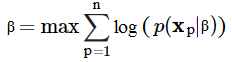
Quay lại với quy luật phân phối xác suất. Phân phối xác suất là gì?
Xác suất hiểu đơn giản là một thước đo, định lượng khả năng xảy ra của một sự kiện nào đó. Xác suất luôn được giới hạn trong giá trị từ 0 đến 1, xác suất càng gần 0 thì khả năng xảy ra sự kiện đó ngày càng thấp, và ngược lại. Để xác định các đại lượng ngẫu nhiên, chúng ta phải biết được mỗi một đại lượng ngẫu nhiên có thể nhận giá trị nào trong một tập hợp các giá trị, với xác suất tương ứng là bao nhiêu, đây chính là cách chúng ta đang xem xét đến phân phối xác suất cho từng giá trị có thể xảy ra.
Trong các quy luật phân phối xác suất, chúng ta có quy luật phân phối nhị thức (Binominal Distribution hay Bernoulli Distribution), quy luật phân phối Poisson, và quy luật phân phối chuẩn (Normal Distribution hay Gaussian Distribution) là những quy luật phân phối thông dụng, trong đó phân phối chuẩn là phổ biến nhất.
Cụ thể các quy luật xác suất này là gì mời các bạn theo dõi bài viết thống kê suy luận của chúng tôi theo link tại đây:
Tổng quan về statistics: Inferential statistics (thống kê suy luận)
Một quy luật phân phối chính nó cũng được đặc trưng bởi các tham số nhất định như µ là giá trị trung bình (Mean), σ là độ lệch chuẩn (Standard deviation), E(x) kỳ vọng (bằng trung bình nếu x là biến định lượng rời rạc). Như vậy chúng ta phải tìm ra quy luật phân phối xác suất sao cho xác suất xảy ra đồng thời của các sự kiện X1, X2, X3,… XP là cao nhất, và từ đó tìm ra các tham số đặc trưng của quy luật, rồi xác định các hệ số hồi quy tương ứng. Lưu ý cỡ mẫu cũng là một yếu tố tác động lên các đặc trưng của quy luật phân phối.
Ví dụ các điểm dữ liệu X1, X2, X3,… XP có phân phối chuẩn với µ là giá trị trung bình (Mean), σ là độ lệch chuẩn (Standard deviation), hàm mật độ xác suất như sau:
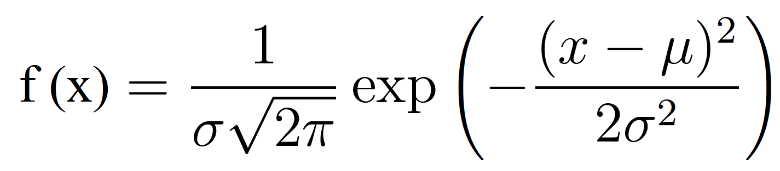
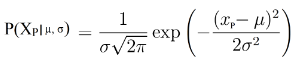
Công thức tính xác suất đồng thời bằng cách lấy tích các xác suất đơn lẻ
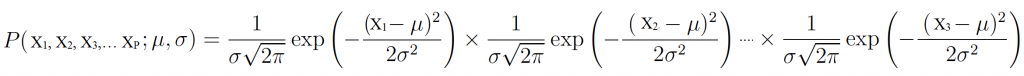
Chuyển sang hàm logarith, lưu ý ở đây là logarith tự nhiên:
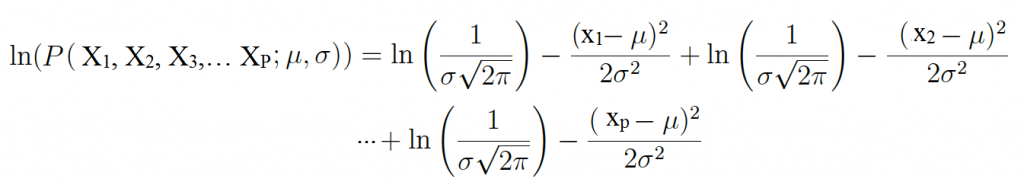
Tiếp tục áp dụng các công thức toán học như đạo hàm để tìm µ, và σ và suy ra các hệ số hồi quy. Các bạn có thể tự tìm hiểu thêm ở những tài liệu khác.
Ngoài ra giả sử chúng ta có các mô hình hồi quy logistic, mỗi mô hình có một bộ hệ số hồi quy khác nhau, chúng ta sẽ cần chọn ra mô hình có phân phối chuẩn mà tại đó xác suất thể hiện khả năng các sự kiện xảy ra đồng thời là cao nhất. Ví dụ như qua đồ thị dưới đây:
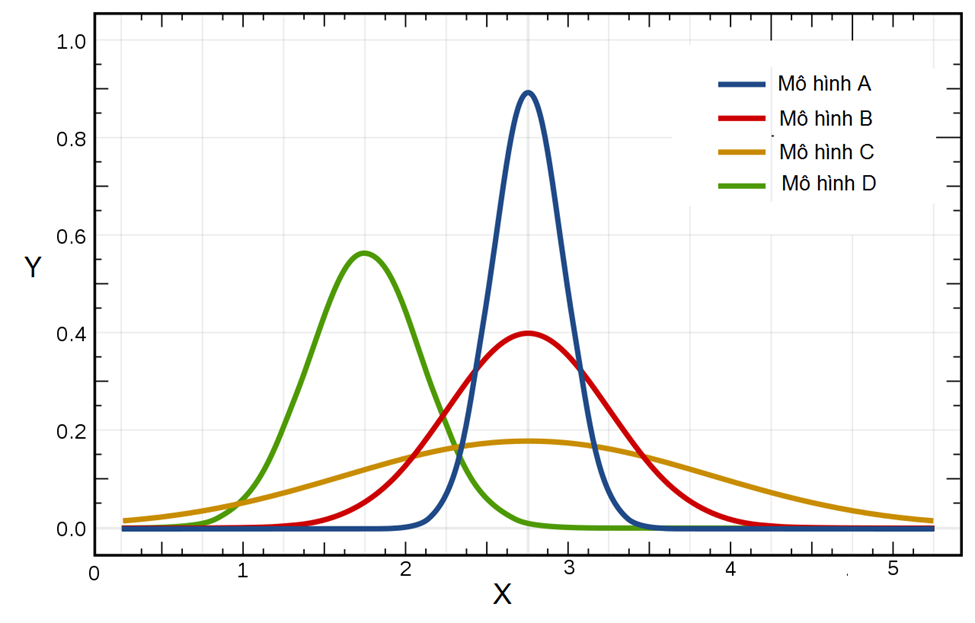
Thông qua đồ thị chúng ta thấy mô hình A là phù hợp hợp nhất.
Mặc dù phân phối chuẩn là phân phối phổ biến hay được xét đến nhưng khi nói đến likelihood hay log – likelihood, người ta thường quan tâm nhiều hơn về phân phối nhị thức Binomal Distribution. Công thức tông quát của phân phối nhị thức
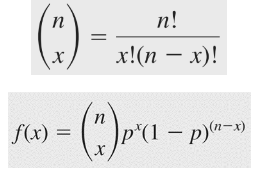
Giá trị trung bình của X: µ = n*p
Phương sai của X: σ2 = n*p*q
Giả sử chúng ta tiến hành tung đồng xu có 2 mặt, cho dù tung bao nhiêu lần thì chúng ta cũng chỉ được 2 kết quả là mặt trên và mặt dưới của đồng xu. Tương tự như bạn thi một cuộc thi chỉ có 2 kết quả đậu và rớt, hay dự án công ty chỉ có thành công hay thất bại.
Gọi A là kết quả xảy ra (thành công) hoặc A không xảy ra (không thành công), giống như khả năng khách hàng rời hay không rời dịch vụ. Ở mọi phép thử xác suất để A xảy ra phải luôn bằng một hằng số p và xác suất để A không xảy ra là q = 1 – p. Chúng ta cho X là số lần A xảy ra trong n phép thử, vậy X nhận giá trị từ 0, 1, 2, …, n, và xác suất tính được theo công thức Bernoulli. Đây gọi là quy luật phân phối nhị thức ký hiệu X~B(n,p) với n là số phép thử, p là xác suất để một trong hai kết quả xảy ra. x là số phép thử thành công trong tập dữ liệu hay nói cách khác là số lần sự kiện chúng ta quan tâm xảy ra.
Công thức likelihood theo quy luật phân phối nhị thức, với P là xác suất cho sự kiện mong muốn xảy ra hay y = 1, 1 – P là xác suất xảy ra khi y = 0. Với Y1, Y2,…Yn là số quan sát có trong tập dữ liệu và độc lập với nhau. Chúng ta có hàm likelihood như sau
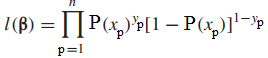
Chuyển sang hàm log như đã nói ở trên mục đích là tìm hệ số hồi quy sao cho xác suất xảy ra đồng thời của tất cả các sự kiện là cao nhất, trường hợp ở đây chỉ có Yp = 0, Yp = 1. Đây chính là log likelihood cần tìm:
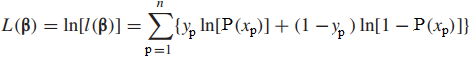
Nếu chúng ta có x là tổng số quan sát có Y = 1 tức nhiều sự kiện quan tâm xảy ra, n là cỡ mẫu tổng số quan sát có Y = 1, và kể cả Y = 0. Chúng ta có công thức likelihood tổng quát như sau:
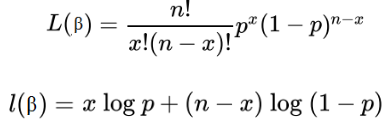
Chúng ta phải tìm giá trị p sao cho biểu thức đạt giá trị lớn nhất.
Đến đây cũng giống như trong phân phối chuẩn chúng ta sẽ áp dụng các công thức toán học phù hợp để tìm ra các đặc trưng của phân phối và những hệ số hồi quy.
Về các quy luật phân phối xác suất còn lại trong tính toán MLE, các bạn có thể tham khảo thêm tại blog Machine learning cơ bản của tác giả Vũ Hữu Tiệp, Tiến sĩ ngành Machine Learning and Computer Vision tại Đại học bang Pennsylvania, Hoa Kỳ theo đường link dưới đây. Nội dung hoàn chỉnh và đầy đủ nhất mặc dù có lẽ phức tạp hơn nhưng sẽ cực kỳ dễ hiểu đối với những bạn giỏi về toán học vì bài viết trình bày khá chi tiết cách giải.
Link bài blog của tác giả https://machinelearningcoban.com/2017/07/17/mlemap/
Lưu ý nữa, ở các bài viết trước khi các hệ số hồi quy được tìm thấy chúng ta vẫn giữ nguyên ký hiệu β nhưng trong một số tài liệu về thống kê, cũng như phân tích hồi quy khi các kết quả có được là các kết quả ước lượng không phải chính xác trong thực tế thì có thêm ký hiệu “^” ở trên đầu.
Như vậy đến đây kết thúc phần giới thiệu sơ lược về Maximum Likelihood Estimation, hi vọng các bạn sẽ hiểu được phần nào về mảng kiến thức này. Thông thường nếu chúng ta áp dụng công cụ phân tích dữ liệu để tìm ra phương trình hồi quy logistic thì ít khi nào quan tâm đến phương pháp này, nhưng hiểu thêm về nó cũng là một cách hiểu thêm về logistic regression.
Về cách diễn giải phương pháp, thì có thể khẳng định với các bạn, không có sự giống nhau nhất định, các tài liệu khác nhau về hồi quy logistic hay regression tổng thể sẽ có thể giải thích theo nhiều hướng khác nhau tùy theo góc nhìn của chuyên gia phân tích, đơn giản hay phức tạp. Nhưng tất cả đều có một điểm chung, chính là làm sao để tối đa xác suất khả năng biến mục tiêu y đạt được một giá trị cụ thể hay xác suất để một sự kiện xảy ra là cao nhất.
Phương pháp kiểm định trong hồi quy logistic
Đến mỗi lần kiến thức về kiểm định được nhắc đến, chúng ta phải quan tâm là tại sao cần phải làm kiểm định, phương pháp kiểm định là gì?
Kiểm định giả thuyết (Hypothesis Test) là một trong những kiến thức nền tảng, và quan trọng nhất trong lĩnh vực thống kê (Statistics), được sử dụng để đánh giá liệu các giả thuyết từ dữ liệu mẫu có thể suy ra dữ liệu tổng thể nghiên cứu được hay không. Nói cách khác dựa trên các tham số, đặc trưng của mẫu, các kết luận đưa ra về quy luật phân phối, các đặc trưng của tổng thể có hợp lý hay không. Trong phân tích hồi quy cũng vậy, chúng ta thông thường không có dữ liệu của tổng thể nghiên cứu, chỉ có tập dữ liệu mẫu, mặc khác khi tiến hành xây dựng mô hình trên tổng là rất phức tạp và tốn kém cả về thời gian và chi phí, nên để kiểm chứng các kết quả từ dữ liệu mẫu có suy ra được cho tổng thể hay không thì cần dùng đến kiểm định.
Kiểm định thường là quy trình sau cùng của bước tính toán các tham số, thiết lập phương trình tổng quát và ước lượng tham số trong khoảng tin cậy nhất định nhưng là quy trình ban đầu đánh giá độ hiệu quả của mô hình hồi quy. Nói cách khác, kiểm định là đánh giá ý nghĩa các hệ số hồi quy, ý nghĩa của các biến độc lập trong phương trình, và ý nghĩa của phương trình tổng quát trong việc đưa ra dự báo, ước lượng giá trị của biến mục tiêu trong tổng thể ở tương lai.
Lưu ý quan trọng, nếu kiểm định là phương pháp ban đầu đánh giá độ phù hợp của mô hình hồi quy logistic thì các phương pháp kiểm tra độ chính xác của mô hình hồi quy logistic trong việc dự báo là phương pháp đánh giá độ hiểu quả cuối cùng, giống như cú “chốt hạ” xem mô hình có được áp dụng trong thực tế hay không.
Logistic Regression bản chất là một kỹ thuật dự báo, phân loại đối tượng dữ liệu gần giống như cây quyết định (Decision trees) hay còn gọi là một phương pháp Classification Technique. May mắn, chúng tôi đã có sẵn một bài viết về Evaluation Classification cho những bạn nào quan tâm và muốn tìm hiểu trước qua link dưới đây. Trong bài viết tới chúng tôi sẽ trình bày lại vì các phương pháp này phải gắn với ví dụ phức tạp thì mới hiểu được. Ngoài ra còn các phương pháp khác bên cạnh các phương pháp Classification model evaluation áp dụng cho hồi quy logistic như các phương pháp Goodness of fit sẽ được chúng tôi trình bày ở bài viết tiếp theo về ứng dụng cụ thể của hồi quy logistic.
Phương pháp đánh giá mô hình phân loại (Classification model evalutation)
Khi xây dựng một mô hình hồi quy, cho dù là logistic hay linear có lẽ chúng ta đều quan tâm là các biến độc lập và biến mục tiêu có quan hệ như thế nào, bền vững hay không bền vững, mạnh hay yếu, và những mối quan hệ này có ý nghĩa phân tích không?
Các phương pháp kiểm định sẽ cho ta câu trả lời ban đầu cho những vấn đề trên mà chúng ta quan tâm. Hai phương pháp kiểm định phổ biến trong hồi quy logistic chính là Wald-test và Likelihood Ratio test. Likelihood ratio test phức tạp hơn vì nó có liên quan đến bước chọn lựa biến thích hợp nên chúng tôi sẽ trình bày ở bài viết tới cùng với các phương pháp Goodness of fit hay Classification model evaluationnhư đã nói ở trên.
Wald – test
Nếu các bạn nào đã thao khảo bài viết của chúng tôi về hồi quy đa biến thì cũng biến đến kiểm định t, kiểm định có hay không có mối quan hệ giữa từng biến độc lập và biến mục tiêu, như một cách đánh giá xem biến độc lập này có phù hợp để đưa vô mô hình. Công thức Wald – test giống như công thức kiểm định t. Với βp = 0 nghĩa là biến độc lập và biến phụ thuộc không có mối quan hệ với nhau
Chúng ta có thể đặt các giả thuyết như sau:
H0: βp = 0
H1: βp ≠ 0
Công thức tổng quát:
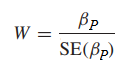
βP là hệ số hồi quy ước lượng được bằng phương pháp MLE, hay nói cách khác là hệ số hồi quy của biến XP tìm được trong phương trình ước lượng Logistic regression. Còn SE là sai số chuẩn của hệ số hồi quy.
Trong một số phần mềm thống kê thì W2 = Z2 (Wald test giống với kiểm định Z trên cơ sở βP là hệ số hồi quy ước lượng trung bình và, SE của βP chính là độ lệch chuẩn), tức bình phương tỷ số ở trên với cơ sở giả thuyết H0 tuân theo phân phối chi bình phương, với bậc tự do là 1 nếu xét cho từng biến độc lập.
Nếu cỡ mẫu lớn hơn 30 (thông thường trong thực tế cỡ mẫu chúng ta lấy sẽ nhiều hơn 30) thì đưa về kiểm định Z và tra bảng phân phối chuẩn Z để kết luận kết quả kiểm định với mức ý nghĩa cho trước, còn nếu cỡ mẫu nhỏ hơn 30, thì đưa về kiểm định t, và tra bảng phân phối t.
Cơ sở bác bỏ giả thuyết chúng ta có thể dựa trên kết quả tra bảng và kết quả kiểm định, nếu kết quả kiểm định > kết quả tra bảng, ngoài ra cũng dựa vào p-value để xét. Nếu xét trên giá trị p-value, bác bỏ H0 khi p-value < α. (p-value là mức ý nghĩa nhỏ nhất mà tại đó H0 bị bác bỏ).
Lấy lại ví dụ của các bài viết trước, các bạn tham khảo lại các bài viết của chúng tôi theo đường link phía trên để nắm chi tiết về ví dụ:
Chúng ta có phương trình hồi quy logistic dự báo khả năng khách hàng đăng ký đăng ký ưu đãi:
E(y) = P = (e(-1.817 + 0.192*x1 + 0.771*x2))/ (1 + e(-1.817 + 0.192*x1 + 0.771*x2))
Biến mục tiêu là khả năng đăng ký chương trình ưu đãi với y = 1 – sẽ đăng ký chương trình, y = 0 – không đăng ký chương trình. Biến độc lập x1 là số tiền khách hàng bỏ ra trong năm vừa rồi (đơn vị triệu VND). Biến độc lập x2 là thông tin về đăng ký thẻ thành viên, x2 = 1 là có thể thành viên, x2 = 0 là không có thể thành viên.
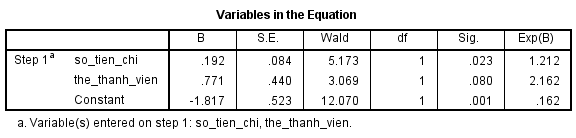
Kết quả từ SPSS cho kết quả kiểm định Wald cho từng biến, bậc tự do là 1, mức ý nghĩa là 0.05 chúng ta có P-value (tại sột Sig.) của biến số tiền chi năm ngoái < 0.05 nên bác bỏ giả thuyết H0 β1 = 0, tức kết luận có mối quan hệ giữa số tiền chi trong năm ngoái và khả năng đăng ký chương trình ưu đãi.
Tính thử: W = [(0.192)/ (0.084)]2 = 5.22 (lưu ý số đã được làm tròn nên kết quả có thể bị chênh lệch, theo chính xác SPSS thì là 0.192024 và 0.084428). W tra bảng là 3.841, mức ý nghĩa là 0.05, bậc tự do là 1. W > W tra bảng, kết luận bác bỏ H0 tương tự.
Các bạn có thể tra bản phân phối chi bình phương để tìm p-value với W là giá trị kiểm định, bậc tự do là 1, hoặc sử dụng hàm trong excel để tìm nếu không có SPSS.
Đối với biến thẻ thành viên, thì ở bài viết trước thông qua odds ratio chúng ta nhận định rằng thẻ thành viên không có tác động lên khả năng khách hàng đăng ký chương trình, lần nữa qua kiểm định Wald test kết quả P-value > 0.05, tức không bác bỏ H0 nghĩa là kết luận không có mối quan hệ giữa biến này với biến mục tiêu.
Kết thúc bài viết phần 4 tại đây, ở bài viết cuối cùng sắp tới chúng ta sẽ đi vào một ứng dụng điển hình của logistic regression với ví dụ phức tạp hơn để trình bày phương pháp kiểm định phức tạp khác là Likelihood ratio, các phương pháp Goodness of fit, và phương pháp đánh giá mô hình phân loại áp dụng cho hồi quy logistic.
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English