Ở bài viết trước tổng quan về hồi quy logistic phần 4 chúng ta đã tìm hiểu về phương pháp Maximum Likelihood Estimation là cơ sở để ước lượng các hệ số hồi quy phục vụ xây dựng phương trình ước lượng hay dự báo xác suất dẫn đến khả năng biến mục tiêu y là biến định tính nhận được một trong các giá trị cụ thể. Đồng thời chúng ta cũng đã tìm hiểu qua công thức kiểm định đầu tiên là Wald test để đánh giá ý nghĩa của hệ số hồi quy hay nói cách khác một biến độc lập hoặc yếu tố có mối quan hệ với biến mục tiêu hay không.
Tiếp tục phần 5, phần cuối trình bày tổng quan về những kiến thức quan trọng trong hồi quy logistic, chúng ta sẽ tiếp tục bàn luận về những công thức đánh giá độ hiệu quả, sự phù hợp của mô hình hồi quy (Goodness of fit) trong dự báo nhưng trước hết giới thiệu lại hồi quy logistic một cách tóm tắt cho bạn nào chưa biết, và tiếp tục 2 phương pháp kiểm định khác ngoài Wald test là Likelihood ratio test, Score test (giới thiệu sơ) và ước lượng khoảng tin cậy cho hệ số hồi quy (khác với ước lượng cho odds ratio). Bài viết này sẽ chỉ giải thích lý thuyết, bài viết sắp tới về ứng dụng chúng ta sẽ đi vào ví dụ cụ thể. Một số nội dung trong bài viết có tham khảo trong tài liệu Applied Logistic Regression của tác giả David W. Hosmer, Stanley Lemeshow Rodney và X. Sturdivant.
Dành cho những bạn chưa tham khảo các bài viết trước:
Tổng quan về Logistic regression (hồi quy Logistic) (Phần 1)
Tổng quan về Logistic regression (hồi quy Logistic) (Phần 2)
Tổng quan về Logistic regression (hồi quy Logistic) (Phần 3)
Tổng quan về Logistic regression (hồi quy Logistic) (Phần 4)
Nhắc lại một vài kiến thức quan trọng (tóm tắt ngắn)
Hồi quy logistic dạng binary là dạng phân tích hồi quy áp dụng để nghiên cứu mối quan hệ giữa các biến độc lập (yếu tố tác động) và biến mục tiêu (đối tượng nghiên cứu) dựa vào đó để đưa ra các kết quả dự báo chính xác. Công thức tổng quát cho hồi quy logistic đơn biến:
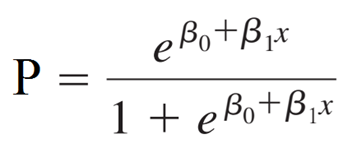
Công thức tổng quát cho đa biến:
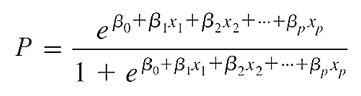
Công thức dạng chuyển đổi (logit transformation) thành hồi quy tuyến tính:
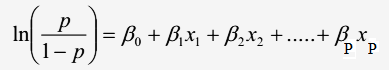
Với p là xác suất khả năng y xảy ra 0 hoặc 1 (chịu ảnh hưởng của biến x), là biến chúng ta sẽ dự báo giá trị, x là biến độc lập (biến tác động lên biến phụ thuộc). β0 là giá trị ước lượng cho p thông qua cơ số e khi x đạt giá trị 0, β1 dùng để xác định giá trị trung bình của p tăng hay giảm khi x tăng nhưng luôn được giới hạn trong khoảng 0 đến 1, hay β1 là giá trị ước lượng sự khác biệt giữa tác động của biến độc lập lên biến mục tiêu (xác suất) khi giá trị của giữ nguyên hoặc thay đổi 1 đơn vị.
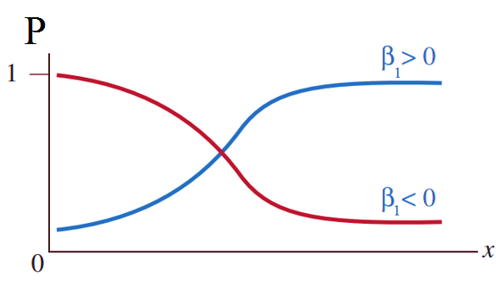
Odds thể hiện khả năng một sự kiện có thể xảy ra bằng cách lấy tỷ lệ xác suất xảy ra chia cho xác suất không xảy ra. Odds ratio là tỷ lệ của khả năng xảy ra sự kiện A (Odds(1)) khi sự kiện B đã xảy ra và khả năng xảy ra của sự kiện A khi không có sự kiện B (Odds(0)), hoặc ngược lại, tỷ lệ của khả năng xảy ra sự kiện B khi sự kiện A xảy ra và khả năng xảy ra sự kiện B khi không có sự kiện A.
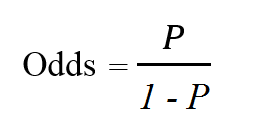
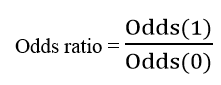
Mối quan hệ giữa odds ratio và hệ số hồi quy của một biến độc lập:
![]()
Likelihood Function cho Logistic regression dạng binary trên giả định các quan sát có phân phối nhị thức với Yp = 0 hay Yp = 1, X1, X2, … Xp là các đối tượng nghiên cứu, n là tổng số quan sát, Pxp là xác suất Yp = 1 hay Yp = 0 tại xp.
Hàm log likelihood trong Maximum likelihood estimation
Tìm hiểu thêm về cách ước lượng khoảng cho odds ratio, và Maximum likelihood estimation các bạn xem lại các bài viết trước, link chúng tôi để đầu bài viết.
Kiểm định Wald – test
Công thức Wald – test giống như công thức kiểm định t. Với βp = 0 nghĩa là biến độc lập và biến phụ thuộc không có mối quan hệ với nhau
Chúng ta có thể đặt các giả thuyết như sau:
H0: βp = 0
H1: βp ≠ 0
Công thức tổng quát:
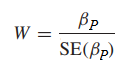
Trong một số phần mềm thống kê thì W2 = Z2 (Wald test giống với kiểm định Z trên cơ sở βP là hệ số hồi quy ước lượng trung bình và, SE của βP chính là độ lệch chuẩn). Chúng ta có thể dựa trên kết quả tra bảng và kết quả kiểm định, nếu kết quả kiểm định > kết quả tra bảng, ngoài ra cũng dựa vào p-value để xét. Nếu xét trên giá trị p-value, bác bỏ H0 khi p-value < α. (p-value là mức ý nghĩa nhỏ nhất mà tại đó H0 bị bác bỏ).
Likelihood ratio test
Sau khi chúng ta tìm được các hệ số hồi quy cho các biến độc lập x sử dụng các phần mềm thống kê và thông qua phương pháp Maximum Likelihood Estimation trên cơ sở những hệ số hồi quy tìm được sẽ tối đa khả năng biến mục tiêu y đạt được 1 giá trị cụ thể trong tập giá trị của nó, hay các sự kiện mong đợi xảy ra.
Sau khi tìm được hệ số hồi quy, cũng như trước mắt chúng ta đã xác định được các biến độc lập x nào cần đưa vào mô hình từ phương trình hồi quy. Trong hồi quy tuyến tính, chúng ta có các chỉ tiêu đo lường độ hiệu quả như SST (Total Sum Of Squares), SSR (Sum of Squares due to Regression), SSE (Sum of Squares due to Errors) dùng để ước lượng sai số giữa giá trị thực tế và giá trị dự báo hay còn gọi là một phần của Residual Analysis, kiểm định t và kiểm định F cùng với R2 (hệ số xác định) để đánh giá liệu một biến hay nhiều biến có mối quan hệ với biến mục tiêu hay không, có ý nghĩa để thêm vô mô hình không?
Trong đó R2 – Coefficient of Determination được dùng phổ biến để so sánh các mô hình hồi quy tuyến tính với nhau ví dụ điển hình giữa 2 mô hình bao gồm một mô hình không có biến độc lập cần xét và một mô hình có biến độc lập cần xét, nếu R2 mô hình 2 cao hơn chứng tỏ biến độc lập này có ý nghĩa thêm vào mô hình vì nó làm tăng R2. Hệ số xác định R2 thể hiền phần tỷ lệ biến thiên của y mà chúng ta có thể giải thích bởi mối quan hệ tuyến tính giữa x và y.
Giống với hướng tiếp cận của R2, trong hồi quy logistic chúng ta có phương pháp Likelihood Ratio Test (LR), một dạng kiểm định dựa trên so sánh 2 mô hình để xác định một hay các biến độc lập x có phù hợp đưa vào phân tích hay không, gồm một mô hình từ phương trình hồi quy tìm được có các biến được chọn lọc, và mô hình còn lại đầy đủ, nói cách khác là một mô hình sẽ là “tập con” của mô hình còn lại. Lưu ý, mặc dù khác nhau về cách thức, nhưng giữa hồi quy logistic, và các dạng phân tích hồi quy khác đều tuân theo chung 1 quy tắc khi đánh giá độ hiệu quả của mô hình chính là: xem xét kết quả thực tế của biến mục tiêu và kết quả dự báo cho biến mục tiêu có được từ mô hình.
LR còn có thể đánh giá toàn bộ mô hình bao gồm tất cả các biến độc lập x hoặc chỉ đánh giá một biến độc lập x mà thôi. Với đánh giá 1 biến độc lập có ý nghĩa phân tích hay không, LR sẽ hướng đến so sánh giữa một mô hình không chứa biến đó và một mô hình chứa biến đó.
Chúng ta sẽ so sánh cái gì? Trong hồi quy tuyến tính, chúng ta có thể so sánh R2 giữa 2 mô hình, R2 ở mô hình nào cao hơn thì mô hình đó được chọn tức biến độc lập đang xét nếu có trong mô hình được chọn thì nghĩa là phù hợp để đưa vào phương trinh, còn nếu không có thì nghĩa là không có ý nghĩa phân tích. Đối vơi hồi quy logistic, chúng ta sẽ dựa vào Likelihood Function mà chúng tôi đã giới thiệu ở bài viết trước, tức là so sánh dựa trên xác suất thể hiện khả năng biến mục tiêu y nhận một giá trị cụ thể, mô hình nào giá trị likelihood cao hơn sẽ được chọn. Hướng tiếp cận khác là sự khác biệt giữa likelihood của 2 mô hình sẽ được kiểm định bằng cách lấy kết quả tỷ lệ, nếu sự khác biệt có ý nghĩa, thì mô hình có chứa biến cần xét là thích hợp để sử dụng. Nói có vẻ khó hiểu, chúng ta cùng đi qua chi tiết phương pháp.
Trường hợp chúng ta đang xét một biến thì Likelihood ratio có công thức như sau:
![]()
Với L0 là likelihood của mô hình không chứa biến cần xét với hệ số hồi quy của biến đó bằng 0, L1 là likelihood của mô hình chứa biến cần xét với H0: mô hình L0 phù hợp
Trường hợp chúng ta có trên 2 biến độc lập đang xét, chúng ta sẽ so sánh mô hình một là mô hình không có 2 biến đó gọi là mô hình con (subset), với mô hình 2 là mô hình đầy đủ có chứa 2 biến đó (full). Với giả thuyết H0 mô hình subset là phù hợp.
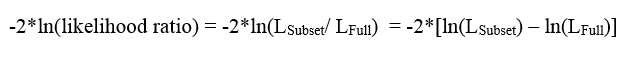
Trường hợp chúng ta đánh giá tổng thể mô hình hiện tại bao gồm các biến độc lập và hệ số hồi quy xác định được từ phương trình tìm được (có thể gọi là reduced/ fitted/ current model). Chúng ta sẽ so sánh với mô hình “đầy đủ nhất” tức mô hình này sẽ bao gồm tất cả các biến độc lập và tất cả mối quan hệ giữa các biến độc lập với tất cả hệ số hồi quy tương ứng gọi là Saturated model, trong mô hình này giá trị dự báo sẽ tiến gần bằng giá trị thực tế.
![]()
Đối với trường hợp cuối cùng, thì kết quả đạt được còn gọi là Deviance ký hiệu là D gọi là sai lệch giữa mô hình tìm được so với thực tế. Như vậy công thức tổng quát chưa chuyển hàm log

Ngoài việc cách đánh giá ý nghĩa của một biến theo trường hợp 1, chúng ta có thể sử dụng Saturated model hay Deviance để xem xét có nên đưa vào hay loại bỏ một biến độc lập bất kỳ khỏi mô hình:
![]()
Chúng tôi gọi mô hình không chứa biến cần xét là m0 thì D (m0) = -2*[ln(Lm0) – ln(Lsaturated)], xét tương tự cho mô hình chứa biến cần xét.
D trong hồi quy logistic đóng vai trò giống như Residual Sum of Squares hay còn gọi là SSE – Sum of squares trong hồi quy tuyến tính, còn G trong hồi quy logistic giống như kiểm định F từng phần trong hồi quy tuyến tính.
Lưu ý: Likelihood ratio được giả định xấp xỉ phân phối chi bình phương χ2 (Chi-squared distribution), -2 ở đầu công thức được đưa vào để điều chỉnh quy luật phân phối xấp xỉ theo phân phối chi bình phương.
Như vậy các kết quả đạt được từ những trường hợp trên chúng ta có thể ra bảng phân phối chi bình phương hoặc tìm ra p – value sử dụng phần mềm thống kê để kết luận bác bỏ hay không bác bỏ các giả thuyết H0 và kết luận mô hình nào phù hợp hay biến đã xét có thích hợp đưa vô mô hình không. Bậc tự do (degrees of freedom) chính là số chênh lệch trong tổng số biến độc lập của 2 mô hình. Lưu ý các trường hợp khác nhau, giả thuyết đặt ra sẽ có thể khác nhau, nên tránh nhầm lẫn giữa đặt giả thuyết và đưa ra các kết luận. Cụ thể như thế nào bài viết sắp tới về ứng dụng chúng tôi sẽ giải thích kỹ hơn.
Lưu ý kết quả Log likelihood các bạn có thể tìm thấy khi sử dụng các phần mềm phân tích mà không phải tự tính tay, vì nó rất phức tạp. Cũng vì thế mà ít có tài liệu về hồi quy logistic đề cập về công thức tổng quát của LR xét theo hàm likelihood. Chúng tôi có tham khảo thêm một số tài liệu, thì có một tài liệu quốc tế đề cập về phương trình tổng quát này, là tài liệu Applied Logistic Regression của tác giả David W. Hosmer, Stanley Lemeshow Rodney và X. Sturdivant
Công thức tổng quát của Deviance và ∆D = G được tham khảo:
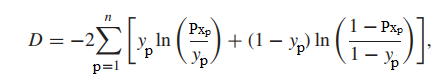
Trong đó Pxp là xác suất Yp = 1 hay Yp = 0 tại xp, n là tổng số quan sát trong tập dữ liệu, X1, X2,…Xp là các quan sát trong tập dữ liệu.
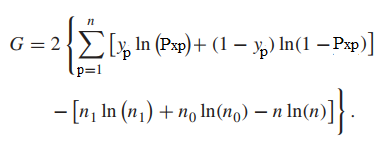
Bậc tự do của G trong kiểm định chi bình phương là bằng 1, ví số biến chênh lệch giữa 2 mô hình là bằng 1. Lưu ý mặc dù áp dụng các trường hợp khác nhau nhưng kết quả thu được có thể sẽ giống nhau ví dụ kết quả trường hợp 2 có thể bằng G trong kết quả trường hợp 3.
Score test
Phương pháp kiểm định để xác định ý nghĩa của một biến độc lập x có thích hợp đưa vào phân tích hay không mà không cần phải ước lượng hay tính toán ban đầu hệ số hồi quy. Công thức Score test và quy luật phân phối của nó đều dựa trên kết quả đạo hàm của hàm log likelihood mà cụ thể thì chúng tôi xin phép không đi vào quá chi tiết ở bài viết này vì nó khá phức tạp, ở đây chúng tôi chỉ giới thiệu sơ đến các bạn về Score test các bạn có thể tìm hiểu thêm ở các tài liệu khác. Công thức tổng quát đơn giản của Score test:
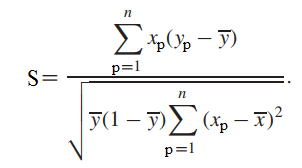
Với xp là giá trị của biến cần xét tại quan sát thứ p, Yp = 0 hay = 1 tại quan sát thứ p, ytb = số quan sát có y = 0 (hay y = 1) trên tổng số quan sát trong tập dữ liệu, xtb là giá trị trung bình của biến đang xét.
Score test cho phép chúng ta thêm các biến vào một mô hình có sẵn để xem các biến này có phù hợp hay không mà không cần xây dựng một phương trình tổng quát khác có chứa những biến mới và cả những biến cũ, không phải xây dựng 2 mô hình subset và full như trường hợp 2 ở likelihood ratio test. Ví dụ các bạn đã tìm ra một phương trình tổng quát hay mô hình ban đầu gồm có 2 biến x1 và x2, tìm được từ kết quả của các phần mềm thống kê tuy nhiên bạn quan tâm đến biến x3 và x4 cho rằng chúng có tác động nào đó lên kết quả dự báo của biến mục tiêu y, lúc này score test hay Lagrange test (tên gọi khác của score test) là cần thiết để áp dụng.
Các bạn có thể tìm thấy giá trị score test tại cột score test hay cột Lagrange test cho mỗi biến trong bảng kết quả thu được ở các phần mềm phân tích, xem xét giá trị p-value để kết luận giả thuyết. Score test hướng đến xem xét liệu độ phù hợp của mô hình trong dự báo có cải thiện gì khi thêm các biến mới vào. Lưu ý, Score test có quy luật phân phối giả định là phân phối chi bình phương χ2.
Nhận xét về Wald test, LR test, và Score Test
Thứ nhất về độ phức tạp trong tính toán thì LR là phức tạp nhất vì nó yêu cầu tính toán likelihood của cả 2 mô hình rồi mới lấy tỷ lệ, còn Wald test và Score test chỉ sử dụng một mô hình để xét. Thực tế khi tìm ra giá trị kiểm định từ 3 phương pháp trên cơ sở cùng xấp xỉ phân phối chi bình phương thì chúng thường không chênh lệch nhau quá nhiều, cụ thể thì bài viết tới về ứng dụng logistic regression chúng tôi sẽ trình bày các kết quả với ví dụ cụ thể. Mối quan hệ tiếp theo chính là mặc dù kết quả kiểm định có thể khác biệt nhưng kết luận sau cùng về mô hình và về biến độc lập là giống nhau. Với cỡ mẫu hay tổng số quan sát trong mẫu từ nhỏ đến trung bình, thì phương pháp kiểm định LR được ưu tiên hơn Wald test vì nhiều chuyên gia cho rằng LR đem lại kết quả chính xác hơn. Wald test và LR thường có sự bất đồng trong kết quả sau cùng ví dụ thông qua Wald test chúng ta bác bỏ giả thuyết H0 kết luận biến x nào đó không có ý nghĩa phân tích, nhưng kết quả LR thì ngược lại, cho rằng biến x đó có ý nghĩa phân tích. Đối với score test, thì khuyết điểm lớn nhất của nó chính là ít xuất hiện trong các phần mềm thống kê phổ biến. Câu hỏi đặt ra lựa chọn phương pháp kiểm định nào là hiệu quả? Theo thông lệ và cũng dựa trên nhiều nghiên cứu của các chuyên gia phân tích thì LR được chọn lựa vì công thức tính chặt chẽ, sử dụng likelihood function, bao quát xác định tính hiệu quả cả mô hình và cho ta thấy được tác động của các biến không phải chỉ 1 lên mô hình nếu được thêm vào hay bỏ ra. Thế nhưng liệu chúng ta có loại bỏ không sử dụng đến Wald test, hay Score test? Tốt nhất là không nên vì ở nhiều trường hợp vẫn có thể áp dụng 2 phương pháp này, thời gian và chi phí tính toán sẽ được giảm bớt do không quá phức tạp, đặc biệt nếu chúng ta muốn xác định nhanh ý nghĩa của các biến độc lập. Hơn nữa ngày nay chi phí tính toán không còn được coi trọng bởi sự xuất hiện của nhiều công cụ, phần mềm phân tích cạnh tranh, chúng ta cần quan tâm nhiều hơn vào độ hiệu quả sau cùng của mô hình nên việc xem xét và áp dụng nhiều phương pháp đánh giá khác nhau là cần thiết.
Ước lượng khoảng tin cậy cho hệ số hồi quy
Nếu các bạn nào đã theo dõi bài viết trước của chúng tôi về hồi quy tuyến tính cũng đã biết được lý do tại sao chúng ta thường quan tâm đến kết quả ước lượng khoảng tin cậy của hệ số hồi quy. Chúng tôi tóm gọn lần nữa lý do tại sao chúng ta phải ước lượng hệ số hồi quy.
Phương trình tổng quát mà chúng ta tìm được chỉ phản ánh mối quan hệ giữa các biến độc lập và biến mục tiêu trong phạm vi tập dữ liệu mẫu mà thôi ví dụ chúng ta biêt được tác động của số tiền khách hàng bỏ ra mua hàng ở năm ngoái lên khả năng đăng ký chương trình ưu đãi nhưng chỉ mới phân tích 100 khách hàng mà thôi, còn quá thiếu cơ sở để kết luận cho tổng thể hơn nữa, các hệ số hồi quy đều được ước lượng bằng MLE, chỉ mới là ước lượng điểm nên chắc chắn sẽ có sai số. Vậy cần thu thập và phân tích bao nhiêu thì mới đủ? Không thể biết được con số bao nhiêu là thực sự hợp lý. Nhưng trong lĩnh vực thống kê luôn có những phương pháp cho phép chúng ta suy luận với một mức độ chính xác nhất định về các giả định cho tổng thể nghiên cứu.
Như vậy để biết một cách tương đối trong thực tế tác động của từng biến độc lập lên xác suất để biến mục tiêu nhận một giá trị cụ thể trong hồi quy logistic chúng ta phải ước lượng khoảng tin cậy cho hệ số hồi quy.
Công thức ước lượng hệ số hồi quy trong logistic regression cũng tương tự như trong hồi quy tuyến tính, dựa trên kiểm định t hoặc Wald test, sử dụng sai số chuẩn tìm được của hệ số hồi quy:
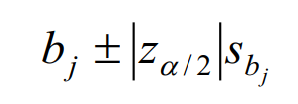
Với giá trị Sb chúng ta lấy từ kết quả của các phần mềm phân tích, tra bảng phân phối z để tìm giá trị za/2 với α là mức ý nghĩa.
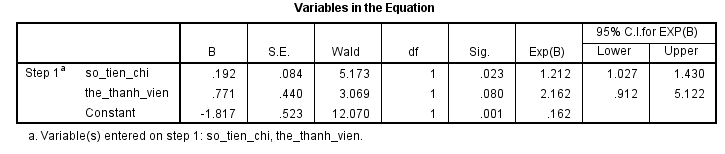
Chúng ta tính thử cho biến số tiền chi, mức ý nghĩa là 0.05, tra bảng z tìm được za/2 = 1.96
b1 ± 1.96* 0.084 = 0.164
β1 sẽ nằm trong khoảng (0.192 – 0.165; 0.192 + 0.165) = (0.027, 0.357)
Exp(β) là ước lượng của odds ratio mà chúng tôi trình bày ở phần 3, nhớ rằng:
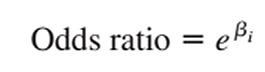
Chúng ta lấy log (1.027) thì thấy = 0.027, log(1.43) = 0.357, giống kết quả trên. Như vậy có thể kết luận phương pháp ước lượng cho odds ratio có thể áp dụng để ước lượng hệ số hồi quy.
Goodness of Fit
Khi xây dựng mô hình hồi quy logistic điều mà chúng ta quan tâm dĩ nhiên không phải chỉ có mỗi ý nghĩa của các biến độc lập có phù hợp hay có ý nghĩa phân tích để đưa vô mô hình phục vụ dự báo cho biến mục tiêu hay không đó chính là khả năng dự báo chính xác kết quả đạt được của biến mục tiêu so với thực tế. Vì ứng dụng sau cùng của hồi quy logistic là phân tích dự báo (predictive analytics) hay phân loại đối tượng dữ liệu (classification task).
Goodness of fit – dịch từ tiếng Việt dễ hiểu nhất là mức độ phù hợp. Mô hình chúng ta xây dựng thực chất mới chỉ khớp với hay mang đặc trưng của bộ dữ liệu mẫu hoặc có thể là dữ liệu training (chưa xét đến validation data) nên nó sẽ đưa ra kết quả dự báo tỷ lệ chính xác với những đối tượng nghiên cứu trong tập dữ liệu này, còn các đối tượng trong dữ liệu thực tế hay dữ liệu test thì sao? Độ phù hợp của mô hình để dự báo kết quả trong thực tế là như thế nào chính là nhiệm vụ của các phương pháp Goodness of fit. Quyết định sau cùng để một mô hình hồi quy logistic có thể được đưa vào ứng dụng trong các quy trình vận hành ở những lĩnh vực, ngành nghề chính là nằm ở khâu cùng cuối – thực hiện đánh giá Goodness of fit.
Discrimination & Validation
Discrimination là phương pháp đánh giá khả năng mô hình phân loại đúng 2 giá trị định tính cho đối tượng dữ liệu, dễ hiểu hơn ví dụ để đánh giá khả năng mô hình phân loại chính xác khách hàng tín dụng có khả năng “nợ xấu” và “không nợ xấu” thì chúng ta phải dùng phương pháp Discrimination. Discrimination là một trong những kỹ thuật đánh giá độ hiệu quả của những mô hình làm nhiệm vụ phân loại đối tượng dữ liệu hay còn gọi là Classification task. Điển hình trong Discrimination áp dụng cho hồi quy logistic chúng ta có phương pháp Confusion Matrix gồm những chỉ số True Positive (TP), False Positive (FP), False Negative (FN), True Negative (TN) áp dụng để tính ví dụ Precision (Positive Predicted Value), Accuracy rate, Sensitivity và Specificity,.. cơ sở để xây dựng đồ thị ROC (Receiver operating characteristic) và xác định AUC (area under the curve).
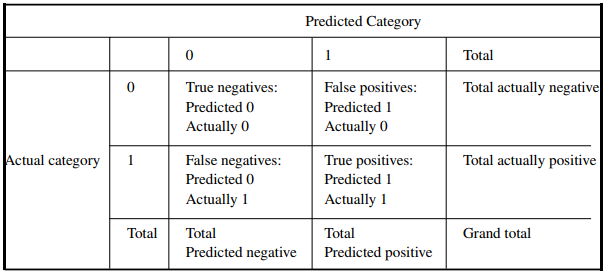
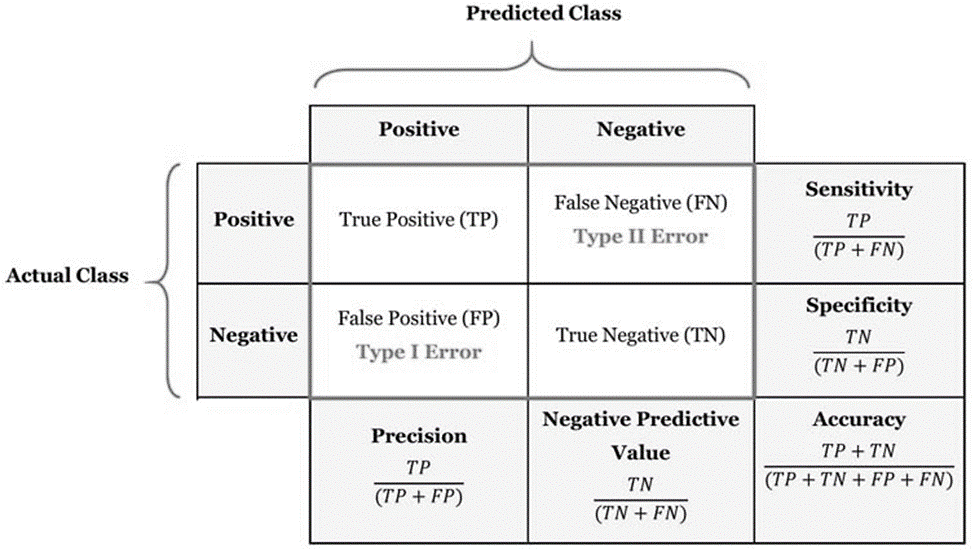
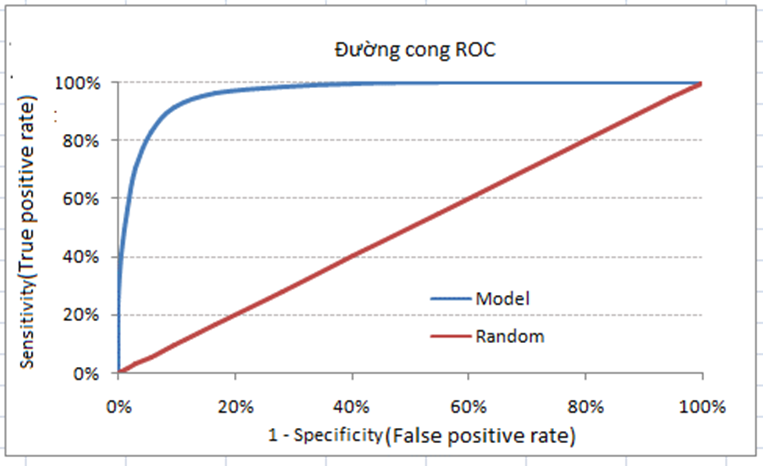
Còn về validation đơn giản là phương pháp đánh giá độ hiệu quả của mô hình trong việc dự báo hay phân loại đối tượng dữ liệu trên nhiều tập data khác nhau. Nếu những bạn nào đã làm quen lĩnh vực phân tích dữ liệu thì chắc hẳn đã quá quen thuộc với quy trình đầu tiên sau khi thu thập, làm sạch, chuẩn bị dữ liệu đó chính là chia tập dữ liệu thành dữ liệu training (có thể có dữ liệu validation) và dữ liệu test với tỷ lệ cụ thể nào đó có thể dựa trên kinh nghiệm phân tích. Sau đó xây dựng mô hình trên dữ liệu training và thử nghiệm mô hình trên dữ liệu test, đảm bảo mô hình dự báo kết quả sát với thực tế – lấy kết quả thử nghiệm trên dữ liệu test để đánh giá. Đó chỉ là một ví dụ về các phương pháp trong Validation.
Về các phương pháp đánh giá mô hình phân loại cũng như Discrimination & Validation chúng tôi có một bài viết trình bày cụ thể nên các bạn có thể tham khảo theo link dưới đây:
Phương pháp đánh giá mô hình phân loại (Classification model evalutation)
Bên cạnh Discrimination và Validation chúng ta còn có các phương pháp áp dụng đánh giá tổng quát độ chính xác của hồi quy logistic trong việc dự báo.
Calibration
Calibration dịch sang tiếng Việt có nghĩa là căn chỉnh, và hiệu chuẩn,… tuy nhiên vẫn chưa có một thuật ngữ tiếng việt chính xác có thể mô tả rõ và khái quát mục đích của phương pháp này, nên chúng tôi vẫn sẽ để tiếng Anh. Calibration là phương pháp đánh giá cũng như gia tăng khả năng (xác suất) mô hình đưa ra các dự báo phân loại đối tượng nghiên cứu là “positive” gần giống với tỷ lệ trong thực tế của các “positive”– với positive kết quả hướng đến có tính tích cực, và được quan tâm nhiều hơn. Nói cách khác chúng ta dùng calibration khi chúng ta quan tâm kết quả phân loại của một đối tượng nghiên cứu đặc biệt ví dụ quan tâm khả năng khách hàng rời dịch vụ hơn không rời dịch vụ, khả năng khách hàng nợ xấu hơn không nợ xấu.
Calibration hướng đến cải thiện mô hình sao cho xác suất từ kết quả dự báo sẽ bằng tỷ lệ trong tập dữ liệu training (dữ liệu thực tế thu thập trước khi phân tích)
Giả sử chúng ta có tập dữ liệu mẫu lịch sử gồm 100 khách hàng thân thiết trong đó có 80 khách hàng đăng ký ưu đãi, 20 khách hàng không đăng ký ưu đãi. Chúng ta quan tâm đến khách hàng đăng ký ưu đãi để đánh giá chiến lược marketing, dịch vụ CSKH có hiệu quả hay không. Như vậy tỷ lệ positive thực tế là 0.8, negative là 0.2. Sau đó chúng ta xây dựng mô hình, tinh chỉnh, chọn lọc các biến, làm các cách để sao cho xác suất trung bình dự báo khả năng khách hàng đăng ký ưu đãi sẽ gần bằng 0.8. Nếu làm được điều này tức mô hình đã được “calibrated tốt”.
- Hosmer–Lemeshow
Có nhiều phương pháp đánh giá và cải thiện Calibration của một model logistic regression mà phổ biến nhất là kiểm định Hosmer–Lemeshow. Giả sử có một tập dữ liệu gồm N quan sát, chúng ta chia tập dữ liệu này thành M số các tập con có cùng số quan sát. Chúng ta sẽ sắp xếp các tập con theo thứ tự tăng dần của xác suất trung bình dự báo ví dụ tập đầu tiên có xác suất dự báo khả năng khách hàng đăng ký ưu đãi trung bình là 0.1, tập thứ 2 sẽ hơn 0.1 cho đến tập thứ k tập này sẽ có xác suất cao nhất (nhưng không chắc bằng 1 tuyệt đối). Nhiệm vụ là chúng ta phải so sánh ở từng tập con tỷ lệ positive thực tế so với xác suất trung bình được dự báo là như thế nào. Nếu không có sự chênh lệch nhiều thì chứng tỏ mô hình đã được calibrate tốt hoặc ngược lại. Công thức kiểm định của Hosmer-lemeshow dựa trên giả định xấp xỉ phân phối chi bình phương sẽ cho chúng ta thấy có sự khác biệt tổng quát giữa xác suất trung bình dự báo và tỷ lệ thực tế hay không trong các tập con và cả tập dữ liệu, sự khác biệt này có ý nghĩa hay không?
Công thức kiểm định Chi-bình phương:
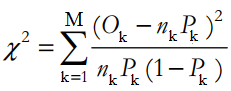
Với M là tổng số tập con, k là thứ tự tập con, Ok là số quan sát là positive trong tập thứ k, nk là tổng số quan sát trong tập thứ k, Pk là xác suất dự báo positive trung bình trong tập k. Chúng ta sẽ tra bảng với mức ý nghĩa α, và bậc tự do là M – 2 với M là số tập con.
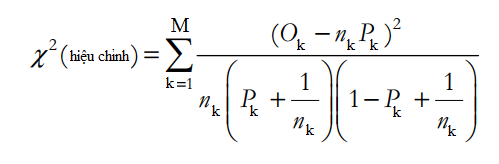
Bên trên là công thức hiệu chỉnh trong trường hợp P quá lớn hay quá bé tức tiến gần 0 hoặc 1, khiến cho kết quả thu được không hợp lý.
Giả thuyết Ho trong phương pháp này đó chính là các giá trị dự báo expected sẽ gần bằng các giá trị quan sát thực tế observed. Do đó nếu p-value tính được càng nhỏ thì khả năng bác bỏ Ho càng cao tức mô hình không có độ chính xác trong dự báo.
Hình bên dưới là đồ thị đánh giá Calibration của một mô hình trục tung là tỷ lệ positive kỳ vọng, chính là xác suất trung bình dự báo từ phương trình hồi quy tìm được, trục hoành là tỷ lệ quan sát thực tế. Các điểm dữ liệu nào nằm trên được thẳng màu đỏ cho thấy sự bằng nhau giữa 2 giá trị, càng nhiều điểm nằm gần đường này hay nằm trên sẽ cho thấy mô hình logistic regression đang hiệu quả.
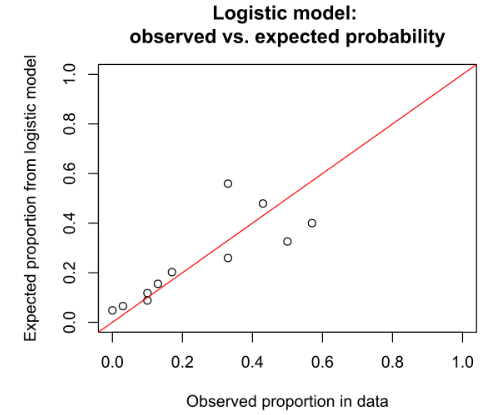
(nguồn hình enwikipedia)
Vẫn còn 2 phương pháp quan trọng khác là kiểm định chi bình phương và các công thức xác định R2 chúng tôi sẽ trình bày tóm gọn ở phần sắp tới trước khi đi vào ví dụ ứng dụng cụ thể do bài viết hiện tại đã quá nhiều nội dung có thể khiến các bạn cảm thấy ngán.
Mong các bạn sẽ tiếp tục ủng hộ BigDataUni.
Tài liệu tham khảo:
- Applied Logistic Regrssion của tác giả David W. Hosmer, Stanley Lemeshow Rodney và X. Sturdivant;
- Model performance analysis and model validation in logistic regression của tác giả R. Arboretti Giancristofaro, L. Salmaso,
- Measures of Fit for Logistic Regression của tác giả Paul D. Allison.
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English