Trải qua 4 phần bài viết trong chủ đề clustering, BigDataUni và các bạn đã cùng nhau tìm hiểu sơ lược về thuật toán clustering, về các dạng phổ biến trong clustering như Hierarchical và K-means với ví dụ cụ thể, chúng ta cũng đã đi qua hai phần bài viết giới thiệu về mô hình RFM kết hợp K-means clustering trong phân khúc khách hàng hỗ trợ các hoạt động sales, marketing hiệu quả.
Link các bài viết trước cho các bạn tham khảo:
Link các bài viết dành cho những bạn chưa tham khảo các bài viết trước
Tìm hiểu về phương pháp Clustering (phân cụm) (P.1)
Tìm hiểu về phương pháp Clustering (P.2): Hierarchical clustering đơn giản
K-means Clustering và mô hình RFM (P.1)
K-means clustering và mô hình RFM (P.2)
Đến với bài viết cuối của series đầu tiên về clustering, chúng ta sẽ tìm hiểu về các phương pháp cơ bản đánh giá những cluster tìm được trước khi triển khai áp dụng vào thực tế. Cũng giống như các thuật toán trong Classification, hay bất kỳ thuật toán nào khác trong Data mining, Clustering cũng cần có các cơ sở để kết luận độ phù hợp, độ chính xác.
Ở bài viết K-means clustering và RFM chúng tôi đã nhắc đến bước đầu tiên khi triển khai thuật toán chúng ta phải xác định số k, số các cụm muốn phân từ tập dữ liệu.
Tuy nhiên quyết định bao nhiêu cụm cần phân như thế nào để tối ưu nhất và các cụm có được khi kết thúc thuật toán clustering được đánh giá là phù hợp, chính xác, đáng tin cậy thì cực kỳ quan trọng và cần có phương pháp cụ thể. Nếu quá trình chọn k được thực hiện chỉ dựa trên kinh nghiệm phân tích, kiến thức chuyên môn, và mục đích kinh doanh mà không dựa trên chính đặc tính của dữ liệu thì khả năng cao việc ứng dụng clustering sẽ không mang lại giá trị như mong đợi khi các cluster có thể không phản ánh tốt các quy luật, các mối quan hệ những đối tượng quan sát trong tự nhiên đang tiềm ẩn trong tập dữ liệu.
Elbow method
Xác định số k cluster trước khi xây dựng thuật toán K-means clustering như đã nói ở trên là cực kỳ quan trọng không chỉ vì k-means clustering cần tham số k ban đầu để vận hành thuật toán mà còn số k để kiểm soát quá trình phân cụm, và phân tích các cụm sao cho tối ưu, nói đơn giản là tiết kiệm thời gian xác định trong thực tế có bao nhiêu cụm là phù hợp.
Nói đến cách chọn số k hiệu quả thì thực chất rất nhiều, nó kết hợp không chỉ dựa trên những phương pháp mà còn kinh nghiệm của chuyên gia phân tích.
Elbow method là phương pháp xác định số k cho k-means clustering được coi là phổ biến nhất, bên cạnh các phương pháp khác như Pseudo F-statistic hay Silhouette index mà chúng tôi sắp trình bày dưới đây.
Elbow method được minh họa dưới dạng đồ thị đường cong với trục hoành là số k các cluster, trục tung sẽ là tiêu chí đánh giá bao gồm SSE, Silhouette. Ở phần này chúng ta tìm hiểu trước về SSE – Sum of Errors – đo lường sự khác biệt giữa các điểm trong cluster. Trong k-means clustering, SSE được tính là tổng các khoảng cách tính từ các điểm trong cluster đến điểm trung tâm Centroid của cluster, tính tất cả các cluster, dựa theo công thức Euclidean. Khi các điểm dữ liệu hay các object, các quan sát càng gần nhau thì sẽ có đặc điểm gần giống nhau, được phân trong một cụm, thì cụm đó chứng tỏ “chất lượng” và ngược lại.
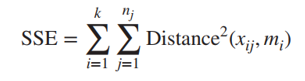
Sẽ có k cluster cần tính giá trị SSE thường k sẽ chạy từ 1 đến 10 hay 20. Như vậy với mỗi k chúng ta sẽ có 1 SSE. Minh họa các cặp k và SSE lên đồ thị. Số k tối ưu chính là điểm mà ở đó SSE bắt đầu giảm đều, nhìn trên đồ thị nó là điểm “turning point”, nói vui điểm nằm ở vị trí “cùi chỏ” sẽ là số k cần tìm.
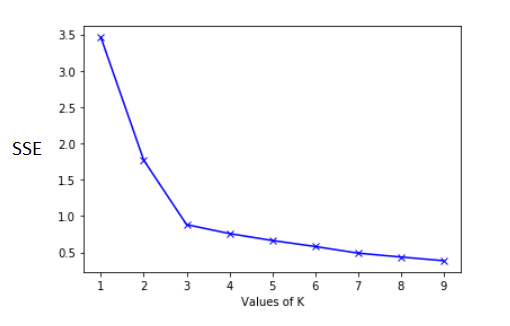
Nhìn hình minh họa giống khuỷu tay, k = 3 sẽ thích hợp là số cụm ban đầu cần phân của k-means clustering.
Giải thích: Elbow method dựa trên giả định khi càng có nhiều cluster, thì có nghĩa các điểm dữ liệu giống nhau đã được gom cụm, mỗi cụm sẽ chỉ có ít điểm dữ liệu bên trong, và những điểm này sẽ ko nằm xa nhau, do đó SSE sẽ giảm, khi k tăng. Tuy nhiên khi k càng tăng chúng ta sẽ càng có nhiều cluster cần phân tích, dẫn đến không hiệu quả. Do đó chúng ta nên chon số k mà ở đó SSE bắt đầu giảm đều. Đây được xem là quy tắc chung khi sử dụng elbow method.
SSE chỉ đánh giá tính cohesion của mỗi cluster, chúng tôi sẽ nói đến cohesion. Silhouette được ưu tiên hơn SSE vì nó đánh giá cả Separation. Chúng tôi sẽ giải thích chi tiết 2 đặc tính đánh giá độ phù hợp của kết quả phân cụm ở phần sau bài viết.
Kiểm định Hopkins
Để xác định xem tập dữ liệu có các cụm hay không chính là cố gắng phân cụm nó. Tuy nhiên, hầu như tất cả các thuật toán phân cụm sẽ tìm các cụm một cách cẩn thận khi được cung cấp dữ liệu. Chúng ta có thể đánh giá kết quả phân cụm và kết luận rằng trong tập dữ liệu có các cluster nếu ít nhất một số cluster có chất lượng tốt. Tuy nhiên, cách tiếp cận này không giải quyết được thực tế là các cụm trong dữ liệu có thể đã được xác định từ trước đó, khác với các cụm được tìm kiếm bởi thuật toán clustering. Nói đơn giản, dữ liệu đã được phân cụm và chúng ta đang cố gắng sử dụng thuật toán clustering để tìm ra chúng, tuy nhiên kết quả của chúng ta có thể khác với các cụm đã có trong tập dữ liệu.
Kiểm định Hopkins giúp ta đánh giá liệu có hay không có các cluster trong dữ liệu mà chúng ta có thể tìm thấy khi không cần dùng đến các thuật toán như k-means clustering. Hướng tiếp cận của phương pháp Hopkins là đánh giá sự phân bố đồng đều của dữ liệu. Nếu dữ liệu được phân bố đồng đều (dữ liệu có thể đã có clusters) thì tức các cluster tìm được qua các thuật toán clustering có thể không có ý nghĩa hoặc ngược lại. Việc đánh giá này còn được gọi là tìm hiểu Cluster tendency
Giả sử chúng ta có một tập dữ liệu A. Lấy mẫu trong tập dữ liệu gốc A, với mỗi điểm pi mẫu, tìm điểm pj trong tập A gần nhất với nó và tính khoảng cách, wi = dist(pi, pj)
Chúng ta tạo một tập dữ liệu ảo, với một số điểm dữ liệu được phân bố ngẫu nhiên trên không gian dữ liệu, Cho mỗi điểm pi trong tập dữ liệu ảo này, tìm điểm pj trong tập dữ liệu gốc A gần nhất với nó và tính khoảng cách, ui = dist(pi, pj)
Công thức Hopkins:
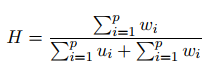
Nếu H = 0.5, tức khoảng cách giữa các điểm dữ liệu ảo đến các điểm láng giềng gần nhất trong tập dữ liệu A, sẽ bằng với khoảng cách ngắn nhất giữa các điểm dữ liệu gốc đến các điểm láng giềng gần nhất của chúng nằm trong tập dữ liệu A ban đầu. H tiến gần 0, hoặc 1, thể hiện dữ liệu gốc đã được sắp xếp, được phân cụm, không mang tính ngẫu nhiên, và chúng ta không cần triển khai clustering.
Các phương pháp đánh giá kết quả phân tích clustering
Từ thống kê cho đến Data mining, khai phá dữ liệu, từ các kết luận về tổng thể nghiên cứu, cho đến việc xây dựng các mô hình phân tích, tất cả đều phải được đánh giá một cách cụ thể, đây là bước quan trọng và yếu tố cốt lõi đóng góp vào khả năng thành công trong việc ứng dụng phân tích dữ liệu vào thực tế. Do đó, Clustering cũng không phải ngoại lệ.
Nói về các phương pháp đánh giá các phân cụm tìm được khi thực hiện những thuật toán clustering thì khó có thể kể hết, và có nhiều hướng tiếp cận khác nhau, phụ thuộc vào loại dữ liệu (định tính, định lượng), phụ thuộc vào loại clustering (ví dụ hierarchical hay k-means clustering), phụ thuộc vào thông tin có được (chính tập dữ liệu, dữ liệu bên ngoài),…
Đã có hàng loạt các chuyên gia nghiên cứu để tìm ra các phương pháp đánh giá tiêu chuẩn, đúng nhất, phù hợp nhất có thể áp dụng được cho mọi trường hợp triển khai clustering. Tuy nhiên hiện tại vẫn chưa khẳng định liệu có một cách thức chung, nhất quán, tốt nhất hay không.
Trong bài viết lần này, chúng ta sẽ tập trung vào các công thức đánh giá clustering phổ biến, được sử dụng rộng rãi, một cách đơn giản, và không mấy phức tạp, dễ hiểu giúp các bạn dễ nắm bắt.
Để có cái nhìn tổng quan về phương pháp đánh giá clustering chúng ta phải tìm hiểu chi tiết mục đích tại sao phải kiểm tra các clusters có được từ mô hình thuật toán phân cụm, ví dụ thông qua các câu hỏi sau:
- Các cluster tìm được có tương ứng hay đúng với thực tế hay đơn giản chỉ là giả thuyết, suy luận ở góc độ toán học?
- Chính xác thì sẽ có bao nhiêu cụm hay số cụm được phân tối ưu là bao nhiêu? Cái này thì chúng ta đã nói ở phần trên, elbow method.
- Giữa 2 kết quả phân cụm A và B, mỗi kết quả sẽ có cách phân cụm và số cụm khác nhau, thì kết quả nào sẽ phù hợp hơn để ứng dụng vào thực tế.
- Xác định khuynh hướng phân cụm (clustering tendency) tức là tìm hiểu xem cấu trúc của mỗi cụm tìm được có phi ngẫu nhiêu hay theo một quy tắc nào đó không?
- Đo lường chất lượng của mỗi phương pháp phân cụm áp dụng, thông qua kết quả phân tích có được, xác định: các clusters có “fit” với dữ liệu hay không (mô hình hoạt động tốt trên training data thì khi sử dụng testing data có vấn đề gì không), các cluster tìm được và trong thực tế có giống nhau không, các đối tượng thuộc các cluster tìm được trong thực tế có được phân loại đúng như vậy hay không (sử dụng dữ liệu classified trong thực tế nếu có để so sánh)
Cũng từ các câu hỏi trên mà những phương pháp đánh giá clusters được chia làm 2 loại chính:
- Unspervised (internal indices/ internal criteria/ internal information/ intrinsic method): các phương pháp đánh giá độ hiệu quả, sự phù hợp của các clusters mà không sử dụng các thông tin bên ngoài tập dữ liệu, chỉ sử dụng những thông tin có sẵn trong tập dữ liệu. Thường được chia làm 2 loại: các phương pháp đo lường tính liên kết trong cụm (cluster cohesion – độ gắn kết, chặt chẽ), xác định mức độ liên quan chặt chẽ của các đối tượng trong một cụm và các phương pháp phân đo lường tính tách biệt giữa các cụm cụm (cluster seperation – cô lập), xác định mức độ khác biệt hoặc tách biệt của một cụm so với các cụm khác.
Lưu ý, mỗi phương pháp clustering sẽ có cách đánh giá cohesion và seperation giữa các cluster là khác nhau. Ví dụ điển hình là phương pháp phân cụm dựa trên đồ thị hay còn gọi Graph-based clustering (ở series khác về clustering trong tương lai chúng tôi sẽ nói đến chi tiết hơn) với K-means clustering (Prototype-based clustering cho dữ liệu định lượng):
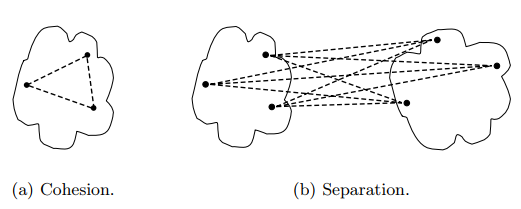
Phương pháp Graph-based clustering
(nguồn hình “Introduction to Data mining” – Pearson, tác giả Tan, Steinbach, Kumar)
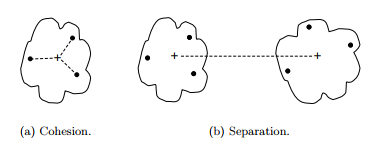
Phương pháp Prototype-based clustering (K-means clustering)
(nguồn hình “Introduction to Data mining” – Pearson, tác giả Tan, Steinbach, Kumar)
Graph-based: Nếu khoảng cách giữa các điểm nằm trong cluster càng nhỏ, tức các điểm không quá khác biệt nhau, variation trong cluster nhỏ, chứng tỏ cluster cohesion cao, kết quả phân cụm tốt và ngược lại. Còn cluster separation đo lường khoảng cách ngắn nhất giữa 2 điểm dữ liệu hay 2 đối tượng quan sát thuộc 2 cluster bất kỳ để xác định khoảng cách giữa 2 cluster, nếu khoảng cách này càng giảm thì độ khác biệt giữa 2 cluster càng thấp, kết quả phân cụm chưa được tối ưu và ngược lại.
Prototype-based: Nếu khoảng cách giữa các điểm dữ liệu đến Centroid càng nhỏ, chứng tỏ cluster cohesion cao kết quả phân cụm tốt và ngược lại. Còn cluster separation đo lường khoảng cách giữa 2 điểm Centroid, nếu khoảng cách càng xa, chứng tỏ sự khác biệt giữa 2 cluster cao, kết quả phân cụm tối ưu và ngược lại.
Trong bài viết này chúng ta tạm thời tập trung vào K-means clustering. Các bạn có thể thấy, tính toán cohesion ở K-means clustering sẽ dựa trên khoảng cách giữa từng quan sát trong cluster đến với điểm trung tâm (Centroid) còn seperation sẽ dựa vào khoảng cách giữa 2 Centroid của 2 cluster.
- Supervised (external indices/ external criteria/ external information/ extrinsic method): khác với unspervised, ở đây bên cạnh sử dụng dữ liệu mẫu có sẵn, chúng ta sẽ sử dụng thêm thông tin bên ngoài, cụ thể là dữ liệu về các đối tượng quan sát đã được phân loại sẵn (có mang “nhãn” nhận diện) nếu có để so sánh với kết quả phân cụm (mỗi cụm sẽ có tên gọi riêng). Các phương pháp đánh giá Supervised này có hướng tiếp cận gần giống với Classification. Mục đích là để tìm hiểu các cluster tìm được có gần giống số class đúng như thực tế hay không và cluster của mỗi quan sát có chính là class của quan sát đó hay không. Ví dụ cluster của khách hàng A là “Khách hàng trung thành”, xét trong tập dữ liệu thu thập và xử lý gần đây, khách hàng A đã được phân loại là khách hàng trung thành hay chưa. Với giả định, độ chính xác càng cao thì hiệu quả clustering sẽ tăng lên, phù hợp để ứng dụng trong thực tế. Tuy nhiên, sự thật rằng khi chúng ta lần đầu phải sử dụng đến thuật toán clustering cho một tập dữ liệu mới, thì thông tin về các class chắc chắn không có. Nhưng ở những lần tiếp theo, khi đã có thêm thông tin, sử dụng Supervised method sẽ giúp cải thiện mô hình clustering trong tương lai
Ngoài ra con có thêm 1 loại nữa là Relative, tức so sánh các kết quả khác nhau khi triển khai clustering, có thể bao gồm các phương pháp Unsupervised hay Supervised để làm tiêu chí so sánh.
Do bài viết có giới hạn nên chúng tôi không thể gửi đến các bạn tất cả các phương pháp đánh giá clustering, mà chỉ tập trung vào Internal method trước, chọn lọc, và giới thiệu sơ lược một số cái được phổ biến, sử dụng rộng rãi.
Chỉ số Silhouette Index
Chỉ số Silhouette Index có lẻ là chỉ số đánh giá các kết quả phân cụm phổ biến và được sử dụng nhiều nhất. Phân tích chỉ số Silhouette mục đích để đo lường mức độ tối ưu khi một quan sát, một điểm dữ liệu được phân vào các cluster bất kỳ. Cụ thể, phương pháp Silhouette, với tên nghĩa tiếng Việt “cái bóng”, sẽ cho chúng ta biết những điểm dữ liệu hay những quan sát nào nằm gọn bên trong cụm (tốt) hay nằm gần ngoài rìa cụm (không tốt) để đánh giá hiệu quả phân cụm.
Silhouette đo lường khoảng cách của một điểm dữ liệu trong cụm đến Centroid, điểm trung tâm của cụm, và khoảng cách của chính điểm đó đến điểm trung tâm của cụm gần nhất (hoặc đến các điểm trung tâm của các cụm còn lại, và chọn ra khoảng cách ngắn nhất). Đó là trường hợp đo lường cho K-means clustering.
Nếu các cluster được tìm không phải dựa trên clustering, thì Silhouette cũng sẽ đo lường theo cách tương tự nhưng thay vì tính khoảng cách giữa điểm đó với điểm trung tâm, thì chúng ta sẽ tính khoảng cách trung bình với tất cả các điểm còn lại trong cluster của điểm đó, và khoảng cách trung bình với tất cả các điểm còn lại của các cluster khác (lấy khoảng cách trung bình ngắn nhất)
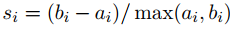
Giả sử có 2 cluster A và B được tìm thấy dựa trên K-means clustering
- bi là khoảng cách từ điểm i trong cluster A đến điểm trung tâm của cluster B
- ai là khoảng cách từ điểm i trong cluster A đến điểm trung tâm của cluster A
Nếu không phải K-means clustering thì:
- bi là khoảng cách trung bình từ điểm i trong cluster A đến tất cả các điểm trong cluster B với cluster B là cluster láng giềng gần nhất.
- ai là khoảng cách trung bình từ điểm i trong cluster A đến tất cả các điểm còn lại trong A
max(bi, ai) tức lấy chọn giá trị lớn nhất giữa ai và bi
Cách tính toán khá đơn giản, ví dụ như sau:

Giả sử có 5 điểm dữ liệu một chiều, được vẽ trên 1 đường thẳng, m1 là điểm trung tâm của cluster 1, m2 là điểm trung tâm của cluster 2, giả sử 5 điểm dữ liệu đều thuộc cluster 1. Cách tính như trên. Chúng ta có thể tính điểm trung bình để đánh giá tổng quan kết quả phân tích clustering, giá trị trung bình càng cao thì càng tốt, nhưng chỉ nằm trong khoảng -1 đến 1, với 1 là kết quả tốt nhất.
Giải thích: Silhouette là phương pháp tính toán kết hợp đánh giá cả Cohesion (qua ai) và Separation (bi). Nếu Silhouette tiến về -1, tức khoảng cách điểm i so với điểm trung tâm trong chính cụm nó được phân xa hơn so với điểm trung tâm của cụm còn lại, vậy khả năng điểm i lúc này bị phân sai cụm. Các bạn có thể xét ngược lại.
Do đó, bi – ai càng cao càng tốt, đạt max = bikhi ai = 0
Nếu một cluster được đánh giá chất lượng, là các điểm trong cluster sẽ có Silhouette tiến về 1 và ngược lại.
Để đánh giá nhanh liệu một điểm có được phân cụm đúng hay không chúng ta có thể dựa vào Silhouette:
- Điểm dữ liệu có Silhouette cao, gần bằng 1, chắc chắn nằm đúng trong cluster
- Điểm dữ liệu có Silhouette gần bằng 0, đang nằm giữa 2 cluster
- Điểm dữ liệu có Silhouette thấp, có giá trị âm thì khả năng đã nằm sai cluster.
Ngoài ra, theo kinh nghiệm của các tác giả trong tài liệu “Data mining and Predictive analytics” của nhà xuất bản Wiley:
- Điểm trung bình Silhouette từ 0.5 trở lên, bằng chứng cho thấy có thể cluster này sát với thực tế
- Điểm trung bình Silhouette từ 0.25 đến 0.5, thì cần thêm kiến thức chuyên môn, kinh nghiệm để đánh giá thêm khả năng cluster có trong thực tế
- Điểm trung bình dưới 0.25, thì không nên tin tưởng cluster, và cần đi tìm nhiều bằng chứng khác.
Pseudo F – statistic
Một phương pháp khác để đo lường độ chính xác của kết quả phân cụm xét trên tất cả các cluster đó chính là phương pháp kiểm định F. Phương pháp kiểm định F là phương pháp đánh giá quen thuộc trong phân tích hồi quy mà chúng ta đã từng làm quen. Vậy trong clustering kiểm định F được sử dụng như thế nào?
Giả sử chúng ta có số k các cluster, với ni là số các quan sát trong cluster i bất kỳ, vậy ∑ni = N là tổng quan sát có trong mẫu.
Tiếp theo, giả sử chúng ta có xij là giá trị của điểm j có trong cluster i, mi là điểm trung tâm của cluster i, và M là giá trị trung bình của tất cả điểm dữ liệu hay quan sát có trong tập dữ liệu
Chúng ta sẽ tính chênh lệch bình phương giữa các cluster, SSB (Sum of squares between clusters) đánh giá Separation
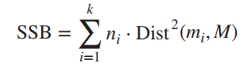
Sau đó chúng ta tính SSE, chênh lệch bình phương giữa các điểm bên trong cluster, đánh giá Cohesion
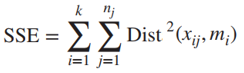
Công thức tính khoảng cách giống công thức Euclidean chúng tôi đã nhắc đến ở các bài viết trước:

Sau cùng giá trị kiểm định F như sau:
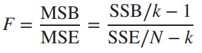
Chúng ta đặt giả thuyết như sau:
H0: Không có cluster trong tập dữ liệu
H1: Có số k cluster trong tập dữ liệu
Thông thường trong thực tế giá trị F tính được sẽ rất lớn, p-value sẽ rất nhỏ, và H0 thường bị bác bỏ ngay lập tức, do đó mà kiểm định F này còn có thêm chữ PSEUDO, nghĩa là “giả”, ở đầu. Nhiều người sẽ cho rằng phương pháp kiểm định F này là vô ích, khi chắc chắn trong tập dữ liệu sẽ luôn có các cluster, chúng ta cần gì kiểm định? Tuy nhiên, thực tế, dữ liệu ngày nay rất phức tạp, đa dạng làm sao chúng ta dám chắc sẽ có cluster, ví dụ chúng ta thu thập dữ liệu về thói quen ăn uống của 200 khách hàng đến từ 200 quốc gia khác nhau, có thể 200 khách hàng này khác nhau hoàn toàn thì sao?
Do đó kiểm định F trong một số trường hợp vẫn hữu ích để chúng ta đánh giá nhanh, nhưng điều quan tâm là có chính xác bao nhiêu cluster được phân trong tập dữ liệu. Kiểm định F sẽ giúp chúng ta tìm ra, cũng như đánh giá trong số các kết quả phân tích clustering tổng thể thì cái nào sẽ tốt nhất.
Cách làm đơn giản như phương pháp Elbow Method, chọn số k giống như ở trên:
Chúng ta sẽ chạy thử thuật toán với một loạt giá trị k – số clusters khác nhau, và ở mỗi giá trị k chúng ta sẽ tính F và tìm P-value. Số k nào có P-value bé nhất sẽ được chọn. Lưu ý ở đây chúng ta sẽ sử dụng P-value để làm tiêu chí chọn lựa sẽ chính xác hơn thay vì tìm F lớn nhất.
Chúng ta lấy lại ví dụ vừa rồi để tính thử để các bạn biết được cách triển khai công thức
Chúng ta có 5 điểm dữ liệu:
X1 = 0 đến X5 = 8, các điểm X1, X2, X3 giờ thuộc cluster 1, m1 = 3, X4, X5 thuộc cluster 2, m2 = 6. M trung bình = (0 + 2 + 4 + 6 +8)/5 = 4
SSB = SSBi = 1 + SSBi = 2 = 3*(3 – 4)2 + 2*(6 – 4)2 = 11
SSE = (0 – 3)2 + (2 – 3)2 + (4 – 3)2 + (6 – 6)2 + (8 – 6)2 = 15
N – k = 5 – 2 = 3; k – 1 = 2 – 1 = 1
Vậy F= 2.2. Chúng ta sẽ tra bảng F để tìm p-value với bậc tự do df1 = k – 1, df2 = N – k, hoặc sử dụng excel, hay các công cụ phân tích cung cấp giá trị sẵn. P-value ở đây bằng 0.065 > 0.05, nên ko bác bỏ H0, tập dữ liệu không có cluster.
Dunn’s Index
Chỉ số của Dunn, đây là phương pháp đánh giá cluster phổ biến khác sử dụng thông tin bên trong tập dữ liệu. Dunn’s Index đáng lẽ được đưa lên đầu tiên, bên trên Silhouette vì đây là phương pháp đơn giản nhất. Cách đánh giá dựa trên việc so sánh giữa kích thước (size) của các cluster với khoảng cách giữa các cluster với nhau. Các cụm càng xa nhau, so với kích thước của chúng, chỉ số càng lớn thì kết quả phân cụm sẽ càng chính xác.
Dunn’s Index, ký hiệu V(D) hay V(C) tính bằng cách lấy tỷ lệ giữa khoảng cách ngắn nhất giữa 2 cluster và kích thước lớn nhất của 2 cluster.

Cách tính như sau:
- Giả sử tính toán khoảng cách giữa 2 clusters k và k’, dựa trên tính toán khoảng cách giữa các điểm trong 2 cluster với nhau
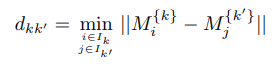
- Cặp điểm nào có khoảng cách ngắn nhất sẽ được lấy làm giá trị min.separation, coi là inter-cluster – separation
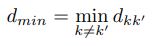
- Tính toán khoảng cách xa nhất giữa các điểm trong từng cluster với nhau
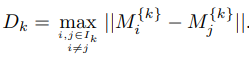
- Cặp điểm trong cluster nào có khoảng cách Dk xa nhất sẽ được lấy làm max.diameter, coi là intra-cluster – compactness/cohesion , sau cùng chúng ta sẽ lấy tỷ lệ để tìm Dunn’s Index
Vì thông thường trong một cluster chúng ta mong muốn các điểm sẽ nằm gần nhau nên diameter lý tưởng sẽ rất nhỏ, intra-cluster – compactness sẽ nhỏ. Giữa các cluster chúng ta mong muốn chúng khác biệt nhất nên separation lý tưởng sẽ rất lớn, inter-cluster – separation sẽ lớn. Như vậy Dunn’s index càng lớn càng tốt
Lưu ý: việc lấy max, min chỉ là việc chọn lựa giá trị để đưa vào phép tính chứ không có ý nghĩa nào khác.
Ví dụ, để minh họa đơn giản chúng tôi sẽ lấy lại bảng số liệu trên:
Chúng ta có 5 điểm dữ liệu:
X1 = 0 X2 = 2, X3 = 4, X4 = 6 đến X5 = 8, các điểm X1, X2, X3 giờ thuộc cluster 1, X4, X5 thuộc cluster 2
Dmin.separation = D(X3, X4) = 2
Dmax.diameter = D(X1, X3) = 4
Dunn’s Index = 2/4 = 0.5
Cách tính khoảng cách giữa các cụm hay bên trong cụm có thể sử dụng điểm trung tâm Centroid (trong k-means clustering) hoặc Complete – linkage (trong hierarchical clustering)
Davies and Bouldin Index
Phương pháp chúng tôi muốn nhắc đến sau cùng trong bài viết này là chỉ số Davies and Bouldin.
Để tính chỉ số DB, chúng ta phải đo lường mức độ phân tán và tương đồng của các cụm.
Gọi S là giá trị đo lường độ phân tán, S lớn hơn hoặc bằng 0, S = 0 nghĩa là 2 điểm dữ liệu bằng nhau và nằm trong cùng 1 cụm.
Công thức tính S:
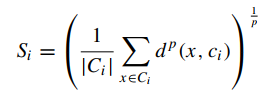
Ci là tổng số các điểm dữ liệu, số quan sát trong cụm Ci, ci là điểm trung tâm cụm, x là một điểm bất kỳ trong cụm Ci. P thường bằng 2, nếu sử dụng công thức Euclidean để tính khoảng cách giữa x đến điểm trung tâm ci, khoảng cách ngắn thì độ phân tán thấp.
Tiếp theo chúng ta sẽ đo lường điểm tương đồng Rij của 2 cluster Ci và Cj mà ở đó phải thỏa mãn các điều kiện sau:
1. Rij ≥ 0;
2. Rij = Rji;
3. Rij = 0 khi và chỉ khi Si = Sj;
4. Nếu Sj = Sk và Dij < Dik, thì Rij > Rik;
5. Nếu Sj > Sk và Dij = Dik, thì Rij > Rik.
Với Rij được tính như sau:
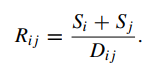
Si, Sj, Sk là độ phân tán của cụm Ci, Cj, Ck. D là khoảng cách giữa 2 cluster tính dựa trên công thức euclidean tính khoảng cách giữa 2 điểm trung tâm cụm.
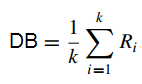
Ri = max (Rij) nếu k > 1
Nhìn vào công thức Rij, nếu độ phân tán Si và Sj thấp, các điểm dữ liệu trong cụm Ci, và Cj nằm xung quanh điểm trung tâm, và nếu Dij cao, tức Ci, Cj khác biệt nhau nhiều. Các đặc điểm đánh giá kết quả từ thuật toán clustering là chất lượng => Rij có giá trị nhỏ => DB index càng nhỏ sẽ tốt hơn
Như vậy đến đây kết thúc bài viết đánh giá thuật toán clustering. Hẹn gặp các bạn ở các bài viết khác.
Tài liệu tham khảo
“Principles of Data mining” – Max Bramer
“Cluster analysis and data mining an introduction” – R.S. King
“Data Clustering Theory, Algorithms, and Applications” – Guojun Gan, Chaoqun Ma, Jianhong Wu
“Data mining and predictive analytics” – Daniel T. Larose
“Introduction to Data mining” – Tan, Steinbach, Kumar
“DATA CLUSTERING Algorithms and Applications” – Charu C. Aggarwal, Chandan K. Reddy
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English