Quay trở lại với chủ đề Survival analysi, phân tích sống sót, phần 4 bài viết lần này chúng ta sẽ cùng nhau tìm hiểu phương pháp phi tham số (non-parametric) Log-rank kiểm tra sự khác biệt trong tỷ lệ sống sót giữa 2 tổng thể nghiên cứu mà bài viết trước BigDataUni chưa thể trình bày và giới thiệu sơ lược về Cox Proportional Hazard Model (Cox PH) – phương pháp tham số (Parametric), mô hình phổ biến được ứng dụng nhiều nhất trong việc phân tích tỷ lệ sống sót, tỷ lệ rủi ro đặc biệt là định lượng ảnh hưởng từ các yếu tố tác động, từ đó giúp các công ty, tổ chức đưa ra giải pháp phù hợp.
Link các bài viết trước cho bạn nào chưa tham khảo:
Tìm hiểu Survival analysis (P.1): Khái niệm, ứng dụng
Tìm hiểu Survival analysis (P.2): Survival và Hazard Function
Tìm hiểu về Survival analysis (P.3): Life table, Kaplan – Meier, Nelson -Aalen

Nguồn hình: wildernessawareness
Ở bài viết trước chúng ta đã tìm hiểu về Life table, Kaplan – Meier và Nelson – Aalen, các phương pháp phi tham số hỗ trợ mô tả, ước lượng tỷ lệ Survival hay Hazard cho những đối tượng nghiên cứu cụ thể.
Nhưng trong thực tế khi tiến hành phân tích, chúng ta thường xem xét đến nhiều nhóm đối tượng khác nhau ví dụ các nhóm khách hàng có thu nhập khác nhau thì tỷ lệ rời dịch vụ hay churn rate có khác nhau hay không, các nhóm bệnh nhân có độ tuổi khác nhau thì tỷ lệ tử vọng khi mắc bệnh ung thư có khác nhau hay không. Các yếu tố khác biệt như thu nhập, độ tuổi ở giai đoạn sau sẽ cực kỳ hữu ích khi chúng được đưa vào mô hình tham số để định lượng tác động và hỗ trợ phân tích sâu hơn về tỷ lệ sống sót hay rủi ro. Và một trong các mô hình tiêu biểu nhất được sử dụng chính là Cox Proportional Hazards Regression viết tắt là Cox PH mà chúng ta sẽ nói đến phần sau bài viết.
Trong các phương pháp phi tham số, đặc biệt ở mảng kiểm định, thì Log-rank bên cạnh Wilconxon Test (Peto and Peto’s, Gehan’s), Cox – F-test,… là công cụ thường xuất hiện trong các phần mềm phân tích và được các chuyên gia phân tích thường sử dụng để kiểm tra sự khác biệt trong tỷ lệ sống sót giữa hai hay nhiều nhóm khác nhau. Ở bài viết này, BigDataUni chỉ có thể giới thiệu đến các bạn phương pháp Log-rank, những cái còn lại các bạn có thể tìm hiểu ở những tài liệu khác.
Log – rank Test
Gọi Log – rank Test là phương pháp phi tham số vì nó không yêu cầu chúng ta phải đưa ra bất kỳ giả định nào về quy luật phân phối xác suất của tổng thể nghiên cứu, không yêu cầu xác định các tham số cho quá trình tính toán, và loại dữ liệu có thể dùng trong Log – rank là dữ liệu định tính, định danh ví dụ như sống/ chết, rời dịch vụ/ chưa rời dịch vụ,…. Công thức Log – rank tính giá trị kiểm định chúng tôi sắp trình bày dưới đây chính là lấy từ công thức kiểm định phi tham số Chi bình phương (Chi-square χ²) nổi tiếng trong lý thuyết thống kê.
Tuy sử dụng Chi bình phương nhưng lại có tên gọi là Log – rank test, thì lý do sâu xa đến từ việc các chuyên gia khai phá ra công thức kiểm định trong Log – rank lấy từ công thức chuyển đổi Log áp dụng cho hàm Survival. Do bài viết có giới hạn, và tính chất phức tạp nên chúng tôi sẽ không trình bày “gốc rễ” của nó mà đi thẳng vào công thức chính.
Giả sử một bệnh viện thực hiện nghiên cứu sự khác biệt trong tỷ lệ sống sót trên 2 nhóm bệnh nhân ung thư, một nhóm sử dụng biện pháp trị liệu A và nhóm còn lại là B.
Bảng dữ liệu mẫu 30 bệnh nhân dưới đây gồm 5 biến: ID – số thứ tự bệnh nhân, liệu pháp, thời gian theo dõi (tối đa 3 năm, tính theo ngày), rank – xếp hạng theo thứ tự thời gian, Censored – đối tượng bị mất dấu, không có thông tin tính từ lần cuối kiểm tra hay lần cuối kiểm tra còn sống tuy nhiên vẫn cần theo dõi thêm; trạng thái – sự kiện đã xảy ra (bệnh nhân tử vong), sự kiện chưa xảy ra (còn sống)
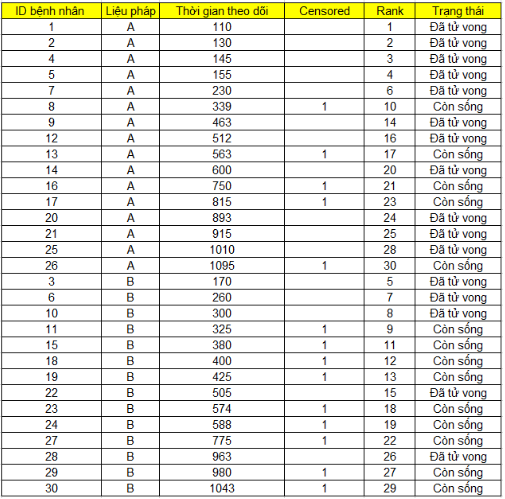
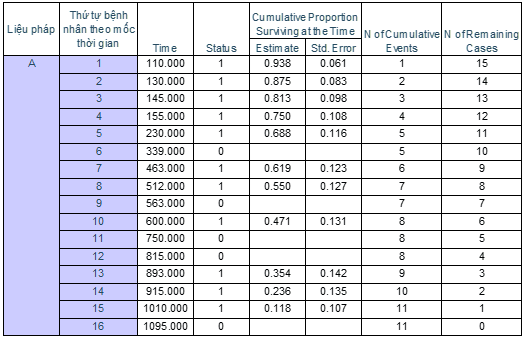
Dưới đây là kết quả ước tính tỷ lệ sống sót theo phương pháp Kaplan Meier cho nhóm A, và B mà chúng tôi giới thiệu ở bài viết trước. Các bạn nào chưa biết có thể tham khảo bài viết phần 3 của chúng tôi, link ở phía trên, tương tự Censored thì các bạn xem ở bài viết phần 1.

Đồ thị mô tả trực quan đường cong sống sót cho nhóm bệnh nhân A và B
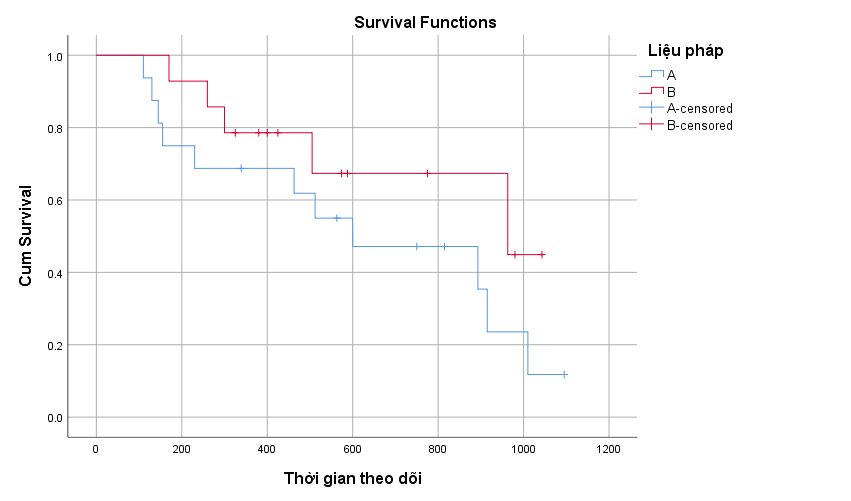
Chúng ta có thể thấy tỷ lệ sống sót tích lũy của nhóm bệnh nhân sử dụng liệu pháp B là cao hơn so với nhóm bệnh nhân sử dụng liệu pháp A. Tuy nhiên đó chỉ là mẫu dữ liệu nhỏ chỉ trên dưới 30 bệnh nhân. Để đưa ra kết luận chính xác hơn về 2 tổng thể nghiên cứu, đặc biệt là tìm hiểu thực tế liệu có sự khác biệt gì không trong tỷ lệ sống sót giữa 2 nhóm bệnh nhân này, các chuyên gia của bệnh viện sẽ phải sử dụng Log – rank.
Áp dụng Log – rank, chúng ta chỉ quan tâm đến 2 giá trị quan trọng ở mỗi mốc thời điểm đó là: số bệnh nhân có thể tử vong (Expected) và số bệnh nhân đã tử vong trong thực tế (Observed).
Công thức tính Expected như sau:
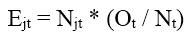
j là nhóm đang xét. ở đây j = A, B
Ot là tổng số bệnh nhân tử vong ở thời điểm t, Ot = OAt + OBt
Nt là tổng số quan sát trong mẫu còn lại ở thời điểm t, Nt = NAt + NBt
Để tính chúng ta sẽ sắp xếp lại dữ liệu theo thứ tự thời gian, giống như xếp hạng Rank ở mẫu dữ liệu trên.
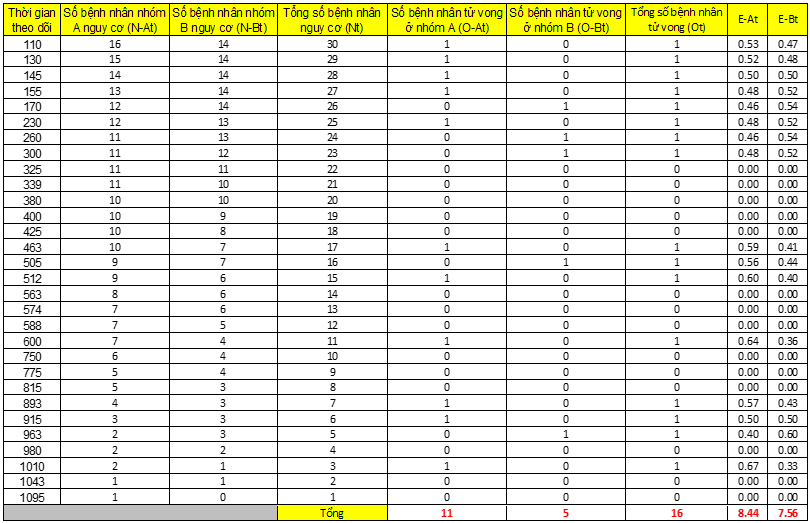
Khi tính các bạn chú ý các trường hợp Censored ở các thời điểm (xem lại bảng dữ liệu ban đầu), tuy không ghi nhận lại trên bảng nhưng số mẫu ở các nhóm sẽ có sự thay đổi. Như các bạn có thể thấy ở một số thời điểm không có bệnh nhân tử vong ở nhóm nào, nhưng đến mốc tiếp theo, số bệnh nhân ở một nhóm có thể giảm xuống, là do Censored. Đối tượng bị Censored tức chúng ta không có thông tin về đối tượng này, hay bỏ theo dõi nên sẽ không được tính vào mẫu.
Sau khi chúng ta tính được tổng OA, OB, EA, EB. Chúng ta sẽ tiến hành đặt giả thuyết và tính giá trị kiểm định Log – rank
Giả thuyết được đặt ra như sau:
H0: Không có sự khác biệt trong tỷ lệ sống sót giữa 2 nhóm bệnh nhân (SA = SB)
H1: Có sự khác biệt trong tỷ lệ sống sót giữa 2 nhóm bệnh nhân (SA ≠ SB)
Công thức kiểm định
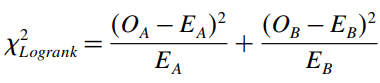
Bác bỏ H0 khi giá trị kiểm định > giá trị tra bảng Chi bình phương ở mức ý nghĩa α = 0.05, hay p – value tìm được < 0.05
Áp dụng theo công thức trên chúng ta giá trị kiểm định bằng 1.649
Tra bảng chi bình phương với bậc tự do df = số nhóm j – 1 = 2 – 1 = 1, mức ý nghĩa 0.05, chúng ta có 3.84
Giá trị kiểm định < giá trị tra bảng, nên chúng ta không có cơ sở bác bỏ H0. Cần thêm dữ liệu để phân tích và chứng minh chúng có sự khác biệt trong tỷ lệ sống sót.
Tương tự, P-value = 0.2 > α = 0.05, chúng ta sẽ không bác bỏ H0.
Lý do tại sao nói log – rank xấp xỉ giá trị kiểm định Chi bình phương. Thực chất, công thức gốc của Log – rank như sau:
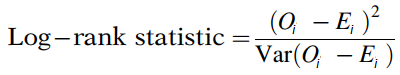
Với công thức variance
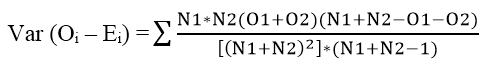
OA – EA = +2.56
OB – EB = -2.56
Chúng ta có thể lấy OA – EA hay OB – EB đều được
Var(Oi – Ei) = 3.91
Log – rank = [(2.56)^2/ 3.91] = 1.68 xấp xỉ kết quả 1.649 mà chúng ta tìm được ở trên
Kết quả từ SPSS:
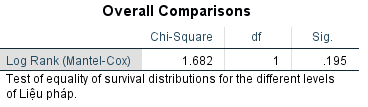
Kết luận tương tự khi giá trị kiểm định < giá trị tra bảng là 3.84, và p-value = 0.195 > 0.05, không bác bỏ H0, tức không có sự khác biệt trong tỷ lệ sống sót giữa các nhóm áp dụng liệu pháp điều trị khác nhau, cần thêm dữ liệu để phân tích thêm.
Trường hợp có nhiều hơn 2 nhóm
Công thức kiểm định:
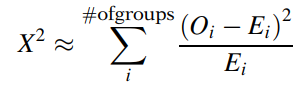
i = 1, 2, 3, ….
Chúng ta tính tổng chênh lệch (O – E)/ E của các nhóm. Lưu ý tra bảng với bậc tự do df = k – 1 với k là tổng số nhóm, và k ≥ 2
Quay trở lại với ví dụ của IBM chúng tôi có đề cập ở bài viết phần 3, chúng ta có ước tính tỷ lệ sống sót (tỷ lệ khách hàng không rời dịch vụ) theo Kaplan Meier cho 4 nhóm khách hàng như theo đồ thị dười đây.
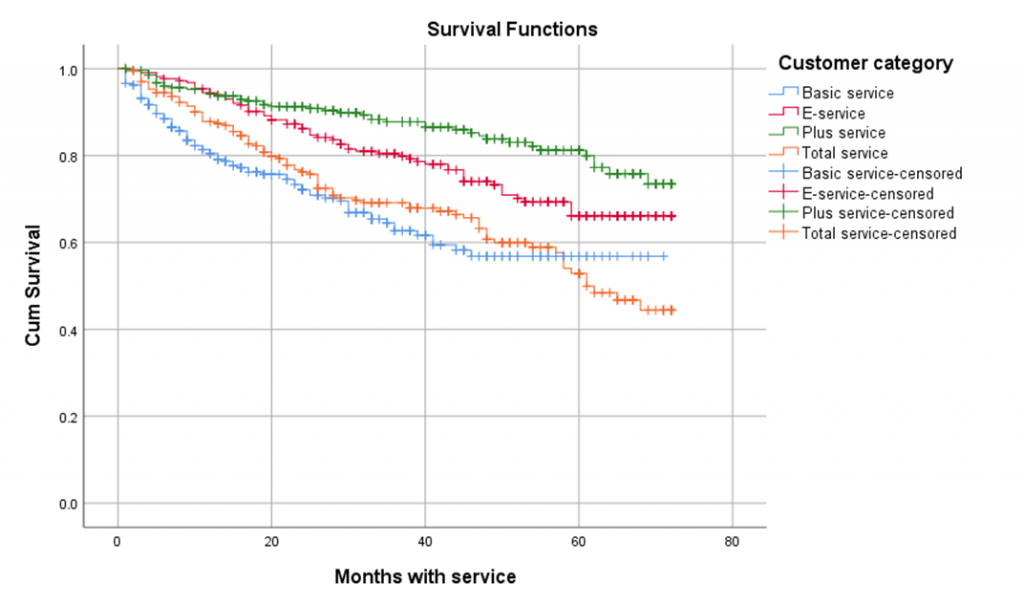
Kết quả kiểm định
Log-rank theo SPSS

P – value < 0.05, bác bỏ H0 tức có sự khác biệt trong tỷ lệ sống sót giữa các nhóm khách hàng sử dụng loại hình dịch vụ khác nhau. Do đó chúng ta có thể nhìn vào đồ thị khẳng định lại lần nữa: tỷ lệ khách hàng rời dịch vụ ở Basic Service và Total Service là khá cao, khi đường cong survival giảm mạnh và nhanh khi thời gian sử dụng tăng. Plus Service là có tỷ lệ churn thấp nhất khi đường cong survival giảm với tốc độ chậm, với mức độ rất nhỏ.
Có thể suy ra yếu tố loại hình dịch vụ được xem là yếu tố có tác động lên tỷ lệ rời dịch vụ của khách hàng, và yếu tố này có ý nghĩa để phân tích.
Khi được hỏi về việc xây dựng một mô hình mà ở đó sử dụng các yếu tố giống như loại hình dịch vụ ở trên để đánh giá nguy cơ rời dịch vụ của khách hàng thì các chuyên gia thường đề cập đến phương pháp Cox Proportional Hazard Regression (Cox PH model)
Cox Proportional Hazard Regression (Cox PH model)
Ở bài viết phần 3, chúng tôi đã giúp các bạn phân biệt giữa mô hình tham số (Parametric) và phi tham số (Non-parametric) cũng như đề cập đến các phương pháp phi tham số trong việc ước lượng tỷ lệ rủi ro hay sống sót cho các đối tượng nghiên cứu, và mô hình Cox PH chúng ta quan tâm trong bài viết lần này không được coi hoàn toàn là môt hình phi tham số cũng không được xem hoàn toàn là một hình tham số.
Theo các chuyên gia, mô hình Cox PH chính là một dạng Semiparametric có một nửa tính chất tham số và một nửa tính chất phi tham số.
Lấy lại ví dụ ở phía trên
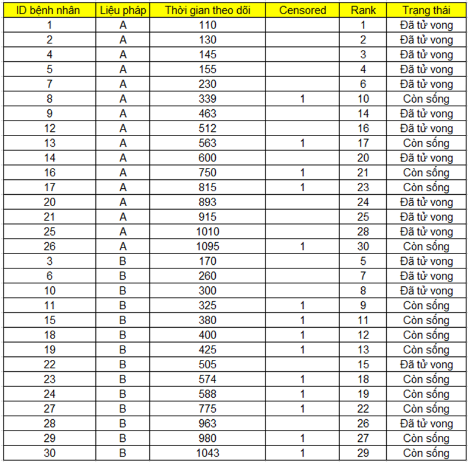
Giả sử chúng ta đang đi nghiên cứu nên xây dựng mô hình ước tính nguy cơ tử vong hay số ngày sống sót trung bình của các bệnh nhân ung thư. Ở đây biến thời gian sẽ là biến mục tiêu và nó là biến định lượng. Mô hình đơn giản nhất có thể sử dụng là hồi quy tuyến tính (Linear regression)
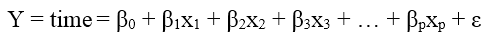
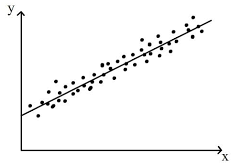
Tuy nhiên khi biến mục tiêu thời gian sống sót luôn mang giá trị dương > 0, nếu chọn mô hình như mô hình hồi quy tuyến tính vẫn có thể khiến cho giá trị này bị âm, và khiến nó không có ý nghĩa phân tích.
Do đó để đảm bảo trường hợp giá trị tìm được không bị âm, các chuyên gia thay vì sử dụng hồi quy tuyến tính, họ áp dụng hồi quy phi tuyến dạng hàm mũ, và tiến hành giả định thời gian sống sót tuân theo quy luật phân phối Exponential
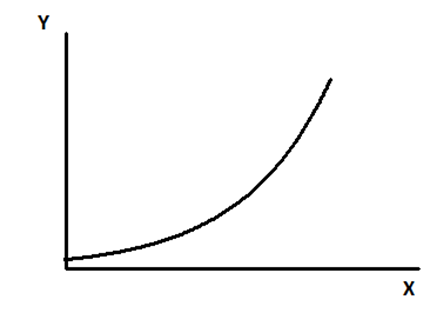
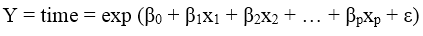
Điểm quan trọng là mô hình hồi quy tuyến tính hay phi tuyến tính chỉ tập trung vào biến thời gian lại không tập trung vào biến kết quả, do biến này là biến định danh, biến thay phiên chứ không phải biến định lượng.
Hơn nữa, trong Survival analysis, ở bài viết phần 2 khi nói về 2 hàm quan trọng Survival function và Hazard function, chúng tôi có nhấn mạnh mục đích của phân tích không phải nằm ở tìm hiểu thời gian cho đến khi sự kiện xảy ra mà đó là tính toán tỷ lệ rủi ro, tỷ lệ sống sót. Do đó, nếu chỉ tập trung vào thời gian là chưa đủ, phải xem xét thêm tỷ lệ rủi ro.
Việc xây dựng mô hình với biến mục tiêu là thời gian còn tiềm ẩn vấn đề khác. Đó là “sự vận động theo thời gian”. Nói dễ hiểu, trong thực tế có các biến X, có các thuộc tính, yếu tố có sự gia tăng hay giảm dần theo thời gian, phụ thuộc vào thời gian.
Ví dụ, khách hàng mua hàng của một công ty, mỗi lần mua hàng thường chi số tiền ít, không nhiều, nhưng mua hàng nhiều lần, trải dài qua các tháng, nghĩa là số tiền chi ra tăng theo thời gian, khách hàng ở lại lâu hơn với công ty, và rủi ro rời dịch vụ thấp dần. Tuy nhiên có trường hợp khác, một khách hàng mua hàng ít lần hơn, nhưng số tiền bỏ ra nhiều hơn cho mỗi lần, các lần mua hàng thường gần nhau không trải dài. Vậy liệu có thể khẳng định vị khách này có khả năng rời dịch vụ cao hơn? Sự tăng lên trong chi tiêu có thể có hoặc không phụ thuộc vào thời gian.
Nhưng nếu chúng ta đưa vô mô hình với biến mục tiêu là Time thì chính biến “chi tiêu” khả năng sẽ không còn ý nghĩa phân tích, nó có thể vô tình trở thành điều hiển nhiên, chi tiêu nhiều nghĩa là khách hàng trung thành hơn với công ty, ngộ nhận chi tiều nhiều là do thời gian tăng. Và điều này không hoàn toàn hợp lý!
Mặc dù biết rằng, chúng ta phải xem xét thêm các biến khác như lần mua hàng gần nhất, số lần mua để đánh giá chính xác hơn, tuy nhiên, khi đi sâu phân tích mối quan hệ giữa riêng biến chi tiêu với tỷ lệ rủi ro cần có sự cân nhắc kỹ lưỡng, khoan đưa ra kết luận vội vã.
Do đó, để tránh sự ảnh hưởng của việc các biến“vận động theo thời gian” lên kết quả đạt được, chúng ta không nên xây dựng mô hình với biến mục tiêu là Time, thay vào đó là tỷ lệ rủi ro, và tách biệt thành 2 phần: tỷ lệ rủi ro theo thời gian, và tỷ lệ rủi ro theo các biến (các biến có hay không phụ thuộc thời gian)
Mặt khác các bạn cũng đã biết thời gian theo dõi có thể cho chúng ta biết khi nào sự kiện xảy ra, khi nào bệnh nhân chết, khi nào khách hàng rời dịch vụ tuy nhiên nó lại không cho chúng ta biết đối tượng nào bị Censored, bị mất dấu, nguy hiểm là nhầm lẫn tai hại giữa thời gian theo dõi, và thời điểm sự kiện xảy ra.
Lấy ví dụ, nếu chúng ta phớt lờ biến trạng thái, biến censored chỉ tập trung vào biến time thì có phải các bạn sẽ đều nghĩ chúng là thời điểm tử vong của bệnh nhân? Mặt khác, nếu chúng ta chỉ chăm chăm vào thời gian tử vong, và cho rằng tỷ lệ tử vong là không đổi (bệnh nhân nào cũng sẽ đối mặt với cái chết, quan trọng là sớm hay muộn), là như nhau mà không xem xét đến thời gian sống sót, thì đã đi sai hướng trong Survival analysis.
Chúng ta phải tìm ra mô hình hỗ trợ chúng ta phân tích được tỷ lệ rủi ro theo thời gian, và ước tính được tỷ lệ rủi ro dựa trên các yếu tố tác động khác ngoài thời gian. Vậy chúng ta nên chọn mô hình nào là hợp lý?
Như vậy một mô hình tham số phân tích hoàn chỉnh trong Survival analysis chúng ta sẽ có 2 phần chính:
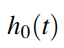
Và:
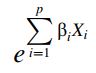
Với h0(t) được gọi là Baseline Hazard function, hàm Hazard theo thời gian hay đường Hazard cơ sở theo thời gian. Như chúng tôi nói ở trên chúng ta không thể bỏ qua tỷ lệ rủi ro theo thời gian. Baseline hazard được hiểu là mỗi đối tượng nghiên cứu trong tổng thể sẽ cùng có một tỷ lệ rủi ro. Và tỷ lệ rủi ro này có thể tăng, giảm, hay không đổi phụ thuộc vào thời gian.
Nói một chút về h0(t), chúng ta không thể sử dụng các phương pháp phi tham số như Kaplan Meier, Life – table, hay Nelson – Aalen. Do các phương pháp này giả định là các biến, các yếu tố tác động là chưa biết, không định lượng chính xác, chứ không phải là không có. Còn h0(t) ở đây là Baseline Hazard được tính toán dựa trên điều kiện là hoàn toàn không có sự xuất hiện của các biến X. Cần dùng phương pháp khác để ước lượng.
Điều may mắn mà theo các chuyên gia khi họ sử dụng Cox PH đó là chúng ta không cần đưa ra bất kỳ giả định gì về quy luật phân phối, hay không phải xác định bất kỳ tham số, cũng như mô hình nào cho nó, đặc biệt là không cần ước lượng h0(t). Nói cách khác, khi sử dụng Cox PH, mục đích chỉ để phân tích tác động của những yếu tố mà chúng ta cho rằng có thể ảnh hưởng lên tỷ lệ rủi ro sau cùng. Hơn nữa, các phần mềm phân tích như SPSS, Stata,… đều tính sẵn vào khi chúng ta tiến hành tính toán tỷ lệ rủi ro theo mô hình Cox PH tìm được.
Tính chất này giống Non – parametric – phi tham số, nên đây cũng là lý do tại Cox PH được coi là Semi – Parametric.
Ở phần thứ hai, hàm mũ e, các biến X đại diện cho các yếu tố tác động lên tỷ lệ rủi ro được định lượng bởi các hệ số hồi quy β. Chúng sẽ ảnh hưởng khiến tỷ lệ rủi ro thay đổi. Lưu ý các biến X này độc lập với thời gian, và không phụ thuộc vào thời gian, xét trong mô hình dưới đây. Trường hợp các biến X có mối liên hệ với thời gian, chúng ta sẽ có mô hình khác để phân tích, cụ thể ở bài viết tới chúng tôi sẽ đề cập.
Phương trình tổng quát:

Đến đây nhiều bạn sẽ thắc mắc tại sao chúng ta không coi thời gian theo dõi đối tượng là một biến X và đưa vào mô hình để ước tính h(t) thay vì tách riêng ra h0(t) – tỷ lệ rủi ro theo thời gian t? Giải thích đơn giản, chúng ta không thể đảm bảo liệu các biến X trước đó có mối liên hệ gì với thời gian hay không, giống ví dụ ở trên về số tiền chi tiêu của khách hàng. Nếu chúng có mối liên hệ, thì nguy cơ mô hình hồi quy bị đa cộng tuyến (Multicollinearity) và kết quả phân tích có được từ mô hình sẽ bị ảnh hưởng.
Thứ hai, nếu đưa thời gian vào mô hình hàm mũ tức chúng ta đang giả định thời gian xảy ra sự kiện cũng như tỷ lệ rủi ro theo thời gian tuân theo quy luật phân phối dạng hàm mũ (Exponential distribution) trong khi thực tế chúng ta không biết có đúng như vậy không.
Đó là lý do chúng ta cần có h0(t), nó là hàm rủi ro theo thời gian, cho chúng ta biết được tỷ lệ rủi ro sẽ như thế nào theo thời gian mà không bị các yếu tố X ảnh hưởng, nó có thể có bất kỳ quy luật phân phối nào và không yêu cầu chúng ta phải giả định.
Giải thích thêm về lý do vì sao sử dụng mô hình hồi quy hàm mũ. Thì bên cạnh đảm bảo tỷ lệ rủi ro không mang giá trị âm, lý do khác đó là mối quan hệ giữa f(t) hàm mật độ xác suất cho t là thời gian sự kiện xảy ra, h(t) là hàm rủi ro tại thời điểm t và H(t) hàm rủi ro tích lũy tính đến thời điểm t.
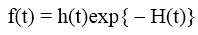
Theo công thức trên, thời gian xảy ra sự kiện có hàm mật độ f(t) là một dạng hàm mũ
Mô hình hàm mũ cho phép chúng ta giả định h0(t) là một hằng số không đổi theo thời gian, đơn giản quá trình tính toán hay phân tích. Đây là tính chất của hồi quy hàm mũ nói chung. Các bạn nào chưa biết thì đây là phương trình tổng quát của Exponential Regression: Y = a*eβx
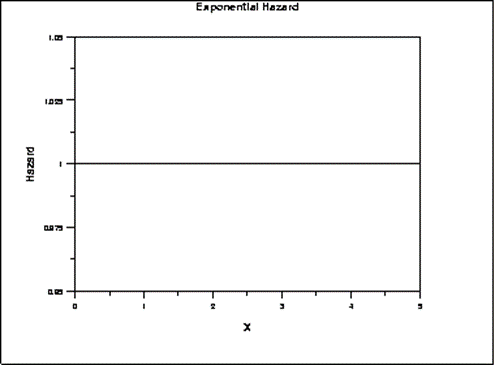
Trên hình là ví dụ đường baseline Hazard không đổi theo thời gian khi mô hình áp dụng là Exponenetial.
Ví dụ, trong một thử nghiệm lâm sàng, điều này có nghĩa là tỷ lệ tử vong cơ bản trong năm đầu tiên theo dõi bệnh nhân bằng với tỷ lệ tử vong trong mỗi năm tiếp theo. Tuy nhiên nó lại không đúng ở một số trường hợp như ví dụ một bệnh nhân có khối u, tiến hành phẫu thuật, có 2 khả năng xảy ra bệnh nhân có thể chết trong lúc phẫu thuật và nếu sống sau khi kết thúc phẫu thuật, thì có thể khỏi bệnh hoàn toàn. Thế nhưng nếu theo mô hình hàm mũ, tỷ lệ rủi ro vẫn có thể tăng, tức trong tương lai, khối u sẽ xuất hiện trở lại, và khiến cho bệnh nhân lại phải đối mặt với tình huống sống còn? Đúng hơn ở trường hợp này đường cong có chiều hướng đi lên (từ lúc bệnh nhân mắc bệnh cho đến khi phẫu thuật) và có chiều hướng đi xuống (kể từ khi bệnh nhân phẫu thuật thành công)
Cũng chính vì có các trường hợp đặc biệt trên, nên trong mô hình Cox PH, thường có ý kiến cho rằng không cần đưa ra bất kỳ giả định gì cho h0(t) mặc dù khi ghép vào phương trình hồi quy hàm mũ, theo lý, nó phải giữ nguyên qua thời gian. Do đó mô hình Cox PH được nói vui là mô hình hồi quy Exponential “nửa vời”.
Bên cạnh Exponential regression, còn có các mô hình khác như Weibull, Gompertz và log-normal,…Bạn nào quan tâm có thể xem ở các tài liệu khác.
Phương trình không có intercept
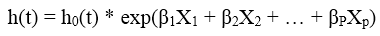
Khác với các mô hình hồi quy thông thường có β0 còn gọi là intercept, là giá trị của biến mục tiêu Y khi các biến X = 0. Ở trường hợp Cox PH, khi các X bằng 0 chúng ta sẽ có h(t) = h0(t)*exp(β0), do exp(β0) không đổi nên nó được nhân thẳng vào h0(t) tạo thành h0(t)’ là Baseline hazard mới để đơn giản hóa mô hình. Đây cũng là lý do kết quả Cox PH từ SPSS, Stata đều không có thông tin về β0.
Phương trình trên là phương trình tổng quát cho Cox PH, dạng mô hình nhân (Multiplicative), Baseline function cùng với các hệ số hồi quy hay tác động của biến X không đổi theo thời gian. Mô hình cộng – Additive thì phần hàm mũ sẽ đóng vai là phần thêm vào hay bổ sung, các hệ số hồi quy hay tác động của biến X được phép thay đổi theo thời gian, phù hợp khi chúng ta quan tâm về sự khác biệt về lượng trong tỷ lệ rủi ro, thay vì tính theo tương đối (% tăng giảm)
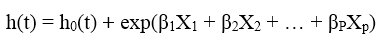
Ngoài ra còn có mô hình mix giữa 2 loại đó là mô hình Additive – Multiplicative, khi chúng ta có cả các biến có tác động thay đổi theo thời gian, và không thay đổi theo thời gian. Trong phạm vi series bài viết đầu tiên về Survival, chúng ta chỉ tập trung vào mô hình nhân mà thôi
Chúng ta đã nói khá nhiều về h0(t) mà chưa nó gì về hệ số hồi quy β được hiểu như thế nào.
Giả sử chúng ta có mô hình Cox PH dự báo tỷ lệ khách hàng rời dịch vụ như sau:
h(t) = h0(t)*exp(0.6712*x1 + 0.1190*x2 – 0.4789*x3)
Các bạn lưu ý lần nữa cách viết: ex = exp(x)
Các hệ số hồi quy trong Cox PH có nhiệm vụ giống như hệ số hồi quy trong các mô hình hồi quy bình thường, có vai trò định lượng mức tăng thêm hay giảm đi trong giá trị của biến mục tiêu khi các biết dự báo, biến X thay đổi 1 đơn vị.
X1 là biến độ khoảng thời gian tính từ lần mua hàng gần nhất (năm), biến X2 là giới tính (1: nam, 2: nữ), X3 là thu nhập hàng tháng đơn vị triệu đồng.
- Với hệ số hồi quy 0.6712, khi thời gian tính từ lần mua hàng gần nhất tăng lên 1 năm, thì tỷ lệ rủi ro khách hàng rời dịch vụ sẽ tăng lên (exp(0.6712) – 1)*100% = (e0.6712 – 1)*100% = 95%. Hoặc tỷ lệ rời dịch vụ của một khách hàng có thời hạn kể từ lần cuối mua hàng nhiều hơn 1 năm so với các khách hàng khác sẽ cao gấp 1.95. Trong điều kiện các biến khác đang ở trạng thái “đứng yên”, giữ nguyên không đổi.
- Với hệ số hồi quy 0.1190, nếu khách hàng là giới tính nam thì tỷ lệ rời dịch vụ sẽ tăng e0.119 – 1 = 1.12 – 1 = 0.12 tức tăng 12%. Hoặc tỷ lệ rời dịch vụ của khách hàng nam cao gấp 1.12 lần so với khách hàng nữ. Trong điều kiện các biến khác đang ở trạng thái “đứng yên”, giữ nguyên không đổi.
- Với hệ số hồi quy – 0.4789, nếu thu nhập của khách hàng tăng 1 triệu VND, thì tỷ lệ rời dịch vụ sẽ giảm e– 0.4789 – 1 = – 0.38 tức giảm 38%, hoặc tỷ lệ rời dịch vụ của khách hàng có thu nhập cao hơn 1 triệu so với khách hàng khác sẽ nhỏ hơn gấp 0.62 lần. Trong điều kiện các biến khác đang ở trạng thái “đứng yên”, giữ nguyên không đổi.
Tại sao phải dùng đến exp() để giải thích? Hay nói cách khác hệ số hồi quy β có mối quan hệ như thế nào với tỷ lệ rủi ro? Hệ số hồi quy β được ước tính bằng phương pháp gì? Chúng tôi sẽ trình bày cụ thể hơn ở các bài viết sắp tới, cùng với các công thức tính toán, công thức kiểm định quan trọng trong Cox PH.
Tài liệu tham khảo:
“Survival Analysis” – Lisa Sullivan
“An Introduction to Survival Analysis” – Mario Cleves và cộng sự
“Survival Analysis A Practical Approach” – David Machin và cộng sự
“Survival Analysis – Models and Applications” – Xian Liu và cộng sự
“Analysis of Survival data” – D.R.Cox và cộng sự
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English