Ở bài viết trước, chúng ta đã tìm hiểu các phương pháp kiểm định tham số trường hợp 1 mẫu, kiểm định các giả thuyết của một đặc trưng của một đối tượng nghiên cứu trong tổng thể, với các công thức, ví dụ diễn giản cụ thể. Trong bài viết cuối về kiểm định tham số, BigDataUni và các bạn cùng đi tiếp đến những dạng kiểm định khác áp dụng cho trường hợp 2 mẫu dữ liệu.
Như thường lệ, xin lưu ý, các bạn nào chưa có kiến thức gì về thống kê nói chung hay tổng quan về phương pháp kiểm định nói riêng thì không thể nắm bắt những nội dung trong bài viết này. Các bạn có thể tham khảo ở những tài liệu khác hay các bài viết của chúng tôi theo link dưới đây. Nội dung bài viết này là phần tiếp nối bài viết trước, nên chúng tôi sẽ không nhắc lại các kiến thức đã đề cập.
Tổng quan về Statistics: Khái niệm và ứng dụng của thống kê
Tổng quan về Statistics: Descriptive statistics (thống kê mô tả)
Tổng quan về Statistics: Inferential statistics (thống kê suy luận)
Tìm hiểu về phương pháp kiểm định tham số
Các dạng kiểm định tham số (trường hợp 1 mẫu)
Trong bài viết đầu tiên về phương pháp kiểm định tham số – Hypothesis test – chúng tôi đã nói đến cách phân loại các dạng kiểm định: theo số lượng mẫu, kích thước mẫu, theo đặc trưng tổng thể nêu ra trong giả thuyết, lần này là phân loại theo mục đích nghiên cứu.
Phương pháp kiểm định tham số được phân làm 2 loại chính: kiểm định các giả thuyết về một đặc trưng của đối tượng nghiên cứu trong tổng thể (kiểm định trên 1 mẫu), kiểm định sự khác biệt của một đặc trưng về một đối tượng nghiên cứu khi có hoặc không có yếu tố tác động hoặc kiểm định sự khác biệt giữa hai đối tượng nghiên cứu về một đặc trưng nào đó (kiểm định trên 2 mẫu). Tóm lại là kiểm định giả thuyết về đặc trưng của tổng thể, và kiểm định giả thuyết về sự khác biệt.
Trong thực tế, loại thứ 2, thường phổ biến hơn vì lợi ích mà nó mang lại trong kinh doanh là khá rõ ràng ví dụ thử nghiệm các phương pháp sản xuất mới, đánh giá hiệu quả của sản phẩm khi thay đổi dây chuyền sản xuất, đánh giá hiệu quả chiến dịch marketing tại cửa hàng và kênh thương mại điện tử, kiểm chứng sự khác biệt giữa đối tượng khách hàng nam và nữ khi sử dụng sản phẩm nước hoa mới, tiến hành kiểm tra giả thuyết để xác định xem có bất kỳ sự khác biệt nào xuất hiện giữa tỷ lệ các bộ phận bị lỗi trong tất cả sản phẩm được cung cấp bởi công ty A so với tỷ lệ các bộ phận bị lỗi trong tất cả các sản phẩm công ty B cung cấp. Hay ở lĩnh vực xã hội, kiểm định sự khác biệt về mức lương khởi điểm khi bắt đầu đi làm giữa dân số nam và nữ,..
Những phương pháp kiểm định tham số liên quan các vấn đề về sự khác biệt phân tích trên 2 hay nhiều mẫu từ cơ bản đến nâng cao, tuy thuộc về lĩnh vực thông kê, nhưng cũng được ứng dụng nhiều trong Data mining và Data analytics với mục đích hỗ trợ xây dựng các thuật toán.
Phương pháp kiểm định tham số trên 2 mẫu có điểm chung với phương pháp kiểm định 1 mẫu là đều đề cập về các tham số của tổng thể như trung bình, tỷ lệ tổng thể,… trong các giả thuyết được đặt ra, có điểm khác biệt chính, là ở 2 mẫu chúng ta sẽ có đến 2 tham số µ1, µ2 và p1, p2 của 2 tổng thể thay vì µ0, p0 như kiểm định 1 mẫu
Tại sao lại cần kiểm định các vấn đề về sự khác biệt?
Ở đoạn đầu bài viết chúng tôi có liệt kê những ví dụ khi nào áp dụng kiểm định 2 mẫu, để làm rõ hơn chúng tôi sẽ minh họa cụ thể hơn cho các bạn, trong lĩnh vực kinh tế.
Đối với các công ty trong lĩnh vực thương mại điện tử như Amazon, hay các công ty cung cấp các nền tảng giải trí trực tuyến như Netflix mà chúng tôi đề cập ở các bài viết ứng dụng phân tích dữ liệu trong ngành giải trí truyền thông, thì việc thiết kế một website đẹp mắt thu hút khách hàng tương tác, giao dịch là cực kỳ quan trọng. Ví dụ để thu hút khách hàng mua hàng, các công ty thương mại điện tử khi thiết kế nút mua hàng sao cho tăng được tỷ lệ chuyển đổi, tức có bao nhiêu khách hàng sau khi tìm kiếm dựa trên nhu cầu của mình và nhìn thấy sản phẩm, dịch vụ, thì họ sẽ click vào nút “Thêm vào giỏ hàng” chẳng hạn? Nếu bạn nào hay đặt mua hàng từ Lazada hay Tiki, chắc đã quá quen thuộc. Giả sử một chuyên viên thiết kế phối hợp với chuyên viên marketing, thực hiện nhiều bản mẫu và chọn lựa trên phương pháp testing A/B, cuối cùng quyết định thiết kế nút Call-to-action là màu đỏ, hình chữ nhật, bo tròn 4 đầu.


Kết thúc thử nghiệm sau 1 tháng, với các dữ liệu thu thập được từ thử nghiệm, và dữ liệu lịch sử khi áp dụng button cũ, câu hỏi đặt ra:
- Làm cách nào dựa trên dữ liệu chúng ta so sánh được chính xác thiết kế button nào sẽ tăng tỷ lệ khách hàng click vô, cái nào hiệu quả hơn, có khả năng thu hút mọi khách hàng tốt hơn?
- Và bằng cách nào chúng ta sẽ biết được xét trong tất cả các khách hàng (tổng thể nghiên cứu), những khách hàng mới sau này, những khách hàng cũ quay lại, thì khả năng họ click vào button có cao hơn button cũ hay không? Dự báo xác suất click vào button mới so với button cũ sau lần truy cập đầu tiên vào page sản phẩm có cao hơn?
- Cuối cùng có cơ sở nào kết luận có sự khác biệt giữa 2 thiết kế trong việc thu hút khách hàng, và cái nào chắc chắn hiệu quả hơn?
Phương pháp kiểm định tham số với giả thuyết thống kê xét trên 2 mẫu (ở ví dụ này, mẫu 1: dữ liệu khách hàng truy cập website trước khi đổi button và mẫu 2: dữ liệu khách hàng truy cập website sau khi đổi button). 2 mẫu này là độc lập, do đặc điểm và tính chất cũng như về số lượng các khách hàng truy cập website trước khi có button mới sẽ hoàn toàn khác so với sau khi có button mới. Mỗi mẫu sẽ được dùng để đánh giá độ hiệu quả cho mỗi button.
Đó là ví dụ trong lĩnh vực kinh tế còn ở lĩnh vực khác thì sao?
Ở thời điểm hiện tại, từ “Covid-19” chắc chắn đã quá phổ biến trên toàn thế giới, lý do chính là hậu quả mà dịch bệnh này để lại là thực sự khủng khiếp đối với hầu hết tất cả các quốc gia, và nước ta cũng không ngoại lệ. Từ giáo dục, đến kinh tế, mọi lĩnh vực đều bị ảnh hưởng bởi dịch bệnh.
Các học sinh, sinh viên ngày nay thường phải học trực tuyến thay vì đến trường, tập trung đông người sẽ dẫn đến nguy cơ lây lan cao. Vấn đề đặt ra hầu hết ở mọi nước hiện tại khi buộc các trường học triển khai học trực tuyến thì liệu có ảnh hưởng kết quả học tập của học sinh hay không? Liệu chương trình, kế hoạch giảng dạy trực tuyến đã đáp ứng nhu cầu của phụ huynh hay không, trên cơ sở tiền học phí đã đóng?
Bỏ qua vấn đề học phí, hiện nay các trường học và cả học sinh đều quan tâm nhiều hơn đến việc tiếp thu kiến thức, kết quả học tập sau cùng. Giả sử, một trường đại học về kinh tế muốn biết khi áp dụng hình thức học trực tuyến thì kết quả học tập có bị ảnh hưởng không, giả định format thi, và độ khó đề thi không thay đổi. Ví dụ các thầy cô sẽ phải thu thập dữ liệu kết quả thi trước học kỳ trước, trước khi áp dụng học trực tuyến, và dữ liệu kết quả thi học kỳ này sau khi áp dụng học trực tuyến, của một lớp học bất kỳ và theo dõi. Câu hỏi đặt ra:
- Điểm số trung bình của một sinh viên bất kỳ trong lớp học này sau khi áp dụng học trực tuyến có sự khác biệt đối với cách học thông thường không?
- Xu hướng điểm số trung bình sẽ tăng hay giảm, để đánh giá việc học trực tuyến có tốt hơn để áp dụng linh hoạt các chương trình giảng dạy trong tương lai?
- Cuối cùng, có thể đánh giá hình thức học trực tuyến có ảnh hưởng đến kết quả học tập trên phạm vi toàn trường, ở tất cả các khoa, các khóa, các lớp để ra quyết định xem xét và cải thiện.


Phương pháp kiểm định trên 2 mẫu lúc này sẽ được áp dụng, với mẫu 1 là dữ liệu kết quả thi trước khi áp dụng học trực tuyến, mẫu 2 là dữ liệu kết quả thi sau khi áp dụng học trực tuyến, tuy nhiên khác với ví dụ kinh tế ở trên. 2 mẫu này là mẫu cặp, lý do, số sinh viên trong lớp học, về đặc điểm, tính chất, và số lượng trước khi áp dụng học trực tuyến và sau khi áp dụng học trực tuyến là như nhau. Đối tượng nghiên cứu duy nhất ở đây là phương pháp học trực tuyến. Và cả 2 mẫu này phải được dùng để đánh giá hiệu quả về phương pháp học trực tuyến, không thể tách biệt.
Các dạng kiểm định 2 mẫu
Mục đích chúng tôi đề cập các ví dụ thực chất là muốn các bạn hiểu rõ hơn về các dạng kiểm định 2 mẫu mà chúng ta sẽ đi qua trong bài viết này.
Ở ví dụ 1, khi muốn đánh giá độ hiệu quả của 2 button áp dụng trong website thương mại điện tử, chúng ta sẽ xem tỷ lệ chuyển đổi của 2 button (tức tỷ lệ khách hàng sẽ click vào button đó khi lần đầu truy cập website) và tiến hành phân tích. Vậy chúng ta có dạng đầu tiên là kiểm định sự khác biệt giữa 2 tỷ lệ.
Ở ví dụ 2, khi muốn đánh giá độ hiệu quả của việc áp dụng phương pháp học trực tuyến thời Covid-19, các thầy cô sử dụng điểm trung bình từ kết quả thi của các sinh viên trước và sau khi áp dụng học trực tuyến để so sánh. Vậy chúng ta có dạng tiếp theo là kiểm định sự khác biệt giữa 2 giá trị trung bình.
Ngoài ra còn có dạng kiểm định sự khác biệt của 2 phương sai nhưng dạng này ít phổ biến trong thực tế nên chúng tôi không đề cập, các bạn có thể tham khảo các tài liệu khác.
Nếu xét về mẫu, thì như đã nói ở trên, ví dụ 1 là 2 mẫu độc lập, ví dụ 2 là mẫu cặp. Chúng ta sẽ có 2 dạng kiểm định 2 mẫu trường hợp 2 mẫu là độc lập, và 2 mẫu là mẫu cặp.
Lưu ý cách phân biệt mẫu cặp và 2 mẫu độc lập sẽ dựa trên tính chất và đặc điểm của các quan sát có trong 2 mẫu, nếu các quan sát hoàn toàn giống nhau (về đặc điểm, và số lượng,..) ở 2 mẫu, thì khả năng cao là mẫu cặp, còn không thì ngược lại.
Các công thức và ví dụ cụ thể
Dạng 1: kiểm định giả thuyết về sự khác biệt giữa 2 trung bình tổng thể.
Chúng ta sẽ đặt giả thuyết như sau:
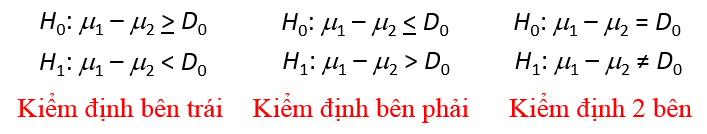
D0 chính là sự khác biệt, sự chênh lệch giữa 2 giá trị trung bình.
Ví dụ nếu nói điểm trung bình của một sinh viên lớp A bất kỳ trước và sau khi áp dụng phương pháp học trực tuyến là khác nhau nhưng không xác định cụ thể là bao nhiêu, chúng ta sẽ đặt giả thuyết với D0 = 0, µ1 là điểm trung bình của một học sinh lớp A trước khi áp dụng học online, µ2 là sau khi đã áp dụng
H0: µ1 – µ2 = 0
H1: µ1 – µ2 ≠ 0
Ví dụ nếu nói điểm trung bình của một sinh viên lớp A bất kỳ sau khi áp dụng phương pháp học trực tuyến thấp hơn 1.5 điểm so với trước khi học trực tuyến, lúc này D0 = 1.5. tức µ2 sẽ thấp hơn µ1 1.5 điểm, đây là kiểm định bên phải, nếu ngược lại sẽ là kiểm định bên trái
H0: µ1 – µ2 ≤ 1.5
H1: µ1 – µ2 > 1.5
Trường hợp 1: độ lệch chuẩn của cả 2 tổng thể nghiên cứu đã biết, và 2 mẫu độc lập lớn, số quan sát ở 2 mẫu > 30
Ở bài viết trước chúng tôi đã có nói khi điều kiện thông tin về độ lệch chuẩn của tổng thể là không thỏa mãn, thì công thức kiểm định, và quy luật phân phối xác suất sẽ khác nhau, tương tự như quy tắc bác bỏ, cách tra bảng và tính p-value.
Nhắc lại bạn nào chưa biết gì về những gì chúng tôi nói ở trên và dưới đây, vui lòng nghiên cứu trước kiểm định tham số trường hợp 1 mẫu ở các tài liệu khác hoặc tham khảo các bài viết trước của chúng tôi, link bài viết để ở phần đầu. Chúng tôi sẽ không đề cập lại kiến thức cũ
Nếu chúng ta biết trước độ lệch chuẩn, chúng ta sẽ sử dụng công thức kiểm định 2 mẫu là công thức kiểm định Z, quy luật phân phối chuẩn tắc, và tra bảng Z để tìm Zα hoặc Zα/2
Công thức kiểm định:
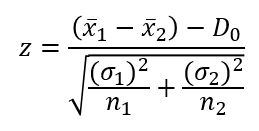
Quy tắc bác bỏ cũng tương tự kiểm định 1 mẫu:
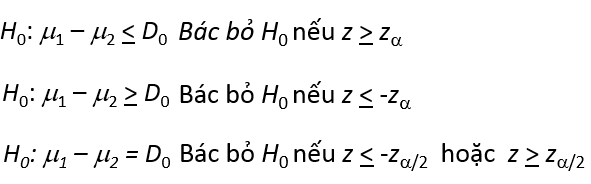
Cách tra bảng Z để tìm Zα hoặc Zα/2 cũng như cách tính p-value, và kiểm tra bác bỏ trên đồ thị hàm số các bạn xem lại bài viết trước.
Quy tắc bác bỏ dựa trên p-value:
Nếu quy định trước một mức ý nghĩa α nào đó thì:
- p-value ≤ α thì bác bỏ giả thuyết H0, chấp nhận H1
- p-value > α thì chưa có cơ sở bác bỏ H0
Chúng ta cùng đi qua ví dụ:

Một công ty kinh doanh bánh kẹo (cả sản xuất và nhập khẩu) quy mô vừa tại thành phố Hồ Chí Minh triển khai các hoạt động thương mại điện tử, và bán hàng online trên website của mình. Việc xây dựng website, từ thiết kế cấu trúc cho đến thiết kế hình ảnh, nội dung quảng cáo, bảo trì web, kiểm soát web trước giờ đều thuê một agency bên ngoài (hình thức outsource). Đến nay website đã chính thức vận hành được 1 năm. Tuy nhiên vấn đề đặt ra, agency bên ngoài thường không hiểu rõ sản phẩm, dịch vụ, giá trị cốt lõi, mong muốn, mục đích kinh doanh của công ty, hơn nữa họ không hiểu hành vi, nhu cầu khách hàng. Vì vậy khi triển khai một chiến dịch marketing quy mô lớn, hay cho ra mắt những sản phẩm mới thuộc dòng sản phẩm chính, và đưa nội dung mới lên website, đội ngũ marketing công ty phải “phối hợp” với agency bên ngoài “năng suất tối đa”, theo sát agency, việc này tốn thời gian và chi phí của bộ phận marketing.
Tình hình Covid-19 hiện tại, công ty phải đối mặt với thách thức cắt giảm chi phí, vừa phải thay đổi phương án kinh doanh, sử dụng kênh bán hàng online là chủ yếu do lượng khách hàng đến cửa hàng đã giảm sút. Do đó công ty ngưng hợp tác với agency kia, và thuê 2-5 nhân viên chuyên về IT và Digital marketing (tập trung về SEO và website) để thay thế agency. Chính thức tự mình kiểm soát toàn bộ hoạt động trên web. Website được thay đổi hoàn toàn mới, và đã hoạt động được 6 tháng nay. Ban giám đốc muốn tìm hiểu liệu doanh thu ghi nhận từ các đơn đặt hàng trên website mới có khác biệt so với website cũ hay không. Nếu thấp hơn rõ rệt, công ty chắc phải thuê agency khác tốt hơn, còn ngược lại, nếu tăng công ty sẽ đầu tư mạnh hơn vào bộ phận Digital marketing và IT. Còn nếu không có sự khác biệt, công ty sẽ tiếp tục duy trì 2 bộ phận này, không đề xuất thêm các thay đổi cho đến khi Covid-19 tạm lắng xuống.
Một mẫu dữ liệu về doanh thu từ website bán hàng cũ được thu thập, lấy ngẫu nhiên 50 ngày, tương tự như sau khi triển khai website mới, cũng lấy doanh thu ngẫu nhiên 50 ngày.
Biết rằng độ lệch chuẩn tổng thể xác định được của trước khi có website mới và sau khi có website mới lần lượt là 3.8 triệu VND và 4 triệu VND. Giả sử mức ý nghĩa là 5%.
Chúng ta có bảng dữ liệu sau, đơn vị: triệu VND, mỗi mẫu chứa 50 quan sát
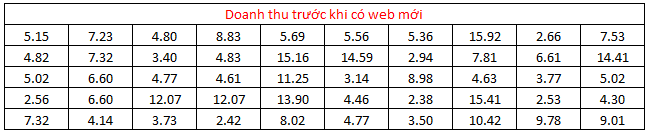
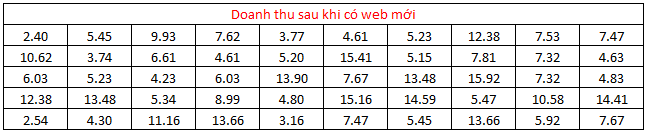
Lưu ý 2 mẫu này là độc lập, mẫu 1 là 50 ngày (quan sát) lấy ngẫu nhiên từ tổng các ngày khi triển khai web cũ, và mẫu 2 là 50 ngày (quan sát) lấy ngẫu nhiên từ 6 tháng gần đây sau khi triển khai web mới. Trung bình doanh thu tính được từ mỗi mẫu,
X1 = 6.95 triệu VND và X2 = 8.04 triệu VND
Do đầu tiên là kiểm định sự khác biệt nên chúng ta đặt giả thuyết như sau:
H0: µ1 – µ2 = 0
H1: µ1 – µ2 ≠ 0
µ1 và µ2 lần lượt là trung bình doanh thu 1 ngày khi áp dụng web cũ trong tổng thể, và khi áp dụng web mới trong tổng thể.
Đưa vào công thức kiểm định Z:
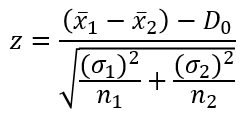
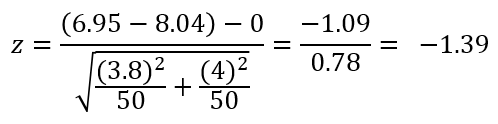
Chúng ta lấy trị tuyệt đối hoặc giữ nguyên kết quả z so với giá trị zα/2 với α = 0.05
Zα/2 = Z0.025 = 1.96
Như vậy Z = -1.39 > -Z0.025 = -1.96. nên theo quy tắc bác bỏ chúng ta không thể bác bỏ H0.
Tiếp theo p-value tính được = 2*(1 – 0.9177) = 0.16 lớn hơn α = 0.05. với 0.9177 là giá trị tra bảng tại trị tuyệt đối Z = 1.39. Các bạn xem lại bài viết trước để hiểu cách tính và cách tìm p-value sử dụng hàm excel. Link chúng tôi để ở phần đầu bài viết lần này.
Do đó kết luận không có sự khác biệt trong doanh thu trước và sau khi áp dụng web mới, tức khả năng doanh thu mà web mới đem lại sẽ không cao hơn so với web cũ, cũng như không thấp hơn. Như vậy công ty sẽ không đề xuất thêm các thay đổi cho đến khi Covid-19 tạm lắng xuống.
Trường hợp 2: độ lệch chuẩn của cả 2 tổng thể nghiên cứu chưa biết, và 2 mẫu độc lập, số quan sát ở mỗi mẫu < 30, hoặc ở một trong 2 mẫu < 30
Đối với trường hợp chúng ta không xác định được độ lệch chuẩn, phải sử dụng độ lệch chuẩn đã hiệu chỉnh của mẫu để thay thế, thì công thức kiểm định áp dụng sẽ là kiểm định t. Công thức như sau:
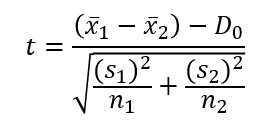
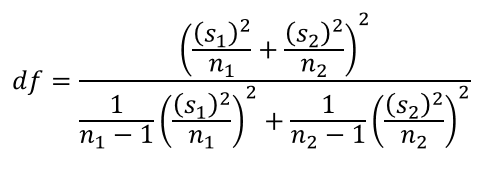
Điểm phức tạp ở đây là chúng ta phải tính được bậc tự do df (Degrees of freedom). Để hiểu bậc tự do là gì các bạn có thể xem trong bài blog của Minitab – công ty nổi tiếng chuyên về các giải pháp, phần mềm phân tích dữ liệu hàng đầu.
What Are Degrees of Freedom in Statistics?
Cách đặt giả thuyết thì cũng giống ở trên, về cách tra bảng t với bậc tự do df và cách tính p-value, và quy tắc bác bỏ cũng tương tự như kiểm định t trên một mẫu:
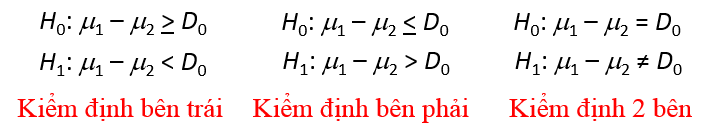
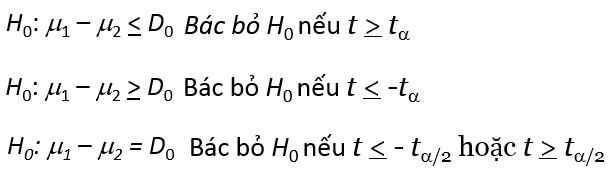
Chúng ta cùng đi qua một ví dụ khác.
Một công ty tại Hoa Kỳ đang phát triển một bộ các giải pháp phần mềm mới áp dụng nền tảng công nghệ hiện đại để giúp các chuyên viên IT thiết kế, xây dựng và triển khai hệ thống thông tin cho các công ty trong thời gian ngắn.
Để kiểm tra độ hiệu quả của nền tảng công nghệ mới, công ty chọn ngẫu nhiên 24 chuyên viên IT đến từ các công ty, lĩnh vực khác nhau, và phân ra làm 2 nhóm ngẫu nhiên, nhóm 1: 12 chuyên viên sẽ sử dụng bộ giải pháp hiện tại để xây dựng hệ thống thông tin, thời gian thực hiện của mỗi chuyên viên sẽ được thu thập. Nhóm 2: 12 chuyên viên còn lại sẽ sử dụng bộ gỉai pháp mới. Dữ liệu thu thập như sau:
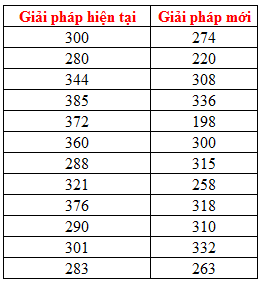
Như vậy nếu kết quả kiểm định cho thấy giải pháp mới tốt hơn thì sẽ chính thức đưa vào triển khai, còn ngược lại thì không. Vậy trung bình thời gian thực hiện của một chuyên viên IT khi sử dụng giải pháp mới sẽ phải thấp hơn giải pháp hiện tại.
Giả thuyết được đặt như sau:
H0: µ1 – µ2 ≤ 0
H1: µ1 – µ2 > 0
Giải pháp hiện tại: n1 = 12, trung bình x1 = 325 giờ, độ lệch chuẩn s1 = 40 giờ
Giải pháp mới n2 = 12, trung bình x2 = 286 giờ, độ lệch chuẩn s2 = 44 giờ
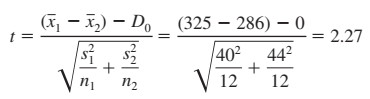
Bậc tự do theo công thức ở trên df = 21.8 làm tròn 22
t tra bảng với bậc tự do 22, mức ý nghĩa là 0.05 do kiểm định 1 phía: 1.717
t = 2.27 > t tra bảng. Vậy bác bỏ H0 tức giải pháp mới hiệu quả hơn giải pháp cũ
p-value tính được 0.017 nhỏ hơn mức ý nghĩa nên yên tâm bác bỏ H0.
Cách tính p-value cho kiểm định t 2 mẫu thực hiện giống như một mẫu. Các bạn có thể xem lại bài viết trước chúng tôi có trình bày rõ.
Lưu ý: nếu trường hợp cả 2 mẫu độc lập và cùng lớn hơn 30, nếu không biết độ lệch chuẩn của 2 tổng thể chưa biết, chúng ta có thể tính toán độ lệch chuẩn hiệu chỉnh của mẫu và thế vào công thức kiểm định Z thay vì kiểm định t. Nguyên nhân khi số quan sát trong mẫu lớn hơn 30, độ lệch chuẩn hiệu chỉnh của mẫu sẽ phù hợp để ước lượng cho độ lệch chuẩn của tổng thể.
Nhắc lại tại sao có con số 30 làm mốc điều kiện. Vì khi mẫu có số quan sát từ 30 trở lên, theo định lý giới hạn trung tâm (Central Limit Theorem), quy luật phân phối của trung bình mẫu sẽ xấp xỉ phân phối chuẩn – quy luật phân phối tổng thể tại giả thuyết H0, và công thức kiểm định Z sẽ được sử dụng. Còn ngược lại nhỏ hơn 30, quy luật phân phối của mẫu sẽ không được coi là xấp xỉ chuẩn, lúc này chúng ta phải sử dụng phân phối t-student, dạng phân phối giả định từ phân phối chuẩn áp dụng cho trường họp mẫu nhỏ và sử dụng kiểm định t.
Trường hợp 3: kiểm định 2 mẫu với trường hợp mẫu cặp
Như đã nói ở phần đầu bài viết về dạng kiểm định 2 mẫu chúng ta sẽ có dạng 2 mẫu độc lập, và mẫu cặp.
Đối với mẫu cặp, chúng ta có thể hiểu đơn giản, là số quan sát trong mẫu 1 và mẫu 2 là như nhau về lượng và chất. Ví dụ rõ hơn, trường hợp mẫu cặp thường được sử dụng để thử nghiệm các yếu tố tác động, thử nghiệm các giải pháp, sản phẩm,… trên cùng một nhóm các đối tượng, thường ứng dụng nhiều trong lĩnh vực kinh tế, xã hội.
Cách đặt giả thuyết:
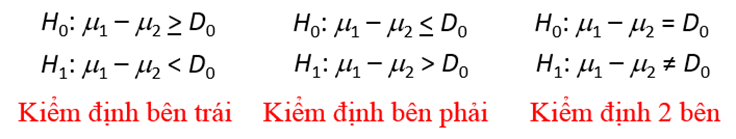
Ở một số tài liệu thống kê khác thường sử dụng µd để đặt giả thuyết với
µd = µ1 – µ2
Lý do tránh nhầm lẫn với trường hợp 2 mẫu độc lập.
Chúng ta cùng đi vào công thức kiểm định:
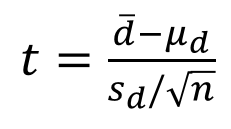
Với
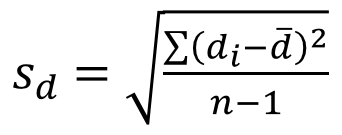
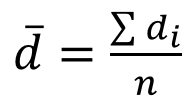
Phương pháp kiểm định 2 mẫu trường hợp mẫu cặp, hoàn toàn khác biệt với những dạng trên. Sử dụng giá trị chênh lệch.
Chúng ta sẽ tính giá trị chênh lệch của từng quan sát ở mẫu 1 và mẫu 2, sau đó tính giá trị trung bình tất cả các chênh lệch và tiến hành kiểm định trên giá trị ấy. Công thức sử dụng độ lệch chuẩn của các giá trị chênh lệch, theo như công thức ở trên. Nguyên tắc bác bỏ thì tương tự như kiểm định t thông thường.
Chúng ta cùng đi qua ví dụ các bạn sẽ dễ hiểu hơn:
Lý do các quán cà phê thường mở nhạc không phải chỉ để tạo không khí thoải mái, giúp khách hàng thưởng thức tốt hơn ly cà phê của mình và thu hút khách hàng quay trở lại, hay ở lại lâu hơn có thể mua thêm bánh ngọt, thức uống khác để thưởng thức tiếp. Nếu đối với các quán cà phê là những món nước thì đối với các nhà hàng sang trọng có thể là mùi hương tại quán. Mùi hương có thể giúp khách hàng thưởng thức món ăn ngon hơn, không khí dễ chịu, thư giãn giúp khách hàng ở lại lâu hơn, và có thể mua thêm những món ăn khác.
Còn đối với các công ty, liệu họ có thể tăng năng suất làm việc của nhân viên hay không nếu thay đổi môi trường làm việc thoải mái hơn cho nhân viên, giúp nhân viên thư giãn hơn?
Một công ty sản xuất khẩu trang tại thành phố Hồ Chí Minh đang nghiên cứu cách làm tăng năng suất của nhân viên sản xuất bên cạnh các chương trình khen thưởng thông thường, họ xây dựng chương trình radio âm nhạc cuối ngày làm việc cho nhân viên của mình, tức chương trình sẽ diễn ra từ 3 giờ đến 5 giờ chiều. Đồng thời công ty cũng làm thoáng không khí tại nơi sản xuất, yêu cầu nhân viên dọn dẹp, thêm các máy lọc không khí để giảm bớt những mùi khó chịu từ máy móc, nguyên vật liệu. Để kiểm chứng những thay đổi có làm tăng năng suất của nhân viên hay không, công ty thu thập dữ liệu năng suất nhân viên sản xuất trung bình 1 ngày của 20 nhân viên (chọn ngẫu nhiên để thử nghiệm) trước và sau khi áp dụng các thay đổi.
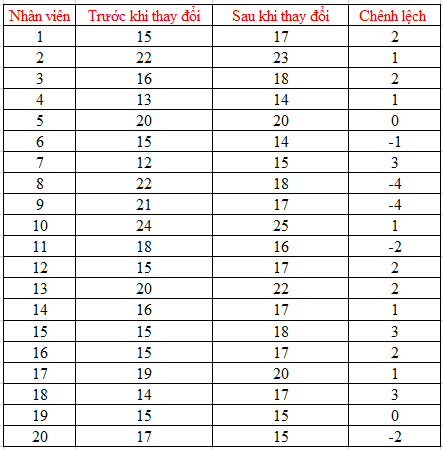
Đơn vị tính: hộp khẩu trang (thành phẩm), mỗi hộp có 50 khẩu trang, mức ý nghĩa 5%.
Đầu tiên chúng ta sẽ tính chênh lệch số hộp khẩu trang trung bình giữa trước và sau khi thay đổi của từng nhân viên.
Trung bình d tính được = 11/20 = 0.55, Sd = 2.139 (các bạn tính theo cách tính độ lệch chuẩn thông thường)
Đặt giả thuyết:
H0: µ1 – µ2 ≤ 0
H1: µ1 – µ2 > 0
Giá trị kiểm định t:
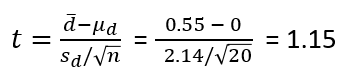
t tra bảng với bậc tự do n – 1 = 20 – 1 = 19, tại alpha = 0.05 (do kiểm định 1 bên) = 1.729
Như vậy t < t tra bảng nên không bác bỏ H0 tức sau khi áp dụng các thay đổi năng suất không những không tăng, có khả năng còn giảm. Công ty cần thu thập số liệu để phân tích thêm nếu kết quả vẫn bác bỏ, nghĩa là các phương án thay đổi có vấn đề nên tìm hiểu lại. Ví dụ có thể việc phát radio âm nhạc có thể khiến các nhân viên không tập trung, bàn luận về gu âm nhạc của lẫn nhau,…
P – value tính được là 0.1322 > 0.05 nên chúng ta không thể bác bỏ H0, nhắc lại cách tìm p-value ở kiểm định t các bạn có thể xem lại bài viết trước, link chúng tôi để ở phần đầu.
Lưu ý: khi mẫu lớn hơn 30, chúng ta sẽ sử dụng kiểm định Z với độ lệch chuẩn σd trong tổng thể đã biết hoặc thay thế Sd để tính
Dạng 2: kiểm định giả thuyết về sự khác biệt giữa 2 tỷ lệ tổng thể.
Dạng kiểm định này khá phức tạp ở cách tính và thông thường chỉ áp dụng cho trường hợp 2 mẫu độc lập. Chúng ta cùng tìm hiểu nhanh qua công thức:
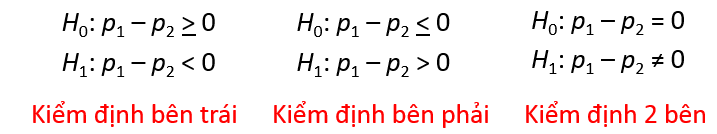
2 Mẫu dữ liệu được lấy ra ngẫu nhiên từ tổng thể phải lớn, thỏa mãn yêu cầu n1*p1, n2*p2, n1*(1 – p1) và n2*(1 – p2) phải lớn hơn hoặc bằng 5 (ở một số tài liệu thống kê khác có thể lớn hơn 5) thì lúc này mới đảm bảo phân phối xác suất cho tỷ lệ mẫu (p1 – p2) xấp xỉ phân phối chuẩn.
Công thức kiểm định Z như sau:
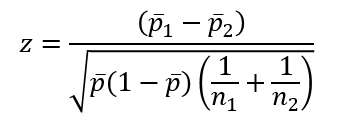
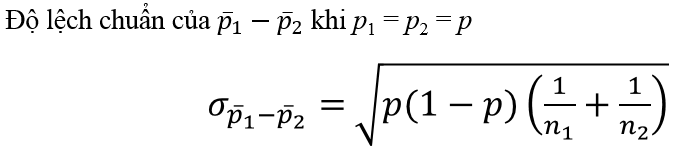
Trong trường hợp không xác định được p = p1 = p2 chúng ta sử dụng tỷ lệ p- dưới đây
Tỷ lệ p- là tỷ lệ các quan sát có tính chất nào đó chung trong 2 mẫu, là giá trị ước lượng của p khi p = p1 = p2, công thức như sau:
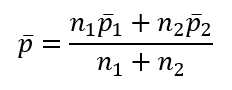
Lúc này độ lệch chuẩn S của mẫu được tính thay thế, có công thức sau:
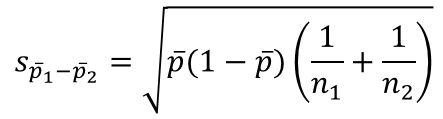
Quy tắc bác bỏ dựa trên giá trị kiểm định và p-value tương tự như các phương pháp kiểm định Z khác.
Chúng ta cùng đi qua ví dụ để hiểu hơn về dạng kiểm định này.
Ví dụ:

Một công ty sản xuất thiết bị điện tử gia dụng tại Hoa Kỳ tiến hành nghiên cứu độ hiệu quả của chiến dịch quảng cáo mới trên truyền hình và trên báo, tạp chí. Trước khi họ triển khai, dữ liệu thu thập cho thấy trong 150 hộ gia đình lấy ngẫu nhiên từ một thị trường thử nghiệm cho thấy có 60 hộ gia đình biết về các sản phẩm của công ty. Sau khi họ chạy các chiến dịch quảng cáo trong 1 tháng, dữ liệu thu thập từ 200 hộ gia đình thì có 96 hộ gia đình biết về sản phẩm của công ty.
Công ty sẽ thực hiện kiểm định tham số để đánh giá liệu chiến dịch quảng cáo mới có làm tăng tỷ lệ nhận biết của khách hàng hay không với mức ý nghĩa 5%
Chúng ta đặt giả thuyết:
H0: p1 – p2 < 0
H1: p1 – p2 > 0
Với p1 là tỷ lệ nhận biết sau khi đã triển khai chiến dịch mới xét trong tổng thể, p2 là trước khi triển khai.
Tỷ lệ mẫu p1 = 96/200 = 0.48
Tỷ lệ mẫu p2 = 60/150 = 0.4
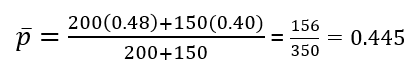
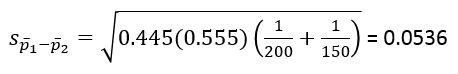
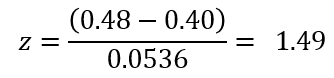
Tra bảng Zα với α = 0.05, Z0.05 = 1.645
Z < Z0.05 nên chúng ta không bác bỏ H0
p-value tính được = 0.0681 > α = 0.05 nên chắc chắn không thể bác bỏ H0.
Như vậy kết luận chiến dịch quảng cáo có thể không làm tăng độ nhận biết của khách hàng.
Đến đây là kết thúc chủ đề về kiểm định tham số dạng 1 mẫu và 2 mẫu. Đối với các dạng kiểm định phi tham số đặc biệt là ANOVA chúng tôi sẽ gửi đến các bạn ở dịp khác. Bài viết sắp tới chúng ta sẽ đi đến một mảng kiến thức rất phổ biến trong Data mining và được ứng dụng nhiều trong lĩnh vực kinh tế chính là Clustering với K-means Clustering.
Tài liệu tham khảo
“Statistics” của các tác giả James T. McClave, Terr y Sincich
“Essentials of Statistics for The Behavioral Sciences” của các tác giả Frederick J Gravetter, Larry B. Wallnau, Lori-Ann B. Forzano
“Basic statistics for business and economics” của các tác giả Douglas A. Lind, William G. Marchal, Samuel A. Wathen
“Statistics for Business and Economics” của các tác giả David R. Anderson, Dennis J. Sweeney, Thomas A. Williams và cộng sự
https://www.statisticshowto.com/probability-and-statistics/hypothesis-testing
hub.packtpub.com/how-data-scientists-test-hypotheses-and-probability/
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English