Trong các bài viết trước về tương quan (Correlation), hồi quy tuyến tính (Simple linear regression) đơn biến, BigDataUni và các bạn đã tìm hiểu về khái niệm, đặc điểm, cách phân biệt, cũng như cách triển khai các công thức của từng phương pháp trong việc đánh giá mối liên hệ giữa 2 biến phụ thuộc, biến độc lập. Chúng tôi cũng đã trình bày sơ lược về mô hình hồi quy tuyến tính đa biến (Multi linear regression), phương pháp đánh giá mối liên hệ giữa biến mục tiêu Y với nhiều biến đầu vào X. Ở bài viết lần này chúng ta sẽ đi vào ví dụ cụ thể, ứng dụng của mô hình hồi quy tuyến tính trong kinh doanh và bán lẻ.
Trong bối cảnh thay đổi liên tục, đặc biệt trong ngành bán lẻ, dữ liệu cần thu thập hàng ngày và phân tích là rất nhiều, do đó các kỹ thuật phân tích, khai phá dữ liệu được yêu cầu phải ngày càng tinh vi, có thể áp dụng linh hoạt, nhiều ưu điểm hơn. Đối với Regression cũng vậy, khi dữ liệu được cập nhật, đổi mới, các chuyên gia, những nhà nghiên cứu trong lĩnh vực khoa học dữ liệu sẽ quan tâm hay áp dụng nhiều các mô hình hồi quy chuyên sâu hơn, phù hợp hơn, thích ứng tốt với các thuộc tính, vấn đề mới của bộ dữ liệu. Điều này khiến cho phương pháp hồi quy tuyến tính – Linear regression không còn phổ biến, bị đánh giá là không còn thích hợp để áp dụng. Tuy nhiên, Linear regression vẫn là kiến thức nền tảng quan trọng nhất trong lĩnh vực thống kê và vẫn là công cụ phân tích đóng vai trò cốt lõi trong lĩnh vực kinh tế. Phương pháp hồi quy tuyến tính có ưu điểm đơn giản, dễ giải thích, thực hiện, diễn giải bằng đồ thị dựa vào phương trình hồi quy lập được, trực quan, rõ ràng, không cần phải nắm quá nhiều kiến thức nền tảng khác trong lĩnh vực khoa học dữ liệu để tiếp thu và triển khai. Bên cạnh đó Linear regression là công cụ đầu tiên, sơ khai, cơ bản nhất trong các công cụ phân tích được dùng để nghiên cứu nhanh chóng mối liên hệ giữa các yếu tố, đối tượng từ khoa học đến xã hội, mọi khía cạnh của đời sống và đưa ra những dự báo trong tương lai.
Đối với những ai đang tiếp cận Data science, hoặc Data mining, hay Data analytics chưa quen với các phương pháp xử lý dữ liệu thông thường, thì hồi quy tuyến tính có thể giúp hình thành những tư duy, am hiểu về dữ liệu, giúp nắm được bản chất của chính các công việc liên quan đến dữ liệu dễ dàng hơn, một phần giảm bớt các suy nghĩ nặng nề, chán nản khi khối lượng kiến thức phải tiếp thu là quá nhiều. Đặc biệt trong kinh tế, các nhà kinh doanh, thậm chí những nhân viên bán hàng, nhân viên marketing có thể sử dụng hồi quy tuyến tính để tự mình tìm ra câu trả lời cho các vấn đề, câu hỏi gặp phải hàng ngày dựa trên dữ liệu có sẵn. Bất kể phần mềm phân tích dữ liệu, trực quan dữ liệu, khai phá dữ liệu từ Excel, Minitab, SPSS, Rapid Miner, SAS,… cho đến ngôn ngữ lập trình xử lý dữ liệu như R, Python,… đều có tích hợp mô hình hồi quy tuyến tính cho phép chúng ta thực hiện và triển khai trên dữ liệu của mình.
Mặc dù thế giới đang thay đổi một cách chóng mặt, mọi hiện tượng, sự vật đều chuyển động không ngừng và luôn bị các yếu tố xung quanh tác động, dữ liệu vì thế phải cập nhật liên tục thì kết quả phân tích hồi quy tuyến tính không thể tuyệt đối tin tưởng và áp dụng vào thực tế, phải sử dụng thêm các phương pháp khác để đánh giá độ chính xác trong việc dự báo. Tuy nhiên không phải vì khuyết điểm rất lớn là không thể phản ánh đúng nhất các hiện tượng trong thực tế mà chúng ta bỏ qua hồi quy tuyến tính. Đây vẫn là phương pháp được khoa học công nhận, được tin tưởng, và luôn là kiến thức không thể thiếu ở những bộ môn về xử lý thông tin, dữ liệu tại hầu hết tất cả các trường đại học. Như theo tập đoàn công nghệ hàng đầu thế giới IBM “ Linear regression – A proven way to scientifically and reliably predict the future”. Cũng theo SAS, công ty hàng đầu khác về các phần mềm phân tích dữ liệu, Linear regression là phương pháp quan trọng nhất trong thống kê, giúp chúng ta tìm ra những thông tin có giá trị từ bộ dữ liệu lớn, về mối quan hệ giữa các đối tượng trong bộ dữ liệu và là công cụ không thể thiếu trong Predictive analytics – phân tích dự báo.
Dựa trên những lập luận trên, chúng ta có thể khẳng định hồi quy tuyến tính vẫn là công cụ hữu hiệu trong lĩnh vực kinh tế nói chung, và bán lẻ nói riêng trong việc tìm hiểu mối quan hệ giữa các yêu tố nghiên cứu quan trọng như giá cả, doanh thu, chiến dịch marketing, chiến lược bán hàng,…và đưa ra các dự báo, giải pháp hợp lý. Tuy nhiên chúng ta cũng cần quan tâm nhiều hơn về các cách thức đánh giá độ hiệu quả của mô hình hồi quy đảm bảo tính tối ưu.
Nói một chút về lĩnh vực bán lẻ, thì ngày nay bán lẻ cùng với thương mại điện tử là 2 ngành kinh tế được coi là phát triển mạnh nhất trong thời gian vừa qua, nhờ vào sự phát triển của công nghệ. Đối với các công ty trong ngành này, minh chứng là các tập đoàn lớn như Amazon, Walmart đã từ lâu coi dữ liệu là tài sản, là nguồn sống của mình, phải tận dụng và khai thác triệt để mục đích: thấu hiểu khách hàng thông qua hành vi, cách thức giao dịch, đưa ra các sản phẩm dịch vụ cá nhân hóa nhắm chính xác đối tượng khách hàng, xây dựng hệ thống giá linh hoạt, tối ưu hoạt động logistics,…
Trở lại với hồi quy tuyến tính, thì trong bài viết trước, chúng ta đã làm quen với các công thức, các bước cần thực hiện khi triển khai Multi linear regression – hồi quy tuyến tính đa biến. Thông thường trong thực tế khi chúng ta muốn đưa ra dự báo về một đối tượng nghiên cứu, chúng ta phải xem xét đến rất nhiều yếu tố khác tác động lên nó cùng lúc không chỉ là một, vì thế hồi quy tuyến tính đa biến được ứng dụng nhiều hơn. Ở bài viết này chúng tôi sẽ chỉ tập trung vào ví dụ sử dụng multi linear regression trong bán lẻ, còn về simple linear regression – hồi quy đơn biến, chúng tôi đã trình bày đầy đủ ở những bài viết trước, các bạn có thể tham khảo thông qua link dưới đây:
Tổng quan về Regression (phân tích hồi quy)
Correlation (tương quan) & Simple linear regression (hồi quy tuyến tính đơn giản)
Phương pháp kiểm định trong tương quan và hồi quy tuyến tính đơn biến
Dự báo trong Simple linear regression và sơ lược về Multi linear regression (chèn link vô sau)
Ứng dụng của hồi quy tuyến tính trong ngành bán lẻ hay kinh doanh là rất nhiều tùy vào từng trường hợp khác nhau, những mục tiêu nghiên cứu khác nhau của các nhà phân tích, các thuộc tính dữ liệu khác nhau, tuy nhiên tổng quan thông thường có các ứng dụng chủ yếu:
- Khai phá thông tin hữu ích, giá trị của các đối tượng nghiên cứu (ví dụ tìm hiểu sự liên hệ giữa chiến dịch marketing và doanh số)
- Đưa ra dự báo trong tương lai (ví dụ dự báo doanh thu của một cửa hàng tại khu vực bất kỳ dựa trên các yếu tố tác động đã được tìm thấy)
- Tối ưu quá trình vận hành, hoạt động (ví dụ dựa trên kết quả dự báo doanh số, lập ra các kế hoạch triển khai hàng tồn kho, kế hoạch logistics)
- Hỗ trợ ra quyết định, chiến lược (ví dụ dựa trên mối quan hệ giữa chiến dịch marketing và doanh số để đánh giá hiệu quả chiến lược tiếp thị hiện tại, và cần làm gì để thay đổi)
Trước khi đi vào ví dụ cụ thể, chúng ta cùng review lại những kiến thức, công thức cần nắm trong hồi quy tuyến tính đa biến.
Hồi quy tuyến tính đa biến là phương pháp nghiên cứu mối quan hệ giữa biến mục tiêu (biến phụ thuộc) với nhiều hơn 2 biến độc lập (biến đầu vào).
Mô hình tổng quan với Y là biến phụ thuộc và những biến độc lập X1, X2, X3,…,Xp.
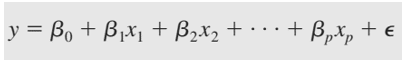
Giống như mô hình tổng quan của hồi quy tuyến tính đơn giản, β0 là giá trị ước lượng của Y khi các giá trị của các biến X đều bằng 0. Các hệ số hồi quy chưa biết từ β1… βp giờ đây sẽ được gọi là hệ số hồi quy riêng thể hiện mức độ thay đổi của giá trị trung bình Y khi biến X1…Xp thay đổi 1 đơn vị mà các biến còn lại không thay đổi. Tức là βp thể hiện mối liên hệ của riêng biến Xp đến giá trị trung bình của y. ε là sai số có phân phối chuẩn, trung bình bằng 0, là phần giá trị thể hiện các yếu tố mà mô hình không nghiên cứu đến.
Bên trên cũng chính là phương trình tổng quan hồi quy tuyến tính đa biến. Trong thực tế các hệ số hồi quy trong tổng thể không để tìm ra chính xác nên chúng ta chỉ có thể ước lượng bằng các hệ số b0, b1,..bp tính được từ dữ liệu mẫu. Phương trình hồi quy đa biến được dùng cho ước lượng, dự báo giá trị y

Y^ là các giá trị dự báo của biến mục tiêu, b0,…bp là các giá trị ước lượng của các hệ số β0,…,βp. Mặc dù cùng sử dụng phương pháp bình phương bé nhất (Least square method) nhưng điểm khác biệt giữa hồi quy tuyến tính đơn giản và hồi quy đa biến đó chính là quá trình tính toán. Với bộ dữ liệu mẫu nhỏ và chỉ có 2 biến, thì hồi quy tuyến tính đơn giản quá trình tính toán nhanh, có thể thực hiện bằng Excel lập bảng và sử dụng hàm để tính nếu số quan sát không quá lớn. Tuy nhiên với hồi quy đa biến công việc tính toán phức tạp hơn rất nhiều vì có rất nhiều biến, chưa kể tính tới số lượng quan sát trong tập dữ liệu.
Mô hình hồi quy đơn biến và đa biến đều dựa trên phương pháp bình phương bé nhất để hình thành phương trình và chỉ khác biệt về thời gian, chi phí tính toán, một bên 2 biến đơn giản hơn, một bên nhiều biến phức tạp hơn. Do áp dụng phương pháp bình phương bé nhất cùng với công thức ma trận đại số (Matrix Algebra) và không có các công thức toán nào khác có thể giúp mình tự tính toán (tính tay) đối với những dữ liệu đó nên thông thường khi tiến hành lập phương trình cho mô hình hồi quy đa biến chúng ta sẽ sử dụng các công cụ, phần mềm để phân tích và dựa vào kết quả để diễn giải mô hình. Đây là phần quan trọng nhất, nếu không hiểu các hệ số hồi quy diễn tả cái gì chúng ta sẽ khó đánh giá độ hiệu quả mô hình và đưa ra dự báo
Các công thức quan trọng bên cạnh việc diễn giải phương trình hồi quy đa biến
Các bạn có thể xem lại bài viết theo link dưới đây để hiểu hơn về ý nghĩa của từng công thức.
Dự báo trong Simple linear regression và sơ lược về Multi linear regression (chèn link vô sau)
- Correlation matrix để tìm hiểu mối quan hệ giữa tất cả các biến một cách tổng quan xem trước biến nào có thể sẽ có ích cho mô hình và ngược lại, dựa trên hệ số tương quan Pearson của từng cặp biến và ngăn chặn vấn đề đa cộng tuyến (Multicolinearity, các biến độc lập có tương quan với nhau ảnh hưởng đến kết quả dự báo Y không chính xác). Multicolinearity sẽ được chúng tôi trình bày rõ hơn ở bài viết tới.
- Hệ số xác định r2
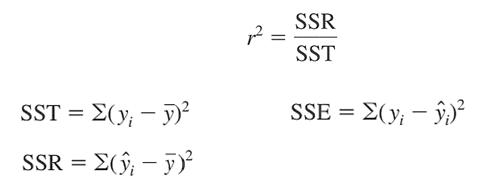
- Hệ số xác định R2 đã được hiệu chỉnh hay còn gọi là (Adjusted Coefficient of Determination)

- Công thức ước lượng hệ số hồi quy
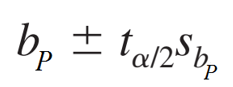
t tra bảng với bậc tự do là n-p-1, n là tổng số quan sát, p là số biến trong phương trình

- Công thức kiểm định F (kiểm định có hay không mối liên hệ giữa Y và một trong các biến X
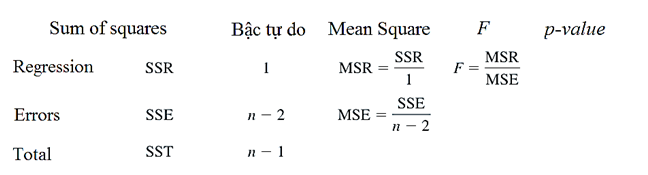
Nguyên tắc bác bỏ:
- p – value nhỏ hơn mức ý nghĩa α (có thể sử dụng bảng tra hay Excel để tìm ra dựa trên bậc tự do của F như dưới đây)
- Giá trị F tính được phải lớn hơn giá trị F tra bảng phân phối F (với bậc tự do thứ nhất là p ở hàng trên cùng, và bậc tự do thứ hai là n – p – 1 ở cột ngoài cùng, α ở cột thứ 2 tính từ cột ngoài cùng)
- Công thức kiểm định t (kiểm định mối quan hệ theo từng cặp biến X và Y)
Chúng ta có thể đặt các giả thuyết như sau, tùy theo mục đích kiểm định:
H0: βp = 0 H0: βp ≤ 0 H0: βp ≥ 0
H1: βp ≠ 0 H1: βp > 0 H1: βp < 0
Công thức tổng quát của giá trị kiểm định t như sau:
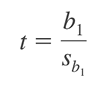
Nguyên tắc bác bỏ H0:
- Với kiểm định 2 phía: H0: βp = 0 được bác bỏ khi trị tuyệt đối của t lớn hơn t tra bảng (tα/2, n-p-1)
- Với kiểm định bên phải: H0: βp ≤ 0 được bác bỏ khi giá trị t dương lớn hơn giá trị dương của t tra bảng (tα, n-p-1)
- Với kiểm định bên trái: H0: βp ≥ 0 được bác bỏ khi giá trị t < giá trị âm của t tra bảng (tα, n – p-1)
- Nếu xét trên giá trị p-value, bác bỏ H0 khi p-value < α. (p-value là mức ý nghĩa nhỏ nhất mà tại đó H0 bị bác bỏ).
Kiểm định t sẽ được dùng để xác định biến X có ý nghĩa trong việc giải thích sự thay đổi của biến Y hay không, (chứ không nên kết luận theo kiểu có hay không có mối quan hệ giữa biến phụ thuộc Y với biến X như trong simple linear regression)
- Công thức ước lượng, dự báo
Phương pháp ước lượng và dự báo trong hồi quy đa biến thì tương tự trong hồi quy đơn biến. Thứ nhất có thể thay giá trị của các biến độc lập X vào phương trình hồi quy đa biến ước lượng kiếm được (sau khi đã tìm được các giá trị ước lượng b0, b1,… để dự báo giá trị của Y. Đây là dạng ước lượng điểm, giá trị Y được dự báo hay ước lượng sẽ là trung bình của các giá trị Y với giá trị X cho trước.

Thứ 2, ước lượng giá trị Y theo khoảng tin cậy thì có 2 dạng:
- Confident interval: áp dụng cho ước lượng giá trị trung bình của Y khi có các giá trị X cho trước. Công thức tổng quát:

- Prediction interval: áp dụng cho dự báo một giá trị riêng của Y khi có các giá trị X cho trước. Công thức tổng quát:

Tương tự như khi lập phương trình hồi quy đa biến, chúng ta phải sử dụng phần mềm phân tích dữ liệu để ước lượng giá trị y trong hồi quy đa biến do khối lượng dữ liệu nhiều, các công thức ma trận cần được áp dụng, nên việc tính tay là rất cồng kềnh và phức tạp, hiện nay mọi phần mềm phân tích dữ liệu đều tính giùm chúng ta các khoảng ước lượng của giá trị dự báo y y ở cả 2 loại, Confident và Prediction.
Lưu ý quan trọng:
Ngoài ra bên cạnh các công thức trên, thì trong hồi quy tuyến tính đa biến chúng ta còn có thêm các phương pháp quan trọng khác như phân tích sai số giữa giá trị thực tế và giá trị dự báo dựa theo phương trình hồi quy tìm được – Residual analysis (áp dụng cho mọi loại phân tích hồi quy), ngoài ra phương pháp này còn được dùng để kiểm tra những giả định về sai số ε; phương pháp Stepwise để đánh giá xem biến độc lập X nào nên giữ lại trong mô hình, và ma trận hệ số tương quan. Những phương pháp kể trên chúng tôi sẽ trình bày ở các bài viết sắp tới, đồng thời bàn luận sâu hơn về Multicolinearity – đa cộng tuyến.
Tiếp theo phần quan trọng nhất của bài viết đó là ứng dụng của hồi quy tuyến tính trong bán lẻ, cụ thể là ứng dụng mô hình Multi linear regression để tìm ra các thông tin hữu ích và có giá trị về mối quan hệ giữa các đối tượng nghiên cứu, mục đích đưa ra các dự báo và những chiến lược từ bán hàng, tiếp thị, vận hành, chuỗi cung ứng hiệu quả nhất.
Dự báo doanh thu dựa trên các yếu tố tác động là ứng dụng quan trọng nhất của hồi quy tuyến tính đa biến vì mục tiêu cốt lõi sau cùng của bất kỳ công ty bán lẻ nào cũng là doanh thu. Các yếu tố nào (các biến X) làm tăng giảm doanh thu (Y) trong tương lai? Tại sao? Cần làm gì để cải thiện hay hạn chế các yếu tố này.
Chủ đề về ứng dụng linear regression trong bán lẻ chúng tôi sẽ chia là 3 phần: phần thứ nhất thông qua một ví dụ đơn giản để hiểu những công thức liên quan, diễn giải ý nghĩa của kết quả phương trình hồi quy để nêu bật lợi ích của linear regression; phần thứ 2 sẽ trình bày về về các phương pháp chọn biến điển hình là Stepwise, phần thứ 3 sử dụng ví dụ khác để tổng hợp lại kiến thức và phương pháp đánh giá các giả định tham số ε thông qua Residual analysis như đã nói ở trên và bàn về các vấn đề có trong hồi quy đa biến ví dụ như Multicolinearity – đa cộng tuyến.
Phần 1 bài viết hôm nay ứng dụng linear regression trong bán lẻ, chúng ta sẽ bàn về ví dụ dự báo số tiền mà một khách hàng có thể bỏ ra ở lần mua hàng sắp tới. Số liệu và ví dụ lấy từ tài liệu quốc tế về thống kê và ứng dụng “The Basic Practice of Statistics” của David S.Moore.
Một quản lý tại một cửa hàng bán lẻ thời trang thu thập ngẫu nhiên dữ liệu lịch sử giao dịch của 60 khách hàng thân thiết, người quản lý này muốn dự báo ở lần mua hàng tiếp theo thì trung bình 1 khách hàng có thể sẽ bỏ ra bao nhiêu tiền để mua sản phẩm của cửa hàng. Nhiệm vụ của chúng ta là sẽ tìm ra mô hình hồi quy đa biến với các biến độc lập khác nhau để dự báo giá trị của biến mục tiêu là khoản tiền khách hàng bỏ ra. Các biến dữ liệu bao gồm:
- Amount (Target): Khoản tiền bỏ ra trong một lần giao dịch của một khách hàng tại cửa hàng bán lẻ. Đơn vị: USD
- Recency: số tháng kể từ lần cuối khách hàng mua hàng
- Frequency12: số lần mua hàng trong 12 tháng gần nhất
- Dollar12: tổng số tiền khách hàng đã bỏ ra để mua hàng trong 12 tháng gần nhất
- Frequency24: số lần mua hàng trong 24 tháng gần nhất
- Dollar24: tổng số tiền khách hàng đã bỏ ra để mua hàng trong 24 tháng gần nhất
- Card: đây là biến thay phiên, giá trị = 0 là khách hàng không có thẻ tín dụng, giá trị = 1 khách hàng có thẻ tín dụng
Lưu ý phương trình được tìm ra trong ví dụ dưới đây chưa được tối ưu nhất.
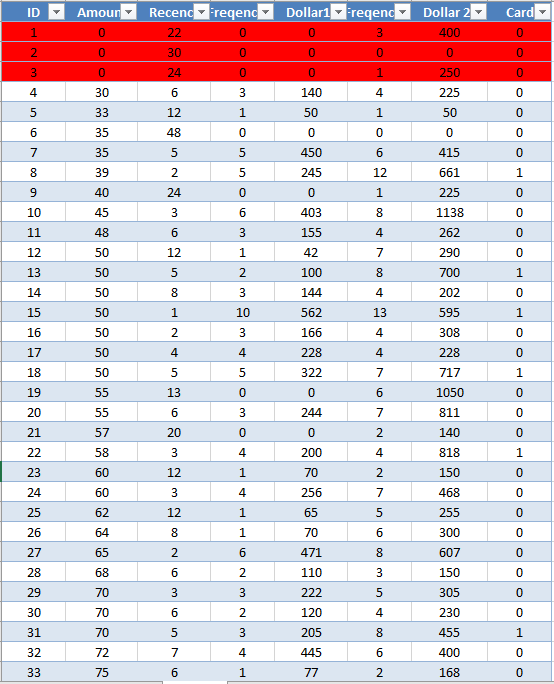

Đầu tiên chúng ta phải loại bỏ những dữ liệu ngoại lệ, tại cột biến Amount, 3 khách hàng đầu giá trị giao dịch bằng 0, trường hợp này có nghĩa là những khách hàng này đã mua hàng nhưng đã trả lại hàng, và cửa hàng phải trả lại tiền. Tại khách hàng thứ 60, giá trị giao dịch một là hơn 1 triệu USD, đây có thể là lỗi nhập thông tin, nên chúng ta cũng cần loại trừ ra.
Tiếp sau khi loại bỏ các dữ liệu ngoại lệ chúng ta sẽ lập ma trận hệ số tương quan để tìm mối liên hệ giữa biến mục tiêu. Các bạn có thể thực hiện trên Excel, SPSS để tìm ra ma trận.
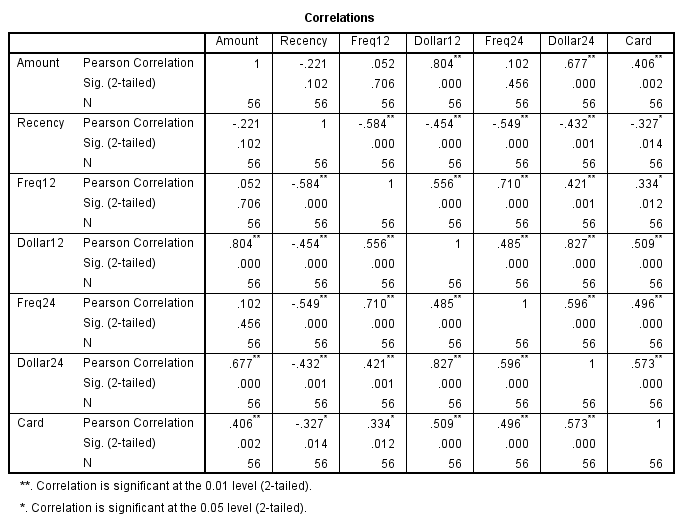
Dựa vào ma trận hệ số tương quan phía trên chúng ta xác định được 2 biến Dollar12 và Dollar 24 có mối quan hệ mạnh với biến mục tiêu là Amount, hệ số Pearson Correlation lần lượt là 0.804 và 0.677, tuy nhiên giữa 2 biến này lại có mối quan hệ bền vững với hệ số Pearson Correlation là 0.827, nên để tránh trường hợp đa cộng tuyến như đã nói ở trên chúng ta chỉ lấy một trong 2 biến Dollar12 và Dollar24 để đưa vào phân tích, chúng ta sẽ lấy Dollar12 vì hệ số Pearson cao hơn.
Biến Recency có ý nghĩa đưa vào phân tích vì nó là biến duy nhất có mối quan hệ ngược chiều khi hệ số tương quan với biến mục tiêu có giá trị âm nghĩa là những khách hàng nào mua hàng thường xuyên (Recency sẽ thấp, do số tháng từ lần cuối mua hàng sẽ giảm đi) sẽ có khả năng chi cao hơn khách hàng ít mua hàng (Recency cao, tức số tháng từ lần cuối mua hàng sẽ tăng lên). Biến Recency là biến có thể cung cấp thông tin hữu ích về khách hàng, chúng ta có thể xem xét đưa vào phân tích. Các giá trị Sig (2-tailed) là giá trị P-value, kết quả kiểm định hệ số tương quan để đánh giá có hay không có mối quan hệ giữa 2 biến, P-value càng bé, nhỏ hơn 0.005 thì chứng tỏ có mối quan hệ tương quan giữa 2 biến
Lưu ý cực kỳ quan trọng, ma trận hệ số tương quan chỉ cho chúng ta biết về mối quan hệ giữa các biến, biến độc lập nào có hệ số tương quan cao với biến mục tiêu có thể có ý nghĩa phân tích trong mô hình hồi quy đa biến nhưng biến độc lập nào có hệ số tương quan thấp hơn nghĩa là chúng không phù hợp để đưa vào mô hình, ngoài ra chúng ta phải xem xét thêm các hệ số R2 và R2 điều chỉnh hay sử dụng phương pháp Stepwise sẽ được chúng tôi trình bày ở bài viết tới. Ở bài viết lần này chúng ta sẽ đưa vô mô hình các biến mà chúng ta cho là quan trọng để phân tích, bên cạnh kết hợp với ma trận hệ số tương quan.
- Lưu ý phương trình dưới đây không phải là tối ưu nhất, nguyên nhân tại sao chúng tôi sẽ chỉ ra trong bài viết sắp tới cũng về linear regression trong bán lẻ, nhấn mạnh tầm quan trọng của phương pháp Stepwwise.
Giả sử sau khi xem xét chúng ta xác định được 3 biến độc lập X quan trọng cần đưa vào là Recency, Frequency12 và Dollar12. Như đã nói ở phía trên và bài viết trước, khi xây dựng mô hình hồi quy đa biến, chúng ta phải sử dụng các công thức ma trận để tính toán các hệ số hồi quy và khá cồng kềnh. Các phần mềm thống kê, phân tích dữ liệu hiện nay đều cho phép chúng ta tìm các hệ số hồi quy nhanh chóng và lập phương trình hồi quy đa biến dùng để ước lượng và dự báo giá trị biến mục tiêu:

Phía trên là kết quả có được từ SPSS, B chính là hệ số hồi quy của các biến, Standard Error là sai số chuẩn của hệ số hồi quy, chúng ta sẽ dùng hệ số này để ước lượng hệ số hồi quy theo khoảng tin cậy của từng biến X. Các bạn lưu ý giá trị p-value (cột Sig.) tại biến Recency, đây là nguyên nhân tại sao phương trình dưới đây không tối ưu hoàn toàn, trong bài viết thứ 2 chúng ta sẽ tìm hiểu, còn trước mắt chúng ta sẽ áp dụng và làm quen các công thức ước lượng, dự báo.
Chúng ta có phương trình hồi quy như sau:
![]()
Giải thích kết quả:
- 75 là giá trị ước lượng của Y khi các giá trị của tất cả các biến độc lập X đều bằng 0. Nghĩa là không xét đến các yếu tố liên quan khác, thì khoản tiền khách hàng bỏ ra một lần giao dịch có thể bằng 88.75 USD
- 44 là khoản tiền tăng thêm trong số tiền mua hàng khách hàng có thể bỏ ra lần tiếp theo khi tổng số tiền giao dịch trong 12 tháng gần nhất tăng 1 USD với điều kiện các biến lại được giữ nguyên không thay đổi.
- -1.1 là khoản tiền giảm đi trong số tiền mua hàng khách hàng có thể bỏ ra lần tiếp theo khi số tháng kể từ lần gần nhất khách hàng mua hàng tăng lên 1, cùng với điều kiện là các biến khác không thay đổi.
- -36.5 là khoản tiền giảm đi trong số tiền mua hàng khách hàng có thể bỏ ra lần tiếp theo khi tổng số lần mua hàng trong 12 tháng gần nhất tăng lên 1, cùng với điều kiện là các biến khác không thay đổi.
Tiếp theo chúng ta sẽ ước lượng hệ số hồi quy của từng biến. Lưu ý rằng các hệ số hồi quy trong phương trình trên là ước lượng điểm của hệ số hồi quy của các biến trong tổng thể và dĩ nhiên chúng sẽ không thể chính xác tuyệt đối. Quay lại công thức ước lượng hệ số hồi quy chúng tôi đề cập ở đầu bài viết, các bạn có thể áp dụng để tìm khoảng ước lượng cho từng hệ số hồi quy, với độ tin cậy 95%
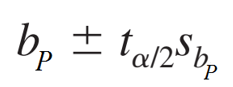
bp là hệ số hồi quy của từng biến có được từ phương trình, Sb là sai số chuẩn của hệ số hồi quy của chính biến đó, ta/2 là giá trị t tra bảng với α = 5%, bậc tự do n-p-1 = 56 – 3 -1 = 52, , Sb lấy từ kết quả ở trên
Chúng ta cùng ước lượng thử hệ số hồi quy của biến Dollar12.
T0.025, (52) = 2.007, Sb = 0.024.
Suy ra: 0.44 ± 2.007*0.024 => 0.44 ± 0.048 => hệ số hồi quy của Dollar12 nằm trong khoảng (0.39, 0.485)
Lưu ý quan trọng các bạn hãy nhìn lại kết quả ở trên, tại cột Lower 95% và Upper 95% đây là của Dollar12 các bạn sẽ thấy giống kết quả ước lượng như trên. Nghĩa là thay vì tính tay các bạn có thể lấy kết quả thông qua phần mềm phân tích.
Diễn giải: khi tổng số tiền giao dịch trong 12 tháng gần nhất tăng 1 USD thì số tiền giao dịch lần tiếp theo khách hàng bỏ ra sẽ tăng từ 0.39 USD đến 0.485 USD
Tiếp theo chúng ta cùng xem qua kết quả kiểm định F. Còn kiểm định t thì giống như hồi quy đơn biến chỉ khác cách thức kết luận nên các bạn có thể xem lại theo link bài viết dưới đây.
Phương pháp kiểm định trong tương quan và hồi quy tuyến tính đơn biến
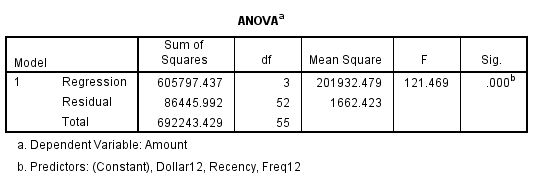
SSR = 605797.437 SSE = SST – SSR = 86445.992
SST = 692243.429
Bậc tự do của SSR là 3, là số biến độc lập trong phương trình. MSR = SSR/3 = 201932.479
Bậc tự do của SSE là n – p – 1 = 56 – 3 – 1 =52. MSE = SSE/52 = 1662.423
Chúng ta có giá trị kiểm định F = 121.469, các bạn có thể tra bảng phân phối F với bậc tự do thứ nhất là 3 và thứ 2 là 52 cùng α là 5%. Với giá trị F rất lớn và lớn hơn rất nhiều so với F tra bảng có giá trị khoảng 8.59, thì chứng tỏ một cách tổng thể là một trong các biến độc lập (recency, freq12, dollar12) đều có mối quan hệ với biến mục tiêu (amount). Lưu ý điểm này vì bài viết sắp tới chúng tôi sẽ nói lại ở bài viết sắp tới, điểm này rất rất quan trọng?
Tiếp theo là phần quan trọng nhất: liệu mô hình có ý nghĩa để đưa ra dự báo cho giá trị của biến Y, chúng ta sẽ xem xét hệ số điều chỉnh R2.
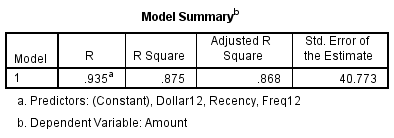
R2 = SSR/SST = 0.875
Nghĩa là 87.5% phần biến thiên trong giá trị của biến mục tiêu Y có thể được giải thích bởi các biến độc lập X. Nói cách khác 87.5% phần biến thiên trong khoản tiền khách hàng bỏ ra trong lần giao dịch sắp tới của khách hàng có thể được giải thích bởi số lần giao dịch trong 12 tháng gần nhất, số tháng kể từ lần giao dịch cuối cùng, và tổng số tiền giao dịch trong 12 tháng gần nhất. Hệ số R2 điều chỉnh 0.868 khá cao nên chúng ta có thể kết luận mô hình phù hợp để đưa ra dự báo.
Phương thức dự báo thứ nhất là chúng ta có thể thay trực tiếp các giá trị biến độc lập vào.
![]()
Giả sử người quản lý muốn dự báo số tiền trung bình một khách hàng có thể bỏ ra cho lần mua hàng tiếp theo nếu lần cuối khách hàng này mua hàng là 6 tháng trước, tổng số tiền khách hàng bỏ ra trong 12 tháng gần nhất là 200 USD, số lần mua hàng trong 12 tháng gần nhất là 2
Y = 88.75 + 0.44*200 – 1.1*6 – 36.5*2 = 97.15 USD.
Đối với 2 dạng ước lượng giá trị Y trong khoảng tin cậy là Confidental và Prediction Interval, chúng ta sẽ sử dụng SPSS để tìm ra kết quả ước lượng. Dưới đây là kết quả có được, lấy ví dụ 10 khách hàng.
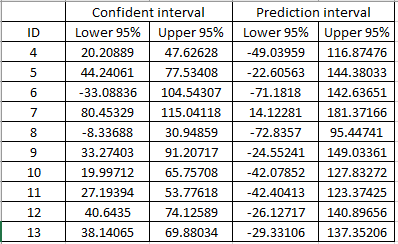
Diễn giải:
Chúng ta lấy ví dụ khách hàng ID 4, với Confidental interval cho giá trị Y dự báo (với giá trị của các biến đầu vào chúng ta lấy từ dữ liệu mẫu không thay đổi) là (20.2; 47.6), khoản tiền khách hàng bỏ ra trong lần mua hàng tiếp theo có thể nằm trong khoảng ước lượng trên. Còn Prediction interval (0; 116.87) (giá trị âm chúng ta loại bỏ vì nó không có ý nghĩa) là trường hợp khách hàng ID 4 là khách hàng mới với các giá trị của các biến độc lập giống như trong tập dữ liệu mẫu ban đầu.
Trong SPSS, giả sử nếu các bạn muốn dự báo khoản tiền của 1 khách hàng mới có thể bỏ ra cho lần giao dịch tiếp theo dựa trên cùng mô hình hồi quy thì các bạn có thể thêm các giá trị mới của các biến độc lập muốn dự báo lên trên cùng của sheet data, dòng đầu tiên phía dưới ngay các cột biến độc lập (cụ thể thêm giá trị ngay dòng 1), sau đó vào Analyze => linear => save => click “Unstandardized” tại phần Predicted values => click vào Mean, và Invidual tại Prediction interval => click continue thì sang sheet data bạn sẽ thấy 5 cột trong đó cột đầu tiên là giá trị dự báo của từng khách hàng kể cả khách hàng mới, các cột còn lại là kết quả ước lượng.
Các bạn có thể thấy đó, từ mô hình hồi quy tuyến tính chúng ta có thể dự báo được doanh thu của một cửa hàng bán lẻ dựa trên các dữ liệu giao dịch của khách hàng qua đó khẳng định lợi ích của phương pháp trong bán lẻ. Kết quả dự báo có chính xác hay không thì ở bài viết tới chúng tôi sẽ trình bày đến các bạn những phương pháp đánh giá mô hình hồi quy đa biến.
Tuy nhiên phương trình bên trên vẫn còn vấn đề mà các bạn chưa tìm ra, cụ thể như thế nào thì bài viết sắp tới chúng ta sẽ tìm hiểu ở phần 2 bài viết ứng dụng linear regression trong bán lẻ.
Như vậy đến đây là hết bài viết phần 1 về ứng dụng của lienar regression trong bán lẻ, mong các bạn tiếp tục ủng hộ chúng tôi trong các bài viết sắp tới.
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English