Ở bài viết trước chúng ta đã tìm hiểu về ứng dụng của hồi quy tuyến tính trong lĩnh vực bán lẻ với ví dụ đơn giản dự báo số tiền một khách hàng có thể bỏ ra cho lần mua hàng tiếp theo tại một cửa hàng thời trang. Chúng ta đã làm quen với cách diễn giải phương trình hồi quy đa biến – Multi linear regression, kết quả lấy được từ phần mềm thống kê SPSS, cũng đã xem được ma trận hệ số tương quan, đánh giá độ hiệu quả và ý nghĩa của mô hình thông qua kiểm định F, hệ số xác đinh R2, hệ số R2 điều chỉnh để xem mô hình có thích hợp để đưa ra dự báo hay không, từ đó thực hiện ước lượng hệ số hồi quy, ước lượng và dự báo giá trị của biến mục tiêu.
Tiếp nối phần 2, thông qua ví dụ bài viết trước về ứng dụng của hồi quy tuyến tính trong lĩnh vực bán lẻ, chúng ta sẽ đi qua tìm hiểu nguyên nhân tại sao phương trình hồi quy ở bài viết trước không hiệu quả bằng phương pháp Stepwise cùng với các phương pháp chọn biến độc lập x trong linear regression. Các bạn có thể xem lại bài viết trước bằng cách click vào link dưới đây:
Phương pháp kiểm định trong tương quan và hồi quy tuyến tính đơn biến
Correlation (tương quan) & simple linear regression (hồi quy tuyến tính đơn giản)
Dự báo trong linear regression & sơ lược về multi-linear regression
Hiểu hơn về Linear regression thông qua ví dụ ứng dụng trong bán lẻ (p.1)
Phương pháp chọn biến trong hồi quy tuyến tính (Variable selection procedures)
Bên cạnh kiểm định t, kiểm định t dùng để đánh giá mối liên hệ giữa từng biến x và y, được tính bằng công thức t = b/Sb với b và Sb của mỗi biến x, chúng ta còn có phương pháp khác.
Đối với mô hình hồi quy tuyến tính đa biến, đặc biệt trong trường hợp chúng ta phải phân tích một lúc nhiều biến độc lập và một biến phụ thuộc (biến mục tiêu). Câu hỏi đặt ra là có nhất thiết một mô hình hồi quy phải chứa tất cả các biến, hay còn gọi là các thuộc tính trong bộ dữ liệu hay không? Làm thể nào để chọn được những biến có ý nghĩa phân tích và loại bỏ những biến nào thừa, không có ý nghĩa phân tích ra ngoài mô hình. Chúng ta cần quan tâm: lựa chọn các biến độc lập x phù hợp khi đang xây dựng phương trình hồi quy, hay loại bỏ những biến độc lập x không có ý nghĩa phân tích. Phương pháp là đều dựa trên yếu tố kiểm định F và hệ số xác định R2 hay hệ số R2 điều chỉnh. Ví dụ chúng ta đang xây dựng mô hình với 2 biến x1, x2 và muốn kiểm tra nếu mô hình chỉ có một biến x1 thì có nhiều ý nghĩa thống kê (statistically significance) hơn mô hình 2 biến hay không? Nói cách khác, nếu chúng ta muốn bỏ mất 1 biến thì nên bỏ biến nào? Đối với kiểm định F, chúng ta có công thức tổng quát:
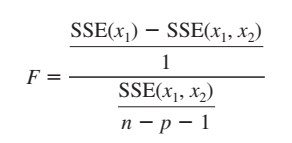
Giả thuyết chúng ta sẽ đặt là:
H0: β2 = 0
H1: β2 ≠ 0
Nghĩa là nếu hệ số hồi quy của biến x2 bằng 0 thì không có mối liên hệ tuyến tính giữa biến x2 và biến mục tiêu y, và ngược lại. Nếu F > F tra bảng với bậc tự do thứ nhất là 1 ở hàng trên cùng, và bậc tự do thứ hai là n – p – 1 ở cột ngoài cùng, α ở cột thứ 2 tính từ cột ngoài cùng. Giá trị 1 là số biến của mô hình đã được giảm biến hay là bậc tự do của SSR, nhớ lại công thức F tổng quát là MSR/MSE. MSR = SSR/p, ở đây SSR chênh lệch giữa 2 mô hình = SSE (x1) – SSE (x1, x2); MSE = SSE / (n – p – 1). Giá trị kiểm định F sẽ cho thấy biến x2 có làm giảm sai số của mô hình hay không, và ngoài ra p-value cũng là cơ sở để bác bỏ giả thuyết và xác định có giữ hay loại bỏ x2 hay không. Nếu p-value < α, thì biến có ý nghĩa phân tích, cần giữ lại trong mô hình, và ngược lại. Những bạn nào chưa biết về kiểm định là gì hay p-value là gì có thể xem lại bài viết thống kê suy luận của chúng tôi trong link dưới đây:
Tổng quan về statistics: inferential statistics (thống kê suy luận)
Tổng quát hơn, khi loại bỏ hay giữ lại các biến độc lập x chúng ta sẽ xem xét trước tiên liệu có mối quan hệ giữa các biến bị loại bỏ so với biến mục tiêu được hay không, tiếp theo là giữa mô hình mới đã loại bỏ biến và mô hình ban đầu, mô hình nào có sai số dự báo thấp hơn.
SSE (mô hình giảm biến) = SST – SSR (mô hình giảm biến)
SSE (mô hình ban đầu) = SST – SSR (mô hình ban đầu)
SSE (mô hình giảm biến) – SSE (mô hình ban đầu) = SSR (mô hình ban đầu) – SSR (mô hình giảm biến).
F = [SSE (mô hình giảm biến) – SSE (mô hình ban đầu)]/MSE (mô hình ban đầu). Chúng ta có thể linh hoạt sử dụng SSR hay SSE để tính giá trị F.
Tiếp theo đối với hệ số xác định R2 hay hệ số R2 điều chỉnh. Nếu mô hình một biến x1 sau khi được thêm biến x2 vào có hệ số xác định R2 tăng so với ban đầu thì x2 sẽ chính thức có ý nghĩa cho mô hình hồi quy đa biến và mô hình có ý nghĩa trong việc dự báo, xét tương tự cho x3, x4,… Cơ sở xem xét đó chính là nếu biến thêm vô mô hình mà không làm hệ số xác định R2 tăng thì không có ý nghĩa để đưa vào mô hình. Nhắc lại, hệ số R2 thể hiện phần biến thiên của biến Y có thể giải thích bởi các biến độc lập X, R2 càng cao thì mô hình càng có ý nghĩa trong việc dự báo giá trị Y. Hệ số điều chỉnh R2 được dùng để loại bỏ vấn đề khi thêm nhiều biến đầu vào đưa vào mô hình sẽ làm tăng hệ số R2, khiến hệ số R2 không còn hiệu quả trong việc đánh giá mô hình.
Lưu ý những phương pháp trình bày trong phần này chỉ áp dụng cho phân tích hồi quy, không giống với những phương pháp trong Feature Selection – lựa chọn biến phù hợp đưa vào phân tích trong các phương pháp khai phá dữ liệu trong Data mining.
Chúng ta có 4 cách chọn biến để đưa vào mô hình: Stepwise Regression, Forward Selection, Backward Elimination, và Best-subsets regression. Ở 3 cách đầu tiên, chúng ta sẽ kiểm tra mô hình theo từng bước, mỗi bước xem xét một biến và đưa biến nó vào mô hình, nếu biến này không phù hợp, thì chuyển sang biến khác, nếu biến đó phù hợp thì giữ lại trong mô hình, và dùng tiếp mô hình này để xét tiếp biến khác. Trong bài viết này, với ví dụ chỉ có 6 biến độc lập x, chúng ta sẽ chỉ tìm hiểu qua Stepwise Regression, đây là phương pháp phổ biến nhất và được tích hợp trong hầu hết các phần mềm phân tích dữ liệu.
Stepwise Regression
Stepwise regression là quá trình xem xét từng biến độc lập x khi thêm vào mô hình. Đầu tiên là tính giá trị kiểm định F và p-value cho lần lượt từng biến x để xem có loại biến đó hay không. Nếu biến này có ý nghĩa phân tích và được thêm vào, chúng ta có phương trình hồi quy tuyến tính. Tiếp theo bỏ thêm một biến x khác vào phương trình này, và tính lại giá trị kiểm định F hay p – values cho từng biến, nếu các biến đều có ý nghĩa phân tích chúng ta sẽ tiếp tục giữ trong mô hình, còn không thì loại biến không phù hợp và xét tiếp đến biến thứ 3, làm tương tự cho đến khi hết biến để thêm vào hay loại bỏ.
Bên cạnh kiểm định F hay p – values, chúng ta có thể sử dụng hệ số xác định R2, hay hệ số điều chỉnh R2 để xét cho từng biến thêm vào hay loại bỏ, bắt đầu từ mô hình 1 biến, và thêm lần lượt từng biến, kiểm tra mỗi mô hình, nếu hệ số không tăng tức biến không có ý nghĩa khi thêm vào mô hình. Đây sẽ là phương pháp chúng tôi sẽ dùng cho ví dụ trong bài viết này.
Lưu ý quan trọng không chỉ trong phương pháp Stepwise mà cả các phương pháp áp dụng để đánh giá ý nghĩa của các biến độc lập trong mô hình, đó là tại mỗi bước xem xét, chúng ta phải xem xét đầu tiên là xác định có biến nào cần loại bỏ hay không dựa vào kiểm định F, p-value hay R2. Nếu không có biến nào bị loại bỏ, thì chúng ta sẽ xét tiếp những biến nào chưa có trong phương trình và thêm vào. Nguyên nhân, khi một biến được thêm vào mô hình trước đó, thì lúc sau khi biến khác đưa vô mô hình, thì biến này có thể bị loại bỏ, và lần tới có thể lại được thêm vào, lần sau lại có thể bị loại bỏ. Stepwise kết thúc khi không còn biến thêm vào, hay loại bỏ.
Quay trở lại ví dụ bài viết trước ứng dụng hồi quy tuyến tính trong bán lẻ phần 1, ví dụ lấy từ tài liệu quốc tế về thống kê và ứng dụng “The Basic Practice of Statistics” của David S.Moore. Một quản lý tại một cửa hàng bán lẻ thời trang thu thập ngẫu nhiên dữ liệu lịch sử giao dịch của 60 khách hàng thân thiết, người quản lý này muốn dự báo ở lần mua hàng tiếp theo thì trung bình 1 khách hàng có thể sẽ bỏ ra bao nhiêu tiền để mua sản phẩm của cửa hàng bán lẻ. Nhiệm vụ của chúng ta là sẽ tìm ra mô hình hồi quy đa biến với các biến độc lập khác nhau để dự báo giá trị của biến mục tiêu là khoản tiền khách hàng bỏ ra cho cửa hàng bán lẻ này. Các biến dữ liệu bao gồm:
- Amount (Target): Khoản tiền bỏ ra trong một lần giao dịch của một khách hàng tại cửa hàng bán lẻ. Đơn vị: USD
- Recency: số tháng kể từ lần cuối khách hàng mua hàng tại cửa hàng bán lẻ
- Frequency12: số lần mua hàng trong 12 tháng gần nhất
- Dollar12: tổng số tiền khách hàng đã bỏ ra để mua hàng trong 12 tháng gần nhất
- Frequency24: số lần mua hàng trong 24 tháng gần nhất
- Dollar24: tổng số tiền khách hàng đã bỏ ra để mua hàng trong 24 tháng gần nhất
- Card: đây là biến thay phiên, giá trị = 0 là khách hàng không có thẻ tín dụng, giá trị = 1 khách hàng có thẻ tín dụng
Dữ liệu sau khi đã loại bỏ các đối tượng có giá trị ngoại lệ:
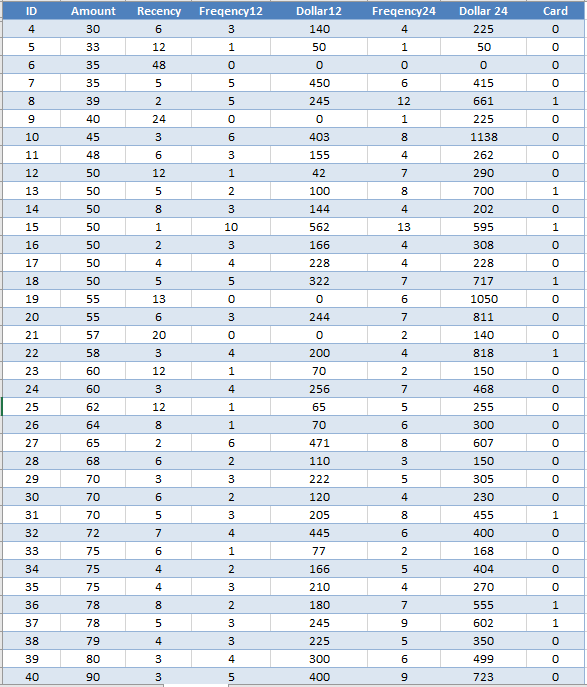
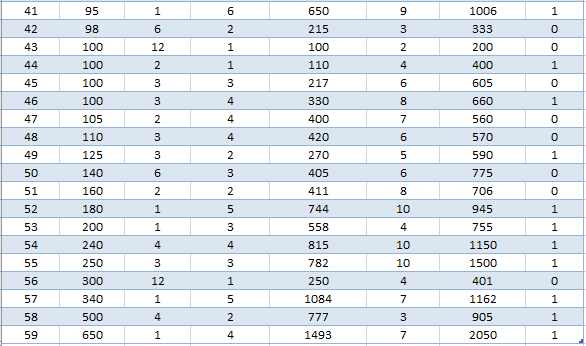
Bài viết trước chúng tôi đã cung cấp cho các bạn phương trình hồi quy đa biến dự báo số tiền khách hàng bỏ ra cho một lần mua hàng tại cửa hàng bán lẻ thời trang:
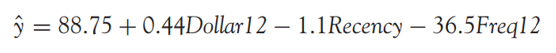
Nhưng phương trình hồi quy trên liệu có hoàn toàn phù hợp? chúng ta sẽ xem xét bằng cách áp dụng phương pháp Stepwise kết hợp kiểm định F, p-value hay R2 như đã nói ở trên. Để nhanh chóng chúng ta sẽ sử dụng SPSS để lấy kết quả trực tiếp từ phương pháp Stepwise. Nguyên nhân là phương pháp Stepwise có rất nhiều bước dựa vào số biến độc lập x, nên chúng tôi không thể trình bày hết sẽ làm dài bài viết. Trong thực tế cũng ít ai tự mình thực hiện từng bước trong Stepwise, đặc biệt khi bộ dữ liệu ngày nay rất nhiều biến và phức tạp.
Chúng ta sẽ sử dụng phương pháp Stepwise để chọn ra những biến phù hợp và lập phương trình hồi quy cho ví dụ ứng dụng trong bán lẻ này. Các bạn có thể sử dụng các phần mềm thống kê khác nhau để thực hiện, trong bài viết này chúng tôi sẽ triển khai Stepwise thông qua SPSS. Đây là kết quả chúng ta có được.
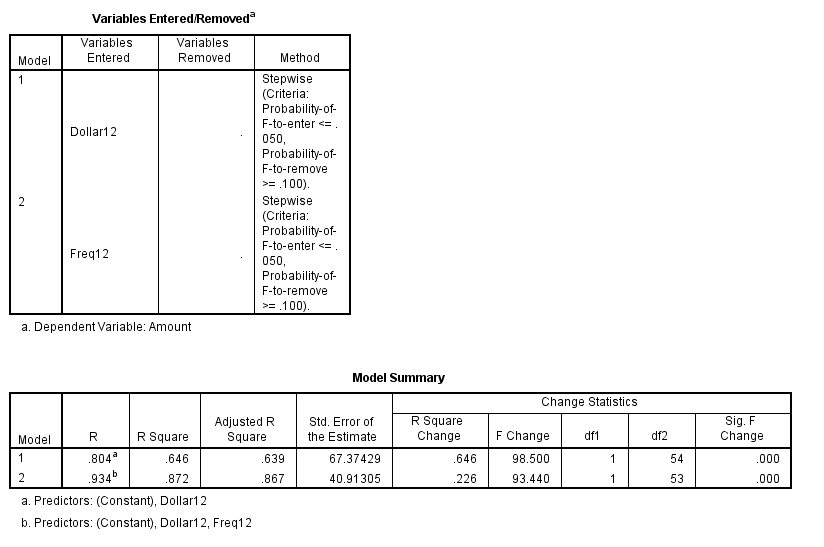
Sau khi đã xét hết các biến thì SPSS cho rằng phù hợp nhất cho mô hình sẽ là 2 biến Dollar12 và Freq12 – số lần khách hàng giao dịch trong 12 tháng. Mô hình thứ nhất với 1 biến Dollar12, (Constant là giá trị b0, nên chúng ta không tính là một biến, hãy nhớ lại phương trình hồi quy tổng quát trong bài viết trước) có giá trị kiểm đinh F rất lớn và lớn hơn giá trị F tra bảng với α = 0.05, tương tự như mô hình thứ 2 nên để đánh giá biến Freq12 khi thêm vào mô hình nó có ý nghĩa hay không chúng ta phải xem qua hệ số R2. Nhận thấy tại cột R-square, hệ số có tăng tự 0.639 đến 0.872, tương tự như hệ số R2 điều chỉnh nằm ở cột Adjusted R-square cũng tăng. Ngoài ra sai số dự báo của mô hình thứ 2 giảm mạnh so với mô hình thứ nhất. Qua đó chúng ta có thể khẳng định biến Freq12 thích hợp cho mô hình hồi quy. Lưu ý hệ số α để xét cho p-value là 0.05 khi p-value nhỏ hơn sẽ thêm biến vào mô hình, và là 0.1 khi p-value lớn hơn loại bỏ biến khỏi mô hình, mặc định trong SPSS, tuy nhiên các bạn vẫn có thể điều chỉnh. Với 2 giá trị kiểm định F quá lớn thì p-value chắc chắn sẽ nhỏ hơn 0.05, các bạn có thể biết được ngay nếu có kinh nghiệm kiểm định F thường xuyên. Giá trị tra bảng của F với alpha là 0.05 thường nhỏ dần khi bậc tự do phía cột bên trái, là số biến độc lập của mô hình tăng lên.
Nhớ lại bài viết trước ứng dụng linear regression trong bán lẻ phần 1, khi xem qua ma trận hệ số tương quan, chúng ta có thể thấy 2 biến có mối liên hệ mạnh nhất với biến mục tiêu có mối quan hệ mạnh nhất với biến Amount đó chính là Dollar12, Freq12. Qua đó khẳng định lần nữa kết quả từ phương pháp Stepwise có thể chính xác.
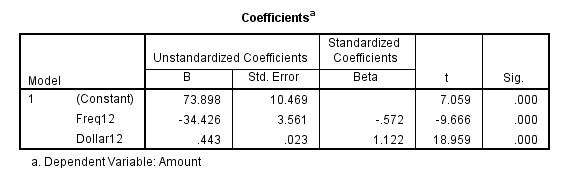
Như vậy sau khi thực hiện phương pháp Stepwise, chúng ta có mô hình hoàn hảo nhất:
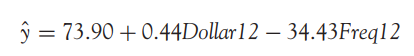
Diễn giải:
- 90 là giá trị ước lượng của Y khi các giá trị của tất cả các biến độc lập X đều bằng 0. Nghĩa là không xét đến các yếu tố liên quan khác, thì khoản tiền khách hàng bỏ ra một lần giao dịch tại cửa hàng bán lẻ có thể bằng 73.90 USD
- 44 là khoản tiền tăng thêm trong số tiền mua hàng khách hàng có thể bỏ ra lần tiếp theo khi tổng số tiền giao dịch trong 12 tháng gần nhất tăng 1 USD với điều kiện các biến lại được giữ nguyên không thay đổi.
- -34.43 là khoản tiền giảm đi trong số tiền mua hàng khách hàng có thể bỏ ra lần tiếp theo tại cửa hàng bán lẻ khi tổng số lần mua hàng trong 12 tháng gần nhất tăng lên 1, cùng với điều kiện là các biến khác không thay đổi.
Tuy nhiên với chỉ 6 biến độc lập x ban đầu mà chúng ta chỉ có thể lập mô hình có 2 biến thì đây có thể cũng chưa hoàn toàn hiệu quả, có thể bị Underfitting, mô hình chưa xét hết các yếu tố tác động lên kết quả dự báo, do những biến còn lại đôi khi có ý nghĩa phân tích, cũng có thể quan tâm. Ngoại trừ 2 biến Dollar24, Freq24, 2 biến có điểm chung là cung cấp thông tin về giao dịch của khách hàng trong 2 năm, trong thực tế thì 2 năm là khoảng thời gian quá dài, hành vi khách hàng có thể thay đổi hoàn toàn trong 2 năm mà chúng ta không thể kiểm soát. Vậy còn 2 biến Recency, Card thì sao? Chúng ta cùng xem qua nguyên nhân vì sao SPSS không thêm những biến còn lại vào mô hình bằng cách thêm lần lượt từng biến vào mô hình và xem xét các giá trị kiểm định F, p-value và hệ số R2. Phương pháp này có tên gọi khác với Stepwise, trong SPSS gọi đây là phương pháp “Enter” – thêm từng biến, chúng ta cũng có thể dựa vào phương pháp này để hiểu rõ hơn về kết quả mà Stepwise đem lại, tại sao mô hình mà Stepwise đưa ra là tối ưu nhất. Phương pháp thêm từng biến này thực chất cũng sử dụng những công thức kiểm định F, giá trị p-values, và hệ số R2, chỉ khác biệt là nó cho chúng ta thấy mô hình nào hiểu quả hơn, từ một biến đến 6 biến.
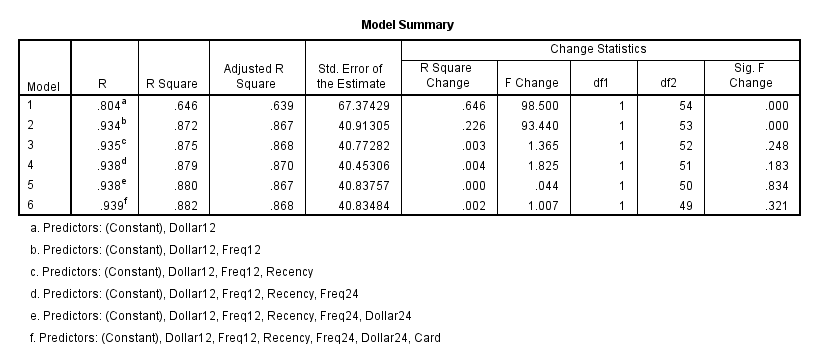
Nhìn vào kết quả chúng ta thấy được lý do tại sao chúng ta thấy được từ mô hình thứ 1 đến mô hình thứ 4, hệ số R2 và hệ số điều chỉnh R2 đều tăng, tuy nhiên tại mô hình 3 và 4, p-value (sig F change, giá trị kiểm định ở công thức đầu bài viết) lớn hơn 0.05, nghĩa là biến thêm vào mô hình thứ 2 (Recency) và biến thêm vào mô hình thứ 3 (Freq24) không phù hợp để đưa vào mô hình. Các bạn có thể thấy mô hình thứ 5, 6 cũng tương tự như vậy mà loại bảo. Mô hình thứ 1 và thứ 2 đều có p-value < 0.05, nhỏ hơn rất nhiều nên 2 mô hình này là phù hợp để phân tích, kết quả giống như Stepwise cung cấp.
Vì thế chúng ta không cần quan tâm nữa đến biến Dollar24, Freq24, và Card, như vậy chỉ còn biến Recency thì sao? Trong ma trận hệ số tương quan ở bài viết trước, Recency là biến duy nhất có hệ số tương quan âm với biến mục tiêu, nghĩa là Recency sẽ thấp, do số tháng từ lần cuối mua hàng sẽ giảm đi sẽ có khả năng chi cao hơn khách hàng ít mua hàng Recency cao, tức số tháng từ lần cuối mua hàng sẽ tăng lên, các khách hàng này có thể thích mua sắm ở những cửa hàng khác nhau, chứ không chỉ duy nhất cửa hàng mà chúng ta đang phân tích. Recency còn cho thấy hiệu quả kinh doanh, hiệu quả marketing, hiệu quả CRM của chính cửa hàng. Tuy nhiên chúng ta không thể đưa biến này vào mô hình vì p-value > 0.05 rất nhiều, và nguyên nhân thoe kết quả phân tích nó có thể nó không thể hiện tuyệt đối mối liên hệ bền vững với số tiền mà khách hàng có thể bỏ ra trong mỗi lần mua hàng. Do đó kết luận sau cùng, chúng ta sẽ loại bỏ biến Recency từ mô hình ở bài viết trước.
Có một ý mà chúng tôi muốn lưu ý lại trong bài viết trước về kiểm định F.
Quay trở lại với phương trình ở bài viết trước mà chúng ta cho rằng không tối ưu:
![]()
Chúng ta có kết quả kiểm định F từ bảng ANOVA:
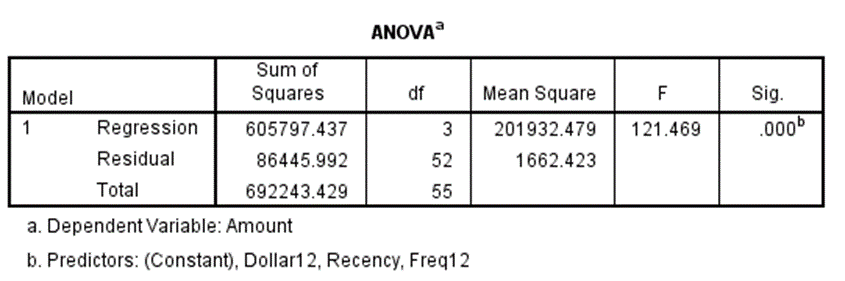
Chúng ta có giá trị kiểm định F = 121.469, các bạn có thể tra bảng phân phối F với bậc tự do thứ nhất là 3 và thứ 2 là 52 cùng α là 5%. Với giá trị F rất lớn và lớn hơn rất nhiều so với F tra bảng có giá trị khoảng 8.59, thì chứng tỏ một cách tổng thể là một trong các biến độc lập (recency, freq12, dollar12) đều có mối quan hệ với biến mục tiêu (amount). Các bạn đừng dựa vào giá trị p-value hay kiểm định F này cho rằng mô hình phù hợp để phân tích. Điều này hoàn toàn sai. Vì kiểm định F này chỉ cho biết biến mục tiêu có hay không có mối liên hệ với ít nhất một trong các biến độc lập x, nghĩa là nếu biến Amount có mối liên hệ ít nhất giữa một trong các biến Dollar12, Freq12, Recency, thì p-value sẽ nhỏ hơn 0.05. Như vậy nếu dựa vào đây, thì chúng ta sẽ bỏ sót biến Recency chưa tìm hiểu kỹ. Một điểm nữa cần lưu ý, p-value ở bảng trên cột (sig F change) hoàn toàn khác với giá trị p-value chúng ta vừa nói đến. Giá trị p-value tại Sig F change chính là giá trị kiểm đinh F trong công thức đầu tiên mà chúng tôi nói đến ở đầu bài viết.
Chúng ta cùng quay lại với công thức kiểm định F đầu tiên trong bài viết để xem liệu biến Freq12 có cần thiết để đưa vào mô hình phân tích hay không.
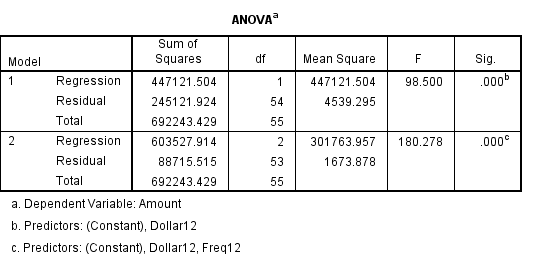
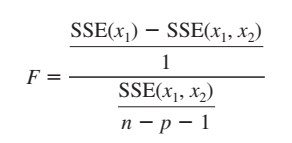
H0: β2 = 0
H1: β2 ≠ 0
Beta 2 chính là hệ số hồi quy của biến Freq12.
Chúng ta sẽ thay vào công thức: SSE(x1) = 245121.924, SSE(x1, x2) = 88715.515, n = 55, p = 2
F = [(245121.924 – 88715.515)/1] / [(88715.515)/53] = 93.439 đây chính là kết quả chúng ta có được từ Stepwise. Các bạn hãy quan sát cột F change dưới đây.
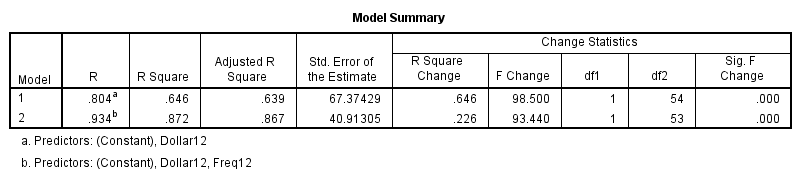
Giá trị tra bảng F với alpha = 0.05, bậc tự do bên cột trái là 2 là giá trị p, bậc tự do ở dòng trên là n = 55, giá trị F tra bảng = 8.57 < F = 93.440 như vậy kết luận bác bỏ H0, tức biến Freq12 có ý nghĩa trong mô hình. Lưu ý nữa giá trị kiểm định F của tổng thể mô hình thứ 2 là 180.278 không bằng giá trị kiểm điểm F của tổng thể mô hình thứ 1 cộng lại với F change vừa tìm.
Như vậy bài viết phần 2 ứng dụng hồi quy tuyến tính trong bán lẻ đến đây kết thúc, ở bài viết phần 3 chúng ta sẽ đi qua vấn đề đa cộng tuyến Multicolinearity sử dụng lại ví dụ của cửa hàng bán lẻ thời trang.
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English