Bigdatauni.com Follow Fanpage Contact
Quay trở lại với chủ đề bài viết về kiểm định phi tham số (Non-parametric test), ở bài viết phần 1 chúng ta đã tìm hiểu phương pháp kiểm định Chi bình phương (Chi-square test) ứng dụng để kiểm tra giả định về quy luật phân phối và kiểm tra mối quan hệ giữa 2 yếu tố, đặc điểm của các đối tượng nghiên cứu.
Tiếp tục với bài viết phần 2 kết thúc chủ đề kiểm đinh phi tham số, BigDataUni và các bạn cùng đi tiếp sang các công thức khác bao gồm Sign – test, Wilcoxon – rank test, Mann – Whitney test, Kruskal – Wallis test với các ứng dụng thực tế trong lĩnh vực kinh doanh.
Lưu ý, để hiểu về các phương pháp kiểm định phi tham số các bạn cần có kiến thức cơ bản liên quan đến thống kê, các bạn có thể tham khảo lý thuyết thống kê thông qua các bài viết của chúng tôi tại các link dưới đây:
Tổng quan về Statistics: Khái niệm và ứng dụng của thống kê
Tổng quan về Statistics: Descriptive statistics (thống kê mô tả)
Tổng quan về Statistics: Inferential statistics (thống kê suy luận)
Tìm hiểu về phương pháp kiểm định tham số
Các dạng kiểm định tham số (trường hợp 1 mẫu)
Các dạng kiểm định tham số (trường hợp 2 mẫu)
Kiểm định phi tham số (P.1): Kiểm định Chi Bình Phương

Sign – test
Kiểm định dấu hay còn gọi Sign – test là dạng kiểm định phi tham số đơn giản nhất áp dụng cho phân tích, kiểm tra các giả thuyết từ tập dữ liệu chứa các mẫu dữ liệu cặp, mẫu dữ liệu đôi, được ứng dụng nhiều trong lĩnh vực kinh tế, đặc biệt là Sales, và Marketing trong khảo sát một nhóm khách hàng để đánh giá trải nghiệm sản phẩm, dịch vụ, tìm hiểu khách hàng ưa thích sản phẩm, dịch vụ nào hơn, so sánh trong chính các sản phẩm của công ty, hay so sánh giữa các công ty đối thủ với nhau.
Kiểm định dấu là một phương pháp kiểm định phi tham số linh hoạt để kiểm tra giả thuyết sử dụng phân phối nhị thức (Binominal distribution) với p = 0.50, và không yêu cầu đưa ra bất kỳ giả định nào về quy luật phân phối.
BigDataUni cũng từng giới thiệu đến các bạn phương pháp kiểm định tham số cho giả thuyết nói về sự khác biệt giữa các đối tượng nghiên cứu nằm trong mẫu cặp (ví dụ: đánh giá năng suất của nhóm nhân viên trước (mẫu/ tổng thể 1) và sau (mẫu/ tổng thể 2) khi áp dụng phương pháp sản xuất mới) và mẫu độc lập (ví dụ so sánh sự khác biệt trong doanh thu giữa 2 sản phẩm A (mẫu/ tổng thể 1) và B (mẫu/ tổng thể 2) trong năm vừa rồi) yêu cầu đưa ra giả định là các tổng thể nghiên cứu tuân theo phân phối chuẩn, dữ liệu sử dụng là dữ liệu định lượng, công thức triển khai là công thức kiểm định t.
Sign – test được cho là linh hoạt khi nó có thể áp dụng cho cả dữ liệu định tính và cả dữ liệu định lượng, không yêu cầu tổng thể nghiên cứu phải theo phân phối chuẩn. Nào chúng ta cùng đi qua ví dụ cụ thể sau:
Một công ty thương mại điện tử vừa đưa vào triển khai hệ thống Chatbot AI tương tác với khách hàng tự động và 24/7, để kiểm tra liệu Chatbot có mang lại trải nghiệm khách hàng, có đáp ứng nhu cầu của khách hàng tốt hơn đội ngũ nhân viên CSKH hiện tại không? Công ty tiến hành khảo sát 20 khách hàng là khách hàng thân thiết của công ty 2 lần, lần 1 là trước khi ứng dụng Chatbot, 2 là sau khi ứng dụng Chatbot, dưới đây là kết quả thu được.
Hệ thống đánh giá theo 5 mức độ:
1 – Rất không hài lòng
2 – Không hài lòng
3 – Bình thường
4 – Khá hài lòng
5 – Rất hài lòng
Dấu thể hiện sự khác biệt giữa đánh giá của khách hàng trước khi ứng Chatbot AI (hệ thống CSKH hiện tại) và sau khi ứng dụng Chatbot AI, nếu đánh giá sau tốt hơn đánh giá trước chúng ta sẽ thêm dấu + và ngược lại là dấu trừ, giống nhau thì chúng ta sẽ để trống hoặc có thể thay bằng số 0.
Gọi là kiểm định dấu vì chúng ta sẽ sử dụng do chúng ta sẽ sử dụng chính các dấu (+) (-) vào công thức phân tích.
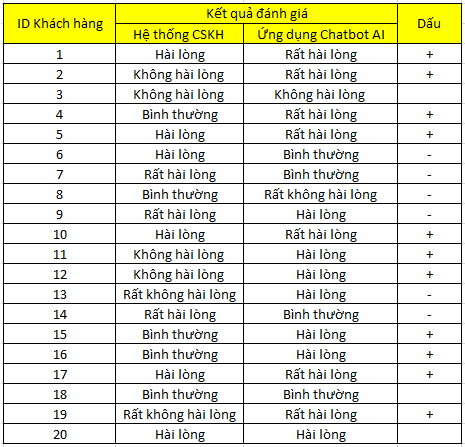
Như đã nói ở trên chúng ta sẽ sử dụng phân phối nhị thức với p = 0.5. Giải thích, p chính là xác suất để khách hàng đánh giá ứng dụng Chatbot AI tốt hơn hệ thống CSKH hiện tại.
Nếu p = 0.5, xác suất để khách hàng đánh giá Chatbot AI tốt hơn tức (+) và đánh giá Chatbot AI kém hiệu quả hơn tức (-) là như nhau, mỗi bên 0.5. Tức là để biết việc ứng dụng Chatbot AI có mang lại sự khác biệt hay không chúng ta cần khách hàng đánh giá tốt, hoặc xấu, nếu bình thường, không có ý kiến hoặc đánh giá tương đương với hệ thống CSKH, chúng ta sẽ loại bỏ không xét đến.
Tiếp tục, các bạn hiểu đơn giản như sau, nếu kết quả khách hàng đánh giá ứng dụng Chatbot AI thu thập mà trong đó số dấu (+) và (-) ngang nhau thì nghĩa là ứng dụng Chatbot AI cũng không tốt hơn cũng không xấu hơn so với hệ thống CSKH.
Do đó gọi P là tỷ lệ khách hàng đánh giá Chatbot AI tốt hơn xét trong tổng thể nghiên cứu (trong thực tế). Như vậy chúng ta đặt giả thuyết như sau:
H0: p = P =0.5
H1: p = P ≠ 0.5
Nếu H0 bị bác bỏ, tức ứng dụng Chatbot AI có thể tác động lên độ hiệu quả trong quá trinh phục vụ khách hàng, và nếu H0 không bị bác bỏ, tức công ty không có cơ sở kết luận, cần thu thập thêm dữ liệu để phân tích thêm.
Giả định các khách hàng độc lập, hay nói cách khác ý kiến đánh giá của khách hàng này sẽ không tác động lên khách hàng kia.
Cách thức tính giá trị kiểm định. Chúng ta có S = số lượng các dấu (+) có được.
S = 11 trong ví dụ này có 11 dấu cộng.
Tiếp tục gọi n là số cặp cần xét, do chúng ta bỏ qua các trường hợp không dấu, nên n = 20 – 3 = 17.
Giá trị kiểm định được tính dựa trên phân phối nhị thức p = 0.5. Nếu giả thuyết H0 đúng thì phân phối của số lượng các dấu cộng sẽ có phân phối nhị thức với p = 0.5 và n = 17. p ở đây là xác suất có (+)
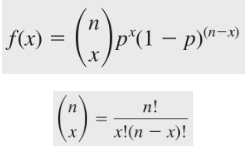
Công thức phân phối nhị thức hay công thức Bernoulli:
Với x = 0,1,2, …, n.
Ví dụ xác suất để có 5 dấu cộng trong n = 17.
P (x = 5) = [17!/ (5!*(17 – 5)!)]* [0.55(1 – 0.5)(17-5)] = 0.0472
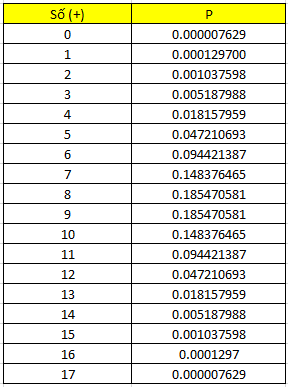
Các bạn có thể tính nhanh trên excel bằng cách sử dụng hàm Binomdist(x, 17,0.5,0), các bạn thay dần x = 0, 1, 2,… n vào công thức:
Kết quả như sau:
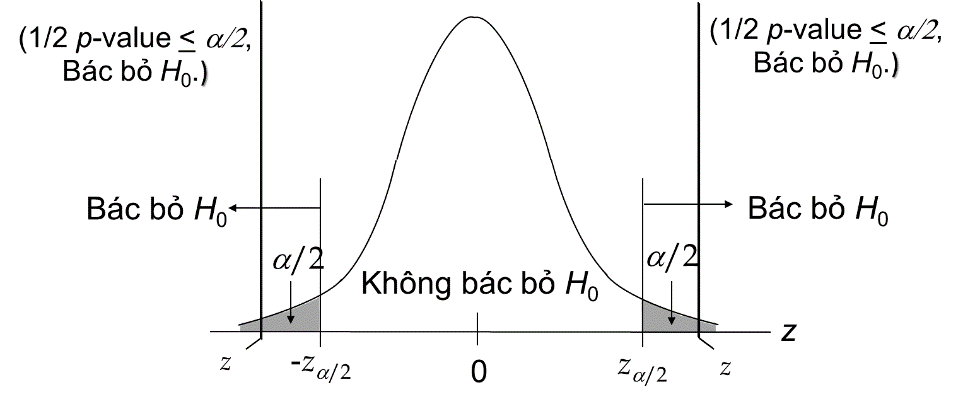
Nhắc lại một chút về kiểm định tham số thông thường. Các bạn cùng nhìn lại đồ thị hàm mật độ xác suất theo phân phối chuẩn Z áp dụng cho kiểm định tham số thông thường thì điều kiện để bác bỏ giả thuyết H0 đó là p < mức ý nghĩa α (cho kiểm định 1 phía), và p < mức ý nghĩa α/2 (cho kiểm định 2 phía)
H0: p = P =0.5 và H1: p = P ≠ 0.5
Với cách đặt giả thuyết như trên thì đây là kiểm định 2 phía.
*lưu ý lần nữa, các bạn nào chưa biết gì về các thuật ngữ liên quan đến kiểm định, cần xem lại và bổ sung thêm kiến thức cơ bản trước khi đọc tiếp nhé!
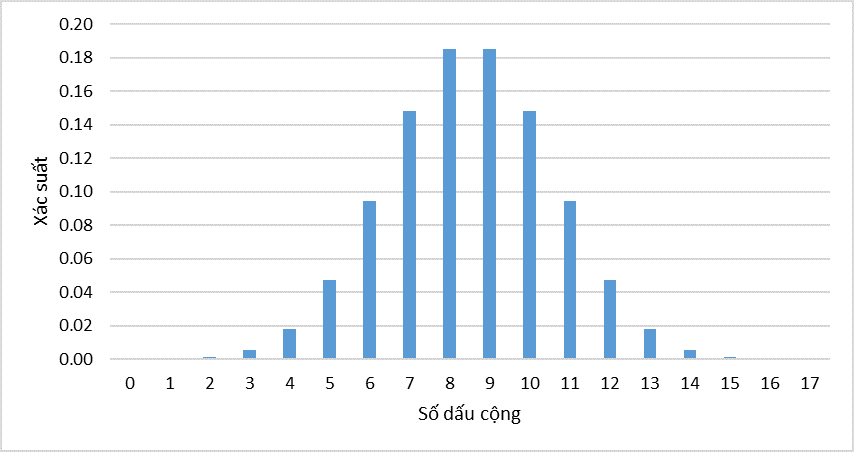
Trên hình là đồ thị hàm mật độ xác suất theo phân phối nhị thức, liên hệ ngược trở lại với quy tắc bác bỏ giả thuyết H0 của kiểm định tham số thông thường, chúng ta làm tương tự cho Sign – test. Nhưng khác biệt là chúng ta sẽ làm với số dấu cộng. Trước tiên chúng ta cần tính xác suất tích lũy.
Chúng ta kiểm định với độ tin cậy 95% và mức ý nghĩa α = 0.05, vậy điểm giới hạn bác bỏ H0 sẽ nằm ở α/2 = 0.05/2 = 0.025 do kiểm định 2 phía.
Chúng ta có xác suất để có nhỏ hơn 3 dấu (+) là P(X < 3) = P(0) + P(1) + P(2) = 0.00175 < 0.025.
Giới hạn ở đuôi trên sẽ là L1 = 3.
Chúng ta có xác suất để có nhiều hơn 14 dấu (+) là P(X > 14) = P(15) + P(16) + P(17) = 0.00175 < 0.025.
Giới hạn ở đuôi trên sẽ là L2 = 14.
Bác bỏ giả thuyết H0 khi:
- S < L1 hoặc S > L2 thì bác bỏ H0
- L1 < S < L2 thì không bác bỏ H0
Vì L1 = 3 < S = 11 < L2 = 14, không bác bỏ H0
Suy ra, trong thực tế, chúng ta không có bằng chứng hay cơ sở kết luận việc ứng dụng Chatbot AI có đem lại hiệu quả chăm sóc khách hàng tốt hơn.
Cách tính khác:
Ở hầu hết các dạng kiểm định chúng ta bác bỏ giả thuyết H0 khi p-value < α.
Kiểm định 2 phía nên chúng ta tính p-value xong rồi nhân cho 2 và so sánh với α
Chúng ta có S = 11 tức kết quả số dấu (+) nằm ở phía phải, chúng ta tính P (X ≥ 11) = P(11) + P(12) + … + P(17) = 0.166153.
P-value = 0.166153 * 2 = 0.332 > α. Chúng ta không thể bác bỏ H0 kết luận tương tự như trên.
Tiếp tục chúng ta cùng qua ví dụ khác:
Một công ty sản xuất điện thoại thông minh mới nâng cấp dòng điện thoại A, và khảo sát 10 khách hàng tại cửa hàng cho họ dùng thử và đưa ra đánh giá so với phiên bản cũ theo thang điểm từ 1-10, trên cơ sở những khách hàng này đã sử dụng điện thoại A phiên bản cũ.
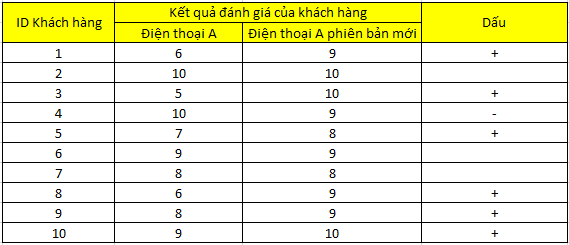
Bên trên là kết quả khảo sát. Công ty muốn tìm hiểu nhanh liệu có thể kết luận dòng điện thoại A mới tốt hơn hay không.
Đặt giả thuyết:
H0: p = P =0.5
H1: p = P ≥ 0.5
Các bạn để ý với ví dụ đầu thì thấy ở đây H1 có khác biệt khi sử dụng dấu ≥ 0.5, nghĩa là sự cải tiến dòng sản phẩm A mang lại kết quả tốt hơn.
Chúng ta tiến hành kiểm định 1 phía, đây là phía bên phải.
Xác suất tính theo phân phối nhị thức cho từng số (+)
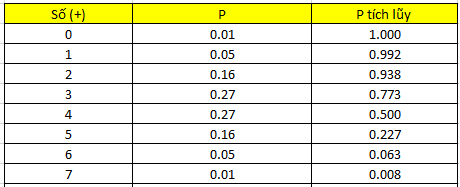
Do có 3 cặp dữ liệu ngang nhau nên chúng ta có n = 7, p = 0.5, tính tương tự như ví dụ đầu sẽ được kết quả như trên.
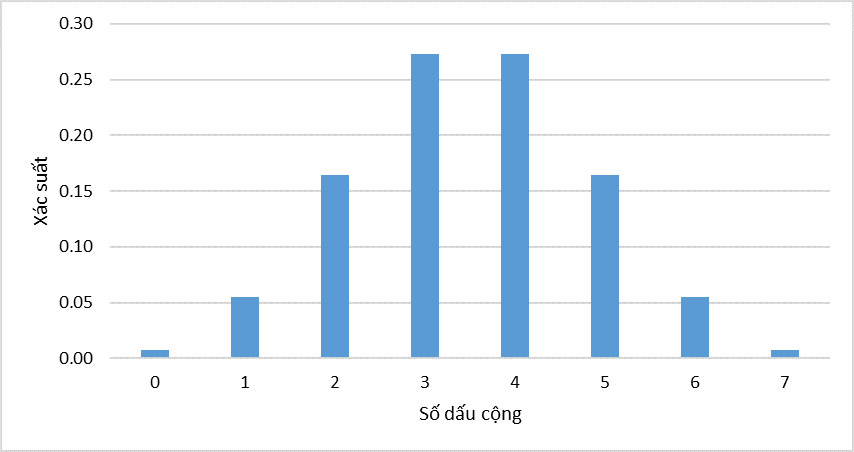
Do kiểm định 1 phía, phía đuôi bên phải, nên chúng ta cộng xác suất từ dưới lên ở phía bên phải, tức P(7) + P(6) + …., nếu tổng xác suất tính đến số dấu (+) gần nhất chưa vượt quá mức ý nghĩa α thì lấy số dấu (+) làm điểm giới hạn L
Để đơn giản quá trình tính toán chúng ta tính P tích lũy từ dưới lên. Tại P(5) = 0.227 < 0.05, nên L = 5
- Bác bỏ H0 khi S ≥ L
- Không bác bỏ H0 khi S < L
S = 6 > L = 5. Bác bỏ H0 tức có thể kết luận sản phẩm A mới tốt hơn sản phẩm B mới với độ tin cậy 95%.
*Trường hợp kiểm định 1 phía, phía bên trái, chúng ta làm ngược lại.
Ở bên trên chúng ta đã tìm hiểu qua 2 ví dụ nhưng với mẫu dữ liệu nhỏ hơn 20. Trong thực tế, mẫu dữ liệu có thể lớn hơn rất nhiều. Cũng giống như kiểm định tham số khi mẫu lớn hơn 20, Sign-test sẽ xấp xỉ phân phối chuẩn và sử dụng phân phối mẫu cho số dấu (+) tìm được thay cho phân phối nhị thức ban đầu của nó.
Chúng ta sử dụng công thức trong kiểm định tỷ lệ tổng thể.
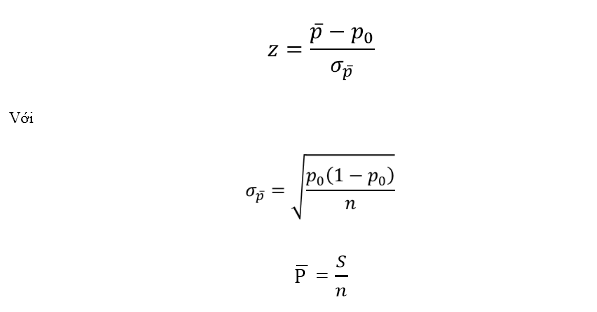
S là số dấu cộng, n là số cặp hay là số quan sát (bao gồm cả trường hợp không có dấu hay ngang dấu)
Một công ty tiến hành khảo sát 100 khách hàng đánh giá song song về sản phẩm nước giải khát mới dành cho người ăn kiêng, người bị tiểu đường có thêm vị ngọt (sản phẩm B), và sản phẩm nước giải khát không đường không có vị ngọt, chỉ có gas (sản phẩm A)
Dưới đây là kết quả tóm tắt từ 100 người khảo sát
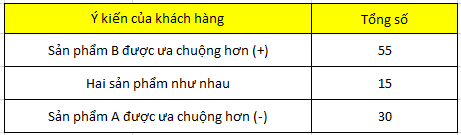
Đặt giả thuyết:
H0: p = P =0.5. Hai sản phẩm có mức độ ưa chuộng như nhau.
H1: p = P ≠ 0.5. Hai sản phẩm có mức độ ưa chuộng khác nhau
Các bạn thử tính theo công thức ở trên nhé với s = 55, n = 100. Kết quả kiểm định Z như sau:
Z = 1
Với mức ý nghĩa thường sử dụng là α = 0.05 chúng ta có Z0.05 = 1.96 tra từ bảng phân phối chuẩn Z. Quy tắc bác bỏ
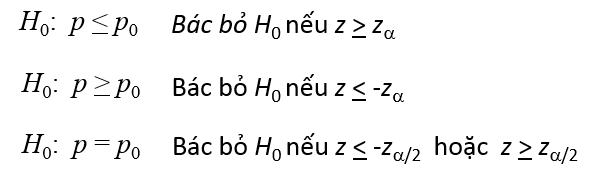
Z = 1 < Z0.05 nên chúng ta không có bác bỏ H0 nghĩa là chưa có đủ cơ sở để kết luận hai sản phẩm này có mức độ ưa chuộng khác nhau hay nói cách khác sản phẩm B chưa thể khẳng định hiệu quả hơn sản phẩm A.
Kiểm định Wilcoxon
Chúng ta đã biết đến kiểm định dấu Sign-test là dạng kiểm định phi tham số rất đơn giản, chỉ sử dụng dấu (+) để tính giá trị kiểm định nhưng đây cũng chính là điểm yếu của nó khi nó cần ít thông tin để phân tích đặc biệt là không đề cập đến độ lớn trong sự khác biệt của 2 yếu tố, 2 đối tượng, 2 nhóm đang xét hay nói cách khác áp dụng kiểm định giả thuyết từ mẫu cặp.
Ví dụ như khi nói về kết quả đánh giá 2 sản phẩm khảo sát từ một nhóm khách hàng như ở Sign test, chúng ta chỉ quan tâm đến dấu (+) mà không biết liệu có sự khác biệt về lượng cụ thể hay không.
Kiểm định phi tham số Wilcoxon mạnh hơn Sign-test ở chỗ nó định lượng sự khác biệt và đưa chúng vào phân tích. Wilcoxon khá giống kiểm định tham số áp dụng cho 2 mẫu.
Cũng giống như các phương pháp kiểm định phi tham số khác, Wilcoxon không yêu cầu đưa ra bất kỳ giả định nào về quy luật phân phối nào cả. Nó giúp kiểm định sự khác biệt trong quy luật phân phối của 2 tổng thể.
Kiểm định phi tham số Wilcoxon sử dụng dữ liệu định lượng và kiểm tra giả thuyết về trung vị của tổng thể nghiên cứu, thay vì sử dụng giá trị trung bình trong kiểm định tham số thông thường. Giải thích đơn giản, trung vị là giá trị đại diện, nằm ở vị trí chính giữa của một tổng thể có các giá trị được sắp xếp theo thứ tự. Và trong tổng thể đó sẽ có một nửa số các giá trị nhỏ hơn trung vị và một nửa số các giá trị lớn hơn trung vị. Hay nói đơn giản là quy luật phân phối phải được xác định từ tổng thể.
Nếu 2 đối tượng hay 2 tổng thể nghiên cứu giống nhau thì 2 trung vị của chúng hay quy luật phân phối các giá trị phải theo quy tắc trên. Khi 2 trung vị khác nhau hay không bằng nhau thì chứng tỏ có sự khác biệt.
Chúng ta cùng đi qua ví dụ cụ thể.
Quay lại với ví dụ liên quan đến Chatbot AI. Công ty triển khai ứng dụng Chatbot AI nhưng phát sinh vấn đề đó là Chatbot AI không phải câu hỏi nào của khách hàng cũng trả lời được. Nhân viên CSKH phải vào hệ thống trả lời thay. Điều công ty quan tâm là tốc độ nhân viên phản hồi lại khách hàng thông qua Chatbot AI có nhanh hơn tốc độ nhân viên phản hồi khi khách hàng khi không ứng dụng Chatbot AI vào nền tảng nhắn tin hay không.
Nếu nhân viên phản hồi khách hàng chậm hơn có thể do Chatbot AI báo thông tin về trễ hoặc, bị lỗi trong việc chuyển lại câu hỏi khách hàng đến nhân viên phụ trách. Nếu tốc độ phản hồi nhanh hơn chứng tỏ Chatbot AI hoạt động tốt.
Dưới đây là kết quả đo lường thu về từ 20 nhân viên CSKH trong tháng vừa qua, thời gian phản hồi tính trên trung bình tháng.
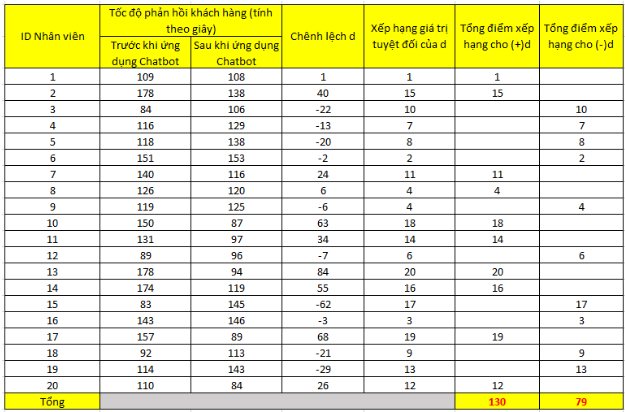
Các bước làm kiểm định như sau:
Đầu tiên chúng ta đặt giả thuyết:
H0: Hai giá trị trung vị của thời gian phản hồi KH trước và sau khi ứng dụng Chatbot AI là bằng nhau. (không có sự khác biệt)
H1: Hai giá trị trung vị của thời gian phản hồi KH trước và sau khi ứng dụng Chatbot AI không bằng nhau (Chatbot AI đem lại hiệu quả tốt hơn) – Đây là kiểm định 1 phía
Tiếp theo chúng ta tìm khoảng chênh lệch hay giá trị chênh lệch giữa thời gian phản hồi KH trước và sau khi ứng dụng Chatbot AI
Ví dụ d1 = 109 – 018 = 1
Sau khi tính toán tất cả các chênh lệch thì việc tiếp theo đó là xếp hạng chúng, lưu ý sử dụng giá trị tuyệt đối để xếp hạng ví dụ (-22) lấy trị tuyệt đối sẽ bằng 22, xếp hạng thứ 10 trong dãy số từ 1 đến 84.
Trường hợp nếu trùng giá trị, chúng ta sẽ đếm theo thứ tự và tính trung bình: ví dụ có 3 số 1, 1, 1. Giả sử số 1 đầu tiên có hạng là 3, thì số 1 tiếp theo có hạng là 4, còn lại là hạng 5. Trung bình sẽ là (3 + 4 + 5)/3 = 4, vậy cả 3 số 1 này đều có hạng là 4.
Tiếp tục chúng ta tính tổng điểm xếp hạng cho các chênh lệch (+) và (-) thực tế ở cột chênh lệch d.
Cúng ta tìm giá trị Tmin trong T(+) và T(-). T(+) chính là tổng điểm xếp hạng của các chênh lệch (+) và T(-) là tổng điểm xếp hạng của các chênh lệch (-)
Tmin = min [T(+), T(-)] = min (130, 79)
Tiếp theo tra bảng Wilcoxon với n = 20, nếu có chênh lệch d = 0, chúng ta sẽ bỏ qua trường hợp này, và trừ vào n. Ở đây không có d = 0, nên n = 20
Tra bảng Wilcoxon, ở một số tài liệu thống kê có thể không đề cập đến bảng phân phối Wilcoxon ở phần Appendix, và ở các tài liệu khác nhau các bảng Wilcoxon có thể khác nhau, do đó cần 1 bảng tiêu chuẩn.
Bảng Wilcoxon chúng tôi giới thiệu ở đây là bảng Wilcoxon tham khảo từ chuyên gia R. L. McCormack, là tác giả của “Extended tables of the Wilcoxon matched pairs signed rank statistics,” được đề cập trong tạp chí “The American Statistical Association” (1965).
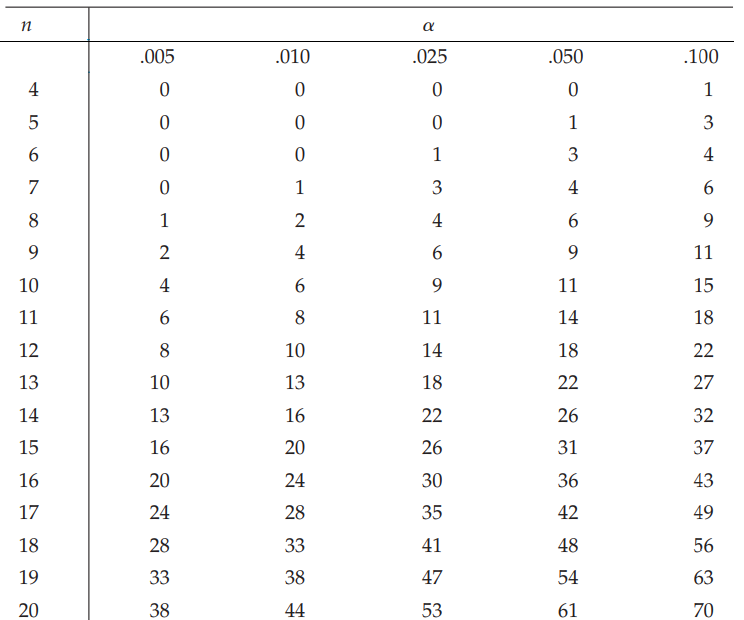
Vì là kiểm định 1 phía nên chúng ta không cần chia 2 mức ý nghĩa α, giữ nguyên α = 0.05.
T tra bảng với n = 20, sẽ có giá trị là 61
Quy tắc bác bỏ H0 : T ≤ Ttra bảng cho cả 2 trường hợp kiểm định 2 phía, và 1 phía
T = 79 > Ttra bảng Do đó chúng ta không bác bỏ H0 và kết luận chưa có cơ sở khẳng định Chatbot AI giúp tăng tốc độ phản hồi của khách hàng.
Sử dụng p-value, thì cách tính p-value, các bạn tra n = 20, và T = 79, nhìn bảng ta thấy khi mức ý nghĩa tăng thì T tăng với điều kiện cùng n, như vậy T = 79 thì p-value có thể > 0.1 và dĩ nhiên > α = 0.05 mà bác bỏ H0 khi p-value < 0.05. Nên ở đây cũng không bác bỏ H0, kết luận tương tự như trên
Wilcoxon còn được gọi là Signed – rank test, vì nó sử dụng kết quả xếp hạng chênh lệch và dấu của chênh lệch, nguyên lý hoạt động của nó khá phức tạp chúng tôi không thể trình bày ở đây do bài viết có giới hạn.
Các bạn chỉ cần nhớ các bước và công thức là đã tốt lắm rồi không nhất thiết phải đi tìm hiểu chi tiết, bản chất của kiểm định Wilcoxon nữa đâu.
Chúng ta vừa đi qua ví dụ với mẫu dữ liệu nhỏ, còn với mẫu dữ liệu lớn thì như thế nào?
Khi mẫu dữ liệu có số quan sát lớn, thông thường lớn hơn 20, phân phối chuẩn có thể được sử dụng để thay thế cho Wilcoxon.
Công thức tính trung bình, phương sai của phân phối Wilcoxon
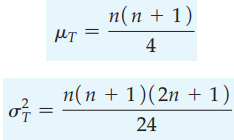
Công thức kiểm định:
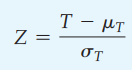
T chính là Tmin của (tổng hạng (+); tổng hạng (-)), n là số quan sát hay số cặp mà ở đó d khác 0, tức các trường hợp không có dấu (+), hay không có (-) sẽ bị loại bỏ.
Với H0: không có sự khác biệt giữa 2 nhóm/ tổng thể nghiên cứu
Quy tắc bác bỏ H0 cũng tương tự như kiểm định Z thông thường.
Z ≥ Zα/2 hay Z ≤ – Zα/2 cho kiểm định 2 phía, và Z ≥ Zα cho kiểm định 1 phía bên phải, và Z ≤ – Zα cho kiểm định 1 phía bên trái.
Việc quan trọng đó là tìm ra được giá trị T chính xác để thay vào công thức, cách xếp hạng sai sẽ dẫn đến bài toán sai khi T chắc chắn sẽ sai.
Do công thức khá đơn giản, cũng như cách xếp hạng cho các chênh lệch d các bạn cũng đã biết nên chúng tôi sẽ không trình bày thêm ví dụ ở phần này.
Kiểm định Mann – Whitney
Từ đầu bài viết đến giờ chúng ta đã làm quen 2 dạng kiểm định phi tham số áp dụng cho mẫu cặp, dữ liệu khảo sát từ một nhóm nhưng chia làm 2 lần hay 2 giai đoạn, mỗi lần, mỗi giai đoạn sẽ có thứ được thử nghiệm, đánh giá.
Kiểm định phi tham số Mann – Whitney test hay còn gọi là U test giống kiểm định Wilcoxon về nguyên lý hoạt động (cùng dựa trên sự so sánh độ tập trung hay phân tán, và đặc biệt là trung vị giữa 2 tổng thể; và không cần đưa ra các giả thuyết về quy luật phân phối) nhưng nó áp dụng cho trường hợp 2 mẫu độc lập., kiểm định giả thuyết từ 2 tổng thể độc lập.
Chúng ta cùng đi vào ví dụ cụ thể:
Một công ty bán lẻ điều hành một trung tâm thương mại muốn tìm hiểu trong ngày Valentine, chi tiêu của các khách hàng nam và nữ cho những dòng sản phẩm dành riêng cho các cặp đôi là như thế nào có khác biệt hay không. Trung tâm thương mại lấy thông tin nhanh của 10 khách hàng nam và 10 khách hàng nữ có thẻ thành viên, và những người này tiến hành thanh toán tại khu vực trưng bày các sản phẩm đó. Kết quả thu được như sau:
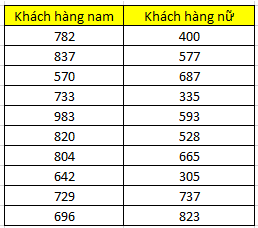
Đầu tiên chúng ta đặt giả thuyết:
H0: chi tiêu cho các sản phẩm dành cho các cặp đôi của nhóm khách hàng nam và nữ là như nhau
H1: chi tiêu cho các sản phẩm dành cho các cặp đôi của nhóm khách hàng nam và nữ là khác nhau
Cách đặt giả thuyết theo trung vị Me
H0: Me1 = Me2
H1: Me1 ≠ Me2
Mức ý nghĩa α = 0.05, độ tin cậy 95%
Chúng ta sẽ tiến hành xếp hạng cho 20 quan sát, sau đó phân lại các quan sát cũng như hạng của chúng vào nhóm nam và nữ ban đầu
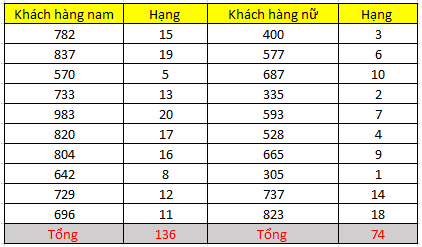
Tiếp theo tính giá trị kiểm định phi tham số theo công thức:
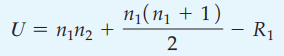
U = 10*10 + (10*11)/2 – 136 = 19
Với 2 mẫu có quan sát ít nhất 10 người, Mann – Whitney có thể xấp xỉ phân phối chuẩn với
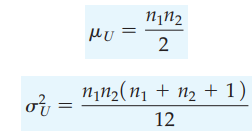
Theo công thức tính:
µ = (10*10)/2 = 50
σ = 13.22
Công thức kiểm định Z:
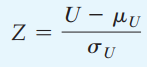
Theo công thức tính:
Z = – 2.34
Tra bảng Zα/2 do kiểm định 2 phía, Z0.025 = 1.96
Bác bỏ H0 khi Z ≥ Zα/2 hay Z ≤ – Zα/2 cho kiểm định 2 phía, và Z ≥ Zα cho kiểm định 1 phía bên phải, và Z ≤ – Zα cho kiểm định 1 phía bên trái.
Kiểm định 2 phía, lấy trị tuyệt đối Z = -2.34 để so sánh: 2.34 > 1.96
p-value = [1 – (0.9904)] *2 = 0.0192 < 0.05, thỏa điều kiện bác bỏ
Hoặc Z < – Zα/2 => -2.34 < -1.96
Như vậy chúng ta có thể bác bỏ H0 và kết luận số tiền chi tiêu của khách hàng nam và nữ cho các sản phẩm dành cho cặp đôi là khác nhau.
Giả sử công ty nghi ngờ chi tiêu của khách hàng nam là cao hơn khách hàng nữ, đặt lại giả thuyết
H0: Me1 ≤ Me2
H1: Me1 ≥ Me2
Tra bảng Zα = 1.65. Chúng ta có giá trị kiểm định Z = -2.34
Suy ra Z < Zα, không bác bỏ H0 chưa đủ chứng cứ để kết luận khách hàng nam chi tiêu nhiều hơn.
Kruskal – Wallis test
Dạng kiểm định này sử dụng nhiều trong phân tích phương sai ANOVA, dùng để kiểm tra mối liên hệ giữa 2 yếu tố, nhóm, nói cách khác là kiểm tra tác động của 1 yếu tố nguyên nhân lên yếu tố kết quả nào đó.
Nếu kiểm định U, hay Wilcoxon kiểm tra sự khác biệt giữa 2 tổng thể, thì đây là dạng kiểm định phi tham số được dùng để kiểm tra sự khác biệt của nhiều hơn 2 tổng thể.
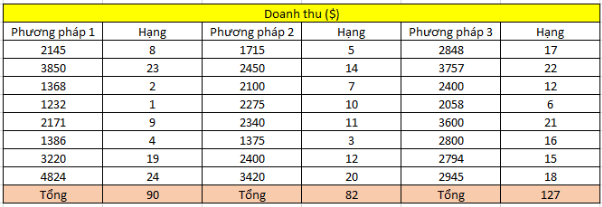
Một công ty sản xuất, phân phối sản phẩm dược triển khai ứng dụng 3 phương pháp Marketing khác nhau, phương pháp 1: thông qua Website, fanpage, phương pháp 2: thông qua các sự kiện offline giới thiệu sản phẩm, phương pháp 3: thông qua kênh CSKH tự động (Chatbot). Doanh thu mỗi ngày được thu thập như trên.
H0: doanh thu mang về từ các phương pháp Marketing là như nhau.
H1: các phương pháp Marketing mang về doanh thu khác nhau
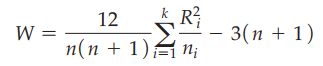
Giá trị kiểm định sẽ được so sánh với giá trị tra bảng từ phân phối chi bình phương (Chi-squared) mà chúng ta đã được biết đến ở bài viết trước.
n là tổng số quan sát, ni là số quan sát trong mỗi nhóm i
Ri là tổng hạng ở mỗi nhóm
W tính được sẽ bằng: 2.3825
Tra bảng chi bình phương với df = k – 1= 3 – 1 = 2 k là số nhóm, α = 0.05
χ22, 0.05 = 5.991
Giá trị W < χ22, 0.05 nên chúng ta không bác bỏ H0, các phương pháp marketing mang lại doanh thu giống nhau, và công ty cần thêm thông tin để chứng minh điều ngược lại. Sự thay đổi, nâng cấp các phương pháp marketing tiên tiến như phương pháp 1, và phương pháp 3 không ảnh hưởng lên doanh thu nếu nhìn vào kết quả kiểm định
Thực tế, doanh thu trung bình ngày của phương pháp 1 là 2525 $, của phương pháp 2 là 2260 $ và phương pháp 3 là 2900$.
Doanh thu không khác biệt quá lớn, nên có thể suy luận việc thay đổi phương pháp marketing có thể mang lại hiệu quả, và sự thay đổi trong phương pháp có mang lại ảnh hưởng nhất định. Nhưng công ty cần thêm dữ liệu để phân tích sâu hơn.
Đến đây là kết thúc bài viết về kiểm định phi tham số. Hẹn gặp lại các bạn ở những bài viết khác.
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English