Trở lại với các bài viết của BigDataUni, bài viết lần này chúng ta sẽ tìm hiểu về kiểm định phi tham số cụ thể là kiểm định chi bình phương (Chi-square test). Trong series về phương pháp phân tích sống sót (Survival analysis) chúng tôi từng nhắc đến sự khác biệt giữa các mô hình tham số (parametric models) và phi tham số (non-parametric models). Đối với mô hình tham số, chúng ta phải đưa ra giả định ban đầu về bộ tham số được đưa vào mô hình, quy luật phân phối xác suất áp dụng cho các đối tượng nghiên cứu trong tập dữ liệu. Tuy nhiên nếu chưa thể đưa ra các giả định, đặc biệt trường hợp dữ liệu thu thập là dữ liệu định tính, thì mô hình phi tham số sẽ được ưu tiên sử dụng.
Tương tự trong lý thuyết thống kê, khi tiến hành kiểm định tham số cho các kết quả thu được từ những nghiên cứu, chúng ta cần xét điều kiện được quan tâm là tổng thể nghiên cứu có phân phối chuẩn. Tuy nhiên trường hợp, người làm phân tích theo kinh nghiệm của mình cho rằng tổng thể nghiên cứu thực tế không phải như vậy, họ có quyền không đưa ra giả định. Hay tổng thể nghiên cứu về bản chất đã không thỏa điều kiện này, thì các phương pháp kiểm định tham số không thể đưa vào sử dụng, thay vào đó là kiểm định phi tham số.

Kiểm định phi tham số hay non-parametric hypothesis tests hỗ trợ kiểm định giả thuyết liên quan đến tổng thể nghiên cứu mà ở đó không mang bất kỳ giả định nào về quy luật phân phối, hay có quy luật phân phối bất kỳ không theo phân phối chuẩn, và không cần bất kỳ tham số nào như trung bình, độ lệch chuẩn, tỷ lệ,…thường áp dụng cho dữ liệu định tính hơn là dữ liệu định lượng. Các phương pháp kiểm định phi tham số đã xuất hiện từ rất lâu từ cuối những năm 1940 và vẫn còn hữu dụng cho đến ngày hôm nay.
Trong 2 bài viết lần này về kiểm định phi tham số, chúng ta sẽ cùng tìm hiểu đến một vài phương pháp kiểm định phi tham số quan trọng như Sign – test, Wilcoxon – rank test, Mann – Whitney test, Kruskal – Wallis test, và đặc biệt là kiểm định Chi bình phương Chi – squared test được ứng dụng phổ biến hơn mà chúng ta thường nhắc đến ở các chủ đề bài viết trong Data mining mà gần nhất là Survival analysis. Chúng ta sẽ tìm hiểu Chi-squared test với các ví dụ đơn giản trong phần 1 bài viết lần này.
Các lý thuyết liên quan đến thống kê, cũng như quy luật phân phối, lý thuyết kiểm định tham số như kiểm định là gì, vì sao cần, … chúng tôi sẽ không đề cập lại chi tiết. Các bạn có thể xem lại các bài viết qua link dưới đây:
Tổng quan về Statistics: Khái niệm và ứng dụng của thống kê
Tổng quan về Statistics: Descriptive statistics (thống kê mô tả)
Tổng quan về Statistics: Inferential statistics (thống kê suy luận)
Tìm hiểu về phương pháp kiểm định tham số
Các dạng kiểm định tham số (trường hợp 1 mẫu)
Các dạng kiểm định tham số (trường hợp 2 mẫu)
Kiểm định chi bình phương (Chi-squared test)
Kiểm định chi bình phương áp dụng cho dạng dữ liệu thống kê theo dạng tần số. Mục đích ứng dụng phổ biến của kiểm định chi bình phương đầu tiên là kiểm tra xem có mối liên hệ, mối quan hệ giữa 2 biến, 2 yếu tố đang xét đến. Nhu cầu kiểm tra mối liên hệ giữa 2 biến xuất hiện nhiều trong các phương pháp phân tích như hồi quy Logistics, Survival analysis,… và trong thực tế khi chúng ta quan tâm đến sự khác biệt giữa 2 nhóm đối tượng nghiên cứu thuộc lĩnh vực xã hội, kinh tế.
Một ứng dụng khác của kiểm định chi bình phương đó là “Goodness of Fit” dùng để kiểm tra giả định về quy luật phân phối trong một tổng thể nghiên cứu có đúng không, có hợp lý hay không ví dụ kiểm tra giả định chi tiêu trung bình của khách hàng cho các sản phẩm của công ty mỗi tháng tuân theo phân phối chuẩn. Hay ví dụ cụ thể, một chuyên viên phân tích bán hàng của một công ty cho rằng tỷ lệ doanh thu của sản phẩm A, B, C tuân theo phân phối đa thức (Multinominal probability distribution) lần lượt là 40%, 25%, 35%.
Chúng ta sẽ sử dụng kiểm định chi bình phương để kiểm tra kết luận của chuyên gia phân tích có đúng không.
Giả sử công ty sản xuất smartphone có 3 dòng sản phẩm A, B, C, có mức giá trung bình ngang nhau, không quá chênh lệch, dành cho phân khúc khách hàng tầm trung, được khách hàng chọn lựa dựa trên các yếu tố thiết kế, tính năng. Tỷ lệ doanh số phân khúc tầm trung trong năm 2019 lần lượt là 40%, 25%, 35%.
Trong năm 2020, dòng sản phẩm B được công ty thiết kế, sáng tạo thêm các tính năng mới như camera AI, nhận diện khuôn mặt. Công ty muốn tìm hiểu liệu việc sản phẩm B được cải tiến như vậy sẽ tác động lên doanh thu của sản phẩm A, C như thế nào.
Công ty tiến hành thu thập dữ liệu 300 khách hàng, mỗi khách hàng mua 1 trong 3 sản phẩm A, B, C. Chúng ta có phân phối đa thức với tỷ lệ doanh số cụ thể pA, pB, pC.
Nói một chút về phân phối đa thức (Multinominal probability distribution), đây là quy luật phân phối mở rộng từ phân phối nhị thức (Binominal probability distribution). Ví dụ trong phân phối nhị thức, chúng ta có xác suất khách hàng mua sản phẩm A: pA và xac suất không mua sản phẩm A sẽ là 1 – pA; và pA + (1 – pA) = 1. Đối với đa thức, chúng ta có thể xét nhiều hơn các kết quả đạt được, như ví dụ ở trên, nếu khách hàng không mua A, thì họ có thể mua B hoặc C; không mua B, thì có thể mua A hoặc C; không mua C, thì có thể mua A hoặc B. Chúng ta sẽ có pA – xác suất mua sản phẩm A, pB, pC lần lượt là xác suất mua sản phẩm B, xác suất mua sản phẩm C.
Với pA + pB + pC = 1
Quay trở lại với bài toán, chúng ta sẽ đặt giả thuyết:
H0: Doanh số của 3 sản phẩm A, B, C tuân theo phân phối đa thức với tỷ lệ doanh số hay xác suất khách hàng mua sản phẩm A, B hoặc C lần lượt là pA = 0.4 pB = 0.25 pC = 0.35
H1: Doanh số của 3 sản phẩm A, B, C không tuân theo phân phối đa thức với tỷ lệ doanh số hay xác suất khách hàng mua sản phẩm A, B hoặc C lần lượt là pA = 0.4 pB = 0.25 pC = 0.35
Hoặc đơn giản:
H0: pA = 0.4; pB = 0.25; pC = 0.35
H1: tỷ lệ doanh số ứng với 3 sản phẩm A, B, C sẽ không phải là pA = 0.4 pB = 0.25 pC = 0.35
Cách thực hiện
Kiểm định chi bình phương hoạt động dựa trên sự khác biệt giữa số quan sát thực tế (tần suất thực tế) – Observed, ký hiệu Oi; và số quan sát mong đợi hay dự kiến (tần suất mong đợi dự kiến) – Expected, ký hiệu Ei. Với i là nhóm đang xét.
Từ “mong đợi”, hay “dự kiến” được hiểu đơn giản như sau. Ví dụ nếu công ty không tiến hành cải tiến sản phẩm B, thì tỷ lệ doanh số của 3 sản phẩm A, B, C trong năm 2020 có thể được mong đợi sẽ tối thiểu bằng 2019. Hoặc nếu không có gì xảy ra trong năm 2020, tỷ lệ doanh số 3 sản phẩm A, B, C dự kiến sẽ bằng năm trước.
Công thức kiểm định Chi-squared quen thuộc mà chúng tôi từng đề cập ở các chủ đề bài viết trước:
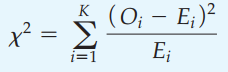
Oi là số quan sát trong thực tế, Ei = n*p là số quan sát dự kiến, với n là tổng số đối tượng có trong mẫu, p là tỷ lệ hay xác suất cho trước, có trong giả thuyết H1
Kết quả thu thập được như sau: sản phẩm A: 100 khách hàng chọn, sản phẩm B là 110; sản phẩm C là 90
Chúng ta lập bảng tính như sau:

Số sản phẩm là 3, suy ra bậc tự do df = k – 1 = 3 – 1 = 2 với k là số nhóm
Chúng ta tra bảng chi bình phương để tìm p-value, thì sẽ thấy

Với χ2 = 21.8 > 10.597 rất nhiều nên p-value < 0.005 và chắc chắn < mức ý nghĩa α = 0.05, nên chắc chắn chúng ta sẽ bác bỏ H0 kết luận: sự cải tiến của sản phẩm B đã tác động làm thay đổi tỷ lệ doanh số.
Chúng ta có thể so sánh giá trị kiểm định χ2 = 21.8 với giá trị tra bảng tại df = 2, α = 0.05 là 5.991. χ2 = 21.8 > 5.991 nên chúng ta bác bỏ H0
Tỷ lệ doanh số đã thay đổi: pA = 100/300 = 0.33; pB = 0.37; pC = 0.30
Kết luận, doanh số trung bình của các sản phẩm không tuân theo phân phối đa thức với pA = 0.4; pB = 0.25; pC = 0.35.
Cơ cấu doanh số sản phẩm của 3 sản phẩm A, B, C đã bị thay đổi khi sản phẩm B được cải tiến, cụ thể:
- Tỷ lệ doanh số A giảm từ 40% xuống 33%
- Tỷ lệ doanh số B tăng mạnh từ 25% lên 37%
- Tỷ lệ doanh số của C giảm nhẹ từ 35% xuống 30%
Chúng ta cùng đi qua ví dụ khác. Giả sử một chuyên gia phân tích đến từ một công ty bán lẻ muốn tìm hiểu mức chi trung bình hàng tháng tại cửa hàng của một khách hàng có theo quy luật phân phối chuẩn hay không.
Mức chi tiêu được phân là 5 khoảng, hay 5 nhóm như sau:
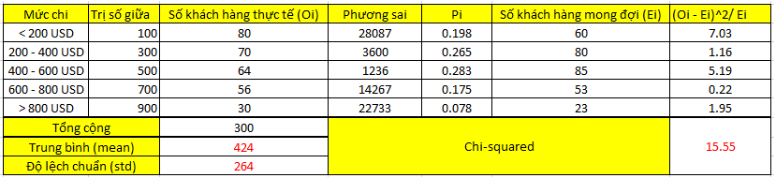
Chúng ta đặt giả thuyết
H0: số tiền mỗi khách hàng chi cho cửa hàng trong 1 tháng theo phân phối chuẩn
H1: số tiền mỗi khách hàng chi cho cửa hàng trong 1 tháng không theo phân phối chuẩn
Chúng ta tính trung bình mean x = (80*100 + 70*300 + … + 30*900)/ 300 = 424
Độ lệch chuẩn = (tổng các phương sai)1/2 = 264
Tổng phương sai = [(100 – 424)^2 / (300 – 1)]*80 + … + [(900– 424)^2 / (300 – 1)]*30 = 69924
*Công thức tính trung bình, độ lệch chuẩn, phương sai ở các bài viết thống kê của chúng tôi:
Tổng quan về Statistics: Khái niệm và ứng dụng của thống kê
Tổng quan về Statistics: Descriptive statistics (thống kê mô tả)
Tổng quan về Statistics: Inferential statistics (thống kê suy luận)
Công thức tính số khách hàng mong đợi Ei = n*Pi
Với Pi là xác suất tính được từ hàm mật độ xác suất trong phân phối chuẩn (Normal distribution), các bạn xem lại chi tiết phân phối chuẩn trong bài viết thống kê suy luận của chúng tôi.
Dựa theo công thức trong quy luật phân phối chuẩn, chúng ta tính lần lượt P(X<200), P(200<X<400), P(400<X<600), P(600<X<800), P(X>800). Tổng các xác suất sẽ bằng 1
Chuẩn hóa các giá trị của biến X bằng công thức Z-score:
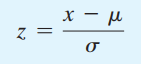
Hàm mật độ xác suất sẽ đơn giản:
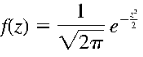
Xác suất của X sẽ được tính bằng xác suất của Z với công thức tích phân
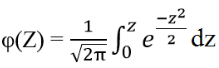
Phân phối chuẩn chuyển thành phân phối chuẩn tắc với giá trị trung bình µ =0, σ2 = 1, sử dụng các công thức trên. Chúng tính thử P(200<X<400) với trung bình là 424, độ lệch chuẩn 264
P(200<X<400) = P (((200 – 424)/264) ≤ Z ≤ ((400 – 424)/264)) = P (-0.85 ≤ Z ≤ -0.09)
= φ (-0.09) – φ (-0.85) = φ (-0.09) + φ (0.85) = 0.302 – 0.035 = 0.266
Tiếp tục chúng ta tính Ei = n*Pi như đã nói ở trên. Sau khi có Ei, công việc tiếp theo làm giống như ví dụ ban đầu.
Chúng ta có giá trị kiểm định chi bình phương là 15.55. Bậc tự do là k – 1 – số tham số, với k là số nhóm, số tham số trong phân phối chuẩn sử dụng trung bình, và độ lệch chuẩn nên bằng 2.
df = k – 1 – 2 = 5 – 3 = 2
với mức ý nghĩa α = 0.05, giá trị tra bảng là 5.991 < 15.55. Nên chúng ta bác bỏ H0 tức khả năng số tiền mỗi khách hàng chi cho cửa hàng trong 1 tháng không theo phân phối chuẩn.
Lưu ý thêm, ngoài áp dụng để kiểm định sự phù hợp của giả thuyết tổng thể nghiên cứu có phân phối chuẩn, thì kiểm định chi bình phương còn có thể áp dụng để kiểm tra tính phù hợp của các phân phối khác ví dụ như phân phối Poisson. Các bạn có thể tham khảo thêm ở những tài liệu khác.
Chúng ta đã đi qua 2 ví dụ sử dụng kiểm định chi bình phương để kiểm tra độ phù hợp của quy luật phân phối tiếp theo chúng ta qua ví dụ sử dụng Chi-squared test trong kiểm tra mối liên hệ giữa 2 yếu tố.

Công ty đang tìm hiểu liệu có mối quan hệ giữa thu nhập của khách hàng với các doanh số các sản phẩm phân loại theo giá. Ví dụ có 41 khách hàng thu nhập cao mua sản phẩm C giá cao, và 40 khách hàng có thu nhập thấp.
Chúng ta đặt giả thuyết
H0: Không có mối quan hệ giữa yếu tố giá cả và thu nhập
H1: Có mối quan hệ giữa yếu tố giá cả và thu nhập
Các số liệu trong bảng chính là số quan sát thực tế Oi theo như công thức kiểm định chi bình phương chúng ta phải tính toán số quan sát lý thuyết hay mong đợi Ei.
Công thức như sau:
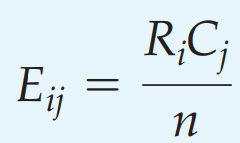
Với Cjsố quan sát thực tế tại cột j, Ri là số quan sát thực tế tại dòng i.
Số khách hàng mua sản phẩm B là 108, chiếm tỷ lệ là 108/300 = 36%, tương tự sản phẩm A sẽ là 27%, sản phẩm C là 37%. Trong trường hợp giả thuyết H0 đúng, và giá cả với thu nhập không có mối quan hệ với nhau hay nói cách khác các khách hàng có thu nhập khác nhau sẽ có khả năng mua sản phẩm B, A hay C là như nhau, hoặc tỷ lệ doanh số của sản phẩm B là như nhau ở các nhóm khách hàng có thu nhập khách nhau.
Ví dụ ở nhóm khách hàng thu nhập thấp thì tỷ lệ mua sản phẩm B sẽ phải bằng 36%, hiện tại là 35/100 = 35%. Như vậy để tỷ lệ mua sản phẩm B ở nhóm khách hàng thấp, chúng ta sẽ phải lấy 100*36% = 36
Suy ra theo công thức:
E21 = (108*100)/ 300 = 36. Với R2 = 108, C1 = 100
Tính tương tự cho các giá trị còn lại, chúng ta có bảng sau:

Các bạn phải đảm bảo cho dù có tính Ei thì các tổng số sẽ phải vẫn phải bằng các số liệu ban đầu của bài toán. Chúng ta đã có Oi và Ei vậy nên tính giá trị kiểm định chi bình phương như thế nào?
Chúng ta cùng đi qua công thức tiếp theo:
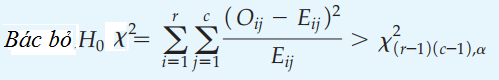

Cách tính, chúng ta tính từng ô. Ví dụ E11 = [(25 – 37)^2]/ 37 = 3.89
Sau đó tính tổng tất cả: Chi-square = E11 + E12 + … + E33 = 15.6. Đây sẽ là giá trị kiểm định tìm được. Tiếp theo chúng ta tìm giá trị tra bảng chi bình phương với bậc tự do (r – 1)*(c – 1) với r = 3, c = 3, suy ra df = 4. Mức ý nghĩa α ở đây chúng ta chọn là 0.05.
Giá trị tra bảng là 9.488. như vậy 15.6 > 9.488, suy ra bác bỏ H0 tức chúng ta tạm kết luận có mối quan hệ giữa thu nhập của các khách hàng với doanh số của sản phẩm A, B, C hay nói cách khác, rộng hơn, thu nhập của khách hàng có thể tác động lên nhu cầu mua điện thoại của họ, và giá cả vẫn đóng yếu tố cho việc quyết định mua hàng.
Quay lại bảng số liệu ban đầu:

Chúng ta chuyển thành tỷ lệ để dễ so sánh hơn

Khách hàng có thu nhập cao thì dĩ nhiên họ không cần mua điện thoại giá rẻ như điện thoại A, tỷ lệ chỉ có 22% mà thôi. Ngược lại họ mua điện thoại với mức giá từ trung bình trở lên với tỷ lệ là 78%. Tương tự nhóm khách hàng có thu nhập thấp thì khả năng họ mua điện thoại giá thấp sẽ cao hơn các sản phẩm kia, khả năng mua sản phẩm mắc tiền hơn như từ sản phẩm B, và C sẽ thấp hơn. Điều bất ngờ, là khách hàng có mức thu trung bình thì tỷ lệ mua sản phẩm C có mức giá cao ngang ngửa với các khách hàng có thu nhập cao.
Chúng tôi cố tình đưa ví dụ như vậy để minh họa cho các bạn thấy trong thực tế khi kiểm tra liệu có mối quan hệ giữa các yếu tố với nhau không chúng ta không nên dựa vào mỗi kiểm định chi bình phương để đưa ra kết luận, cần phải kết hợp nhiều công cụ khác đặc biệt cũng cần sử dụng góc nhìn thực tế. Việc xem xét mối quan hệ hình thù ra sao không phải là nhiệm vụ của kiểm định chi bình phương. Kiểm định chi bình phương chỉ giúp ta khẳng định là có hay không có sự tồn tại của mối quan hệ.
Do đó thông thường, ở các phương pháp phân tích khác trong Data mining, kiểm định chi bình phương thường xuất hiện và được ứng dụng ở bước kiểm tra mô hình, đánh giá giúp nhà phân tích mối quan hệ giữa các tham số đối với biến mục tiêu.
Kiểm định chi bình phương có thể được ứng dụng trong công việc hàng ngày ở các công ty để giải quyết các câu hỏi Yes/ No đơn giản về mối quan hệ giữa 2 yếu tố cần xem xét ví dụ kiểm tra mối liên hệ giữa các chương trình khuyến mãi với mức độ chi tiêu dùng của các khách hàng, mối liên hệ giữa lương thưởng và năng suất làm việc của nhân viên, mối liên hệ giữa các kênh chăm sóc khách hàng với mức độ hài lòng của khách,…
Lưu ý, mỗi yếu tố có thể chứa nhiều giá trị định danh khác nhau và không theo một các chuẩn nào cả, như ví dụ trên ở chỗ sản phẩm và thu nhập mỗi bên chỉ có 3 giá trị ứng với 3 nhóm.

Đến đây là kết thúc bài viết phần 1 về kiểm định phi tham số, sang bài viết phần 2 chúng ta sẽ tìm hiểu các dạng kiểm định tham số quan trọng như Sign – test, Wilcoxon – rank test, Mann – Whitney test, Kruskal – Wallis test.
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English