Quay trở lại với chủ đề Survival analysis – phân tích sống sót, ở bài viết phần 4 chúng ta đã cùng nhau tìm hiểu về phương pháp kiểm định Log – rank để so sánh, kiểm tra sự khác biệt trong tỷ lệ sống sót (Survival) giữa 2 hay nhiều đối tượng nghiên cứu, và đặc biệt là giới thiệu sơ lược về mô hình Cox Proportional Hazard Regression (gọi tắt Cox PH) là gì, bản chất, cấu trúc và thành phần.
Đến với bài viết phần 5, BigDataUni và các bạn sẽ đi qua các kiến thức quan trọng trước tiên trong mô hình Cox regression dạng đơn giản đầu tiên, thông qua ví dụ cụ thể, đó là Maximum likelihood estimation, Hazard ratio. Hi vọng qua các bài viết của chúng tôi, các bạn sẽ nắm được các khái niệm về phân tích sống sót, hỗ trợ quá trình nghiên cứu sâu hơn, và ứng dụng vào thực tế trong tương lai.

Dành cho các bạn chưa tham khảo các bài viết trước, lưu ý các thuật ngữ, phương pháp đã trình bày ở các phần trước chúng tôi sẽ không nhắc lại trong bài viết này:
Tìm hiểu Survival analysis (P.1): Khái niệm, ứng dụng
Tìm hiểu Survival analysis (P.2): Survival và Hazard Function
Tìm hiểu Survival analysis (P.3): Life table, Kaplan – Meier, Nelson -Aalen
Tìm hiểu Survival analysis (P.4): Log – rank và Cox PH (P.1)
Thay đổi một chút về cách tiếp cận trong trình bày các công thức Cox PH. Ở các bài viết trước nói về các phương pháp hồi quy (Regression), chúng tôi thường trình bày trước các công thức, sau đó rồi mới đến ví dụ diễn giải. Trong bài viết lần này về Cox PH, Survival analysis, BigDataUni sẽ giới thiệu trước ví dụ để các bạn lần nữa hiểu hơn về mục đích sử dụng Cox PH cũng như review lại một chút một số kiến thức trong Survival analysis.
Ví dụ mà chúng tôi sắp trình bày dưới đây là một ví dụ nổi tiếng, điển hình cho ứng dụng phân tích sống sót trong lĩnh vực y tế, cụ thể đánh giá các phương pháp điều trị cho những đối tượng bệnh nhân.
Chúng ta có bảng dữ liệu mẫu như sau:
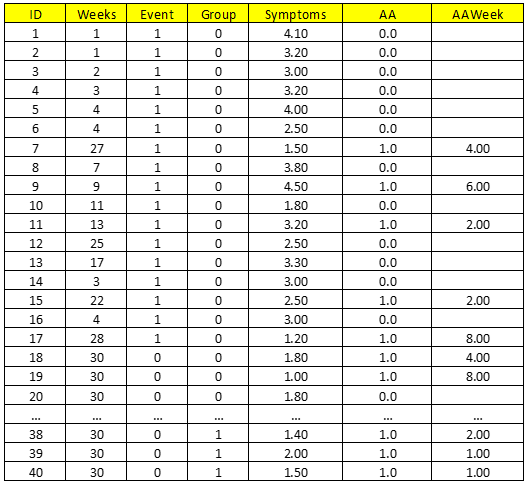
Dữ liệu tham khảo từ tài liệu nghiên cứu “Time and Change: Using Survival Analysis in Clinical Assessment and Treatment Evaluation” của 2 chuyên gia Douglas A. Luke và Sharon M. Homan từ đại học Y tế Công cộng Saint Louis. Dữ liệu là kết quả khảo sát từ một nghiên cứu về chủ đề lạm dụng thuốc, chất kích thích.
Tải dữ liệu mẫu tại đây: google drive
Mục đích của nghiên cứu là tìm hiểu khoảng thời gian bao lâu sau khi các bệnh nhân tiếp nhận điều trị chứng lạm dụng hay nghiện rượu sẽ “tái phạm” hay uống rượu trở lại, để đánh giá tính hiệu quả của phương pháp và phân tích sâu thêm các yếu tố khiến họ nghiện rượu trở lại.
Cột ID đầu tiên là thứ tự các bệnh nhân, Weeks = số tuần kể từ lúc bệnh nhân kết thúc điều trị cho đến lần đầu họ uống rượu trở lại, chúng ta coi việc họ uống rượu trở lại là một sự kiện thì Weeks là time – to – event hay Survival time. Survival = không uống rượu.
Event là sự kiện quan tâm đã hoặc chưa xảy ra, ở đây là việc bệnh nhân lần đầu uống rượu trở lại. giá trị bằng 1 tức đã xảy ra, 0 là chưa xảy ra. Giá trị 0 ở đây cũng được hiểu là trường hợp Censored: bệnh nhân bị mất dấu, quá trình kiểm tra, theo dõi bệnh nhân gặp vấn đề dẫn đến thiếu thông tin hoặc bệnh nhân kết thúc giai đoạn nghiên cứu (kéo dài tối đa 30 tuần) không uống rượu, và cần theo dõi thêm sau đó. Để hiểu hơn về Censored là gì các bạn xem lại bài viết phần 1, phần 2 nhé, link chúng tôi để ở đầu bài viết. Theo như mẫu dữ liệu, giá trị 0 xuất hiện ở các bệnh nhân theo dõi lần cuối là ở tuần thứ 30, tức không có trường hợp bị mất dấu bệnh nhân trong khoảng thời gian nghiên cứu. Censored ở ví dụ này mang tính tích cực, nghĩa là các bệnh nhân không uống rượu trong thời gian nghiên cứu và cần theo dõi thêm sau đó.
Group là nhóm bệnh nhân. Giá trị 0: các bệnh chỉ được áp dụng phương pháp “Detoxification” – phương pháp giải độc (phương pháp điều trị cho người nghiện rượu bằng cách kiêng đồ uống có cồn cho đến khi máu không còn chất độc). Giá trị 1: liệu pháp điều trị đầy đủ tại bệnh viện giải quyết vấn đề lạm dụng rượu.
Symptoms: là điểm trung bình từ kết quả kiểm tra tâm lý SCL – 10, thang đo từ 1 đến 5, điểm trung bình càng cao tức bệnh nhân có tâm lý không tốt, trong trạng thái lo âu, phiền muộn (Distress)
AA: giá trị 0: bệnh nhân chưa tham gia vào tổ chức Alcoholics Anonymous – tổ chức quốc tế hỗ trợ những người bị nghiện rượu. giá trị 1: đã tham gia vào tổ chức.
AAweek: tuần mà các bệnh nhân có buổi họp đầu tiên với tổ chức Alcoholics Anonymous sau khi tiếp nhận điều trị, cho biết bệnh nhân gia nhập vào tổ chức sớm hay trễ sau khi tiếp nhận điều trị. Giá trị thể hiện không phải là số tuần mà là thứ tự tuần. Ví dụ AAweek = 3, nghĩa là bệnh nhân tuần thứ 3 kể từ sau khi tiếp nhận điều trị, gia nhập vào Alcoholics Anonymous.
Chúng ta cùng nhìn qua đồ trị Survival function, và Hazard function, sử dụng phương pháp Kaplan – Meier trên SPSS
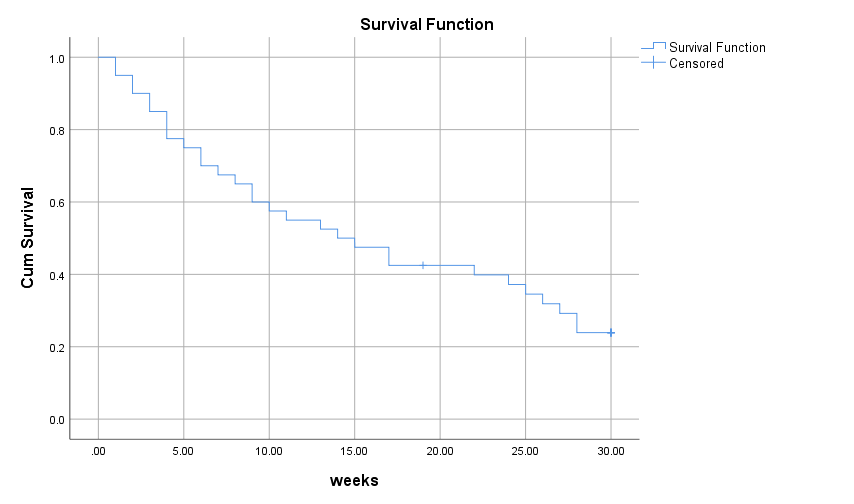
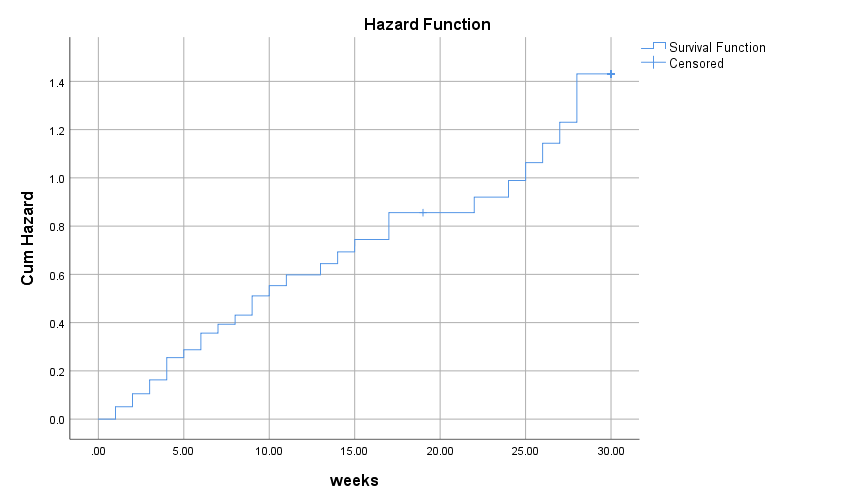
Kết quả cho thấy khi thời gian tăng thì khả năng hay nguy cơ các bệnh nhân bắt đầu uống rượu trở lại sẽ gia tăng.
So sánh tỷ lệ Survival giữa 2 nhóm bệnh nhân sử dụng phương pháp Detoxification và liệu trị lạm dụng tại bệnh viện
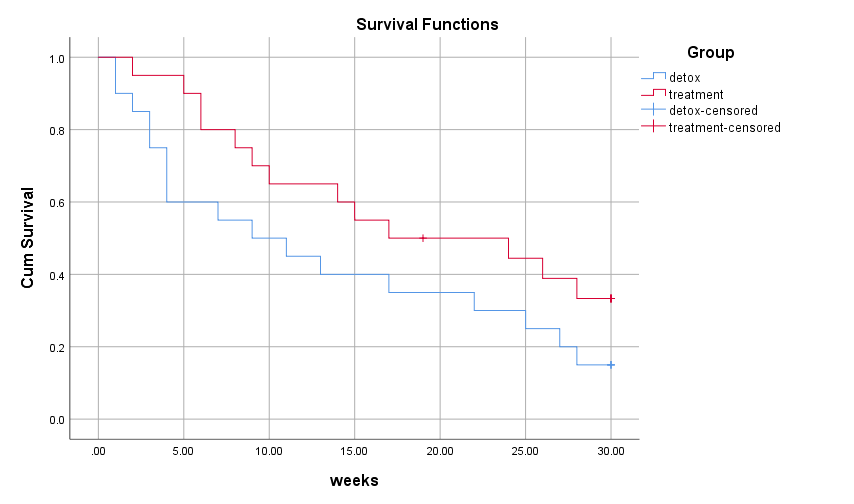

Chúng ta có thể thấy các bệnh nhân tiếp nhận phương pháp điều trị lạm dụng rượu cụ thể tại bệnh viện có kết quả tốt hơn các bệnh nhân sử dụng detoxification. Mặc dù kết quả Log – rank cho thấy tỷ lệ survival giữa 2 nhóm không có sự khác biệt khi giá trị kiểm định cho thấy không có ý nghĩa phân tích p – value = sig = 0.112 > 0.05 và cảnh báo chúng ta cần thêm dữ liệu để phân tích. Nhưng do đây là ví dụ nhỏ, và mẫu dữ liệu minh họa ít nên chúng ta tạm giả định rằng các chuyên gia đang quan tâm đến việc so sánh hiệu quả giữa 2 phương pháp và đưa Group vào mô hình Cox PH.
Tương tự so sánh giữa nhóm bệnh nhân tham gia và không tham gia tổ chức Alcoholics Anonymous
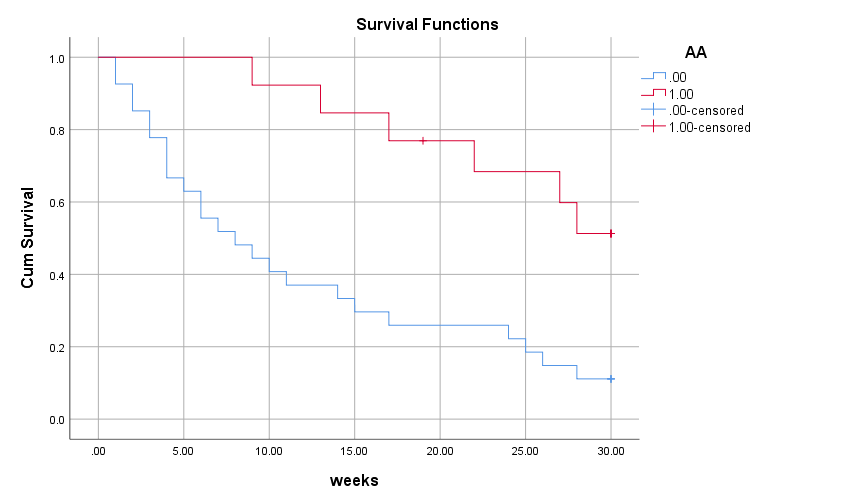

Kết quả khá rõ rệt các bệnh nhân tham gia tổ chức Alcoholic Anonymous có tỷ lệ không uống rượu trong 30 tuần kể từ lúc kết thúc điều trị cao hơn các bệnh nhân không tham gia. Kết quả kiểm định Log – rank có p-value = sig < 0.05, tức có sự khác biệt giữa 2 nhóm, chứng minh biến AA là biến có ý nghĩa phân tích và có thể đưa vào mô hình Cox PH.
Biến Symptons có giá trị định lượng, chúng ta có thể phân nhóm theo thang điểm để đánh giá. Ví dụ các bạn có thể phân nhóm như sau: nhóm 1 = thấp, các bệnh nhân có điểm trung bình từ 1 đến 2, nhóm 2 = trung bình, các bệnh nhân có điểm trung bình từ 2 đến 3, và nhóm 3 = cao các bệnh nhân có điểm trung bình từ 3 trở lên.
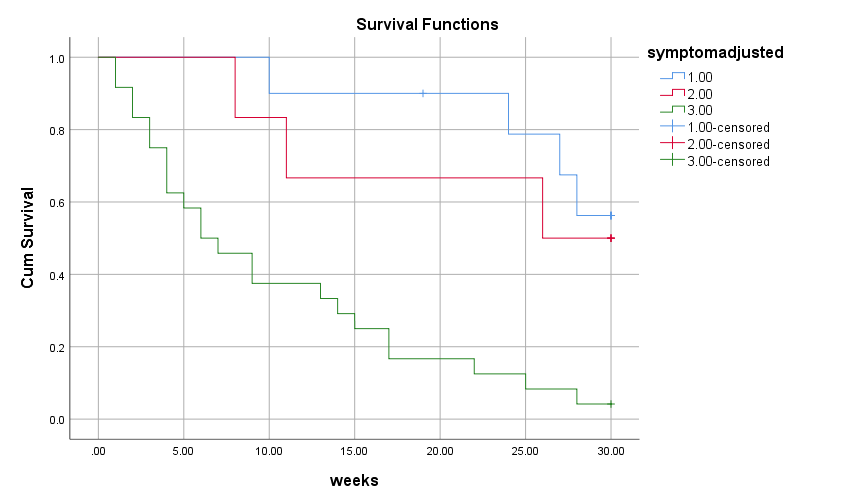
Kết quả chúng ta có thể thấy các bệnh nhân có điểm trung bình thấp, tức mức độ phiền muộn, lo âu thấp, tinh thần tốt, hiệu quả cai nghiện rượu sẽ tốt hơn các nhóm còn lại.
Như vậy chúng ta đã tìm hiểu tỷ lệ sống sót của các bệnh nhân giữa các yếu tố quan trọng, việc tiếp theo là xây dựng mô hình Cox PH. Dưới đây là kết quả từ SPSS
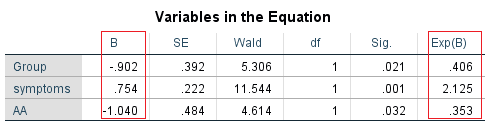

Theo bài viết trước chúng ta có phương trình tổng quát Cox PH:
h(t) = h0(t) * exp(β1X1 + β2X2 + … + βPXp)
Từ kết quả phân tích chúng ta thấy có 3 biến được đưa vô phương trình, tạm thời chúng ta chưa xét đến kết quả kiểm định log likehood, chi bình phương Chi – square, Wald – test, trong bài viết này chúng ta sẽ tìm hiểu β và exp (β) là gì thông qua 2 kiến thức quan trọng sắp được trình bày dưới đây.
Phương trình ước lượng tỷ lệ rủi ro bệnh nhân uống lại rượu được viết lại như sau:
h(t) = h0(t)*exp(-0.902X1 + 0.754X2 – 1.04X3
Các hệ số hồi quy trong Cox PH có nhiệm vụ giống như hệ số hồi quy trong các mô hình hồi quy bình thường, có vai trò định lượng mức tăng thêm hay giảm đi trong giá trị của biến mục tiêu khi các biết dự báo, biến X thay đổi 1 đơn vị.
Diễn giải hệ số hồi quy:
- Với hệ số hồi quy -0.902 ở biến group, nếu các bệnh nhân thuộc nhóm tiếp nhận điều trị lạm dụng rượu tại bệnh viện (có giá trị bằng 1 tại biến Group) mang lại hiệu quả tốt hơn với tỷ lệ uống rượu trở lại giảm e-0.902 – 1 = – 0.59 tức giảm 59% so với các nhóm bệnh nhân chỉ điều trị bằng Detoxification khi các yếu tố khác giữ nguyên không đổi.
- Với hệ số hồi quy 0.754 ở biến symtoms, nếu các bệnh nhân có kết quả trung bình kiểm tra tâm lý SCL – 10 tăng 1 đơn vị thì nguy cơ họ uống rượu trở lại tăng e0.754 – 1 = 1.125 tức tăng 112.5% khi các yếu tố khác giữ nguyên không đổi.
- Với hệ số hồi quy -1.04 ở biến AA, nếu các bệnh nhân sau khi tiếp nhận điều trị và có tham gia vào tổ chức Alcoholics Anonymous (có giá trị bằng 1 taị biến AA) thì nguy cơ uống rượu trở lại giảm e-1.04 – 1 = -0.64 tức giảm 64% so với nhóm bệnh nhân không tham gia khi các yếu tố khác giữ nguyên không đổi.
Cách nhận xét khác: ví dụ với hệ số hồi quy -0.902 ở biến group, nếu các bệnh nhân thuộc nhóm tiếp nhận điều trị lạm dụng rượu tại bệnh viện (có giá trị bằng 1) mang lại hiệu quả tốt hơn với tỷ lệ uống rượu trở lại nhỏ hơn e-0.902 = 0.406 lần chỉ điều trị bằng Detoxification khi các yếu tố khác giữ nguyên không đổi. Các bạn nhận xét tương tự với các biến còn lại
Như chúng tôi đã nói ở bài viết trước, cấu trúc của mô hình Cox PH được chia làm 2 phần chính là h0(t) và exp(βiXi) với h0(t) là đường baseline hazard function phụ thuộc vào thời gian, không chứa các biến X và không cần phải đưa ra các giả định hay phải tính toán, ước lượng nên chúng ta sẽ bỏ qua h0(t) và chỉ tập trung ước lượng phần exp(βiXi). ước lượng tác động của các biến X (có hay không phụ thuộc vào thời gian) lên tỷ lệ rủi ro Hazard
Các hệ số đầu tiên trong bảng kết quả Cox PH hay bất kỳ bảng kết quả phân tích hồi quy nào khác đều là hệ số hồi quy β. Vì tầm quan trọng và vai trò của chúng như đã nói ở trên, ước lượng tác động của các biến X. Vậy mô hình Cox PH sử dụng công thức gì để giúp chúng ta tìm ra các hệ số hồi quy này?
Maximum Likelihood Estimation (MLE)
Nếu bạn nào đã được học qua hồi quy Logistic thì chắc chắn đã nghe đến phương pháp này, đây là phương pháp được dùng để ước lượng hệ số hồi quy β trong hồi quy logistic.
MLE là phương pháp dự đoán tham số của một mô hình dựa trên những “quan sát” có sẵn (observed data), thông qua việc tìm kiếm một bộ những tham số/ hệ số hồi quy sao cho có thể tối đa hoá khả năng mà mô hình đó sinh ra các “quan sát” có sẵn.
Chúng tôi sẽ không trình bày lại MLE chi tiết ở đây mà chỉ trình bày công thức tổng quát diễn giải qua ví dụ cho các bạn dễ hiểu hơn khi nó được sử dụng trong MLE.
Các hệ số hồi quy trong ví dụ trên được ước tính theo hàm MLE ký hiệu là L từ chữ Likelihood hay L(β) với β là tập hợp các tham số chưa biết, đại diện cho các biến X.
Kết quả từ hàm MLE, L(β), là xác suất chung (joint probability) để các quan sát, đối tượng trong nghiên cứu đồng thời đạt những giá trị cụ thể tại biến mục tiêu (observed data) mà ở đây là tỷ lệ rủi ro với xác suất xảy ra đồng thời là cao nhất.
Khác với hồi quy logistic khi MLE xét cho tất cả các đối tượng nghiên cứu trong tập dữ liệu thì ở Cox PH, MLE chỉ được tính cho các đối tượng được ghi nhận là có sự kiện quan tâm xảy ra, như trong ví dụ này là các bệnh nhân quay trở lại uống rượu (event = 1), và không quan tâm đến những bệnh nhân nào là censored (event = 0) sẽ không được tính. Do đó L(β) còn gọi là “Partial Likelihood”
Công thức tổng quát như sau:
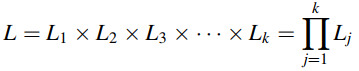
Lj là giá trị L, likelihood tại thời điểm xảy ra sự kiện lần thứ j với tập rủi ro cho trước (risk set) ký hiệu R(t(j))
Lj là khả năng sự kiện xảy ra ở thời điểm sự kiện lần thứ j với điều kiện các đối tượng nghiên cứu sống sót đến thời điểm đó hay sự kiện chưa xảy ra cho đến thời điểm đó. R(t(j)) là tập hợp các đối tượng nguy cơ tại thời điểm đang xét.
Ở trên chúng ta nói MLE trong Cox PH không quan tâm đến các đối tượng bị Censored tuy nhiên trong tập rủi ro sẽ bao gồm những đối tượng này cho dù chúng ta không biết trong tương lại họ có censored hay không. Các đối tượng Censored ở thời điểm sự kiện xảy ra lần thứ j ở ví dụ này là các đối tượng không uống rượu tính đến thời điểm đang xét, là thông tin đầu vào hữu ích để tính Lj
Sau khi xác định được biểu thức, hay phương trình L dựa trên dữ liệu có được, chúng ta sẽ phải tìm β sao cho giá trị Ln(L) là lớn nhất, bằng cách giải phương trình sau:
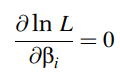
Quá trình được thực hiện bằng cách lấy đạo hàm riêng của log của L đối với từng tham số trong mô hình, được lặp lại nhiều lần sao cho đến khi các giá trị β tìm được thỏa mãn nhu cầu
Giới thiệu MLE để các bạn hiểu thêm về cách Cox PH dùng để ước tính các hệ số hồi quy. Thực tế các phần mềm phân tích, thống thê nổi tiếng như Stata, Minitab, SPSS,… đều tính giúp chúng ta một cách nhanh chóng và chính xác.
Chúng ta cùng qua ví dụ ngắn sau:
Giả sử chúng ta kiểm tra cùng lúc trong 3 bệnh nhân A, B, C (theo trình tự) xác định ai sẽ mắc Covid-19. Xác suất P sẽ bằng 1/6.
Khi kiểm tra bệnh nhân A, xác suất mắc bệnh 1/3. Sau đó loại bệnh nhân A ra, còn 2 bệnh nhân B, C, xác suất mắc bệnh khi xét đến bệnh nhân B là 1/2. Sau đó loại bệnh nhân B ra, còn duy nhất bệnh nhân C, xác suất mắc bệnh là 1/1.
P = 1/3 * 1/2 * 1/1 = 1/6
Như vậy khi tính xác suất xảy ra cùng lúc chúng ta sẽ dùng công thức nhân. Nó khác với trường hợp, chúng ta chọn ra 1 trong 3 bệnh nhân, p = 1/3. Các bạn thử nghĩ xem, trong thực tế, các bác sĩ có chọn ra bệnh nhân để xét nghiệm hay xét nghiệm tất cả? Khi cả 3 bệnh nhân đến, họ phải kiểm tra cả 3 cùng lúc giả sử khi họ biết 1 trong 3 người đã nhiễm bệnh trước đó, kiểm tra từng người, mỗi người 1 lần duy nhất, đã kiểm tra rồi thì không kiểm tra nữa.
Ví dụ trên chỉ minh họa để các bạn hiểu tại sao cần tính xác suất chung theo như trên.
Trong Survival analysis, khi nhận được một tập dữ liệu, chúng ta sẽ có thông tin chi tiết về thời gian, trạng thái và tiến hành tìm hiểu tỷ lệ rủi ro trung bình cho mỗi đối tượng trong nhóm các đối tượng được chỉ định theo dõi, hay gọi là nhóm nguy cơ, và xem xét toàn diện, chứ chúng ta không đi chọn ra ngẫu nhiên từng đối tượng, kiểm tra xong bỏ vô lại, rồi đi chọn tiếp.
Có thể có nhiều bạn chưa hiểu vì cách giải thích hơi dài dòng của chúng tôi, thì hãy cùng nhìn qua ví dụ khác sau
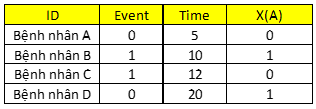
Giả sử chúng ta có 4 bệnh nhân, trong đó có 2 bệnh nhân bị nhiễm Covid được theo dõi trong quá trình cách ly, đó là 2 bệnh nhân B, C. Bên cạnh biến thời gian và biến sự kiện, chúng ta có thêm một biến X(A) khác, ví dụ biến này là loại đối tượng F1, trong 4 bệnh nhân có bệnh nhân B và D là F1.
Mô hình Cox PH được viết lại như sau:
h(t) = h0(t)*exp(β1X1) do có 1 biến X. Thay giá trị tại cột X(A) chúng ta có:
Bệnh nhân A: h(t) = h0(t)*exp(0)
Bệnh nhân B: h(t) = h0(t)*exp(β1)
Bệnh nhân C: h(t) = h0(t)*exp(0)
Bệnh nhân D: h(t) = h0(t)*exp(β1)
L = L1*L2 Vì có 2 sự kiện xảy ra ở bệnh nhân B, C, nên không tính L cho bệnh nhân A, D do 2 bệnh nhân này Censored
L1 = h0(t)*exp(β1)/ [h0(t)*exp(0) + h0(t)*exp(β1) + h0(t)*exp(0)], sự kiện xảy ra lần thứ 1 tại t1 = 10, lúc này còn 3 bệnh nhân trong risk set (do đã loại bỏ bệnh nhân A)
L2 = h0(t)* / [h0(t)*exp(0) + h0(t)*exp(β1)] sự kiện xảy ra lần thứ 2 tại t2 = 12, lúc này còn 2 bệnh nhân trong risk set (do đã loại bỏ bệnh nhân A, B)
- L = L1 * L2 = [exp(β1)/[ exp(0) + exp(β1) + exp(0)]] *[ exp(0)/ [exp(0) + exp(β1)]]
Từ phương trình trên cho thấy L không phụ thuộc vào h0(t). Do đó khi triển khai phân tích và tìm ra các hệ số hồi quy, xây dựng phương trình Cox PH, chúng ta không cần đi ước tính h0(t).
Để tìm được hệ số hồi quy cho biến X(A) chúng ta phải tìm β1 sao cho L đạt giá trị lớn nhất.
Tuy nhiên giả sử trường hợp, có 2 bệnh nhân cùng mắc Covid ở một mốc thời điểm, ví dụ cùng time = 12. Thì nên xử lý thế nào?
Nếu cùng mốc thời điểm, chúng ta vẫn biết ai mắc bệnh trước ví dụ bệnh nhân B mắc bệnh vào buổi sáng ngày thứ 12, còn bệnh nhân C mắc bệnh vào buổi chiều, thì cứ làm giống như trên.
Nhưng nếu không xác định được ai đến trước đến sau chúng ta sẽ phải xác định LBC và LCB tức tính cho cả 2 trường hợp B trước A sau và ngược lại, sau đó cộng lại Lt(12) = LBC + LCB rồi đưa vào lại L tính tiếp.
Đây là trường hợp theo tiếng Anh gọi là “Tied results/ failures”
Tóm lại, trong MLE các bạn chỉ cần biết cách thức vận hành của nó, để hiểu thêm về bản chất của Cox PH, và việc tính toán hãy để các phần mềm phân tích làm thay bạn, đừng quá căng thẳng khi thấy nó phức tạp!
Như vậy sau khi đã biết các hệ số hồi quy từ đâu mà ra, chúng ta cùng đến với exp(β), nó mang ý nghĩa gì?
Hazard ratio
Đáng lẽ chúng ta phải nói phần này trước cả phần MLE hay hệ số hồi quy, vì Hazard ratio là động cơ để chúng ta diễn giải hệ số hồi quy, là cơ sở để định lượng ảnh hưởng của các yếu tố tác động lên tỷ lệ rủi ro của các đối tượng nghiên cứu.
Trong hồi quy Logistic, chúng ta đã được học qua Odds Ratio, so sánh xác suất xảy ra sự kiện quan tâm giữa 2 nhóm, một nhóm sẽ có giá trị ở biến X nào đó hơn nhóm kia 1 đơn vị.
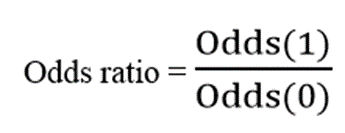
Odds ratio là tỷ lệ của 2 odds đo lường tác động của một biến độc lập lên odds (odds là khả năng sự kiện quan tâm xảy ra, y = 1) khi giá trị của biến này thay đổi 1 đơn vị, và các biến còn lại được giữ nguyên. Dễ hiểu hơn, chúng ta có odds(1) của y = 1 (là xác suất p để y = 1 chia cho (1 – p) khi một biến độc lập thay đổi 1 đơn vị) chia cho odds(0) của y = 1 (là xác suất p để y = 1 chia cho (1 – p) khi giá trị của các biến độc lập giữ nguyên không thay đổi)
Với y là biến mục tiêu trong hồi quy Logistic, có 2 giá trị 0 hoặc 1.
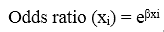
Bên trên là công thức thể hiện mối quan hệ giữa Odds ratio của mỗi biến và hệ số hồi quy β. Các bạn có thấy quen không? Hãy nhìn lại phần trên, chỗ chúng tôi diễn giải về các hệ số β trong ví dụ ban đầu, các bạn sẽ thấy được điểm giống nhau.
Quay trở lại với Hazard ratio (ký hiệu HR), với cách vận hành gần giống Odds ratio. Nếu Odds ratio dùng để so sánh xác suất sự kiện xảy ra giữa 2 nhóm, thì Hazard ratio dùng để so sánh tỷ lệ rủi ro xảy ra sự kiện giữa 2 nhóm. Điểm khác biệt, odds ratio dùng odds tức p, xác suất để so sánh, p có giá trị từ 0 đến 1.
Còn Hazard ratio sử dụng tỷ lệ hazard. Mà như đã được giới thiệu ở các bài viết trước, tỷ lệ hazard không phải xác suất, có thể lớn hơn 1. Ví dụ một loại máy móc sản xuất có tỷ lệ rủi ro mắc lỗi 2/ ngày, tức nguyên 1 ngày có thể mắc 2 lỗi.
Công thức của Hazard ratio:
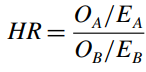
OA, OB là số đối tượng thuộc nhóm A, B trải qua sự kiện được quan tâm, EA, EB là số đối tượng có nguy cơ (mong đợi) đối mặt với sự kiện được quan tâm. Ví dụ ở trên, các bệnh nhân có X(A) = 1 sẽ đưa vào nhóm A, còn lại sẽ đưa vào nhóm B.
Chúng ta có EA = 2, EB = 2, OA = 1, OB = 1. HR = 1. Tỷ lệ rủi ro mắc Covid của 2 nhóm bệnh nhân là như nhau. Biến X(A) không có ảnh hưởng lên tỷ lệ rủi ro.
Đó là cách hiểu đơn giản về tìm hiểu tác động của các biến hay yếu tố lên tỷ lệ rủi ro thông qua Hazard ratio. Công thức ở trên chúng ta dùng tỷ lệ nên loại bỏ được yếu tố thời gian.
Trong Cox PH, Hazard ratio dùng để so sánh 2 mô hình với một mô hình chứa biến cần xét và mô hình còn lại không chứa biến cần xét hoặc hiểu cách khác, một nhóm có giá trị tại biến đang xét lớn hơn nhóm còn lại cũng có biến đó là 1 đơn vị. hay so sánh 2 nhóm phân biệt bởi giá trị của biến cần xét.
Lưu ý, chúng tôi dùng Hazard ratio, giữ nguyên thuật ngữ, không dịch sang tiếng Việt để tránh nhầm lẫn với tỷ lệ rủi ro h(t), biến mục tiêu trong phương trình Cox PH
Ví dụ chúng ta có biến giời tính 0: nữ, 1: nam
HR = [h0(t)*exp(β*Xnam)]/ [h0(t)* exp(β*Xnữ)] = [h0(t)*exp(β*Xnam)]/ [h0(t)*exp(β*Xnữ)] = [exp(β*1)]/ [exp(β*0)] = exp(β) = eβ
- HR = h(t)nam/ h(t)nữ = eβ giới tính
Đến đây chắc các bạn cũng hiểu được cách chúng ta diễn giải các hệ số hồi quy ở đầu bài viết.
Giả sử chúng ta có mô hình ban đầu chỉ với 1 biến, X(A), sau đó chúng ta thêm một biến X(M) khác giống như một yếu tố khác thêm vào (có giá trị 0 = không có tác động của X(M) và 1 = có tác động của X(M)), và xem ảnh hưởng của nó lên đối tượng nghiên cứu mà trước đó đã có X(A).
HR = [h0(t)*exp(βA*X(A) + βM*X(M))]/ [h0(t)* exp(βA*X(A) + βM*X(M))] = exp(βA*1 + βM*1)/ exp(βA*1 + βM * 0) = exp(βA + βM – βA) theo công thức log
- HR = exp(βM) = eβM = HRX(M)
Đây là giải thích cho việc tại sao ở mỗi biến chúng ta đều có Hazard Ratio
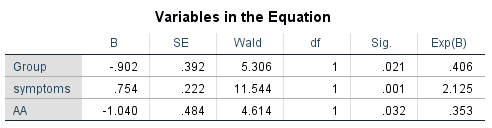
Ở mỗi biến đều có giá trị ở cột Exp (β) tức, Hazard ratio.
Ví dụ, HRGroup = exp(-0.902) = 0.406. Nếu các bệnh nhân thuộc nhóm tiếp nhận điều trị lạm dụng rượu tại bệnh viện (có giá trị bằng 1) mang lại hiệu quả tốt hơn với tỷ lệ uống rượu trở lại nhỏ hơn 0.406 lần so với nhóm chỉ tiếp nhận Detoxification.
Chúng ta đã nói quá nhiều về Hazard ratio và giá trị 0, 1. Giả sử chúng ta muốn tìm hiểu sự khác biệt trong tỷ lệ HR nếu 2 nhóm bất kỳ mang những giá trị khác nhau, cụ thể hơn, ngoài 0 và 1 ở các biến, đặc biệt là biến định lượng?
Ví dụ chúng ta có biến Symptoms là biến định lượng (có thể là biến thứ bậc) có giá trị lớn hơn 0, 1
HR = h(t)(Symptoms = A1)/ h(t)(Symptoms = A2) = exp(βSymptonsA1)/ exp(βSymptonsA2)
= exp (βSymptons*(A1 – A2))
Ví dụ so sánh tỷ lệ rủi ro giữa bệnh nhân có điểm kiểm tra SCL – 10 là 2.5 và một bệnh nhân khác là 3.7
HR = exp(0.754*(2.5 – 3.7)) = 0.404
Tức bệnh nhân có điểm đo lường mức độ phiền muộn là 2.5 sẽ có tỷ lệ rủi ro uống rượu trở lại nhỏ hơn 0.4 lần so với bệnh nhân có điểm 3.7,
Hay (1 – 0.4) = 0.6, tức giảm 60% so với bệnh nhân có điểm 3.7.
Đó là chúng ta muốn tìm hiểu thêm trong mỗi biến, trong thực tế để mô tả chung nhất tác động của biến lên tỷ lệ rủi ro, các chuyên gia thường sử dụng “1 đơn vị” để làm thước đo đánh giá 2 mô hình. Một mô hình chứa biến cần xét (giá trị x = 1 nhân hệ số β) và mô hình còn lại không chứa biến (giá trị x = 0 nhân hệ số β)
Một lý do khác đó chính là nhấn mạnh giả định Hazard ratio của mỗi biến không đổi theo thời gian.
Khi A1 – A2 = 1 ở bất kỳ giá trị A1, A2 nào. Hazard ratio sẽ luôn bằng Exp (β)
Các giả định khác đó là:
- Thời điểm xảy ra sự kiện hay Survival time giữa mỗi đối tượng trong tập dữ liệu là khác biệt nhau, độc lập với nhau.
- Tỷ lệ rủi ro h(t) chịu tác động từ các biến X độc lập với nhau, và không có mối quan hệ với thời gian. Tức ở phần eβiXi các biến X không có liên quan đến thời gian.
- Nếu Cox PH sử dụng exponential regression, thì h0(t) hay còn gọi Baseline hazard function (đường Hazard cơ sở ) sẽ giữ nguyên, không đổi theo thời gian.
- Mối quan hệ giữa các biến dự báo X, và đường Hazard cơ sở là mối quan hệ thể hiện qua phép toán nhân (Multiplicative relationship)
Trước khi kết thúc bài viết lần này, chúng ta cùng xem qua cách sử dụng Hazard ratio để đánh giá tác động của biến dự báo lên tỷ lệ rủi ro:
Giả sử chúng ta có 2 nhóm so sánh, 1 nhóm chứa biến đang xét và 1 nhóm không chứa biến đang xét
- HR = 1; không có sự khác biệt giữa tỷ lệ rủi ro giữa 2 nhóm so sánh, biến đầu vào đang xét không có tác động lên nguy cơ xảy ra sự kiện
- HR > 1: có sự khác biệt giữa tỷ lệ rủi ro giữa 2 nhóm so sánh, giá trị của biến đầu vào đang xét tăng lên, sẽ khiến nguy cơ xảy ra sự kiện tăng theo.
- HR < 1: có sự khác biệt giữa tỷ lệ rủi ro giữa 2 nhóm so sánh, giá trị của biến đầu vào đang xét tăng lên, sẽ khiến nguy cơ xảy ra sự kiện giảm xuống
Đến đây là kết thúc bài viết. Hẹn gặp lại các bạn ở các bài viết sắp tới.
Tài liệu tham khảo:
Tài liệu nghiên cứu “Time and Change: Using Survival Analysis in Clinical Assessment and Treatment Evaluation” của 2 chuyên gia Douglas A. Luke và Sharon M. Homan
“Survival Analysis” – Lisa Sullivan
“An Introduction to Survival Analysis” – Mario Cleves và cộng sự
“Survival Analysis A Practical Approach” – David Machin và cộng sự
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English