Quay trở lại với chủ đề Survival analysis, phương pháp phân tích sống sót trong Data mining. Ở bài viết trước, chúng ta đã đi vào tìm hiểu hệ số hồi quy β, Hazard ratio bao gồm khái niệm, ý nghĩa và phương pháp tính, cũng như phân tích mối quan hệ giữa chúng. Tiếp tục phần 3 của mô hình Cox Proportional Hazard Regression (Cox PH), và là bài viết cuối cùng của Survival analysis, BigDataUni và các bạn sẽ tiếp tục đi qua các công thức, số liệu quan trọng khác cần quan tâm trong Cox PH.

Dành cho các bạn chưa tham khảo các bài viết trước, lưu ý các thuật ngữ, phương pháp đã trình bày ở các phần trước chúng tôi sẽ không nhắc lại trong bài viết này:
Tìm hiểu Survival analysis (P.1): Khái niệm, ứng dụng
Tìm hiểu Survival analysis (P.2): Survival và Hazard Function
Tìm hiểu Survival analysis (P.3): Life table, Kaplan – Meier, Nelson -Aalen
Tìm hiểu Survival analysis (P.4): Log – rank và sơ lược Cox PH
Tìm hiểu Survival analysis (P.5): Hệ số hồi quy và Hazard ratio trong Cox PH
Nhắc lại một chút, mô hình Cox PH regression ước tính tỷ lệ rủi ro có phương trình tổng quát:
h(t) = h0(t) * exp(β1X1 + β2X2 + … + βPXp)
sẽ có 2 phần chính:
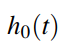
Và:
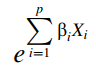
Với h0(t) được gọi là Baseline Hazard function, hàm Hazard theo thời gian hay đường Hazard cơ sở theo thời gian. Ở phần thứ hai, hàm mũ e, các biến X độc lập với thời gian đại diện cho các yếu tố tác động lên tỷ lệ rủi ro h(t) được định lượng bởi các hệ số hồi quy β. Sử dụng Cox PH chúng ta không cần đưa ra bất kỳ giả định gì về quy luật phân phối, hay không phải xác định bất kỳ tham số, cũng như mô hình nào cho nó, đặc biệt là không cần ước lượng h0(t), chỉ tập trung xây dựng model trên phần thứ 2
Quay trở lại với ví dụ mà chúng ta đang nói dở ở bài viết phần 5.
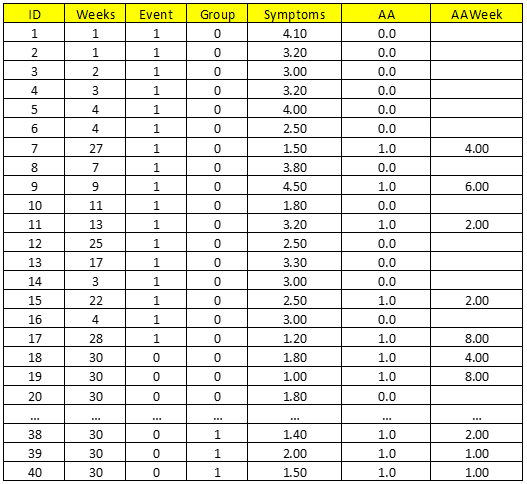
Dữ liệu tham khảo từ tài liệu nghiên cứu “Time and Change: Using Survival Analysis in Clinical Assessment and Treatment Evaluation” của 2 chuyên gia Douglas A. Luke và Sharon M. Homan từ đại học Y tế Công cộng Saint Louis. Dữ liệu là kết quả khảo sát từ một nghiên cứu về chủ đề lạm dụng thuốc, chất kích thích để tìm hiểu khoảng thời gian bao lâu sau khi các bệnh nhân tiếp nhận điều trị chứng lạm dụng hay nghiện rượu sẽ “tái phạm” hay uống rượu trở lại, để đánh giá tính hiệu quả của phương pháp và phân tích sâu thêm các yếu tố khiến họ nghiện rượu trở lại.
Tải dữ liệu mẫu tại đây: google drive
Cột ID đầu tiên là thứ tự các bệnh nhân, Weeks = số tuần kể từ lúc bệnh nhân kết thúc điều trị cho đến lần đầu họ uống rượu trở lại, chúng ta coi việc họ uống rượu trở lại là một sự kiện thì Weeks là time – to – event hay Survival time. Survival = không uống rượu.
Event là sự kiện quan tâm đã hoặc chưa xảy ra, ở đây là việc bệnh nhân lần đầu uống rượu trở lại. giá trị bằng 1 tức đã xảy ra, 0 là chưa xảy ra. Giá trị 0 ở đây cũng được hiểu là trường hợp Censored: bệnh nhân bị mất dấu, quá trình kiểm tra, theo dõi bệnh nhân gặp vấn đề dẫn đến thiếu thông tin hoặc bệnh nhân kết thúc giai đoạn nghiên cứu (kéo dài tối đa 30 tuần) không uống rượu, và cần theo dõi thêm sau đó.
Group là nhóm bệnh nhân. Giá trị 0: các bệnh chỉ được áp dụng phương pháp “Detoxification” – phương pháp giải độc. Giá trị 1: liệu pháp điều trị đầy đủ tại bệnh viện giải quyết vấn đề lạm dụng rượu.
Symptoms: là điểm trung bình từ kết quả kiểm tra tâm lý SCL – 10, thang đo từ 1 đến 5, điểm trung bình càng cao tức bệnh nhân có tâm lý không tốt, trong trạng thái lo âu, phiền muộn (Distress)
AA: giá trị 0: bệnh nhân chưa tham gia vào tổ chức Alcoholics Anonymous – tổ chức quốc tế hỗ trợ những người bị nghiện rượu. giá trị 1: đã tham gia vào tổ chức.
AAweek: tuần mà các bệnh nhân có buổi họp đầu tiên với tổ chức Alcoholics Anonymous sau khi tiếp nhận điều trị, cho biết bệnh nhân gia nhập vào tổ chức sớm hay trễ sau khi tiếp nhận điều trị. Giá trị thể hiện không phải là số tuần mà là thứ tự tuần.
Ở bài viết trước chúng ta đã thực hiện xây dựng mô hình Cox PH cho ví dụ trên sử dụng SPSS.

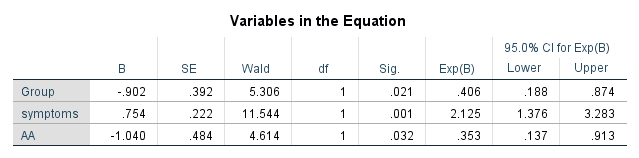
Phương trình tổng quát Cox PH
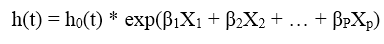
- h(t) = h0(t)*exp(-0.902X1 + 0.754X2 – 1.04X3)
Các bạn xem lại bài viết phần 5 để hiểu về Hazard ratiom hệ số hồi quy (chúng tôi không trình bày lại ở bài viết này), cách sử dụng chúng để mô tả tác động của các yếu tố lên tỷ lệ rủi ro thông qua công thức tính mối quan hệ giữa chúng.
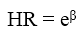
Standard Error
Chúng ta đã biết được hệ số hồi quy, Hazard ratio = exp (β) là gì. Số liệu cần quan tâm tiếp theo trong bảng là SE hay Standard Error, sai số chuẩn của các hệ số hồi quy.
Nếu bạn nào học qua thống kê thống kê chắc cũng biết đến sai số chuẩn. Thông thường trong thực tế, chúng ta khó có thể xác định được tất cả các đối tượng của tổng thể nghiên cứu. Đó là lý do chúng ta phải ứng dụng các phương pháp chọn mẫu từ tổng thể
Tuy nhiên không phải mẫu nào cũng giống nhau hoàn toàn, và cũng không phải mẫu nào thể hiện đúng tất cả các tính chất, đặc điểm đại diện cho tổng thể.
Như vậy khi chúng ta chọn ra N mẫu có n số đối tượng, chúng ta sẽ có N số liệu đặc trưng cho tổng thể, ví dụ như N số trung bình. Câu hỏi đặt ra là nếu chọn mẫu nhiều lần (“nhiều” ở đây có có thể lên đến hàng triệu hay tỉ lần) thì các số trung bình này dao động cỡ nào? Hay nói cách khác số trung bình sẽ biến thiên như thế nào từ mẫu này sang mẫu khác? Sai số chuẩn sẽ cho chúng ta biết được điều này. Sai số chuẩn chính là độ lệch chuẩn (Standard deviation) của N số trung bình.
Trở lại với ví dụ ở trên, giả sử bệnh viện tiến hành cuộc thử nghiệm trên nhiều nhóm đối tượng được chọn ngẫu nhiên trong một thành phố, thì họ cũng sẽ có nhiều hệ số hồi quy ứng với mỗi biến. Sai số chuẩn càng nhỏ cho thấy hệ số hồi quy đang xét định lượng chính xác nhất tác động của biến hay yếu tố đó trong thực tế lên tỷ lệ rủi ro.
Công thức, cách tính sai số chuẩn của các hệ số hồi quy trong mô hình Cox PH khá phức tạp nên chúng tôi sẽ không đề cập trong bài viết này. Các bạn quan tâm có thể tìm hiểu ở những tài liệu khác.
Trong tất cả các phần mềm phân tích, phần mềm thống kê như SPSS, Minitab, Stata,… đều tính sẵn sai số chuẩn cho chúng ta. Việc của chúng ta là tìm ra mô hình Cox PH phù hợp nhất cho tập dữ liệu.
Việc so sánh các mô hình Cox PH dựa trên sai số chuẩn phụ thuộc vào cách chúng ta thiết kế nghiên cứu và chọn mẫu, liên quan đến quy luật phân phối mẫu. Nếu 2 mẫu hay tập dữ liệu khác nhau về cách chọn mẫu (ví dụ một cái chọn mẫu ngẫu nhiên, một cái không ngẫu nhiên), khác nhau về số lượng quan sát trong mẫu thì không nên sử dụng SE làm thước đo độ hiệu quả của các mô hình tìm được. Thay vào đó các chuyên gia thường kết hợp SE vào các chỉ số đo lường khác mà chúng tôi sắp trình bày dưới đây để đưa ra những đánh giá đúng hơn cho mô hình Cox PH.
Confidence Interval của Hazard ratio hay Exp(β)
Điều chúng ta quan tâm khi tiến hành xây dựng mô hình Cox PH chính là tìm hiểu tỷ lệ rủi ro, nguy cơ xảy ra sự kiện sẽ bị tác động bởi những yếu tố khác như thế nào thông qua hệ số hồi quy và đặc biệt là Hazard ratio.
Tuy nhiên Hazard ratio mà chúng ta tìm được trong bảng kết quả chỉ mới ước lượng từ một mẫu dữ liệu, nếu sử dụng các số liệu Hazard ratio trong bảng để đưa ra kết luận trong thực tế thì có thể không đúng, có sai số. Thế nhưng chúng ta cũng không biết chính xác Hazard ratio thực tế của tổng thể nghiên cứu là bao nhiêu, mà chỉ có thể ước lượng khoảng và khẳng định nó sẽ nằm trong khoảng đó với độ tin cậy là bao nhiêu phần trăm.
Trong thống kê, chúng ta biết đến ước lượng khoảng tin cậy cho các tham số của tổng thể sử dụng trung bình mẫu, tỷ lệ mẫu.
Công thức ước lượng thường sử dụng trong thống kê:
Với µ là trung bình tổng thể, x– là trung bình mẫu, tìm khoảng tin cậy có chứa µ

Viết lại công thức theo sai số chuẩn (SE)

Với:

Từ đó suy ra công thức ước lượng cho hệ số hồi quy

Sai số chuẩn của hệ số hồi quy chúng ta lấy từ bảng kết quả của các phần mềm phân tích, thường ở cột kế bên cột hệ số hồi quy.
Zα/2 là giá trị tra bảng phân phối Z, với mức ý nghĩa α thường mặc định là 0.05, độ tin cậy = 1 – 0.05 = 95%.
Vì chúng ta sử dụng Hazard ratio để phân tích tác động, thay vì β nên công thức trên sẽ viết lại:

Ví dụ, ở biến Group, nhóm bệnh nhân, chúng ta có hệ số hồi quy β = -0.902, SE = 0.392, với α = 0.05, Z0.025 = 1.96 (tra bảng Z với giá trị 1 – 0.025 = 0.975)
*Lưu ý, bạn nào chưa học qua thống kê có thể sẽ không hiểu phần này. Các bạn có thể tham khảo lại các bài viết về thống kê, kiểm định của chúng tôi trong mục Blog.
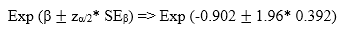
HR nằm trong khoảng (exp(-1.670332); exp(-0.13368)) = (0.188; 0.874)

Các bạn xem ở cột 95% CI for Exp (β), lower là giá trị chặn dưới, Upper là giá trị chặn trên.
Kết luận: trong thực tế, nếu các bệnh nhân thuộc nhóm tiếp nhận điều trị lạm dụng rượu tại bệnh viện (có giá trị bằng 1) mang lại hiệu quả tốt hơn với tỷ lệ uống rượu trở lại nhỏ hơn nằm trong khoảng từ 0.188 đến 0.874 lần so với nhóm chỉ tiếp nhận Detoxification, với độ tin cậy 95%.
Các bạn thử làm tương tự với 2 biến còn lại là Symtoms và AA.
Tiếp tục, mục đích khác của việc xác định khoảng tin cậy chính là kiểm tra liệu biến hay yếu tố đang xét có tác động lên biến mục tiêu hay không.
Các chuyên gia phân tích thường quan tâm mục đích này hơn cả việc tính toán khoảng tin cậy, vì nếu thông qua khoảng tin cậy, có dấu hiệu biến đang xét khả năng không có tác động lên tỷ lệ rủi ro h(t) trong mô hình Cox PH, thì chúng sẽ không có ý nghĩa phân tích tiếp.
Quay trở lại với Hazard ratio, ở cuối bài viết trước (P.5) chúng tôi có đề cập cách sử dụng Hazard ratio để đánh giá tác động của biến dự báo lên tỷ lệ rủi ro:
Giả sử chúng ta có 2 nhóm so sánh, 1 nhóm chứa biến đang xét và 1 nhóm không chứa biến đang xét
- HR = 1; không có sự khác biệt giữa tỷ lệ rủi ro giữa 2 nhóm so sánh, biến đầu vào đang xét không có tác động lên nguy cơ xảy ra sự kiện
- HR > 1: có sự khác biệt giữa tỷ lệ rủi ro giữa 2 nhóm so sánh, giá trị của biến đầu vào đang xét tăng lên, sẽ khiến nguy cơ xảy ra sự kiện tăng theo.
- HR < 1: có sự khác biệt giữa tỷ lệ rủi ro giữa 2 nhóm so sánh, giá trị của biến đầu vào đang xét tăng lên, sẽ khiến nguy cơ xảy ra sự kiện giảm xuống.
Như vậy, nếu HR = 1, thì yếu tố hay biến đang xét sẽ không có ý nghĩa khi đưa vào mô hình.
Ở biến Group chúng ta có khoảng tin cậy cho HR (0.188; 0.874), HR = 1 sẽ không nằm trong khoảng này, do HR = 1 > 0.874 > 0.188. Như vậy biến Group ban đầu có thể đánh giá là có ý nghĩa phân tích khi nó có ảnh hưởng lên tỷ lệ bệnh nhân uống rượu lại (tỷ lệ rủi ro sự kiện xảy ra)
Ở biến Symtoms, và biến AA, cũng như vậy giá trị HR = 1 đều nằm ngoài khoảng tin cậy tức sẽ không có khả năng HR của mỗi biến bằng 1. Trên cơ sở đó, chúng ta kết luận tương tự như biến Group.
Để chắc chắn, các biến X đầu vào có ý nghĩa phân tích, chúng ta cần sử dụng thêm phương pháp kiểm định khác còn được gọi là Wald test.
Wald test
Nếu các bạn đã được học qua hồi quy tuyến tính và hồi quy Logistic, có thể đã biết đến kiểm định t và kiểm định Wald được dùng để kiểm định có hay không có mối quan hệ giữa từng biến độc lập và biến mục tiêu. Công thức Wald test cũng được áp dụng trong mô hình Cox PH
Với β = 0, HR = exp (0) = 1nghĩa là biến độc lập X và biến mục tiêu h(t) trong Cox PH không có mối quan hệ với nhau.
Chúng ta có thể đặt các giả thuyết như sau:
H0: β = 0
H1: β ≠ 0
Công thức kiểm định:

Trong một số phần mềm thống kê thì W2 = Z2 , tức bình phương tỷ số ở trên với cơ sở giả thuyết H0 tuân theo phân phối chi bình phương, với bậc tự do là 1 nếu xét cho từng biến độc lập.

Cơ sở để bác bỏ giả thuyết H0 chúng ta có thể dựa trên kết quả tra bảng và kết quả kiểm định, nếu kết quả kiểm định > kết quả tra bảng, ngoài ra cũng dựa vào p-value để xét. Nếu xét trên giá trị p-value, bác bỏ H0 khi p-value < α. (p-value là mức ý nghĩa nhỏ nhất mà tại đó H0 bị bác bỏ).
Chúng ta trở lại với ví dụ ở trên:
Zgroup = – 0.902/ 0.392 = -2.3
- Z2 group = 5.3
Kết quả giống ở cột Wald-test ở trên bảng. Z tra bảng phân phối chi bình phương, α = 0.05, df = 1, bằng 3.84 < giá trị kiểm định 5.3. Suy ra bác bỏ H0, biến group có ý nghĩa phân tích, nó có quan hệ, có tác động với biến mục tiêu ở đây là tỷ lệ rủi ro bệnh nhân uống rượu trở lại. P-value = sig = 0.021 < 0.05 cũng cố thêm kết luận.
Theo kết quả từ SPSS, cả 3 biến đều có P-value < 0.05, cả 3 biến đều có tác động lên tỷ lệ rủi ro, và thích hợp để đưa vào mô hình.
Likelihood Ratio test
Likelihood Ratio Test (LR), một dạng kiểm định dựa trên so sánh 2 mô hình để xác định một hay các biến độc lập x có phù hợp đưa vào phân tích hay không, gồm một mô hình từ phương trình hồi quy tìm được có các biến được chọn lọc, và mô hình còn lại đầy đủ, nói cách khác là một mô hình sẽ là “tập con” của mô hình còn lại.
LR test là phương pháp kiểm tra mức độ “fit” của các mô hình Cox PH. “Fit” được hiểu như thế nào? Chúng ta đã biết việc xác định các hệ số hồi quy trong Cox PH hay logistic regression dựa trên Maximum Likelihood Estimation. MLE là phương pháp dự đoán tham số của một mô hình dựa trên những “quan sát” có sẵn, bằng cách tìm bộ tham số sao cho có thể tối đa hoá khả năng mà mô hình với bộ tham số đó sinh ra các “quan sát” có sẵn.
Như vậy likelihood hay log likelihood càng cao (càng tiến gần 0, do likelihood được đưa vào hàm log, luôn mang giá trị âm) thì chứng tỏ mô hình với các hệ số hồi quy đó sẽ mang lại hiệu quả phân tích. Một mô hình càng ít biến X, hay biến dự báo, thì log – likelihood sẽ thấp (tiến xa 0). Tuy nhiên, nếu chỉ dựa vào log – likelihood mà chọn lựa mô hình thì chưa thể khẳng định được một cách chắc chắn, thay vào đó chúng ta phải sử dụng LR
LR còn có thể đánh giá toàn bộ mô hình bao gồm tất cả các biến độc lập x hoặc chỉ đánh giá một biến độc lập x mà thôi. Với đánh giá 1 biến độc lập có ý nghĩa phân tích hay không, LR sẽ hướng đến so sánh giữa một mô hình không chứa biến đó và một mô hình chứa biến đó.
Trường hợp chúng ta đang xét một biến thì Likelihood ratio có công thức như sau:

Với L0 là likelihood của mô hình không chứa biến cần xét với hệ số hồi quy của biến đó bằng 0, L1 là likelihood của mô hình chứa biến cần xét với H0: mô hình L0 phù hợp
Trường hợp chúng ta có trên 2 biến độc lập đang xét, chúng ta sẽ so sánh mô hình một là mô hình không có 2 biến đó gọi là mô hình con (subset), với mô hình 2 là mô hình đầy đủ có chứa 2 biến đó (full). Với giả thuyết H0 mô hình subset là phù hợp.

Trường hợp chúng ta đánh giá tổng thể mô hình hiện tại bao gồm các biến độc lập và hệ số hồi quy xác định được từ phương trình tìm được (có thể gọi là reduced/ fitted/ current model). Chúng ta sẽ so sánh với mô hình “đầy đủ nhất” tức mô hình này sẽ bao gồm tất cả các biến độc lập và tất cả mối quan hệ giữa các biến độc lập với tất cả hệ số hồi quy tương ứng gọi là Saturated model, trong mô hình này giá trị dự báo sẽ tiến gần bằng giá trị thực tế.

Tủy thuộc vào loại mô hình chúng ta sẽ thường có cách gọi khác nhau nhưng cùng chung cách đặt giả thuyết là H0: mô hình L0/ Lsubset/ Lreduced không phù hợp.
Likelihood ratio được giả định xấp xỉ phân phối chi bình phương χ2 (Chi-squared distribution), -2 ở đầu công thức được đưa vào để điều chỉnh quy luật phân phối xấp xỉ theo phân phối chi bình phương.
Như vậy các kết quả đạt được từ những trường hợp trên chúng ta có thể ra bảng phân phối chi bình phương hoặc tìm ra p – value sử dụng phần mềm thống kê để kết luận bác bỏ hay không bác bỏ các giả thuyết H0 và kết luận mô hình nào phù hợp hay biến đã xét có thích hợp đưa vô mô hình không. Bậc tự do (degrees of freedom) chính là số chênh lệch trong tổng số biến độc lập của 2 mô hình. Lưu ý kết quả Log likelihood các bạn có thể tìm thấy khi sử dụng các phần mềm phân tích mà không phải tự tính tay, vì nó rất phức tạp

Ở ví dụ trên chúng ta có kết quả kiểm định Chi bình phương = 25.474 chính là kết quả từ LR test với 2 mô hình: 1) mô hình đầy đủ với 3 biến; 2) mô hình Null (không có biến x).
Df = 3 – 0 = 3
Sig = p-value < 0.05 nên bác bỏ giả thuyết H0: mô hình Null (L0) phù hợp. Tức Mô hình 3 biến (Group, Symtoms, AA) hiệu quả đưa vào phân tích hơn mô hình không có biến nào chỉ có baseline function mà thôi.
Chúng ta làm ví dụ khác
Giả sử theo các bác sĩ, việc các bệnh nhân có hoặc không tham gia vào tổ chức Alcoholics Anonymous sẽ không ảnh hưởng lên khả năng họ uống rượu trở lại, nên loại bỏ biến này ra khỏi mô hình.


Gọi mô hình Cox PH 2 biến này là L0 và 3 biến đầy đủ là L1
-2ln(likelihood ratio) = – 2*(lnL0 – lnL1) = 2lnL1 – 2lnL0 = – 163.29 – (-168.584) = 5.294
Tra bảng phân phối chi bình phương với bậc tự do df = 3 – 2 = 1
Trên bảng do 5.024 < 5.294 < 6.6 => p-value thuộc (0.01; 0.025) và sẽ < 0.05. suy ra bác bỏ H0: mô hình L0 với 2 biến phù hợp. Kết luận mô hình đầy đủ 3 biến sẽ mang lại hiệu quả phân tích nhiều hơn hay nói cách khác “fit” hơn, phù hợp.
Để biết được kết quả kiểm định có chính xác hay không chúng ta có thể tạo quy trình xây dựng mô hình theo block hay step trong phần mềm SPSS, với Block 1: chỉ có 2 biến Group và Symptoms; Block 2: cả 3 biến. SPSS sẽ cho chúng ta kết quả như sau:

Các bạn có thể thấy Chi-square ở previous step, tức là step đầu bạn bỏ vào mô hình 2 biến, step sau là 3 biến, vậy kết quả log-likelihood ratio đã thay đổi ra sao từ step sau so với step đầu. Kết quả gần bằng giá trị tính được ở trên, P-value = 0.021 < 0.05
Mô hình Interaction
Một trong những điều chúng ta quan tâm đó chính là liệu các biến độc lập X khi tác động lên tỷ lệ rủi ro h(t) có mối quan hệ với thời gian khi giả định đặt ra ban đầu là ngược lại, tức không có mối quan hệ. Chúng ta vẫn có thể xây dựng mô hình Cox PH với các biến X phụ thuộc vào thời gian (time – dependent variables) tuy nhiên nó lại không đúng với giả định, và mô hình này không còn được gọi là Cox PH mà là mô hình “mở rộng” Cox PH.
Mô hình “mở rộng” Cox PH nằm ngoại phạm vi series bài viết đầu tiên về Survival analysis. Ở chuỗi bài viết khác về phân tích sống sót trong tương lai, chúng tôi sẽ giới thiệu đến các bạn.
Như vậy để kiểm tra giả định các biến X không có liên hệ với thời gian, chúng ta phải xây dựng mô hình Cox PH dạng “interaction” – tương tác với các biến kết hợp sau đó đánh giá.
Biến kết hợp là gì? Kết hợp là tên gọi chúng tôi đặt ra để các bạn dễ hiểu hơn về loại biến này.
Ví dụ chúng ta có mô hình Cox PH như sau:
h(t) = h0(t) * exp(β1X1 + β2X2)
Trong đó 2 biến X1, X2 có mối quan hệ với nhau, mối quan hệ có thể thuận hay nghịch. Mô hình Cox PH khi thêm biến kết hợp X1, X2 được viết như sau
h(t) = h0(t) * exp(β1X1 + β2X2 + β12X1X2)
Kết hợp mà chúng tôi nói ở đây là để X1*X2 = X12 là một biến mới, còn gọi là interaction term.
Xét trong ví dụ chúng ta đang nói đến trong bài viết. Giả sử, cả 3 biến Groups, Symtoms, AA, mỗi biến đều có quan hệ với thời gian xảy ra sự kiện (thời gian đến khi bệnh nhân uống rượu trở lại, hay thời gian đến khi bệnh nhân kết thúc quá tình theo dõi mà vẫn không uống rượu trở lại)
h(t) = h0(t)*exp(-0.902Xgroup + 0.754XSymtoms – 1.04XAA + βT*groupXt-group + βT*symtompsXt-symtomps + βT*AAXt-AA)
SPSS hay các phần mềm phân tích khác cho phép xây dựng mô hình Cox PH với các biến X phụ thuộc vào thời gian, và tính năng interaction.
Chúng ta sẽ sử dụng LR test để kiểm tra với mô hình đầu tiên gồm 3 biến ban đầu và mô hình 2 thêm interaction term là Time vô mỗi biến. Tức sẽ có 6 biến tất cả
Kết quả từ SPSS
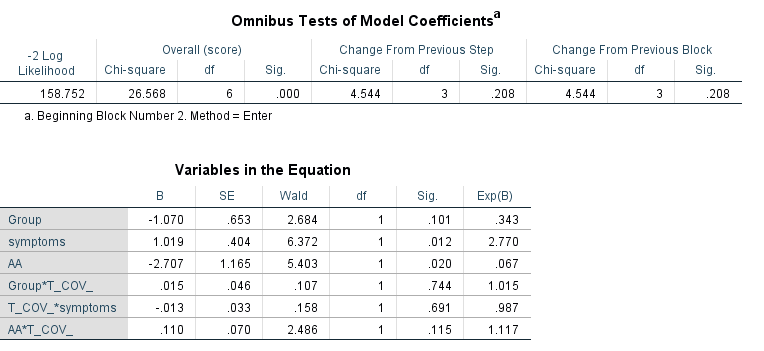
Các bạn có thể thấy p-value ở LR test = 0.208 > 0.05. Tức mô hình mới không phù hợp hơn mô hình cũ, mô hình 3 biến ban đầu vẫn hiệu quả hơn.
Ở bảng các biến trong mô hình, các biến kết hợp với thời gian đều có sig = p-value > 0.05, tức không có tác động lên biến tỷ lệ rủi ro. Nói cách khác, 3 biến Group, Symptoms và AA khả năng không có mối quan hệ với biến thời gian, và chúng ta không cần thêm vào mô hình Cox PH.
Như vậy đến đây là kết thúc bài viết phần 6, bài viết cuối cùng về lý thuyết phân tích sống sót. Kiến thức về Survival analysis mà chúng tôi trình bày xuyên suốt 6 phần chỉ là những kiến thức cơ bản để các bạn có thể giải quyết những bài toán đơn giản trong nghiên cứu tỷ lệ rời dịch vụ của khách hàng, hay các nghiên cứu khác tương tự. Và dĩ nhiên lượng kiến thức này là chưa đủ để bạn trở thành một chuyên gia trong Survival analysis nói riêng và Data mining nói chung. Còn rất nhiều phương pháp khác trong phân tích sống sót, cũng như các dạng mô hình khác trong Cox PH chúng tôi chưa thể đề cập hết đến các bạn. Hi vọng nếu có dịp, BigDataUni và các bạn sẽ tiếp tục hành trình chinh phục Survival analysis
Bật mí: chúng tôi còn 1 bài viết nữa về ứng dụng survival analysis trong lĩnh vực bán lẻ, và viễn thông với ví dụ cụ thể. Các bạn cùng chờ đón nhé.
Hẹn gặp các bạn ở chủ đề mới tuần sau!
Tài liệu tham khảo
Tài liệu nghiên cứu “Time and Change: Using Survival Analysis in Clinical Assessment and Treatment Evaluation” của 2 chuyên gia Douglas A. Luke và Sharon M. Homan
“Survival Analysis” – Lisa Sullivan
“An Introduction to Survival Analysis” – Mario Cleves và cộng sự
“Survival Analysis A Practical Approach” – David Machin và cộng sự
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English