Trải qua 3 phần bài viết về Data cleaning, làm sạch dữ liệu với task xử lý missing values chúng ta đã làm quen các khái niệm, đặc biệt là đã cùng nhau tìm hiểu các cơ chế missing values quan trọng bao gồm MCAR, MAR, MNAR, cách thức xác định trường hợp missing values có phải MCAR, và phân biệt trường hợp missing values giữa MAR và MNAR. BigDataUni cũng đã trình bày đến các bạn 2 phương pháp xử lý dữ liệu missing đầu tiên, phổ biến là Listwise và Pairwise deletion, với những lợi ích và hạn chế nhất định. Các bạn xem lại các bài viết trước của BigDataUni về Missing values theo link dưới đây nhé:
Data cleaning – làm sạch dữ liệu: Xử lý missing values (P1)
Data cleaning – làm sạch dữ liệu: Xử lý missing values (P2)
Data cleaning – làm sạch dữ liệu: Xử lý missing values (P3)
Ở phần cuối chủ đề missing values, BigDataUni sẽ giới thiệu đến các bạn những phương pháp Imputation phổ biến, đơn giản nhất – Single imputation, bao gồm khái niệm imputation, single imputation, lợi ích, khuyết điểm của mỗi phương pháp.
Các kỹ thuật Imputation phức tạp như Stochastic regression, Multivariate regression, Multiple imputation, cũng như các hướng tiếp cận mới trong xử lý missing values như Maximum likelihood Estimation và Bayesian Estimation chúng tôi sẽ gửi đến các bạn ở bài viết sau.

Vậy Imputation là gì?
Imputation hướng tiếp cận chính, được hầu hết mọi chuyên gia trong ngành Data science ưu tiên sử dụng khi phải đối mặt với các vấn đề missing values.
Nhìn ở góc độ tổng thể nếu chưa biết đến các phương pháp xử lý missing values, nhìn vào các ô trống trong một bảng dữ liệu, những ô không chứa giá trị, tức giá trị của chúng bị thiếu thì bạn có thể làm gì? Thứ nhất không quan tâm đến chúng, mặc kệ chúng, loại bỏ chúng chỉ sử dụng các giá trị còn lại trong tập dữ liệu để thực hiện những phân tích mà mình cần (đây còn gọi là Listwise hoặc Pairwise deletion). Thứ hai “liều một phen”, bằng nhiều cách “dự báo”, “phỏng đoán”, hay “đo lường” để thêm những giá trị vào chính các ô trống ấy với một độ tin cậy nhất định rằng chúng sẽ gần giống chính các giá trị bị missing trong thực tế, sẽ hạn chế được ảnh hưởng của missing values lên kết quả phân tích, và có thể cung cấp nhiều thông tin hữu ích cho các chuyên gia phân tích. Cách thứ hai chính là giải thích đơn giản của phương pháp Imputation.
Imputation đơn giản là thay thế những giá trị bị missing, thêm vào các giá trị, là các kết quả có được thông qua thực hiện các phương pháp tính toán, định lượng phù hợp, sau đó tiến hành phân tích tập dữ liệu đã đầy đủ, coi như các giá trị được “imputed”chính là các giá trị bị missing.
Xét theo từng đối tượng, từng quan sát trong tập dữ liệu thì mỗi giá trị impute mô tả chính đối tượng và chính quan sát không nên “tin tưởng” tuyệt đối vì chúng mới chỉ được “ước lượng”. Ví dụ để thống kê điểm thi học kỳ của khối lớp 10 báo cáo nhanh cho ban giám hiệu, các thầy cô giáo đã tổng hợp dữ liệu thì thấy có 20 em trong số 1000 học sinh không có điểm môn toán do quá trình chấm điểm chưa xong vì nhiều nguyên nhân khác nhau, giả sử dựa vào dữ liệu điểm trong quá trình học, các thầy cô ước lượng nhanh điểm toán của 20 em này, để tiến hành thống kê. Tuy nhiên, các điểm số này sẽ được ký hiệu đặc biệt để lưu ý là không được công bố đến 20 học sinh này, vì chúng không chính xác, cũng như không được kết luận gì về học lực môn Toán của các bạn này.
Imputation phụ thuộc hoàn toàn vào những giá trị không bị missing trong tập dữ liệu, và nếu chúng có vấn đề (chẳng hạn bị outliers, nhiều giá trị không hợp lý) thì chắc chắn sẽ không hiệu quả.
Mục đích của các chuyên gia khi thực hiện Imputation chính là cố gắng giữ được những giá trị missing càng nhiều càng tốt (để đưa vào phân tích) bằng cách tìm ra một tập những giá trị thay thế sao cho “hợp lý” nhất theo cảm nhận, kinh nghiệm và các phương pháp đo lường. Các bạn tham khảo những tài liệu tiếng anh về Data cleaning sẽ thường bắt gặp từ “plausible” – dịch ra “có vẻ hợp lý” – đây là “kim chỉ nam” phải hướng đến để xây dựng một tập dữ liệu mẫu, với missing values được thay thế mà phải “plausible”, như được lấy từ tổng thể nghiên cứu.
Hơn nữa, những dữ liệu Imputed và dữ liệu Observed (dữ liệu không bị missing ban đầu) khi tổng hợp, ở bất kỳ giả định nào, cũng cần phải thể hiện các đặc tính vốn có của dữ liệu mẫu thực tế. Cụ thể, tập dữ liệu mẫu mới với missing values đã được xử lý, sẽ có các tham số mẫu được ước lượng không khác biệt quá nhiều so với những tham số mẫu thực tế.
Imputation khắc phục khuyết điểm chính từ 2 phương pháp mà bài viết trước chúng ta đã đề cập là Listwise và Pairwise deletion: đảm bảo dữ liệu không bị mất hoàn toàn, mẫu dữ liệu vẫn đủ, vẫn có cách “khôi phục” các giá trị missing sao cho gần giống thực tế, từ đó cải thiện độ chính xác của kết quả phân tích dữ liệu sau cùng, hạn chế tối đa những ảnh hưởng mà missing values đem lại. Imputation giúp cải thiện chất lượng của tập dữ liệu giúp các chuyên gia khai phá những thông tin hữu ích bên cạnh giảm bớt những lo ngại do missing values.
Như vậy chúng ta đã tìm hiểu sơ lược khái niệm Imputation, và tầm quan trọng của nó. Điều chúng ta cần quan tâm tiếp theo, chính là yếu tố “plausible” của dữ liệu imputed. Để đảm bảo được yếu tố này thì hàng loạt các phương pháp Imputation được ra đời, và được cải tiến liên tục, bắt đầu từ những kỹ thuật đơn giản nhất như Single imputation cho đến Multiple imputation với quy trình thực hiện phức tạp hơn.
Imputation được chia làm 2 loại chính là Single imputation và Multiple imputation, bao gồm các phương pháp áp dụng cho trường hợp missing values dữ liệu là dữ liệu định tính (categorical/ qualitative) và trường hợp missing values dữ liệu là dữ liệu định lượng (continuous/ quantitative). Imputation áp dụng chính cho trường hợp missing values là MAR, nhưng vẫn có thể áp dụng cho MCAR (thưởng chỉ tính Mean imputation) và MNAR (riêng trường họp MNAR thường rất phức tạp, và phương pháp sử dụng là Multiple imputation)
Trong bài viết này, chúng tôi sẽ chỉ giới thiệu một số phương pháp thông dụng, còn các cách thức impute khác mà chúng tôi không nhắc đến, các bạn có thể tham khảo những tài liệu khác. Bài viết có giới hạn nên chúng tôi không thể trình bày chi tiết tất cả các phương pháp mong các bạn thông cảm!
Single imputation
Single imputation là phương pháp xác định, ước lượng, dự báo một giá trị cụ thể để thay thế cho một vị trí dữ liệu (data point) bị missing giá trị, hiểu đơn giản ví dụ chúng ta xem tại mỗi ô trong bảng dữ liệu, nếu ô đó bị mất giá trị, chúng ta sẽ tiến hành thêm giá trị vào, và giá trị này có được dựa trên phân tích, tính toán các giá trị còn lại trong tập dữ liệu đó.
Cách giải thích khác quan trọng hơn cần nắm, mỗi giá trị thay thế được tính trên 1 tập dữ liệu chung (không chia nhỏ), và mỗi missing value sẽ được thay thế 1 lần với chỉ một giá trị mà thôi. Khác với Multiple imputation mà chúng tôi sẽ đề cập ở bài viết khác sắp tới.
Single imputation giúp chúng ta có một tập dữ liệu đầy đủ để phân tích tuy nhiên để khẳng định dữ liệu có chất lượng cao nhất thì hoàn toàn không thể. Nguyên nhân, Single imputation vẫn khiến các tham số tính toán từ dữ liệu bị “biased” ví dụ như các số trung bình, các hệ số tương quan, hệ số hồi quy, nhưng cũng tùy vào mỗi phương pháp áp dụng, cơ chế missing values, tỷ lệ dữ liệu bị missing, và tất cả các giá trị còn lại không bị missing trong tập dữ liệu. Thực chất các giá trị được thêm vào xuất phát từ việc ước lượng và dự báo, nên không nói chúng ta cũng biết được chúng không chính xác hoàn toàn, hay nói cách khác chúng không giống một cách tuyệt đối các giá trị thực tế đã bị missing. Làm thế nào để triển khai một kỹ thuật Single imputation nhưng hạn chế tối đa vấn đề bị sai lệch thực sự không dễ dàng.
Missing values có thể làm tăng sai số chuẩn của mẫu do chúng ảnh hưởng đến độ chính xác trong việc ước lượng các tham số. Tuy nhiên khi chúng ta áp dụng single imputation, coi các giá trị được thay thế là giá trị thực, và không tính đến các phương pháp thống kê suy luận, thì có thể làm giảm sai số chuẩn, không những vậy có thể làm giảm p-value (tăng khả năng bác bỏ H0 nhưng H0 lại đúng – sai lầm loại I) sẽ ảnh hưởng các kết quả kiểm định áp dụng cho tập dữ liệu, và cả việc ước lượng khoảng tin cậy (các khoảng ước lượng bất kỳ có thể nhỏ đi, thiếu tính chính xác). (theo Roderick J.A.Little, Donal B.Rubin, “Statistical Analysis with missing data”)
Chúng ta cùng nhìn thử qua ví dụ dưới đây để thấy được vấn đề giảm sai số chuẩn ghi áp dụng Single imputation:
Ví dụ một mẫu dữ liệu gồm 100 quan sát với 1 biến bất kỳ, trong có có 60 quan sát là có dữ liệu, 40 quan sát còn lại không có. Chúng ta tính được trung bình mẫu, và độ lệch chuẩn của mẫu theo những giá trị có từ 60 quan sát, lần lượt là 50 và 10. Giả sử missing values là một trong 2 trường hợp MCAR, MAR. Trung bình mẫu được dùng kết luận hay ước lượng cho trung bình tổng thể, ở đây chúng tạm sử dụng ước lượng điểm cho đơn giản, vậy trung bình tổng thể cũng sẽ dao động gần con số 50, sai số chuẩn theo công thức sẽ bằng s/căn N với s là độ lệch chuẩn, N là số quan sát dùng để tính trung bình, như vậy sẽ là 60. Sai số chuẩn của mẫu so với tổng thể (chênh lệch giữa giá trị trung bình của mẫu, và trung bình của tổng thể) = 10/căn bậc 2(60)
Mỗi quan sát trong 40 quan sát bị missing sẽ được impute giá trị thay thế bằng cách lấy ngẫu nhiên một giá trị trong số 60 quan sát còn lại. Khi chúng ta đưa tập dữ liệu này vào phần mềm phân tích hay phần mềm thống kê nào đó thì chúng sẽ phân tích như 100 quan sát này đều có giá trị thực, không phân biệt được đâu là missing value đã được imputed đâu là giá trị observed. Lúc này trung bình mẫu tính trên 100 quan sát có thể gần bằng 50 và độ lệch chuẩn gần bằng 10 nhưng sai số chuẩn đã giảm 10/căn 2 (100) < 10/căn 2 (60).
Kết quả không hợp lý vì 40 quan sát bị missing hoàn toàn không cho chúng ta bất kỳ thông tin gì khác ngoài các giá trị chúng ta lấy từ 60 quan sát để impute.
Theo thống kê, sai số chuẩn giảm khi số quan sát trong dữ liệu mẫu lớn và gần bằng số quan sát của tổng thể nghiên cứu. Nhưng ở đây sai số chuẩn bị giảm không phải do chúng ta lấy mẫu nhiều hơn khi khảo sát mà là số quan sát với những giá trị “ảo” được chúng ta “tự” thêm vào.
Hơn nữa, đáng lẽ sai số chuẩn của tập dữ liệu sau khi thực hiện impute phải cao hơn 10/ do chúng ta đã “make-up” dữ liệu, trung bình của mẫu có thể sẽ khác biệt nhiều so với trung bình tổng thể, khi chúng ta đang cố làm “nhiễu loạn” tập dữ liệu. Nhưng đằng này sai số chuẩn lại nhỏ dần. Đây là một lưu ý quan trọng và cần cân nhắc khi thực hiện single imputation.
Single imputation là phương pháp “vừa quyến rũ” và “vừa nguy hiểm”. Quyến rũ là do nó đưa các nhà phân tích vào trạng thái an tâm khi dữ liệu đã đầy đủ, họ có thể sẵn sàng phân tích. Nhưng nguy hiểm ở đây đó là đưa các nhà phân tích vào chính cái bẫy rằng họ nghĩ dữ liệu đang phản ánh và cung cấp thông tin trong thực tế, khiến họ tin vào các kết quả phân tích nhưng sự thật chúng không chính xác
Tuy nhiên, mặc dù Single imputation có nhiều hạn chế như đã nói. Nhưng chúng vẫn mang lại những lợi ích nhất định. Thứ nhất, single imputation là cơ sở để triển khai multiple imputation, nói là cơ sở do một số phương pháp trong single imputation sẽ hỗ trợ bước đầu tiên của multiple imputation ví dụ regression imputation (chi tiết của phương pháp này chúng tôi sẽ trình bày ở phần cuối bài viết).
Thứ hai, single imputation hỗ trợ xử lý missing values trường hợp dữ liệu missing value có tỷ lệ thấp, chỉ vài quan sát bị missing (các giá trị thêm vào sẽ không tác động nhiều đến các tham số thống kê), và mẫu dữ liệu không lớn không cho phép chúng ta loại bỏ các quan sát này như Listwise deletion hay áp dụng Pairwise deletion lại không hiệu quả. Hơn nữa, muốn đơn giản quá trình phân tích (trường hợp chưa biết dùng đến các phần mềm phân tích chuyên dụng), thì Single imputation là phương pháp có thể phù hợp.
Trường hợp tỷ lệ missing data quá nhiều bất kể kích thức mẫu, biến nào cũng có missing values, mẫu dữ liệu lại lớn, phức tạp và chúng ta quan tâm nhiều đến tầm ảnh hưởng của missing values lên kết quả phân tích, thì không nên dùng single imputation mà thay vào đó là Multiple imputation. Chúng ta cùng đi vào tìm hiểu một số phương pháp trong single imputation
CONSTANT IMPUTATION
Mean imputation
Mean imputation hay còn gọi Mean substitution là phương pháp thay thế các giá trị missing values bằng một số trung bình (mean) tính trên những giá trị còn lại trong tập dữ liệu mà không bị missing. Đây là một trong các kỹ thuật imputation ra đời đầu tiên. Mặc dù thỏa mãn yêu cầu của nhà phân tích là xây dựng được một tập dữ liệu đầy đủ không có missing values, nhưng lại là phương pháp cho thấy nhiều khuyết điểm nhất của Imputation nói chung và Single Imputation nói riêng.
Lấy lại ví dụ của bài viết trước, ví dụ tham khảo từ tài liệu “Applied Missing Data Analysis” của tác giả Craig K.Enders.
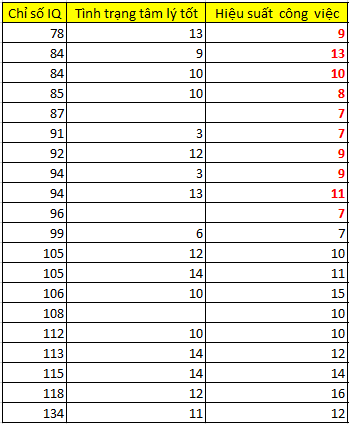
Dưới đây là bảng dữ liệu nhỏ có missing values dạng MAR đã được xác định trước đó. Dữ liệu cung cấp thông tin về những ứng viên được khảo sát cho mục đích chọn lựa trở thành nhân viên chính thức, các ứng viên sẽ thực hiện bài kiểm tra về IQ, bài đánh giá về thể trạng tâm lý trong buổi phỏng vấn (điểm cao ứng với tình trạng tâm lý tốt), hiệu suất công việc được các giám sát viên theo dõi và đánh giá trong 6 tháng.
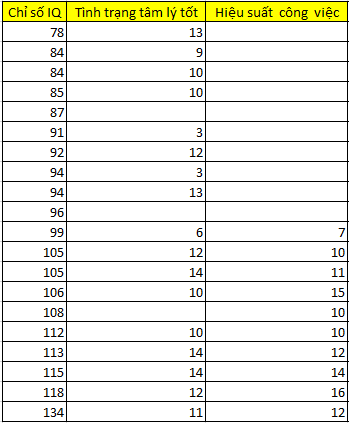
Chúng ta sẽ thay thế các giá trị missing tại biến hiệu suất công việc bằng số trung bình của 10 giá trị còn lại trong biến. Trung bình = (117)/10 = 11.7. Chúng ta làm tương tự cho biến tình trạng tâm lý tốt với số trung bình thêm vào = (176)/17 = 10.35. Kết quả như sau:
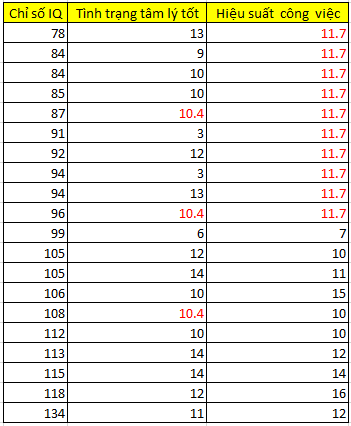
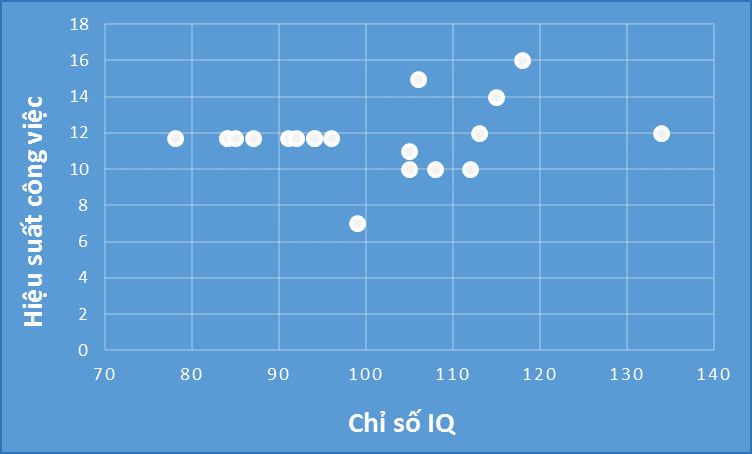
Các bạn có thể thấy các chấm tròn trên cùng 1 hàng chính là các giá trị chúng ta vừa thêm vào, lúc này mối quan hệ tương quan giữa chỉ số IQ, và hiệu suất công việc được thể hiện trên đồ thị là không có, hệ số tương quan sẽ bằng 0 nếu chỉ tính riêng các giá trị mới impute, còn nếu xét tất cả quan sát thì khả năng hệ số tương quan sẽ nhỏ.
Hệ số tương quan cho tập dữ liệu đầy đủ không bị missing đề cập ở bài viết trước

Còn trường hợp lần này:

Các bạn có thể thấy hệ số tương quan đầu tiên là 0.54 giảm còn 0.20.
Tuy nhiên đối với biến tình trạng tâm lý tốt, hệ số tương quan với chỉ số IQ chỉ tăng nhẹ từ 0.23 lên 0.27, không bị tác động nhiều bởi các giá trị mới thêm vào. Chúng ta cùng nhìn qua đồ thị dưới đây.
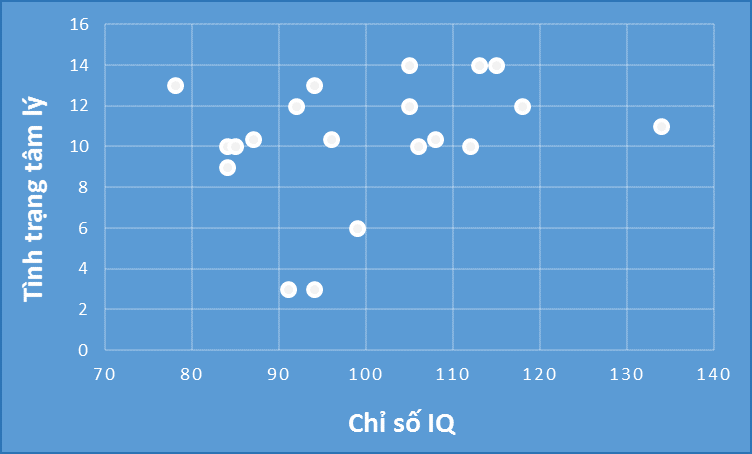
Các điểm dữ liệu không tập trung trên 1 hàng, không nghiêng về một phía, tức vấn đề “biased” bị hạn chế.
Tiếp theo chúng ta thử tính phương sai, độ lệch chuẩn so sánh 2 biến mới được imputed với dữ liệu đầy đủ.
Độ lệch chuẩn của 2 biến khi trường hợp dữ liệu đầy đủ, lấy lại số liệu ở bài viết trước (phần 3)
Stình trạng tâm lý = 3.2
SHiệu suất công việc = 2.7
Độ lệch chuẩn của 2 biến khi dữ liệu missing đã được imputedbởi giá trị trung bình
Stình trạng tâm lý = 3.17
SHiệu suất công việc = 1.8
Công thức tính độ lệch chuẩn
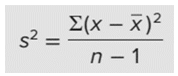
Biến hiệu suất công việc sau khi được imputed có độ lệch chuẩn giảm mạnh, ngược lại với biến tình trạng tâm lý.
Qua đây có thể thấy được khuyết điểm của mean imputation xảy ra rõ nhất khi tỷ lệ dữ liệu missing lớn, tức mean imputation không phù hợp áp dụng khi missing values là quá nhiều. Tỷ lệ missing values ở biến tình trạng tâm lý chỉ là 3/20 = 15%, còn biến hiệu suất công việc lên tới 50% (10/20). Mean imputation “có thể” là công cụ hữu hiệu khi tập dữ liệu có rất ít missing values và là trường hợp ngẫu nhiên.
Tuy nhiên, theo các chuyên gia, nếu các nghiên cứu, khảo sát chỉ dừng lại ở mục đích thống kê thông tin, cung cấp các hiểu biết tổng quan về đối tượng nghiên cứu (chủ yếu ở lĩnh vực khoa học xã hội) thì mean imputation có thể được sử dụng vì tính đơn giản và nhanh chóng. Nhưng nếu mục đích phân tích dữ liệu là để ra quyết định chẳng hạn như trong ngành y, hay thậm chí ở ví dụ này là lựa chọn nhân viên, thì bất kể trường hợp nào, dẫu missing values có ít thì hoàn toàn không nên sử dụng mean imputation.
Mean imputation áp dụng cho biến với dữ liệu có missing values là dữ liệu định lượng, còn dữ liệu định tính thì chúng ta sẽ sử dụng Mode – giá trị định tính có tần suất xuất hiện nhiều nhất trong một biến.
Ví dụ 80% nhân viên đến từ miền Nam, 10% nhân viên đến từ miền Bắc, 5% miền Trung còn lại là missing values. Thì 5% missing values sẽ được thêm vào “đến từ miền Nam”. Vậy sẽ có 85% nhân viên đến từ miền Nam.
Tương tự như Mean imputation, Mode imputation tuy đơn giản nhưng lại có nhiều vấn đề như sẽ ảnh hưởng đến hệ số tương quan giữa các biến nếu missing values là quá nhiều. Mode imputation và Mean imputation là 2 phương pháp được các chuyên gia coi là “tệ nhất” trong xử lý missing values ở giai đoạn hiện nay khi ngành Data science đang phát triển mạnh mẽ. Các phần mềm phân tích tiên tiến và hàng loạt kỹ thuật phân tích tinh vi được ứng dụng nhiều hơn.
Mode và mean imputation là dạng imputation không có điều kiện ràng buộc, hiểu đơn giản, là các giá trị được imputed lấy ra từ chính biến bị missing values, không xét đến các biến còn lại trong tập dữ liệu, hay bị kiểm soát bởi bất kỳ điều kiện nào đề ra trước đó.
Ngoài Mean và mode imputation, còn có Median imputation – thay thế missing values bằng giá trị trung vị của biến, và Zero imputation – thay thế giá trị missing values bằng giá trị số 0.
Khi phân phối xác suất của tập dữ liệu không theo quy luật phân phối chuẩn (Nornaml distribution) thì Median imputation phù hợp để thay thế các missing values, do giá trị median đo lường khuynh hướng tập trung (central of tendency) tốt hơn giá trị trung bình mean, nhưng cũng không cải thiện được các vấn đề mà mean imputation đem lại đặc biệt là định lượng mối quan hệ các biến kém chính xác. Còn Zero imputation phù hợp sử dụng khi các missing values có thể mang giá trị “0” mà không đánh mất tính hợp lý, hay missing values không có ý nghĩa để phân tích. Ví dụ id của khách hàng khi missing có thể thay thế bằng 0, bằng bỏ qua vì chúng ta không phân tích đến chúng, hay trong bài kiểm tra học lực, các học sinh không trả lời các câu hỏi đầy đủ, khi chấm điểm, dựa trên nguyên tắc phải trả lời đủ các câu thì mới tính điểm, thì lúc này missing values sẽ được thay bằng 0.
Các bạn có thể tham khảo thêm các tài liệu khác để biết thêm các trường hợp ứng dụng Median imputation và Zero imputation. Ngoài ra, cả 4 dạng imputation này còn được gọi là Constant imputation, tức các giá trị missing được thay thế bởi 1 hằng số duy nhất, không thay đổi, do đó chúng vẫn mang nhiều khuyết điểm, và được các chuyên gia khuyến cáo không nên sử dụng hoặc nếu phải sử dụng thì cần cân nhắc thật kỹ.
RANDOM IMPUTATION
Random imputation là phương pháp thay thế các missing values bằng các giá trị được lấy ngẫu nhiên trong tập dữ liệu (các giá trị observed) hiện tại – gọi là hot-deck imputation hoặc các giá trị được lấy ngẫu nhiên ở tập dữ liệu khác nhưng có cùng các biến – gọi là cold-deck imputation.
Có 2 hướng tiếp cận trong việc ứng dụng phương pháp Random imputation. Trong đó thứ nhất, là sử dụng các giá trị sẵn có trong tập dữ liệu để tiến hành quy trình thay thế trên cơ sở chọn lựa ngẫu nhiên nhưng đảm bảo tính phù hợp – hướng tiếp cận theo kinh nghiệm. Thứ hai là các giá trị imputed ngẫu nhiên phải đảm bảo tuân theo một giả định về quy luật phân phối nào đó ví dụ phân phối chuẩn – hướng tiếp cận theo lý thuyết phức tạp hơn. Trong phạm vi bài viết lần này chúng ta chỉ tập trung vào hướng tiếp cận thứ nhất. Các bạn có thể tham khảo thêm ở các tài liệu khác hướng tiếp cận thứ hai.
Mặc dù cả 2 quy trình Hot và cold-deck hướng đến giá trị được imputed phải xuất phát từ một quy trình lựa chọn ngẫu nhiên nhưng một số cách thức lại có phần bị ràng buộc ở một số điều kiện khác nhau, chúng tôi sẽ trình bày chi tiết dưới đây
Hot-deck imputation
Có nhiều cách giải thích khác nhau về Hot-deck imputation, hay nói cách khác có nhiều phương pháp trong Hot-deck imputation. Từ hot-deck hiểu theo nghĩa bóng là “thẻ bài nóng”, quan sát có giá trị bị missing thì giá trị bị missing sẽ được thay thế ngay bằng chính giá trị của các quan sát còn lại tập dữ liệu (ngay cả khi dữ liệu đang được thu thập). Mỗi quan sát còn lại giống như một thẻ bài có ghi giá trị, và sẽ được bốc ngẫu nhiên để impute. Giải thích như vậy mong các bạn sẽ hiểu về thuật ngữ này.
- Thay thế dữ liệu còn thiếu với những giá trị của các quan sát khác một cách ngẫu nhiên. Đây là phương pháp đơn giản và dễ hiểu nhất. Ví dụ một khách hàng không cung cấp thông tin về giới tính trong cuộc khảo sát xu hướng tiêu dùng thực phẩm sạch, nghiên cứu tập trung nhóm đối tượng người tiêu dùng nữ nên tỷ lệ 70% quan sát là nữ, 25% là nam, 3% không xác định, còn lại bị missing, thì khả năng cao missing values sẽ được thay ngẫu nhiên là “giới tính nữ”.
- Thay thế dữ liệu còn thiếu với những giá trị của các quan sát khác từ một mẫu nhỏ được lấy ra từ tập dữ liệu mẫu (subsample) nhưng với điều kiện các quan sát này có sự tương đồng với những quan sát bị missing values. Ví dụ một cuộc khảo sát khách hàng từ chối cung cấp thông tin về thu nhập hàng tháng. Chuyên gia phân tích sẽ phân tập dữ liệu thành các nhóm khách hàng có đặc điểm nhân khẩu học (tuổi, giới tính, tình trạng hôn nhân, nơi sinh sống,…) khác nhau, và các nhóm này khách hàng đều cung cấp thông tin về thu nhập. Các khách hàng nào có missing values, sẽ được kiểm tra về đặc tính nhân khẩu học, nếu thuộc nhóm này, thì missing value sẽ được thay thế bởi cách chọn ngẫu nhiên các giá trị trong nhóm ấy, ở đây là các giá trị về thu nhập hàng tháng. Lưu ý các biến dữ liệu có thể là biến định lượng, vì các thuật toán tinh vi trong hot-deck imputation có thể xây dựng các nhóm tương đồng một cách hiệu quả không khác gì biến định tính. (theo Craig K.Enders, “Applied missing data analysis”) Dạng này còn có tên gọi khác là “Similar response pattern imputation”.
- Cách thứ 3 là thay thế giá trị missing một cách ngẫu nhiên từ các giá trị của những quan sát có data point – điểm dữ liệu gần nhau, gần giống phương pháp K-NN (K láng giềng gần nhất).
Hot-deck imputation được sử dụng trong lĩnh vực nghiên cứu khảo sát. Hot-deck imputation có thể không ảnh hưởng đến quy luật phân phối (distribution) của dữ liệu và tác động của nó lên sai số chuẩn, độ lệch chuẩn không mạnh bằng các phương pháp vừa nói ở trên. Do các giá trị được imputed là ngẫu nhiên, và có thể khác nhau, không phải tất cả giống nhau cùng chung 1 giá trị. Tuy nhiên vẫn phải nhớ tránh cái “bẫy” mà chúng tôi đã đề cập khi nói đến single imputation.
Cold – deck imputation
Phương pháp này khác với Hot-deck là các giá trị được imputed sẽ lấy từ các tập dữ liệu khác, không phải từ tập dữ liệu hiện tại, nhưng vẫn đảm bảo sự giống nhau trong các thuộc tính dữ liệu. Cold – deck cũng giống Hot – deck là được ứng dụng chính trong lĩnh vực nghiên cứu khảo sát.
Ví dụ một chuyên gia phân tích tách tập dữ liệu thành 2 phần, một phần được dùng để phân tích các đối tượng nghiên cứu và đưa ra các giả định, các kết luận, phần còn lại được dùng để kiểm tra liệu các giả định và kết luận có hợp lý (nôm na thì gần giống training và test data). Dữ liệu bị missing ở mỗi phần dữ liệu sẽ được thay thế ngẫu nhiên bởi các giá trị có trong phần dữ liệu còn lại.
Cold – deck imputation cũng mang trong nhiều vấn đề tương tự như Hot-deck nói riêng và Single imputation nói chung và vì thế cũng được các chuyên gia khuyến cáo sử dụng nếu mục đích phân tích dữ liệu không chỉ dừng ở thống kê, cung cấp thông tin hữu ích mà là để ra các quyết định quan trọng, nghiên cứu chuyên sâu về đối tượng nghiên cứu.
Tuy nhiên Hot-deck và cold-deck vẫn được đánh giá cao hơn Constant imputation mà cụ thể là mean, mode, median, và zero imputation vì nó hạn chế được vấn đề “biased” của dữ liệu, đảm bảo tính “tự nhiên” của tập dữ liệu.
Thế nhưng các dữ liệu được imputed ở cả Constant và Random imputation lại không có các điều kiện để dựa vào đó đánh giá tính “plausible” hoặc nếu có cũng không chặt chẽ ví dụ hot-deck dựa vào nét tương đồng giữa các quan sát để tiến hành phân nhóm, và lấy ngẫu nhiên giá trị ở mỗi nhóm để impute cho các quan sát có missing values thuộc nhóm đó, chứ không có phương pháp định lượng cụ thể rằng mỗi giá trị được imputed nếu đúng với thực tế hay không đúng với thực tế sẽ có sai số ra sao, và mối quan hệ giữa nó với các biến còn lại trong tập dữ liệu được định lượng như thế nào? Chúng ta cùng đến với dạng imputation có điều kiện.
CONDITIONAL IMPUTATION
Có 2 dạng điều kiện: dạng điều kiện chỉ xét trên một biến khác còn lại so với biến có missing values trong tập dữ liệu, và dạng điều kiện xét trên nhiều hơn một biến khác còn lại trong tập dữ liệu.
Dạng thứ nhất bao gồm Conditional mean imputation, Last observation carried forward, Next observation carried forward, chúng tôi sẽ giới thiệu sơ lược, các bạn có thể tham khảo thêm ở những tài liệu khác.
Conditional mean imputation
Thay thế các giá trị missing bằng giá trị trung bình nhưng có xét đến điều kiện trên một biến phân loại khác. Ví dụ một vài quan sát trong nhóm khách hàng nam bị missing values ở biến thu nhập hàng tháng, như vậy khi áp dụng phương pháp mean imputation chúng ta không tính giá trị trung bình lấy trên tất cả các quan sát còn lại trong biến đó (sẽ bao gồm các giá trị thu nhập của các khách hàng nữ) mà chỉ tính trung bình các giá trị thu nhập của khách hàng nam mà thôi để tiến hành impute. Phần nào phản ánh lý do thu nhập của người giới tính nam có thể sẽ khác người giới tính nữ nên không thể gộp tất cả các giá trị còn lại tại biến thu nhập để tính trung bình. Biến missing sẽ là biến thu nhập, và biến điều kiện hay biến phân loại sẽ là biến giới tính.
Last Observation carried forward (LOCF)
Phương pháp này áp dụng cho các công trình nghiên cứu, khảo sát, hay khai phá dữ liệu mà nguồn dữ liệu thu thập theo nhiều gian đoạn khác nhau trong một khoảng thời gian dài, với cùng các đối tượng nghiên cứu, với cùng các quan sát. Phương pháp này còn được gọi là “last value carried forward”. Ví dụ thu thập dữ liệu tiền gửi hàng tháng của các khách hàng thân thiết tại 1 ngân hàng trong 6 tháng, nếu tháng thứ 6 dữ liệu bị missing thì có thể lấy dữ liệu tháng thứ 5 để impute trên cơ sở giả định rằng dữ liệu của tháng gần nhất là dữ liệu “dự báo” tốt nhất cho tháng tiếp theo. Đây cũng là giả định chung cho mọi trường hợp áp dụng LOCF. Phương pháp này thích hợp áp dụng cho dữ liệu time series hay còn gọi dữ liệu chuỗi thời gian. Time series là một thuật toán phân tích dự báo rất hay, BigDataUni sẽ giới thiệu đến các bạn trong các bài viết sắp tới.
Next value carried backward (NVCB)
Khác với LOCF, NVCB impute giá trị cho các trường hợp missing xảy ra ở khoảng thời gian trong quá khứ với dữ liệu ở thời điểm hiện tại. Ví dụ ở trên giả sử dữ liệu khách hàng bị missing ở tháng thứ 5 thì giá trị được impute sẽ lấy từ tháng thứ 6.
LOCF và NVCB là 2 phương pháp có tên gọi khác là within – subject imputation tức sử dụng chính giá trị trước và sau thời điểm bị missing values của quan sát đó để thực hiện impute.
Dạng thứ 2, thì dạng này hiểu đơn giản là chúng ta sẽ sử dụng dữ liệu ở những biến còn lại để làm cơ sở dự báo, ước lượng cho giá trị mới để tiến hành impute.
Tại sao lại có dạng thứ 2, là do nếu dạng thứ nhất, một quan sát bị missing value ở một biến bất kỳ, cũng bị missing value ở biến điều kiện luôn thì làm sao có thể xác định giá trị để impute nếu biến điều kiện chỉ có 1.
Hơn nữa ưu điểm của dạng thứ 2 là xem xét tất cả các giá trị bên trong tập dữ liệu, xem xét mối quan hệ giữa biến có missing values với những biến còn lại. Các giá trị mới sẽ có độ tin cậy cao hơn và có khả năng đáp ứng được tính “plausible” – tính hợp lý.
Trong lĩnh vực Data mining để xây dựng một mô hình thể hiện mối quan hệ giữa các biến tốt nhất thì chắc không còn phương pháp nào khác ngoài phân tích hồi quy – Regression analysis.
Nếu dữ liệu bị missing là biến định lượng thì chúng ta có thể xây dựng mô hình linear regression với biến mục tiêu y là biến bị missing cần được dự báo giá trị để impute và một biến độc lập x nào đó. Nhưng do trong thực tế tập dữ liệu thường nhiều hơn 2 biến nên có thể có nhiều hơn 1 biến độc lập x, vì vậy mô hình chúng ta xây dựng sẽ là Multiple linear regression. Nếu dữ liệu bị missing là dữ liệu định tính, không phải số thì chúng ta có thể áp dụng logistic regression
Các bạn có thể xem lại các bài viết của chúng tôi về Linear regression, Multiple linear regression, Logistic regression ở mục Blog.
Các thuật toán dự báo và phân loại dữ liệu khác trong Data mining tương tự có thể áp dụng để tính toán các giá trị mới được đưa vào impute cho các quan sát có missing values, ví dụ như KNN (K – nearest neighbor – K láng giềng gần nhất) hay CART (thuật toán cây quyết định),…
Vì bài viết có giới hạn, và nội dung lần này trọng tâm hướng đến các phương pháp đơn giản nhất trong imputation nên trước mắt chúng tôi sẽ ví dụ cho các bạn trường hợp sử dụng linear regression để dự báo giá trị bị missing. Multiple linear và logistic hay multi logistic regression chúng tôi, như đã nói ở phần giới thiệu, sẽ gửi đến các bạn ở bài viết sau
Lấy lại ví dụ ban đầu:
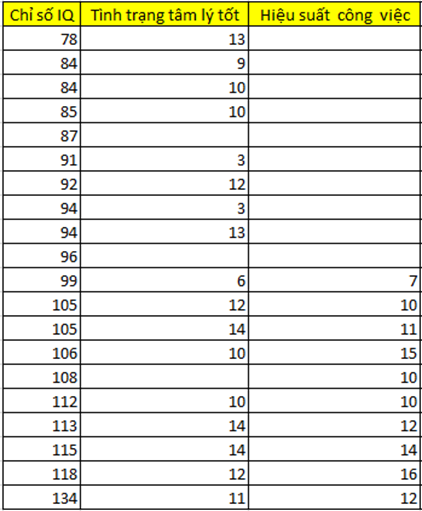
Trước khi đi vào thực hiện, chúng ta cần lưu ý các biến dự báo, hay biến độc lập x phải đủ giá trị ở tất cả các quan sát thì mới đưa vào phương trình hồi quy. Lưu ý khi thực hiện tính toán phương trình hồi quy, tập dữ liệu đầu vào phải là những quan sát có đầy đủ giá trị ở tất cả các biến.
Ví dụ Yhscv = β0 + β1*XIQ + β2*Xtttl (hscv: hiệu suất công việc, tttl: tình trạng tâm lý) tuy nhiên do biến tình trạng tâm lý là biến có 1 missing value ở 10 quan sát từ quan sát có chỉ số IQ là 99 cho đến 134. Nên phương trình hồi quy chỉ còn như sau:
Yhscv = β0 + β1*XIQ
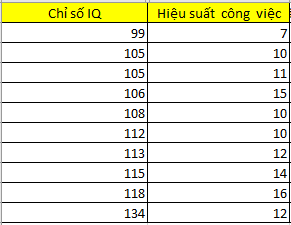
Phương trình hồi quy đơn giản tìm được:

Yhscv = -2.065 + 0.123*XIQ
Lưu ý các bạn nào chưa biết đến linear regression thi xem qua bài viết của chúng tôi dưới đây:
Correlation (tương quan) & Simple linear regression (hồi quy tuyến tính đơn giản)
Phương pháp kiểm định trong tương quan và hồi quy tuyến tính đơn biến
Nếu không biết trước về linear regression thì những gì chúng tôi đề cập dưới đây các bạn sẽ không hiểu.

Thông thường nếu có được phương trình trên chúng ta sẽ có thể dự báo được các giá trị missing bằng cách thay các chỉ số IQ của các quan sát có missing values tại biến hiệu suất công việc thì sẽ tính được giá trị hiệu suất công việc có thể impute. Tuy nhiên nếu bỏ qua các phương pháp đánh giá độ phù hợp của mô hình hồi quy trong việc dự báo mà tiến hành tìm giá trị impute thì chắc chắn các giá trị mới này sẽ không chính xác.
Trên bảng Anova các bạn có thể thấy kiểm định F, tại cột p-value = 0.2 (significance F) không nhỏ hơn mức ý nghĩa mặc định là 0.05. Nên không bác bỏ H0 tức biến hiệu suất công việc không có mối liên hệ tuyến tính với biến IQ. Theo lý thuyết của regression analysis, thì phương trình này không thích hợp để dự báo. Hệ số hồi quy = 0.123 phần nào cũng phản ánh được điều này, khi biến IQ thay đổi 1 đơn vị thì biến hiệu suất công việc chỉ thay đổi 0.123 đơn vị, rất nhỏ.
Tiếp theo giả sử chúng ta thay thế các giá trị IQ vào để dự báo giá trị missing tại biến hiệu suất công việc:
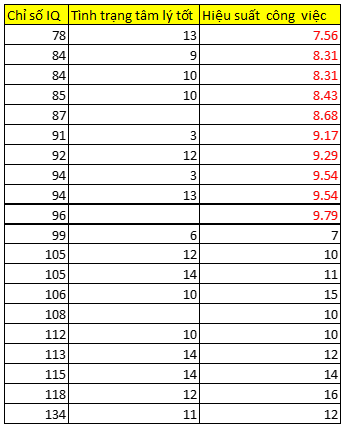
Nhìn lại bảng dữ liệu đầy đủ dưới đây không có missing, các bạn có thể thấy các giá trị impute vào ở trên chênh lệch khác nhiều so với bảng dữ liệu đầy đủ trong thực tế. Qua đây thấy được khi 2 biến không có mối quan hệ với nhau, thì regression imputation sẽ không đem lại hiệu quả. Nếu đây là một tập dữ liệu phức tạp hơn, có nhiều biến hơn thì chúng ta có thể chọn lựa các biến độc lập x phù hợp dựa trên ma trận hệ số tương quan để đánh giá mối quan hệ ban đầu giữa chúng với biến mục tiêu y (là biến có missing values)
Sau cùng nhìn vào biểu đồ dưới đây:
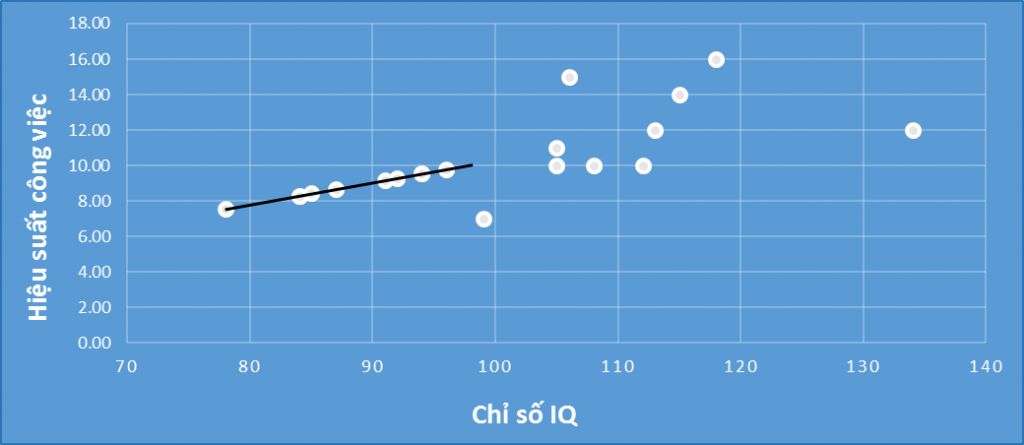
Các bạn có thể thấy các giá trị impute sau khi thêm vào tạo thành những điểm dữ liệu nằm trên một đường thẳng hướng lên. Như vậy khi mang tập dữ liệu mới đi phân tích correlation và regression khả năng sẽ cho ra hệ số tương quan R = 1, hệ số xác định R2 sẽ rất cao do lúc này chỉ số IQ và hiệu suất công việc có mối liên hệ thuận chiều một cách tuyệt đối.
Regression imputation là phương pháp được đánh giá tốt nhất so với các phương pháp còn lại đề cập trong bài viết này. Nhưng nếu tỷ lệ missing values là quá nhiều, hay các biến thực chất không có liên hệ gì với nhau, thì không thể áp dụng. Hơn nữa các giá trị dự báo từ phương trình hồi quy đều có sai số nhất định so với giá trị thực, sự chênh lệch này gọi là Residual, cho dù các biến có mối quan hệ tuyến tính bền vững.
Tuy nhiên vẫn có một phương pháp phân tích hồi quy khác áp dụng cho việc impute missing values tốt hơn, đó chính là Stochastic regression imputation. Phương pháp này như thế nào và hiệu quả ra sao chúng tôi sẽ trình bày ở bài viết tới, cách 1 tuần.
Như vậy chúng ta đã tìm hiểu các phương pháp đơn giản nhất trong imputation, xử lý dữ liệu missing. Chính vì tính đơn giản, không quá phức tạp nên chúng thường được áp dụng cho các trường hợp mising value đơn giản, không nghiêm trọng như dữ liệu có tỷ lệ missing values rất thấp, mục đích nghiên cứu, khảo sát dừng lại ở thống kê, cung cấp thông tin, không dùng để ra quyết định, không quan tâm đến ảnh hưởng của missing value, tập dữ liệu không có quá nhiều biến, và chỉ một vài biến có missing value,…
Ở những trường hợp khác với những gì chúng tôi vừa liệt kê, thì tuyệt đối không nên sử dụng Single imputation. Trong thực tế ngày nay, dữ liệu đã được nâng cấp lên rất nhiều về lượng, về dạng, về yêu cầu tốc độ xử lý, về tính phức tạp,…. Nên những kỹ thuật đơn giản trên hiện tại không được phổ biến như trước, mặc dù chúng vẫn còn đang được dùng trong lĩnh vực khoa học, xã hội cho các nghiên cứu, khảo sát.
Kết thúc bài viết về single imputation, hẹn gặp các bạn ở những bài viết tới.
Tài liệu tham khảo:
“Applied Missing Data Analysis: Methodology in the Social Sciences” của tác giả Craig K. Enders
“Missing data: a gentle introduction” của tác giả Patrick E. McKnight, Katherine M. McKnight, Souraya Sidani, Aurelio José Figueredo
“Handbook of statistical analysis and data mining applications” của tác giả Robert Nisbet, Gary Miner, Ken Yale
“A Review of Methods for Missing Data – Educational Research and Evaluation” của tác giả Therese D. Pigott
“Handbook of statistical data editing and imputation” của Ton de Waal, Jeroen Pannekoek, Sander Scholtus.
“Statistical Analysis with Missing Data” của tác giả Roderick J. A. Little, Donald B. Rubin
Về chúng tôi, công ty BigDataUni với chuyên môn và kinh nghiệm trong lĩnh vực khai thác dữ liệu sẵn sàng hỗ trợ các công ty đối tác trong việc xây dựng và quản lý hệ thống dữ liệu một cách hợp lý, tối ưu nhất để hỗ trợ cho việc phân tích, khai thác dữ liệu và đưa ra các giải pháp. Các dịch vụ của chúng tôi bao gồm “Tư vấn và xây dựng hệ thống dữ liệu”, “Khai thác dữ liệu dựa trên các mô hình thuật toán”, “Xây dựng các chiến lược phát triển thị trường, chiến lược cạnh tranh”.


 English
English